绝对值距离Steiner最小树问题的二进制粒子群算法

张娟敏，陈京荣，索孟鸽

(兰州交通大学 数理学院,甘肃 兰州730070)

Steiner树问题是指连接给定点的最小树长问题,其最优解称为Steiner最小树。绝对值距离Steiner最小树(Rectilinear Steiner Minimum Tree)问题是指两点之间的距离是绝对值距离,即连线只有水平和垂直两种形式,简称RSMT[1]。在线路铺设中往往涉及绝对值距离Steiner最小树。由于绝对值距离Steiner最小树问题已被证明是组合优化中的一个NP难题,因此,设计各种快速启发式算法以寻求问题的近似解,目前已经提出了许多智能解决方法,但基于二进制粒子群优化算法的研究成果却很少。

1961年,Melzak最先提出了Steiner树拓扑结构的解决方法[2];2006年,金慧敏等分别用蚁群算法和模拟退火算法求解欧式Steiner最小树[3];2008年,张瑾等应用改进的元胞蚂蚁算法研究了绝对值距离Steiner最小树[4];2014年,赵礼峰等提出了图的Steiner最小树问题的混合遗传算法[5];2016年,Kiefner提出了拓扑结构的绝对值距离Steiner最小树问题[6];2018年,Adrian等对单位平方内n个点的绝对值距离Steiner最小树进行了研究[1];然而借助二进制粒子群算法来求解绝对值距离Steiner最小生成树问题仍在持续研究中。

现给出用于求解绝对值距离Steiner最小树问题的二进制粒子群优化算法。首先对绝对值距离Steiner最小树问题和算法进行了详细的描述,利用二进制粒子群算法来编写程序,最后根据代入的数据得到了结果。

1 绝对值距离Steiner最小树问题

RSMT是指将平面上n个给定点集合P中任意两点P1=(x1,y1),P2=(x2,y2)间连线长度定义为绝对值距离(也称Manhattan距离)

Dist(P1,P2)=|x1-x2|+|y1-y2|。

RSMT的主要性质有：

性质1[7]设RSMT的原点数为n,则S点个数≤n-2。

性质2[7]RSMT问题是NP难问题。

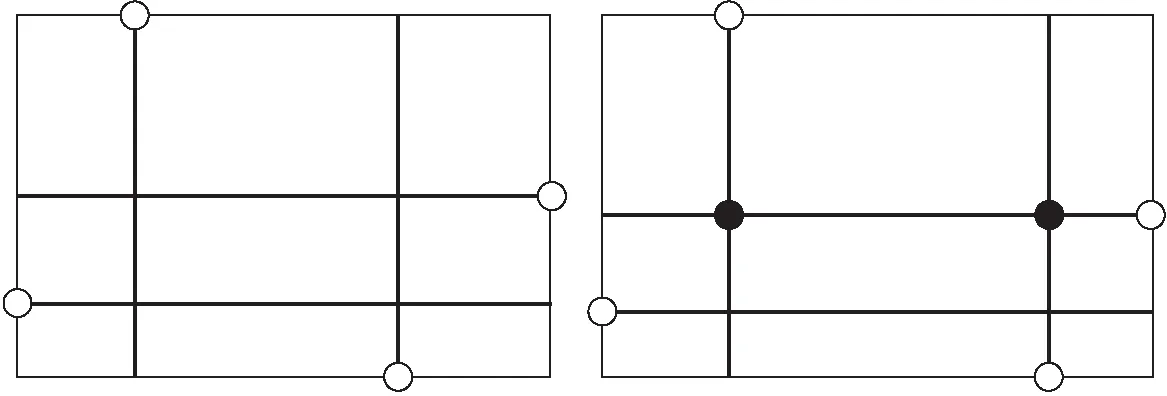
图1 Hanan定理示意图

性质3[8](Hanan定理) RSMT(T)上的Steiner点(S点)均在T经过的水平与竖直线的交点上(图1)。

求一个集合P的RSMT,可以通过各个端点分别引一条水平线和竖直线,由这些线的交叉点形成Hanan点集合,从Hanan点集合中按一定规则选取部分点作为Steiner点,用S表示,再求集合P与S构成的最小Steiner生成树。

2 离散二进制粒子群算法

基本粒子群算法可以很好地解决一些连续问题,但是针对离散的优化问题,文献[9]提出了离散二进制粒子群算法。

二进制粒子群算法便于表示本身具有二进制特性的问题,一个典型的例子是它可以用来表示神经网络的连接情况[10]。例如,1可以代表网络上两个节点相连,0可以代表两节点间无连接,因而一个二进制粒子群算法可以用来优化神经网络结构。二进制粒子群算法中,粒子在搜索空间的每个维度上的位置取值限制为0或1,但是对粒子的速度则没有此限制,粒子的速度主要用来决定粒子的位置取值为0或1的概率。如果粒子速度值较高,则粒子位置取值为1的可能性较大;如果粒子速度值较低,则粒子位置取值为0的可能性较大。文献[8]引入Sigmoid函数,通过对速度施加一个Sigmoid函数来获得一个[0,1]区间的值,其定义为

和基本的粒子群算法类似,二进制粒子群算法的速度更新

vij(t+1)=ωvij(t)+c1r1(pbestij(t))+c2r2(gbestj(t))。

(1)

但是与基本粒子群算法不同的是,在二进制粒子群算法中,位置的更新是采用一种具有概率性质的方式

(2)

其中,ω是惯性权重,r3j(t)是[0,1]内均匀分布的随机数,vij(t)是t时刻第i个粒子第j维的速度分量,xij(t)是t时刻第i个粒子第j维的位置,pbestij(t)为第i个粒子飞翔所经过的局部最优点,gbestj(t)为整个种群飞翔所经过的全局最优点,c1,c2是学习因子。

3 基于二进制粒子群算法的铺设网络线路

3.1 粒子的选择和编码

根据Steiner树的性质,若给定的原点数为n,则S点个数≤n-2。本文的粒子位置编码采用S点个数和S点坐标的实数编码方式[11],也就是粒子位置编码是由(n-2)个S点的坐标位置构成的。假设S点位置坐标的维数是二维,则每个粒子是由(n-2)个二维向量组成。由于粒子的速度和粒子的位置具有相同的数据结构,所以粒子的速度也是(n-2)个二维向量。

已知平面内n个点分别为P1=(x1,y1),P2=(x2,y2),…,Pn=(xn,yn),设

xu=max{x1,x2,…,xn}，xd=min{x1,x2,…,xn}，yu=max{y1,y2,…,yn}，yd=min{y1,y2,…,yn},

那么所有的S点都必定包含在点集{(x,y)|xd≤x≤xu,yd≤y≤yu}之内。

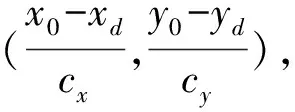
lx=[log2(10k×cx)]，ly[log2(10k×cy)][7],

每个待求点对应的二进制编码长度为L=lx+ly。每个个体最初都是随机生成一个二进制的字符串,其长度可以表示为ws=L×ds,其中ds是待求S点的个数。

3.2 适应度函数

假设原点集与S点集构成的完全图为G=(V,E,ω),其中V是点集,E是边集,ω是关联函数。给定任意的v1(x1,y1),v2(x2,y2)∈V,e12=(v1,v2)∈E,ω12=|x1-x2|+|y1-y2|,即绝对值距离Steiner最小树问题可以看作是在完全图G中寻找一个包含原点集与S点集的最小生成树ts,使得树的费用为各边的权值之和,即

(3)

3.3 粒子种群初始化过程

为了避免粒子分布集中,记录数据X维的最小值、最大值及Y维的最小值、最大值,并保证初始的粒子S点位置的随机性,本文将在最大值和最小值之间产生一个随机数。初始化粒子的速度都为0。

3.4 RSMT的离散二进制粒子群算法的实现

算法RSMT的离散二进制粒子群算法[12-13]步骤如下:

第1步 输入n个原点的坐标位置。

第2步 读入数据,确定S点的合理区域(区域由X维与Y维的最大值、最小值构成),在此区域内,按照S点的选取方法,找出所有的备选点(给定点所在水平竖直连线上的点),放缩这些点使得它在[0,1]区间上,粒子的初始速度为0。

第3步 用公式(3)计算每个粒子的适应度值,更新pbestij(t)、gbestj(t),判断全局最优是否达到预定最优值,若未达到,转第4步,否则,计算结束,输出全局最优粒子及S点的数目和位置坐标。

第4步 用公式(1)和公式(2)更新粒子的位置和速度。

第5步K=K+1,转第4步。

第6步 输出RSMT的值和S点的个数及位置坐标。

4 算法应用

此算例只考虑总路线长度最短的情况。已知有12个地点位于同一平面内,要在这些地方铺设网络宽带,使得费用最少。地点可以作为图G=(V,E)的一个顶点,即顶点集为V={P1,P2,…,P12},各地点的坐标如表1所示,边集E={PiPj,i=1,2,…,12,j=1,2,…,12,i≠j},各个地点之间的绝对值距离作为边的权。

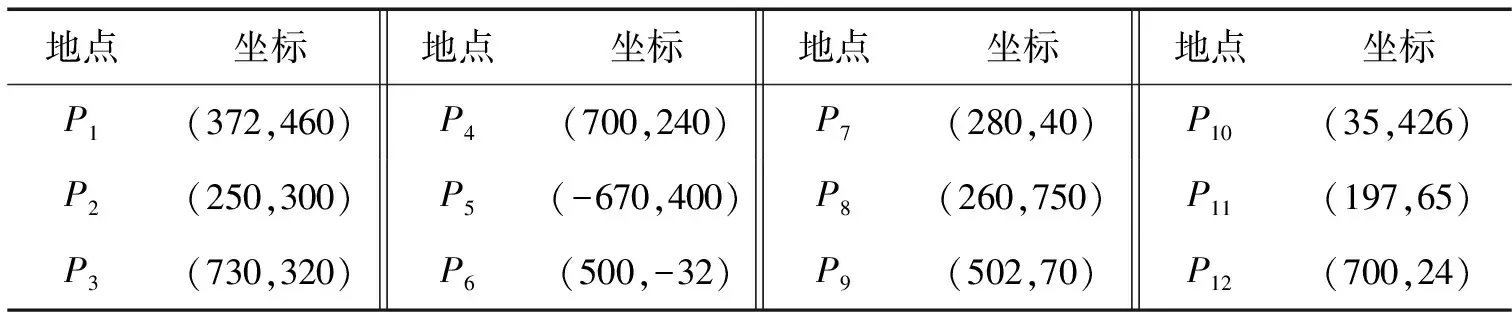
表1 各地点的坐标 m

费用最少就是这12个地点构成的连通图的最短路径问题,即绝对值距离Steiner最小生成树问题。

首先,在平面上画出这些点,将这些点控制在矩形区域内,搜索方法就是这个矩形区域内找Steiner点,减小搜索范围,提高计算效率,求解步骤如下：

第1步 输入已知点的坐标。

第2步 在平面内找到包含所有点在内的最小的矩形区域,将其作为搜索范围,对初始的数据进行处理。然后由S点的选取方法,找出备选点。

第3步 假设给定Steiner点的个数为3,随机产生规模,N=10,K=20,取ωmin=0.1,ωmax=0.6,c1=c2=2,vmax=2。

第4步 计算每个粒子的适应度值,更新pbestij(t)、gbestj(t)。

第5步 输出近似最小Steiner生成树的权值为2795,Steiner点为(260,426)、(260,65)、(700,65),如图2、图3所示。

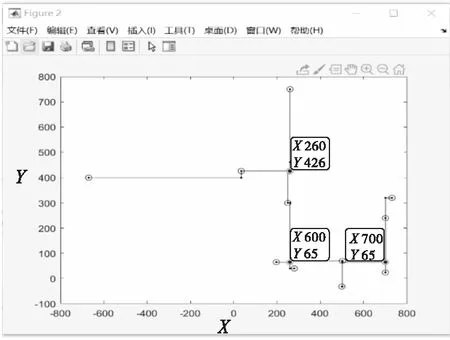
图2 绝对值距离Steiner最小树

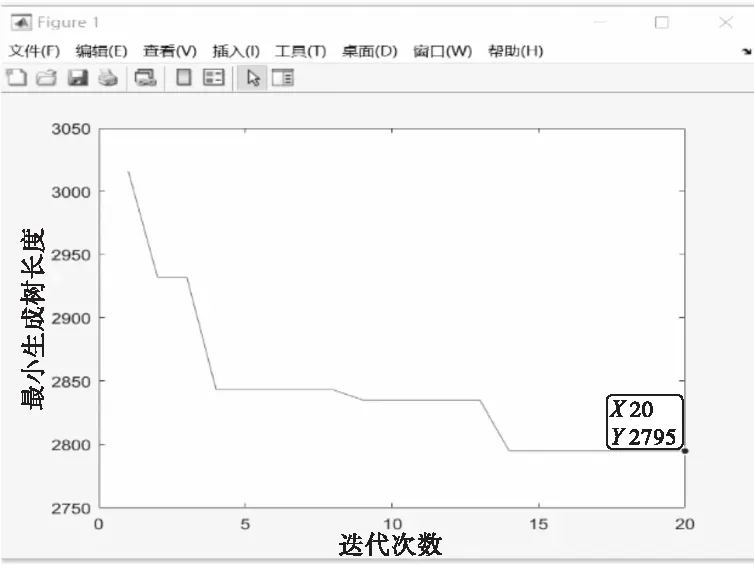
图3 迭代次数与最小生成树长度

图中的结果是利用MATLAB编程,在Windows10系统中运行得到的。对于给出的12个地点,经过多次试验得,当Steiner点为3时效果最佳,算法平均迭代20次左右后得到了绝对值距离Steiner最小树,还得到了Steiner点的坐标和最小Steiner生成树的图形。

5 结语

本文阐述了绝对值距离Steiner最小树问题和二进制粒子群算法,并将网络铺线问题转化为最小Steiner生成树的问题。最后利用二进制粒子群算法对最小Steiner生成树问题进行求解,获得了一组最优的斯坦纳点集,其和顶点构成的最小生成树为绝对值距离Steiner最小树的近似最优解,以该最小生成树作为整体结构的线缆即为最终优化后的方案。