基于遗传算法和破坏重组算法的外卖配送研究
2022-05-07唐传茵刘春龙
唐传茵 刘春龙
摘 要:文章针对有大量订单的外卖商家,解决外卖骑手高效配送外卖的问题,应用遗传算法和破坏重组算法对外卖配送路线进行分析;首先利用遗传算法对配送路线进行自然数编码,随后进行选择交叉变异操作,通过迭代优化得到次优配送路线,在遗传算法的基础上再与破坏重组算法结合,使配送路线图进一步优化;通过MATLAB工具,对外卖配送进行仿真,得到迭代优化图和配送方案路线图。通过对算法结合前后得到的配送路线性能指标的比较,验证遗传算法和破坏重组算法结合的优越性。
关键词:遗传算法;破坏重组算法;外卖配送;配送路线
中图分类号:F252.14 文献标识码:A
Abstract: In this paper, the delivery route is analyzed by genetic algorithm and destruction recombination algorithm to solve the problem of efficient delivery by delivery drivers for takeaway merchants with large quantities of orders. Firstly, genetic algorithm was used to encode the natural numbers of the distribution route, and then the selection crossover mutation operation was carried out to obtain the sub-optimal distribution route through iterative optimization. On the basis of genetic algorithm, combined with the destruction recombination algorithm, the distribution route was further optimized. Through MATLAB tools, the external distribution simulation, iteration optimization diagram and distribution scheme roadmap. By comparing the performance indexes of distribution routes before and after the combination of genetic algorithm and destruction recombination, the superiority of the combination of genetic algorithm and destruction recombination is verified.
Key words: genetic algorithm; destruction recombination algorithm; take-out delivery; delivery routes
0 引 言
在外卖平台系统的设置中,配送时间是最重要的指标,超时是不被允许的,一旦发生,骑手便有可能收到差评,这会导致他们收入降低,甚至淘汰。在外卖平台给生活带来极大便利的同时,外卖骑手的安全问题,如何合理规划配送路线,高效率完成配送任务是重要的研究课题。
外卖配送问题,实质上是带有时间窗的VRP问题,针对VRP问题和外卖配送问题,国内外学者们进行了大量的相关研究。文献[1]建立了一种改进型的单场站、多辆车车辆路径数学模型,将分枝界定法加以改进,设计出了一种车辆调度问题的精确算法,并对算法进行编程验证。文献[2]将可行解空间以恰当的方法分成一个个的子集,在对各可行解子集计算出目标下界的基础上,重复分支与定界操作,以求出最终目标;另一种求解VRP問题的方法是现代启发式优化算法,以自然仿真算法为主,其中对遗传算法的研究较多,文献[3-5]都是对研究的问题先建立VRP模型,然后利用改进的遗传算法从初始种群中找到最优解。还有一些学者利用其他的现代启发式优化算法解决VRP问题,文献[6]引入节约矩阵作为先验信息引导蚂蚁搜索,通过不同搜索时段采用不同的信息素挥发因子,使算法更好地在“探索”和“利用”之间达到平衡,并对较优解进行优化。文献[7]分析供应商,客户和码头三者组成的VRP问题,给出了该问题的一个混合整数非线性数学公式,提出了一种蚁群系统与模拟退火相结合的混合元启发式算法。文献[8]将解决VRP问题的思路应用到外卖配送中,分正常路况和拥堵路况两种情况,将利润最大、客户满意度最高和总里程最小作为优化目标函数,运用禁忌搜索算法进行求解。文献[9]从配送模式的角度出发,实现一个多起点启发式的规划路径来解决沃尔玛和亚马逊的“最后一英里”和“当天送达”问题。
本文从外卖骑手的角度出发,将遗传算法和破坏重组算法结合,得到最优配送路线,并通过MATLAB仿真验证。
1 配送路径规划分析
1.1 基本遗传算法的组成要素
1.1.1 染色体编码方法
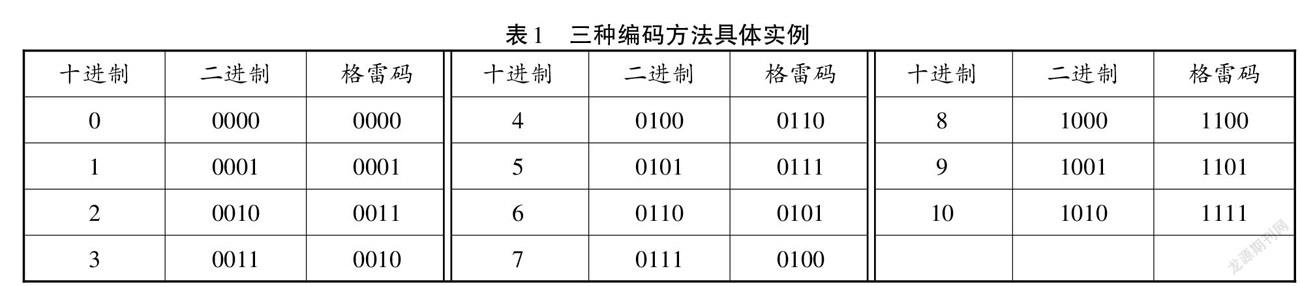
遗传算法的编码方法有自然数编码、二进制编码和格雷码编码等。
自然数编码中由“1”“2”…“n”组成,每一个基因位代表一个顾客,基因序列代表配送的顺序,由于需要多名配送人员对所有订单进行处理,所以用数字“0”将各个配送员的配送路线分开,以此表示多条配送路线。二进制编码由“1”“0”组成,较为简单,具有编码、解码操作简单易行,交叉、变异等遗传操作便于实现,符合最小字符集编码原则等优点,但是由于时间窗约束的限制,此外卖配送路径优化问题是基于次序的组合优化问题,且染色体二进制编码方式的基因位数目多、交叉与变异结果数值范围控制难度大、存在汉明悬崖(Hamming Cliff)现象等问题;格雷码方法连续两个整数所对应的编码值之间仅仅只有一个码位是不同的,如表1所示。
格雷码方法提高遗传算法的局部搜索能力;交叉变异易于实现等优点,结合本文研究问题,采用自然数编码方法。
1.1.2 适应度函数
通过染色体自然数的编码,可以保证骑手具有明确的行驶路线,但是不能保证解码的各条路径都满足载重量约束和时间窗约束,所以为了寻求最优值,引入惩罚函数对不符合约束的路径进行惩罚,惩罚函数如下式所示:
fs=cs+αqs+βws (1)
其中:cs是配送员行驶的距离,qs是各条路径违反容量约束之和,ws是各条路径违反时间窗约束之和。由于违反载重量约束相比违反时间窗约束情节较轻,因此α=10, β=100。
由于配送员的行驶距离,违反容量约束之和,违反时间窗约束之和单位不统一,因此需要对其进行数据归一化处理。本文拟用公式(3)对其进行数据归一化。
1.1.3 种群初始化
在初始化阶段,由于有最大载重量的约束,顾客数目一般远超最大载重量,因此配送路径的产生需要两个过程:初始化配送路径数目k=1,当第1条路径满足载重量要求时,则将遍历的顾客序号根据时间窗填到路径当中;如果第k条路径不满足载重量要求,则先储存前k条满足最大载重量约束的路径之后,更新k=k+1。
等所有顾客遍历完,将得到多条路径,将各路径之间用数字“0”收尾连接,得到一个包含所有顾客序号的染色体编号,这个染色体编号就是一个完整的配送方案。将种群个数设置为100,即会产生相应的100条染色体,至此,种群的初始化完成。
1.1.4 选择操作
通过轮盘赌法进行选择操作,轮盘赌法又叫比例选择算法,其基本思想就是适应度值越大,个体被选择的概率就越大。具体步骤如下:
步骤一:根据公式(4)计算出初始化后每个个体的适应度值。
步骤二:通过公式(5)计算出每个个体被遗传到下一代的概率。
i=1,2,3,…,n,n为种群数目。
步骤三:计算每个个体的累计概率如公式(6)所示:
1.1.5 交叉操作
对选择的父代进行交叉操作产生新的子代。
对染色体进行交叉操作如图1所示,首先确定基因交叉点,父代1的基因交叉点为3、4、5、6、7,父代2的基因交叉点为7、6、5、4、3,经过交叉操作得到图1(b)所示的子代染色体,子代染色体中含有重复的染色体,因此进行删除操作,最终得到图1(c)所示的子代染色体,从而完成交换染色体的操作。
1.1.6 变异操作
变异操作比较简单,随机选择父代的两个基因位置后交换,即可得到子代。
1.1.7 破坏重组算法
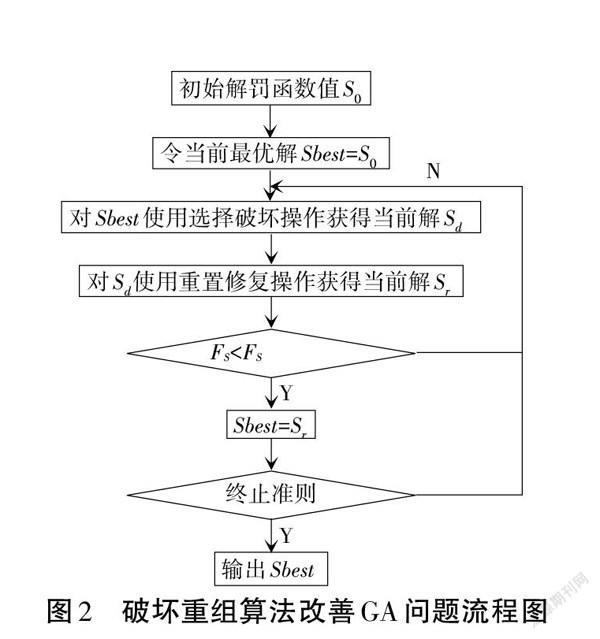
将遗传算法与破坏重组算法结合,用破坏重组算法进行进一步的完善。破坏重组算法的实质是通过交替的对基因位进行选择破坏和重置修复操作来改善初始解。
假设通过遗传算法得到的较优配送路线的罚函数值为S0,则用解决该类问题的流程图如图2所示。
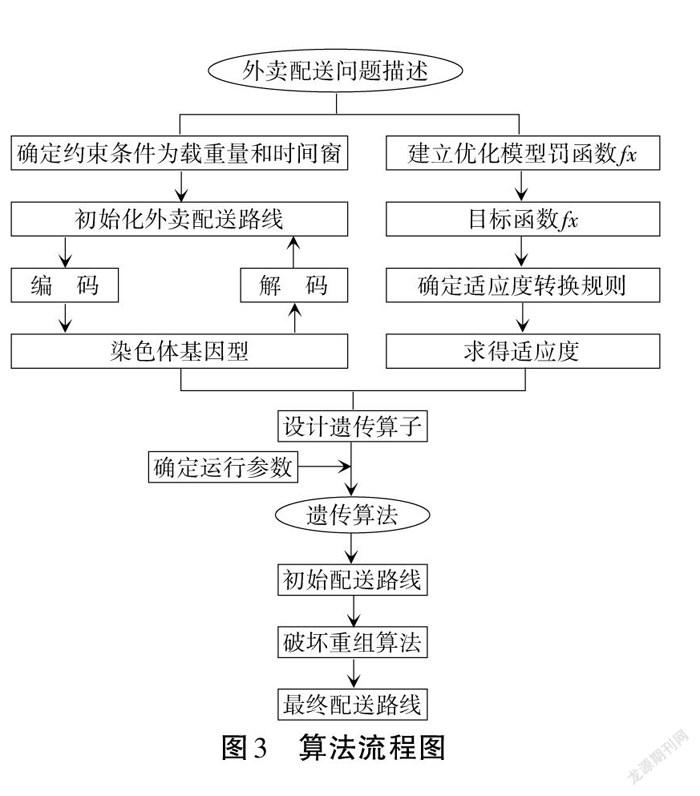
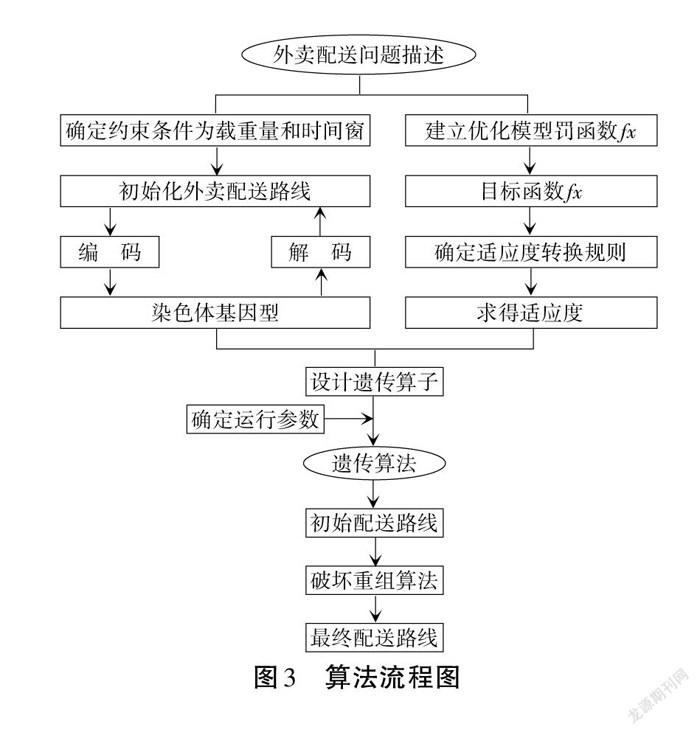
1.2 算法流程图
如图3所示为基于破坏重组算法,解决带载重量约束和时间窗约束的新型外卖配送模式。
2 仿 真
分別利用算法结合前后对110位下单顾客进行仿真,通过对仿真结果进行分析比较来验证遗传算法和破坏重组算法结合的优越性。
2.1 遗传算法仿真
当对110位下单顾客在传统配送模式下进行仿真时,只允许骑手到商家和顾客的次数为1,每个顾客和商家对应的配送时间窗在30~70分钟之间,时间窗从0开始,一直到遍历完所有的顾客和商家,服务时间为5分钟。
通过MATLAB工具对遗传算法进行仿真,得到如图4、图5所示的优化过程图和最优配送方案路线图。
得到的配送总距离为1 332.768米,配送结束时间为1 340分钟,违反载重量和时间窗约束的路线为0。
2.2 遗传算法和破坏重组算法结合的仿真
通过MATLAB对新型配送模式进行仿真,得到如图6、图7所示的优化过程图和最优配送方案路线图。
得到的配送总距离为828.8186米,结束配送时间为1 236分钟,违反载重量和时间窗约束的路线为0。配送路线为:
配送路线1:0→67→65→63→62→74→72→61→64→48→51→52→47→0
配送路线2:0→13→17→18→19→37→38→39→36→34→22→21→0
配送路线3:0→43→42→41→40→44→46→45→50→49→0
配送路线4:0→32→33→31→35→29→15→16→14→12→99→2→75→0
配送路线5:0→20→24→25→27→30→28→26→23→0
配送路线6:0→5→90→>87→86→83→82→84→85→88→89→91→0
配送路线7:0→3→7→8→10→11→9→0
配送路線8:0→98→96→95→94→92→93→97→100→6→4→1→0
配送路线9:0→81→78→76→71→70→73→77→79→80→0
配送路线10:0→57→55→54→53→56→58→60→59→68→66→69→0
得到违反约束的路径随着迭代次数变化图如图8所示:
得到违反顾客时间窗数目随着迭代次数变化图如图9所示:
3 仿真结果分析
3.1 优化过程图和最优配送方案路线图分析
首先对优化过程图进行分析,上图4和图6分别为种群数目100,迭代100次得到的遗传算法优化过程图和遗传算法与破坏重组算法结合的优化过程图。
在优化过程图中,横坐标表示迭代次数,纵坐标表示归一化后的罚函数值,罚函数值越小代表规划的路线越合理。由于开始的路线图是随机的,因此违反载重量和时间窗约束的路线较多,再加有权重的存在,所以开始的罚函数值较大。随着不断的优化,加之违反载重量和时间窗口的惩罚成本高,当迭代十几次之后,违反载重量和时间窗的路线变为0,只有骑手的行驶路程起作用,如图4和图6在迭代次数为10左右所示。随着迭代次数的再度增加,遗传算法与破坏重组算法结合的适应度函数的最优值也都慢慢收敛到0~1之间稳定不变,即表示已找到最优配送路线。
在图5遗传算法下得到的最优配送方案路线图中,横纵坐标分别代表顾客点地理位置的横纵坐标,每根颜色的折线代表不同骑手的配送路线,带序号的圆圈表示顾客的位置。
在遗传算法模式下得到的配送路线中,12条配送路线表示有12名配送员参与此次配送任务,以紫色配送路线为例,该骑手从接到订单任务后出发,依次给顾客序号90,87,81,78,76,71,70和73配送外卖,最后返回商家。
图7遗传算法与破坏重组算法结合模式下得到的最优配送方案路线图中。以配送路线1为例,该名骑手从商家出发,按照如下所示的配送路线0→67→65→63→62→74→72→61→64→48→51→52→47→0依次给顾客配送外卖,最后返回商家另外9条配送路线同理,另外该两种算法的结合减少了配送员数量的使用,更加降低了成本。
图8和图9反映了违反容量约束路径数目和违反时间窗数目随着迭代次数变化图。违反容量约束指的是每个配送员为了劳动强度要求,一次外出配送有最大载货量要求,超过这个数目是不被允许的,这是保障了骑手的劳动强度,从外卖骑手角度出发提出的要求;违反时间窗约束是指每个顾客点完外卖之后具有一定的时间窗要求,配送员需要在这个时间窗将外卖送到顾客手中,超过这个时间窗或者过早都是不被允许的,这是从顾客的角度出发提出的要求。迭代次数为0时,对应遗传算法初始化操作,通过图8和图9直观看到,随着迭代次数增加,违反容量约束数目和违反时间窗数目都在减小,并且最终收敛到0。
3.2 性能指标比较
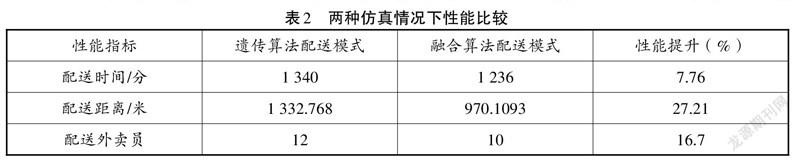
如表2所示为两种仿真情况下配送时间和配送距离性能的比较。
通过表2可以直观看到,遗传算法和破坏重组算法结合的模式相较于只运用遗传算法得到的配送路线,配送时间减少了7.76%,配送距离减少了27.21%,配送外卖员从12个减少到10个,因此整体效率更高,成本更低,表现出了很好的优越性。
4 总 结
通过联系社会热点,从外卖平台骑手的安全利益角度出发,兼顾企业的效率和顾客的时间保障,针对具有大量外卖订单的商家,将遗传算法和破坏重组算法结合,对外卖配送路线进行规划。
为了比较遗传算法和破坏重组算法求得的配送路线的优越性,本文分别对遗传算法和遗传算法与破坏重组算法结合的配送路线进行了编码,并且利用MATLAB平台进行仿真,并对得到的优化过程图和最优配送方案路线图做了分析与比较,通过比较可以直观地看到遗传算法和破坏重组算法结合求得的配送路线无论是在配送时间还是配送距离都有很明显的性能提升。
参考文献:
[1] 曹平方,李灵,李诗珍. 基于分枝界定的VRP模型精确算法研究及应用[J]. 包装工程,2014,35(17):97-101.
[2] Errico F, Desaulniers G, Gendreau M, et al. A priori optimization with recourse for the vehicle routing problem with hard time windows and stochastic service times[J]. European Journal of Operational Research, 2016,249(1):55-66.
[3] 周生伟,蒋同海,张荣辉. 改进遗传算法求解VRP问题[J]. 计算机仿真,2013,30(12):140-143,157.
[4] 范厚明,耿静,李阳,等. 模糊需求与时间窗的VRP及混合遗传算法求解[J]. 系统管理学报,2020(1):107-118.
[5] 冉崇善,张妍. 基于混合遗传算法的大规模VRP问题算法研究[J]. 电脑知识与技术,2016,12(18):182-184.
[6] 王晓东,张永强,薛红. 基于改进蚁群算法对VRP线路优化[J]. 吉林大学学报(信息科学版),2017,35(2):198-203.
[7] Moghadam S S, Ghomi S M T F, Karimi B. Vehicle Routing Scheduling Problem with Cross Docking and Split Deliveries[J]. Computers & Chemical Engineering, 2014,69:98-107.
[8] Allahyari S, Salari M, Vigo D. A Hybrid Metaheuristic Algorithm for the Multi-Depot Covering Tour Vehicle Routing Problem[J]. European Journal of Operational Research, 2015,242(3):756-768.
[9] Archetti C, Savelsbergh M, Speranza M G. The Vehicle Routing Problem with Occasional Drivers[J]. European Journal of Operational Research, 2016,254(2):472-480.
[10] 王荃菲. 快餐外賣配送路径方案研究[D]. 北京:北京交通大学(硕士学位论文),2017.
[11] Taha Yassen E, Ayob M, Ahmad Nazri M Z, et al. Meta-harmony search algorithm for the vehicle routing problem with time windows[J]. Information Sciences, 2015,325:140-158.
[12] H?觓, Bostel, Langevin, Rousseau, et al. An exact algorithm and a metaheuristic for the multi-vehicle covering tour problem with a constraint on the number of vertices[J]. European Journal of Operational Research, 2013,226:211-220.
[13] Karaoglan, Altiparmak, Kara, et al. The location-routing problem with simultaneous pickup and delivery[J]. Formulations and a heuristic approach Omega, 2012,40:465-477.
[14] Lopes, Souza, da Cunha, et al. A branch-and-price algorithm for the multi-vehicle covering tour problem[J]. Electronic Notes in Discrete Mathematics, 2013,44:61-66.
[15] Baldacci, Mingozzi, Roberti, et al. New route relaxation and pricing strategies for the vehicle routing problem[J]. Operations Research, 2011,59(5):1269-1283.
收稿日期:2021-12-20
基金项目:中央高校基本科研业务费项目(N2103028)
作者简介:唐传茵(1979-),女,辽宁沈阳人,东北大学机械工程与自动化学院,博士,硕士生导师,研究方向:群智能优化算法、自动驾驶、车辆动力学;刘春龙(1997-),男,山东临沂人,东北大学机械工程与自动化学院硕士研究生,研究方向:群智能优化算法、自动驾驶。
