基于DPC-SVDD的制造过程异常诊断
2022-05-06沈维蕾杨雪春吴善春
沈维蕾, 杨雪春, 吴善春
(合肥工业大学 机械工程学院,安徽 合肥 230009)
0 引 言
随着市场竞争压力的增加,制造业生产方式已逐渐向多品种、小批量模式转变,导致传统的统计分析方法难以有效控制小批量生产过程质量[1]。传统质量监控以及异常诊断方法通常假设采集的数据是连续的,并且遵循正态或多元正态分布,在此基础上才能建立较高精度的统计过程控制图来检测生产过程质量是否受控[2-4]。
近年来,有研究者开始将数据挖掘与统计过程控制相结合来控制非正态生产过程质量,并取得了很好的效果[5]。针对中小批量生产过程,文献[6]提出了一种结构化方法,将具有相似生产特征的生产过程进行聚类分析,用以获得足够的样本数据监控小批量生产过程,并成功地用于镗铣床的制造过程中;文献[7]提出一种基于共轭贝叶斯方法的多批次小批量生产的控制图,该方法首先从先前的批次中找出适当的先验信息,然后基于过程均值和过程方差的贝叶斯估计量,提出了用于计算控制极限的共轭贝叶斯方法;文献[8-9]使用支持向量机技术通过归一化的监控统计数据来构造鲁棒的K控制图,结果表明,除了非常规数据的灵活性外,强大的K图还可以有效地处理自相关过程数据;文献[10]根据支持向量数据描述 (support vector data description,SVDD) 算法提出了基于核距离的K控制图,K控制图的监测统计量根据观测点与SVDD算法生成决策边界之间的距离得到,并通过调节SVDD算法的参数调整控制限制;文献[11-12]研究了基于SVDD算法控制图控制限计算问题,在此基础上提出了基于核距离的D2控制图,该控制图根据多个统计量均值确定控制图的控制上限,因此不依赖于用户设置第一类错误和统计量分布类型;文献[13]提出了基于D2统计量的多元加权移动平均控制图S-EWMA,实验结果表明该控制图对小偏移较为敏感,且对于数据分布没有特定要求。
上述文献在解决质量过程异常监测时大多假设数据符合正态分布,但是当数据本身分布不均匀、分布较为分散时,通过SVDD算法训练得到的SVDD模型无法准确检测,导致漏报、虚警率增加。针对此问题,本文结合密度峰值聚类(density peaks clustering,DPC)与SVDD方法对小批量生产过程建立基于内核距离的DPC控制图,实现对小批量生产过程质量波动的实时监控,从而实现制造过程的多元质量监控与异常诊断。
1 SVDD算法及其缺陷分析
1.1 SVDD算法简介
SVDD是一种单分类数据描述算法,具有极强的模式识别能力和推广能力,因此被广泛应用于模式识别和异常检测领域[14-15]。该算法的核心思想是寻找一个能够包含全部或大部分目标类样本数据的最小超球体,同时使非目标类样本点位于超球体之外,而超球体的确定仅依靠目标集的训练样本。为了降低寻找超球体的难度,通常将训练样本数据映射到高维空间。若新样本点在高维特征空间的像落入超球体内部,则认为该样本属于目标类;反之,该样本点落入超球体外,则该样本点被识别为异常点[16]。SVDD分类结果如图1所示。
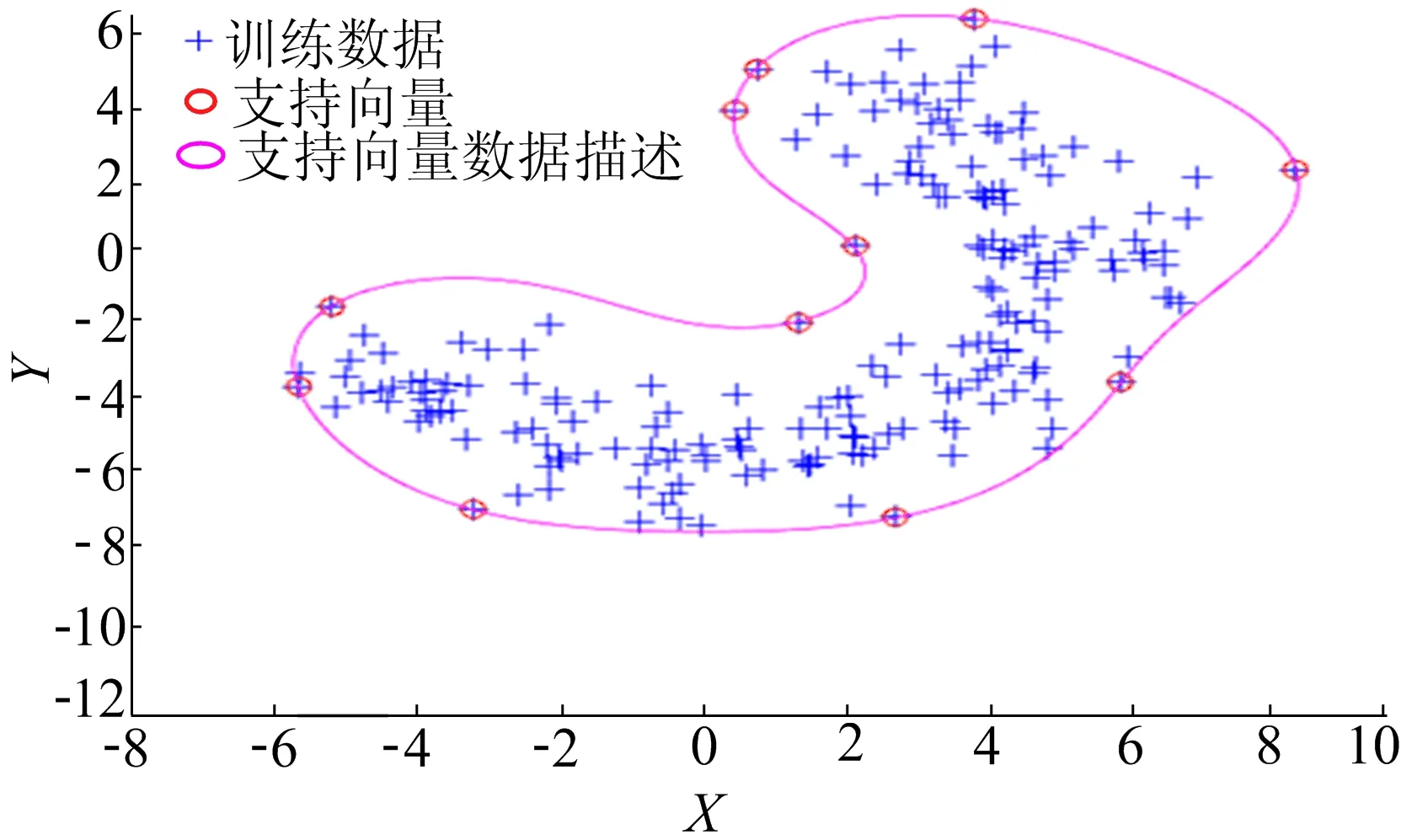
图1 SVDD分类示意图
假设需要对包含N个样本点的训练数据集进行描述,令{xi|xi∈X,i=1,2,…,N}为已知的训练数据集,超球体的球心和半径分别为A和R,则SVDD算法寻找的超球体应满足如下关系:
(1)
(2)
其中,xi·xj表示xi和xj的内积,可用核函数K(xi·xj)替换,考虑到核函数对分类器性能的影响,本文选择使用较为广泛的高斯核函数,即
(3)
通过求解二次规划问题可以得到最优解集α=(α1,α2,…,αn)。其中,存在少部分不为0的αi对应的变量xi使不等式中的等号成立,这些变量共同确定了分类器边界的支持向量。
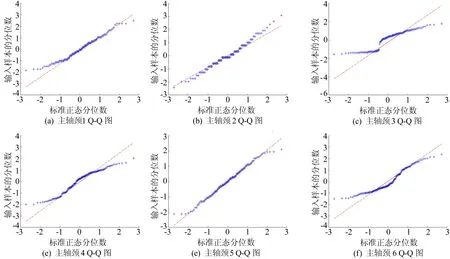
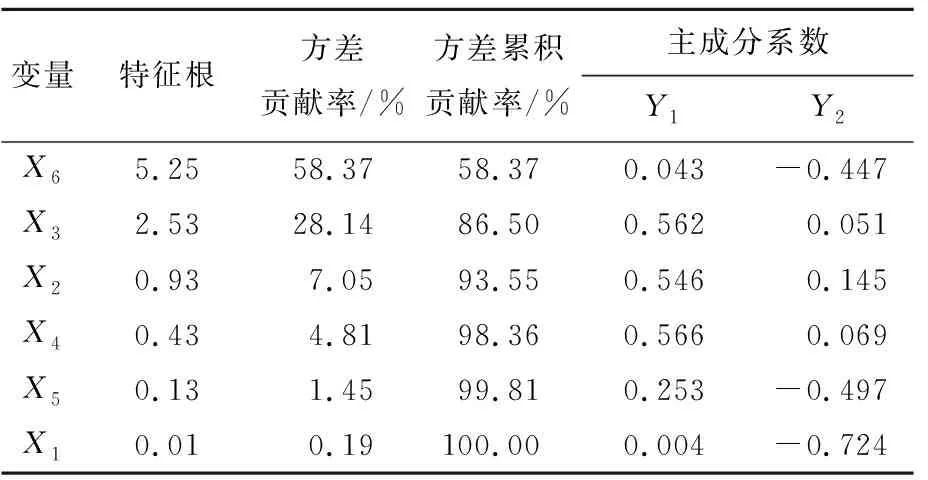
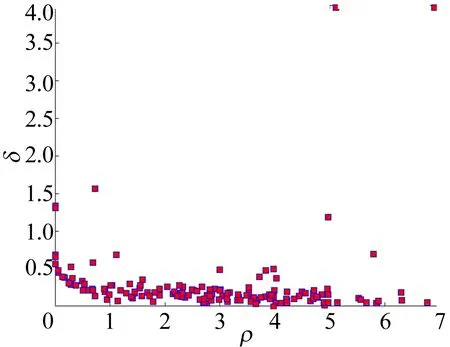
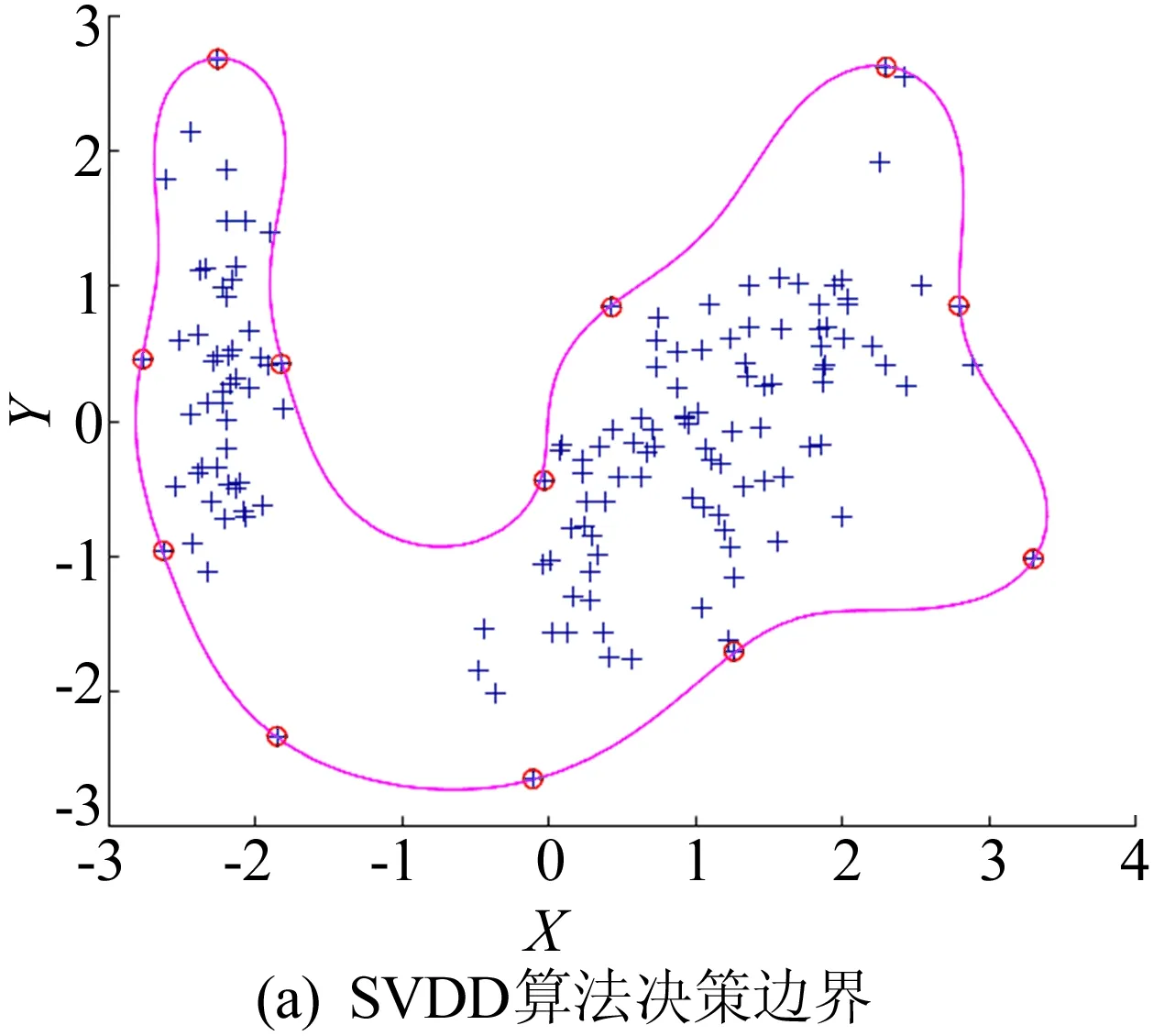
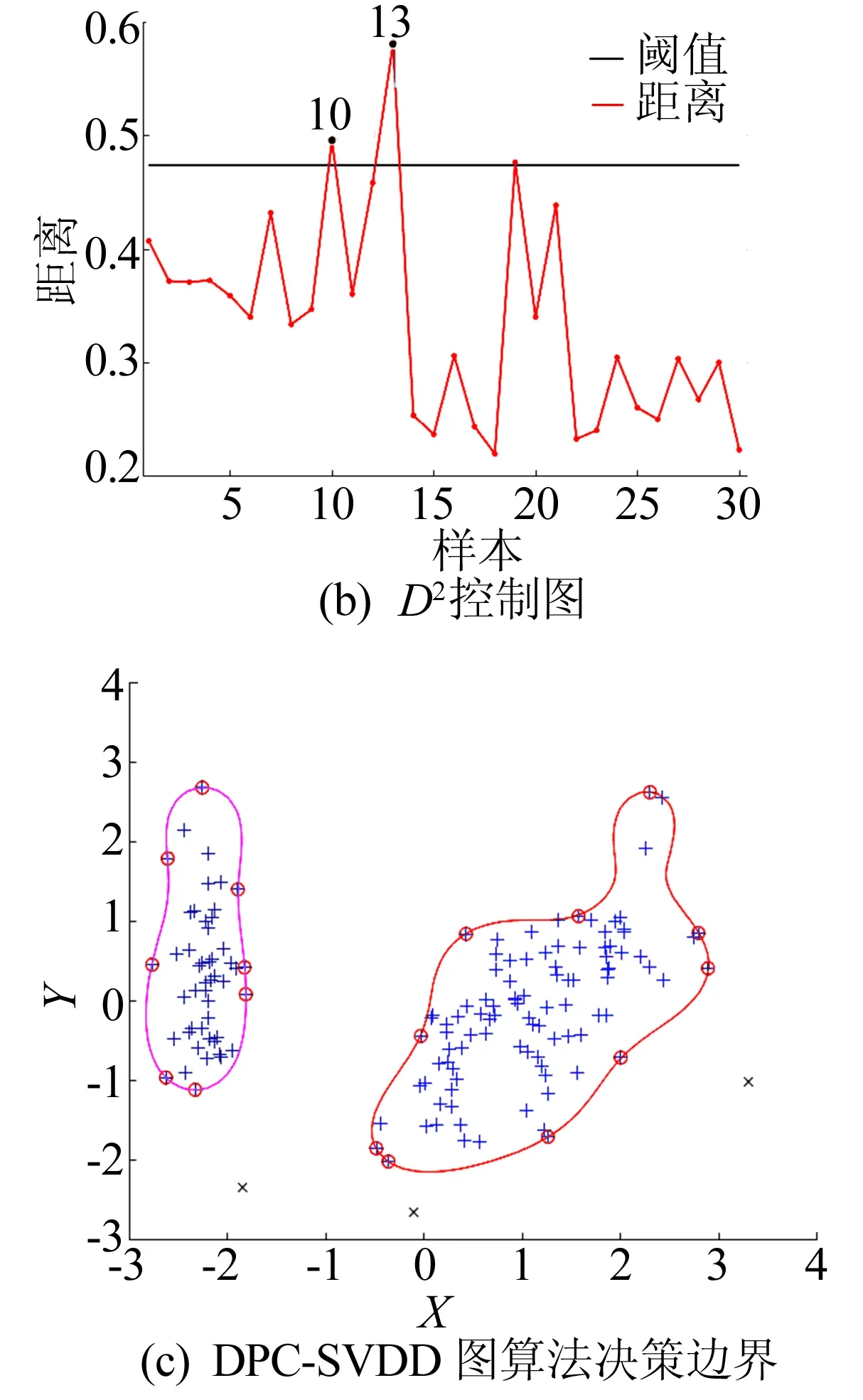
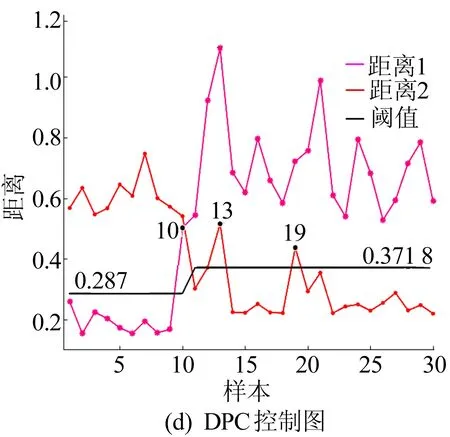
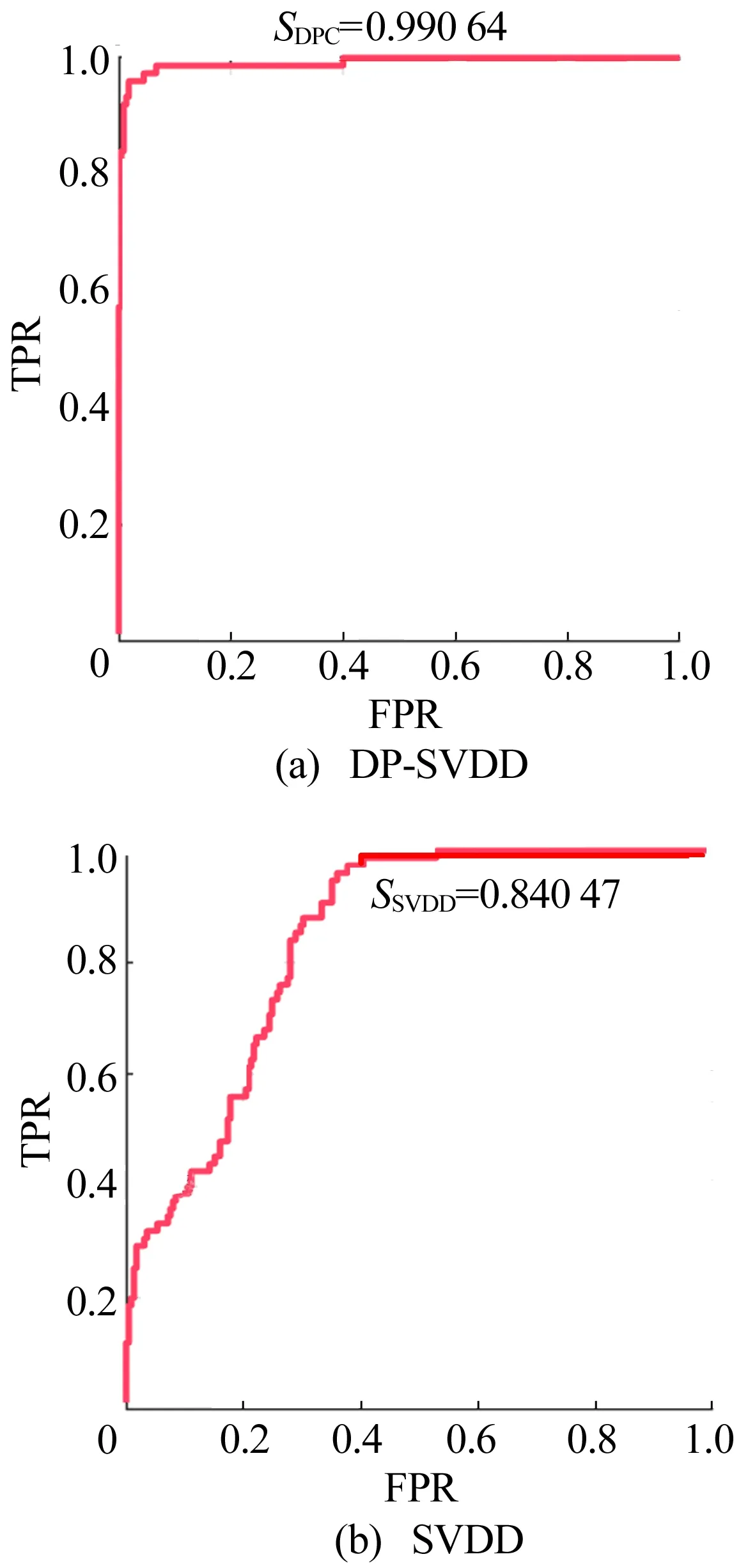
通过计算球体中心到权重因子小于C(0<αi R2=‖xk-α‖2=K(xk·xk)- (4) 为了判断测试数据z是否在超球体内部,可计算测试数据到球心A的距离D2。当测试点z到球心A的距离小于球体半径R时,测试点z位于球体内,即满足D2≤R2,则此样本点属于目标类,否则属于异常点。 距离D2的计算公式如下: (5) 此外,文献[17]定义了参数f,f=1/(NC),其中,N为目标类样本个数;C为控制超球体之外的目标类样本数的惩罚参数,通过调整f的大小可以达到控制超球体内部样本数的目的,适合的f有利于提高分类器性能。 SVDD算法属于典型的单分类算法,只能通过目标类数据对分类器进行训练,但是对于分布较为分散的样本数据,核函数的计算复杂度会导致SVDD训练难度增加。 此外,由于数据集各个区域的数据密度相差较大,原始的支持向量数据描述算法训练出的超球体体积较大,分散的决策边界导致非目标类样本点落入超球体内部的概率增加,最终引起分类器漏报率增加,降低模型的异常检测性能力。而且SVDD算法只能对目标数据集进行整体的边界描述,无法对数据集中所包含的多个不同样本之间的差异进行分析[17]。 不同参数下SVDD分类边界的分布情况如图2所示。 图2a所示为当数据本身分布不均匀时,训练得到的超球体体积较大导致无法对异常样本进行准确监测的情况。调整核函数参数以及惩罚参数后所得结果如图2b~图2f所示,出现将正常的目标类样本排除在超球体之外的情况,导致分类器虚警增加。 因此,在实际生产制造过程中,使用SVDD算法检测生产过程质量仍存在诸多限制。而本文提出的基于DPC改进的DPC-SVDD算法,可以有效解决上述缺陷,降低数据分布密度不均匀对SVDD分类器的消极影响。 为解决数据分布不均匀对SVDD分类的消极影响,本文采用基于样本分割的并行学习算法,提高算法效率。同时为了提高分类准确性,采用基于密度峰值的聚类算法DPC对SVDD算法进行改进,将训练样本集划分为K个高密度的子集,降低算法寻找超球体的难度。 DPC聚类算法的核心通过局部密度与相对距离这2个特征对聚类中心进行描述:① 每个聚类中心的局部密度高于周围所有的其他样本;② 聚类中心到其他密度较高点的相对距离较大。根据局部密度和相对距离这2个指标,该聚类过程可分为2步:第1步快速搜索密度峰值;第2步将密度峰标记为聚类中心,再将其余的点分配到各个簇中,最终得到若干个彼此之间相似度较低、密度较高的子集[18-19]。 DPC与传统密度聚类算法的不同之处在于该算法提出了从2个维度对聚类中心进行描述,即样本点的局部密度ρi、到局部密度比它大的样本点的距离δi。 假设存在数据集S={xi|xi∈X,i=1,2,…,N},dij=dis(xi,xj)表示样本点xi与xj之间的距离,对于S中的任何一点xi,都可以求出该点的局部密度ρi和相对距离δi,且这2个值仅取决于两点之间的距离dij。 任意一点i的局部密度ρi可以通过下式进行计算: (6)式中的dc为截断距离,是一个超参数,因此局部密度ρi可看作距离点i的距离小于dc的点的个数。 通过计算样本点i与其他具有更高密度的样本点之间的最小距离,计算相对距离δi,即 (8) 对于具有最高密度的点,其相对距离计算公式如下: (9) 最终可以得到所有点的局部密度ρi和相对距离δi,根据局部密度和相对距离得到基于ρ和δ的二维聚类决策图。根据决策图将具有最高局部密度和相对距离的样本点标记为聚类中心,最后将其他的样本点归入局部密度大于自身且距离最近的样本点所在的子类簇中,完成对所有样本点的聚类处理。 为解决小批量生产环境下生产过程数据分布不均匀的问题,本文将SVDD算法与聚类算法相结合,提出基于DPC-SVDD算法的质量诊断模型,模型整体框图如图3所示。 离线建模过程如下: (1) 数据预处理,将质量数据标准化后随机取样。 (2) 利用主成分分析法对采集到的生产过程特征数据进行主元分析计算各主元贡献度并提取其中贡献度较高的若干主元。 (3) 利用DPC算法对提取出的主元进行自动聚类分析,根据样本点的局部密度与相对距离得到决策图,最后依据决策图得到k个分布相对紧凑的子集。 (4) 训练SVDD模型建立k个超球体对样本空间进行划分。 (5) 依据各超球体决策边界和圆心建立K个控制图,根据(4)式计算控制限D2。 图3 DPC-SVDD质量监控模型 本节以某企业生产制造的再制造发动机曲轴生产过程为例来验证所提出方法的有效性。 某再制造企业生产的发动机曲轴有5个主轴颈,如图4所示。 图4 某再制造曲轴结构 该企业主要采用三坐标测量仪来测量主轴颈的圆度,该类型的测量仪精度为0.9 μm;对于曲轴的直线度,通常使用带千分表的专用测量平台进行测量,测量精度为1 μm。针对该企业连续生产的15个批次的曲轴,初步整理了各批次曲轴主轴颈圆度和直线度的检测数据总计150组,曲轴制造过程的部分数据见表1所列。 表1 再制造曲轴颈圆柱度和直线度数据 单位:μm 研究发现,该企业生产的再制造曲轴的径向跳动合格率较低,其合格率均值为85%,经分析影响曲轴径向跳动的主要因素为曲轴各主轴颈的圆度和曲轴的直线度。因此,本文以曲轴5个主轴颈的圆度和曲轴直线度作为监测指标,对再制造曲轴生产制造过程进行质量控制与优化。 在再制造过程中,废旧曲轴的数量与回收时间不确定,导致收集的数据可能不再符合多元正态分布。各主轴颈以及直线度的正态分布概率如图5所示。 由图5可知,曲轴各个变量均偏离正态分布,因此传统的质量控制方法使用受到限制。 图5 曲轴各变量正态分布性检验 为此,本文采用基于DPC-SVDD的质量控制方法进行再制造曲轴颈质量过程的监控。 (1) 利用主成分分析法进行数据降维,根据85%的方差贡献率确定主元数量。方差贡献率解释见表2所列。由表2可知,前2个主元包含了原始数据86.5%的分类信息。因此可以用主元Y1和Y2代替原始信息,主元Y1和Y2合成系数见表2所列。 (2) 利用DPC聚类算法对得到的二维特征数据进行聚类分析。使用DPC算法得到的二维决策图如图6所示。由图6可知,该二维数据可自动聚类为2个子类,聚类中心分别为二维决策图右上方2个点代表的数据;此外根据决策图可知,该数据集包含3个异常点,异常点距离正常样本较远且局部密度较大。因此,在训练SVDD超球体的过程中将导致超球体体积过大,在实际过程中增加漏报的概率。故将异常点放入测试样本集,用来测试分类器的识别率。 表2 方差贡献率解释 图6 二维决策图 原始SVDD算法和改进后的DPC-SVDD算法的运行结果如图7所示。其中:图7a和图7b为原始算法训练得到的超球体和相应的D2控制图;图7c和图7d为改进后的DPC-SVDD算法的训练结果。 由图7的对比结果可知:改进后的算法分类边界比较贴近质量受控数据集且具有更高的分类准确率,在测试的30组样本数据中存在3个质量异常点;而依据原始算法建立的控制仅对其中2个点(10、13)进行报错。 图7 SVDD算法改进前、后对比结果 对于偏移量较小的数据无法做出准确判断;在DP-SVDD算法下的DPC控制图通过综合比较样本点到2个圆心的距离可以准确判断出全部质量异常点,并及时发出警报,从而监测过程失控。 DP-SVDD和SVDD算法的性能比较结果如图8所示。其中:ROC曲线的横坐标表示假正类率(FPR);纵坐标表示真正类率(TPR)。 图8 DP-SVDD和SVDD算法的S比较 将模型的每个阈值(FPR,TPR)当作坐标画在坐标系中即可得到ROC曲线,该曲线下的面积用S表示,当S=1时,分类器接近完美。从图8可以看出,改进后的DP-SVDD算法SDPC=0.990 64,远大于SVDD算法的SSVDD=0.840 47。由此可以判断改进后的DP-SVDD算法对于质量异常波动的监测能力远高于传统的SVDD算法,在实际的质量过程异常监控中有着积极的意义。 针对生产过程中由于过程数据分布类型未知引起的传统质量控制图异常检测精度低的问题,本文提出结合SVDD和DPC的生产过程质量异常检测方法。首先,利用主成分分析法对质量特征数据进行特征提取、融合,降低算法的计算量、提高分类准确率;其次,采用DPC方法根据样本点局部密度和相对距离对样本数据进行自动聚类,相较于传统聚类,本文聚类算法不需要人为确定聚类数量,同时可以识别出噪点,保留质量受控数据,有利于提高算法准确率;然后,利用聚类得到的子集训练出相应的SVDD模型,根据超球体圆心A和半径R2建立DPC控制图监测生产过程;最后,将本文提出的DPC-SVDD方法与SVDD方法应用到再制造曲轴质量监测中,对本文方法的有效性和优越性进行比较,结果表明DPC-SVDD方法可以有效识别制造过程质量异常,并且识别速度较快、对质量偏移较为敏感。1.2 SVDD缺陷分析
2 改进的DPC-SVDD算法
2.1 DPC算法简介
2.2 DPC-SVDD算法过程质量监控模型


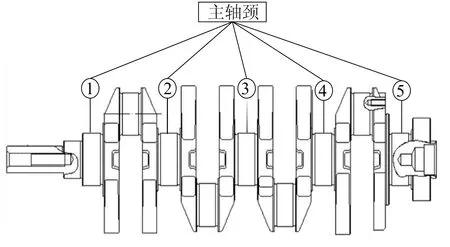
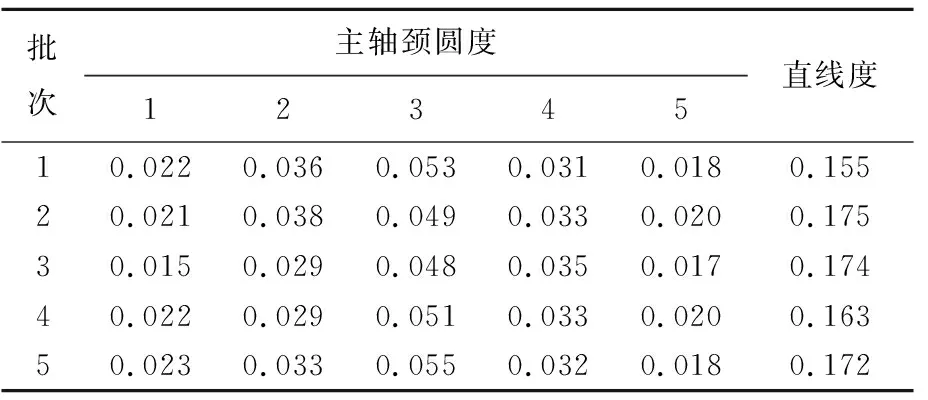
3 实例分析
4 结 论
