磁耦合Mn2+-Mn2+离子对发光行为研究进展
2022-05-06朱兴路宋恩海邹炳锁
朱兴路, 宋恩海, 邹炳锁, 叶 柿*
(1. 华南理工大学 材料科学与工程学院, 发光材料与器件国家重点实验室, 广东省光纤激光材料与应用技术重点实验室, 广东 广州 510641;2. 广西大学 资源环境与材料学院, 广西有色金属及特色材料加工重点实验室, 广西 南宁 530004)
1 引 言
Mn2+离子具有5个未成对的d电子,在5个3d轨道中具有252种填充方式并产生16个光谱项:6S、4P、4D、4F、4G、2S、2P、2D(1)、2D(2)、2D(3)、2F(1)、2F(2)、2G(1)、2G(2)、2H、2I[1]。在晶体场作用下,这些光谱项发生能级劈裂,其行为可以用Tanabe-Sugano(TS)图来描述。Mn2+的发光归属于4T1→6A1辐射跃迁,属于宇称和自旋双重禁阻跃迁,因此其荧光寿命通常在几毫秒~几十毫秒量级[2]。Mn2+的激发态能级较多且能隙较小,处于高激发态的d电子通常会弛豫到最低激发态能级,因此处于晶体单格位的Mn2+发光光谱通常是单峰。此外,由于Mn2+的3d电子裸露在最外层,其发光容易受到晶体场环境的影响,通过调节化学配位环境可实现绿光到红光的发射[2-3]。这些独特的发光性质使Mn2+成为发光材料领域重要的激活剂离子。商用发光材料中含Mn2+的材料有白光卤粉Ca5(PO4)3Cl∶Sb3+,Mn2+、绿粉Zn2SiO4∶Mn2+、BaAl12O19∶Mn2+和BaMgAl10O17∶Eu2+,Mn2+等。在近紫外激发的荧光材料转换的白光LED器件中,以Mn2+离子为红光发射中心的Eu2+或Ce3+共激活的荧光材料是具有应用潜力的红光材料,如Ba3MgSi2O8∶Eu2+,Mn2+[4]、SrZn2(PO4)2∶Eu2+,Mn2+[5]、M3MgSiO8(M=Ca,Sr,Ba)∶ Eu2+,Mn2+[6]、Ba2Ca(B3O6)2∶Eu2+,Mn2+[7]、Ca5(PO4)3Cl∶Eu2+,Mn2+[8]等。但Mn2 +的4T1→6A1宇称-自旋双重禁阻跃迁的特性导致其荧光寿命较长,使得材料在光子激发密度大的情况下容易达到光效饱和,进而影响器件性能的提升[8-10]。
在Mn2+掺杂体系中,研究发现,随着掺杂浓度的提高会出现一些不寻常的发光现象,例如单格位多峰发射、近红外发光、微秒量级的荧光寿命以及磁光效应减弱等[11-16]。研究者把这些现象主要归因于Mn2+-Mn2+之间的磁相互作用。铁磁(FM)材料和反铁磁(AFM)材料内部离子磁矩有序排列(其中前者平行排列,后者反向平行排列)的原因是材料内部存在附加磁场(又称分子场)。分子场来源于相邻原子或离子间发生的交换作用[17-20]。在FM材料中分子场场强可以高达107Gs,如此强的内磁场使材料内部磁矩自发平行排列;AFM或亚铁磁材料(FIM)中的分子场主要来源于两过渡金属离子间通过所键连的中间阴离子产生的超交换作用,在这种相互作用下离子磁矩反向平行排列。尽管AFM和FIM材料中的分子场场强相比于FM材料大大减小,但仍然对材料的物理性质如发光有重要的影响[17,20]。
目前,人们对Mn2+-Mn2+离子之间的磁相互作用与其发光机理的认识仍然不足甚至存在相互矛盾的地方,特别是后者夹杂着材料基质声子耦合、浓度猝灭等因素的干扰。本文综述了Mn2+-Mn2+离子对磁相互作用对其吸收光谱、发射光谱、荧光寿命以及磁光现象的影响及其研究进展,特别介绍引入光磁测量技术来推测在有/无光照条件下Mn2+自旋组态的变化来阐释磁相互作用下的发光行为。最后进行总结并展望。
2 磁耦合离子对与发光相关理论简介
Mn2+与最近邻Mn2+之间无论以FM还是AFM方式发生相互作用,当体系的热能(温度)升高到足以克服离子间的交换作用时,有序排列的磁矩被破坏,导致材料磁性变为顺磁性。图1(a)给出了发生AFM、FM有序转变的典型的磁化率-温度曲线。尽管在磁有序温度以上体系表现出顺磁行为,即磁无序,但仍然会存在着AFM或FM相互作用。研究表明,在高于居里温度(TC)/奈尔温度(TN)时存在Mn2+-Mn2+磁相互作用的体系,发光性质与没有磁相互作用的顺磁性材料不同。可用示意图对此进行说明,如图1(a)(ⅰ)所示,当Mn2+通过中间的配体离子与相邻Mn2+发生AFM相互作用时,在TN温度以下相邻Mn2+的磁矩反向平行有序排列;当温度超过TN时,相邻两Mn2+离子间仍然存在AFM相互作用(如绿色虚线框所示),只是宏观上磁矩无序排列。同理,FM体系的有序磁矩在TC以上时体现顺磁性,但两Mn2+离子间仍然存在FM相互作用(如绿色虚线框所示,如图1(a)(ⅲ))。而Mn2+以孤立形式存在时它们之间没有磁相互作用,Mn2+的磁矩排列杂乱无章,属于顺磁性(PM,如图1(a)(ⅱ))。
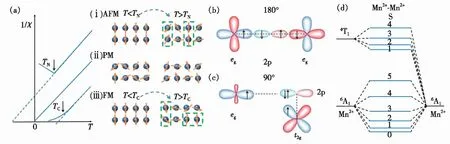
图1 (a)Mn2+- Mn2+离子间发生AFM相互作用(ⅰ)、无长程磁相互作用(ⅱ)、FM相互作用(ⅲ)时在TN/TC温度前后Mn2+磁矩的排列示意图;Mn2+-X-Mn2+超交换作用(X为配体离子)构型示意图:(b)180°,(c)90°;(d)Mn2+-Mn2+离子对电子能级的∣6A16A1>和∣6A14T1>。
掺杂在固体中的两个Mn离子处于最近邻阳离子格位时(相距约0.5 nm),根据所形成的Mn2+-Mn2+离子对的耦合几何构型,典型的超交换相互作用结构有两种[17]:180°和90°(如图1(b)~(c))。研究表明,过渡金属离子间的超交换作用强度与构型有关,当联接构型为180°时,离子间电子云重叠程度最大,超交换作用强度较强;反之,90°超交换作用弱[21]。此外,超交换作用强度随离子间距离的增加而减小,当两个相邻的过渡金属离子间距大于0.5 nm时,超交换作用强度急剧下降。
Vink等[22]曾提出Mn2+-Mn2+通过超交换作用可形成新发光中心,两个Mn2+离子分别以A和B表示,它们之间的自旋相互作用通过海森堡哈密顿量HAB进行描述[23]:
HAB=-2J(SASB),
(1)
其中SA和SB分别表示过渡金属离子A和B的自旋量子数,J表示交换耦合参数,该离子对的能级能量E(S)取决于HAB并通过下式表示:
E(S)=
-J[S(S+1)-SA(SA+1)-SB(SB+1)],
(2)
其中S为离子对总自旋量子数。离子间磁相互作用的类型可以通过J来进行判断。当J>0时,离子间发生FM相互作用;当J< 0时,离子间发生AFM相互作用。在单个Mn2+离子中,基态能级为6A1(S=5/2),最低激发态能级为4T1(S=3/2),电子在它们之间的跃迁为自旋禁阻跃迁(ΔS=1)。当Mn2+与邻近的Mn2+通过交换作用形成Mn2+-Mn2+离子对时,其基态SA=SB=5/2,从而S有5个分量,即5,4,3,2,1,0。当离子对吸收一个光子后,其中一个离子处于4T1能级,另一个离子处于6A1,则S分量有4,3,2,1。由此可以得到Mn2+-Mn2+离子对从∣6A14T1>到∣6A16A1>跃迁的各个可能的能级(如图1(d)所示)。从图1(d)可知,有些跃迁是ΔS=0的自旋允许跃迁。因此,Mn2+-Mn2+离子对的磁相互作用可以改变电子的自旋组态,打破孤立Mn2+的d-d跃迁自旋禁阻选律,进而影响Mn2+-Mn2+离子对的发光寿命。
3 Mn2+-Mn2+离子对发光行为及其研究进展
3.1 吸收光谱
在一些Mn2+高掺杂浓度的体系中,其吸收光谱在低温下出现精细结构,如McClure[24]在研究Mn2+掺杂的ZnS吸收光谱时发现470 nm和510 nm两个吸收峰在4.2 K下出现劈裂(如图2所示)。他认为该吸收峰的劈裂可能与Mn2+-Mn2+相互作用有关。为证明这一点,McClure通过这些峰劈裂能量计算Mn2+-Mn2+离子对能级的交换耦合常数,结果表明J=-9 cm-1。该数值与β-MnS变温磁化率拟合的耦合常数J=-8.7 cm-1相近,说明在该ZnS体系中Mn2+倾向于聚集且Mn2+-Mn2+间有AFM相互作用。根据这些吸收峰劈裂的拟合结果,McClure进一步提出这些精细结构是Mn2+-Mn2+离子对能级在四面体场下发生劈裂所导致的。此外,McClure还发现离子对的磁相互作用可以极大地影响Mn2+吸收光谱的强度。由于孤立的Mn2+在光激励下的电子跃迁是双重禁阻跃迁(自旋和宇称),其吸收光谱强度通常比较弱,但在一些高Mn2+掺杂浓度的体系中可以观测到强的(4Eg,4A1g)吸收峰,比低浓度Mn2+掺杂体系的吸收光谱强度大一个数量级左右[24]。该现象可归因于Mn2+与相邻Mn2+发生磁相互作用,其导致Mn2+禁阻跃迁的自旋选律部分解禁[24-25]。Ferguson等[26-27]通过监测KMnF3和不同Mn2+掺杂浓度的KZnF3变温吸收光谱,研究Mn2+离子由孤立到聚集形成离子对的吸收光谱变化。尽管高Mn2+掺杂浓度的KZnF3与低浓度掺杂的样品有相似的吸收光谱形状,但前者在(4Eg,4A1g)能级及其附近能级对应的吸收峰强度要远大于后者的强度。作者认为这种异于孤立Mn2+吸收光谱的行为是由Mn2+间聚集形成Mn2+-Mn2+离子对并发生磁相互作用部分打破了Mn2+自旋禁阻跃迁的限制导致的。此外,作者还研究发现KMnF3对应吸收峰的振子强度高达9.5×10-7,强于单个Mn2+的吸收峰振子强度(<1.7×10-8)。
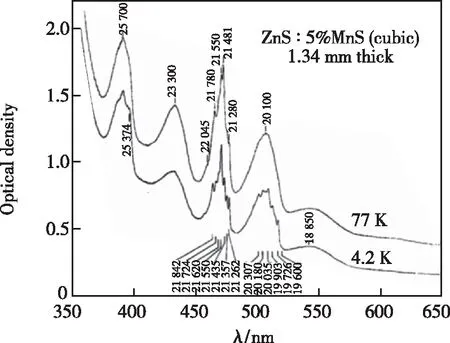
图2 ZnS∶5%MnS (cubic)在4.2 K和77 K下的吸收光谱[24]
3.2 发射光谱
Mn2+-Mn2+磁相互作用会导致原孤立的Mn2+发射峰位移动。通常,随着温度升高材料的晶格会膨胀,导致晶体场场强减弱。根据TS图,六配位的Mn2+从4T1到6A1的跃迁能量随晶体场强度减小而增加,Mn2+的发射峰向高能量方向移动(蓝移)[28-31]。因此,随温度升高发射峰发生红移的现象就可能与Mn2+-Mn2+间的相互作用有关,很早之前就有相关报道[22]。最近的研究如Orive等[32]在Mn2(HPO3)F2体系中,发现在10~150 K温度范围内Mn2+的发射峰随温度升高而红移(如图3(a)所示),这与前述的晶体场理论不符。Zhang等[33]在研究CaZnOS∶Mn2+体系时用Mn2+-Mn2+离子对的相互作用来解释随着Mn2+浓度增加其发射峰红移的现象。如图3(b)所示,当Mn2+掺杂浓度由0.005提高到0.1时,其发射峰出现了~8 nm的红移,由橙黄光变为红光。作者认为在高掺杂浓度下Mn2+-Mn2+离子对的浓度增加且晶胞体积变大,Mn2+-Mn2+间相互作用减小4T1与6A1能级间的能隙,表现为光谱红移。但由于Mn2+的吸收峰与发射峰存在部分重叠,其自吸收也可导致发光峰随浓度增大而红移。此外,如果Mn2+离子掺杂造成晶格收缩也可能导致光谱红移。因此,研究磁耦合Mn2+-Mn2+离子对发光的变化或者规律需要排除自吸收、掺杂引起晶格膨胀/收缩对光谱移动的影响。
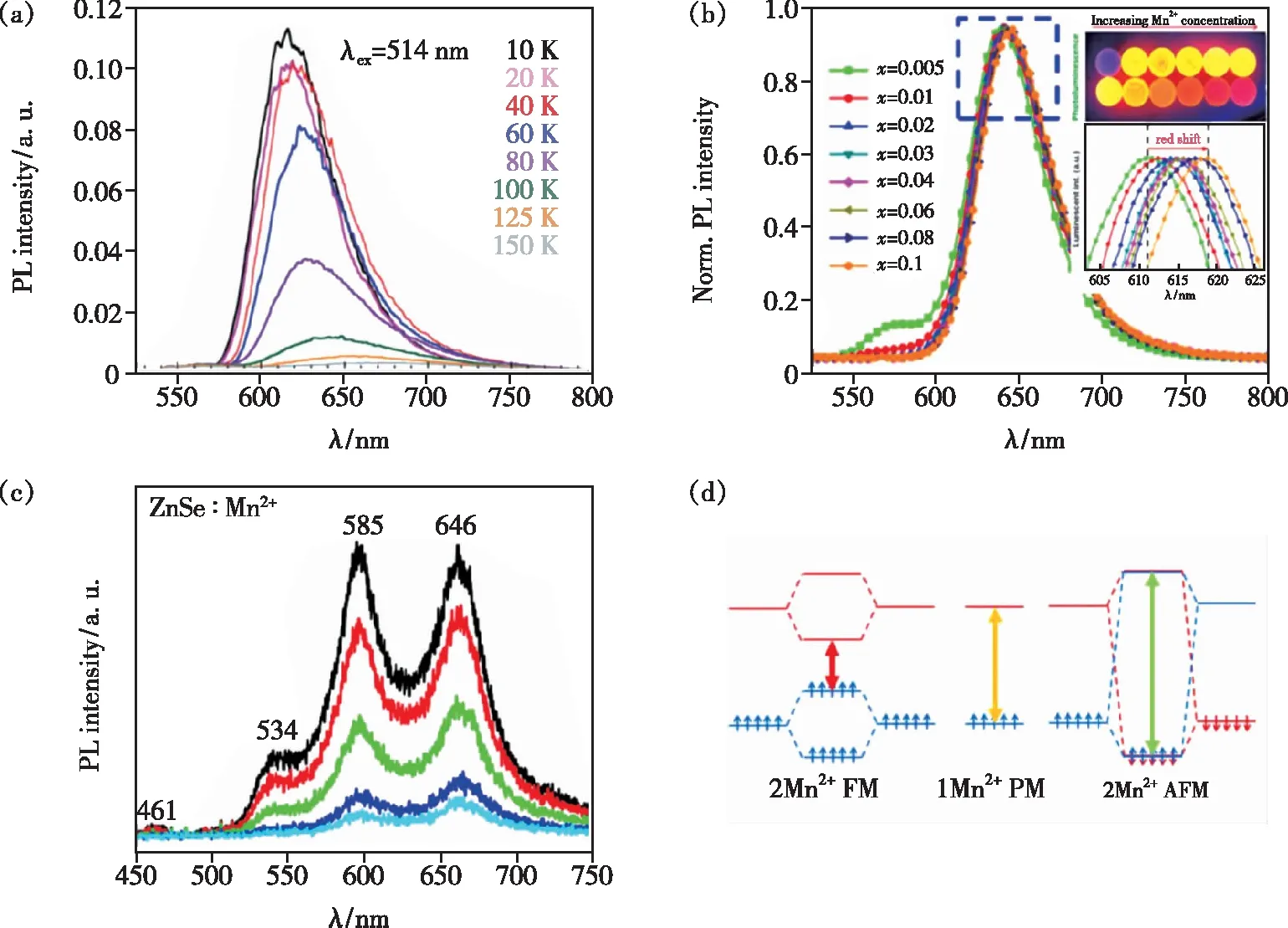
图3 (a)Mn2(HPO3)F2在514 nm激发下的变温发射光谱[32];(b)CaZn1-xOS∶xMn2+(x=0.005~0.1)的发射光谱[33];(c)ZnSe∶Mn2+在405 nm激发下的室温发射光谱;(d)顺磁性单Mn2+离子、Mn2+- Mn2+离子对分别以铁磁和反铁磁耦合时的发光跃迁示意图[47]。
Mn2+的多峰发射也是研究焦点。1967年,Gumlich等[34]在研究ZnS∶Mn2+体系时,发现室温下只有一个位于~590 nm的发射峰;当温度降到140 K以下时,出现了两个分别位于635 nm和745 nm的发光峰。作者认为这种Mn2+的多峰发射是由Mn2+-Mn2+离子间的磁相互作用导致。Goede等[35]也发现室温下ZnS∶Mn体系中Mn2+的浓度达到32%时会在原黄光发射峰附近出现一个能量更低的红光发射峰,且这两个发射峰具有相似的激发光谱。研究者们还在其他Mn2+掺杂体系中观测到Mn2+的多峰发射,如Mn2+掺杂的CdS纳米晶[36]、ZnS纳米颗粒[37]、ZnSe量子点[38]、CdS纳米线[39-40]和ZnSe纳米带[41]、KZnF3[42]、KMgF3[11]、CaO[43]、AMnX3(A=NH4,Rb,K;X=F,Cl)[44]等以及BaMnF4[45]和RbMnCl4[46],并认为这些发射峰是由Mn2+-Mn2+磁相互作用导致的,即磁耦合的Mn2+-Mn2+离子对可以形成一个新的发光中心。但这些峰的归属指认则有争议。例如在Mn2+掺杂的ZnSe纳米带中观测到461,534,585,646 nm的发射峰(如图3(c)所示)[47],Hou等认为其中461 nm的发射峰来源于ZnSe激子复合,585 nm发射峰是孤立Mn2+的发光,而534 nm和646 nm发射峰则与Mn2+-Mn2+磁相互作用有关。为了进一步地指认,作者用密度泛函理论计算(DFT)分别计算了以AFM和FM耦合的Mn2+-Mn2+离子对的d轨道能带间的能级差ΔE(d-d),结果表明AFM耦合的ΔE(d-d)=2.71 eV(571 nm),FM耦合的ΔE(d-d)=1.73 eV(717 nm)。作者认为,当两个Mn2+离子以FM耦合时,两个Mn2+离子的电子自旋平行分别占据成键轨道和反键轨道(能级),导致电子从最低激发态跃迁到基态(图3(d)最左边示意图的红色箭头)的能量减少;而以AFM耦合时,电子自旋反平行占据在反键轨道(能级)上,造成最低激发态到基态(图3(d)最右边示意图的绿色箭头)的能量间隙增大;这是以AFM/FM耦合的Mn2+离子对发光峰相对于孤立Mn2+发射发生蓝移和红移的原因,即534 nm和646 nm发光峰分别归属于AFM和FM耦合的Mn2+-Mn2+离子对。此外,Kamran等[48]在Mn2+掺杂CdS体系也建立了相应的掺杂模型,即用n=1,2,3,4,5个Mn2+替代超胞CdS中不同位点的Cd2+并赋予Mn2+不同的自旋磁矩,计算其d能级间的能量间隙。计算结果显示,当单个Mn2+离子掺入到CdS中时,ΔE(d-d)=2.176 6 eV,与低浓度Mn2+掺杂样品的发光能量相近。当相邻的Mn2+离子掺杂个数大于1并以FM耦合时,体系的ΔE(d-d)<2.176 6 eV;而当Mn2+离子间以AFM的方式发生耦合时,体系的ΔE(d-d)>2.176 6 eV。作者以此对发光光谱位置进行了指认。
Song等也发现在氟化物钙钛矿KMg1-xF3∶xMn2+(x=0.01~1)体系中[11](Mg2+只有一种格位,即Mn2+也只有一种格位),随着掺杂离子Mn2+浓度的增加,除了常见的红光发射峰(~600 nm)外还出现了新的近红外发光峰(~760 nm, 光谱形状及发光衰减如图4(a)~(d),也说明随着Mn2+浓度的增加,除了浓度猝灭效应外还可以形成新的发光中心。由于Mn2+最外层d电子与其他离子之间存在一定的离域相互作用,有可能形成一种磁极化子或自旋极化子,因此Mn2+离子掺杂浓度超过某个临界值时具有相互聚集和耦合的趋势。进一步地,通过对具有不同Mn2+-Mn2+距离的超胞模型进行第一性原理计算,结果表明具有反铁磁耦合的Mn2+-F--Mn2+距离最短的模型在结构优化后形成能最低(图4(e)),即最稳定(长程序的情况下)。对掺杂不同Mn2+浓度的样品进行Mn2+的扩展边X射线吸收精细结构(EXAFS)表征,也发现Mn2+-F--Mn2+(Mn2+-Mn2+离子对)的聚集现象,且出现聚集时Mn2+的浓度与出现近红外发光峰时的浓度相近,如图4(f);此外,从具有不同Mn2+-F--Mn2+连接构型(即键角)的变温光谱还可以进一步推断反铁磁耦合的Mn2+-Mn2+离子对是这个~760 nm近红外发光峰的发光中心,如图5[11]。
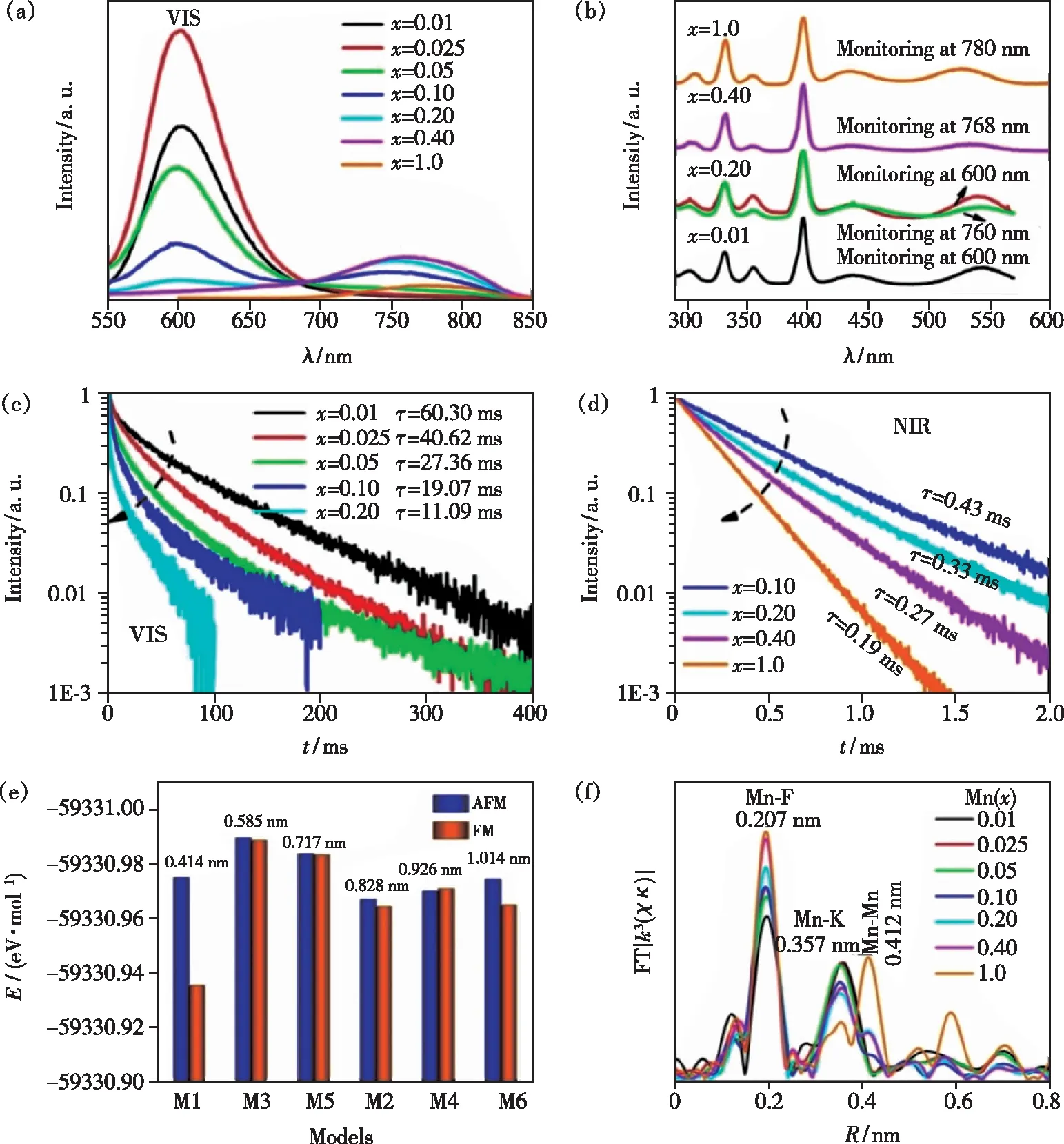
图4 (a)KMg1-xF3∶xMn2+(x=0.01~1)体系在396 nm激发光下的室温发射光谱;(b)KMg1-xF3∶xMn2+(x=0.01~1)体系的激发光谱;(c)VIS发射峰的荧光寿命;(d)NIR发射峰的荧光寿命;(e)两个AFM/FM耦合的Mn2+离子替代2×2×4 KMgF3超胞中Mg2+离子的六种可能模型的形成能(E);(f)KMg1-xF3∶xMn2+(x=0.01~1)体系的EXAFS谱[11]。
具体地,以具有完美钙钛矿结构的KMnF3(∠Mn2+-F--Mn2+为180°)、MnF6八面体间共顶点连接但有畸变的NaMnF3(∠Mn2+-F--Mn2+为141°~147°)和同时具有MnF6八面体共面连接和共顶点连接的CsMnF3(∠Mn2+-F--Mn2+分别为88°和177°)为对象,研究它们在10~300 K下的变温荧光光谱(如图5(a)~(c)所示)。发现KMnF3在10 K下具有656 nm和780 nm两个发射峰,其中前者归属于Mn2+的4T1到6A1跃迁发射,后者则归属于Mn2+-Mn2+离子对由∣6A14T1>到∣6A16A1>的发光。与KMnF3类似,NaMnF3在10 K下也同时具有600 nm和772 nm发射峰,可见发射峰强度随温度升高迅速衰减;近红外发射峰强度随温度升高而增强并在150 K达到最大,随后下降。CsMnF3在10 K下仅有一个600 nm发射峰,温度升高至50 K,另一个位于795 nm发射峰出现,可见发射峰随温度升高而红移。如前所述,Mn2+离子间的相互作用与Mn2+离子和配体的轨道重叠程度有关[49]。当Mn2+-F--Mn2+的键角越接近180°,Mn2+-Mn2+间轨道重叠程度最大,其耦合作用最强;当该键角发生较大畸变时,如在NaMnF3中Mn2+-Mn2+间的耦合作用减弱。上述三种材料的可见和近红外发光的变温行为是Mn2+-Mn2+间磁耦合作用、温度猝灭和d电子离域效应共同作用的结果。另外,在Mn2+掺杂的具有立方钙钛矿结构的KBF3(B=Mg,Zn,Cd)和ACdF3(A=K,Rb,Cs)体系中,Mn2+除了有可见(VIS)发射峰外,在700~900 nm范围还有一个近红外(NIR)发射峰(如图5(d)所示)。根据B位离子的大小,推测Mn2+-F-和Mn2+-Mn2+间距离在箭头方向的化合物中不断增加,VIS发射峰蓝移,这与单Mn2+离子的TS图相符,即晶体场强度减小,发射峰蓝移[28-29]。而NIR发射峰的红移则可能是因为距离增大而Mn2+-Mn2+间磁相互作用急剧减小导致的。
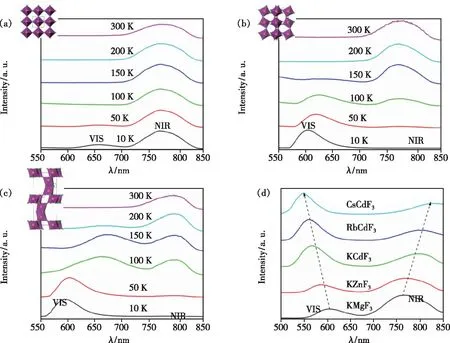
图5 KMnF3(a)、NaMnF3(b)和CsMnF3(c)的变温发射光谱;的室温上转换发光光谱[11]。
3.3 荧光寿命
研究者们早已注意到了Mn2+-Mn2+间磁相互作用可缩短Mn2+荧光寿命。如在Mn2+掺杂的MgS、SrS和CaS材料中[50-52],当Mn2+掺杂浓度大于某个值时其荧光寿命衰减曲线由微秒级快衰减和毫秒级慢衰减两部分组成,前者归因于Mn2+-Mn2+离子对的形成。1994年,Barthou等[53]发现在Mn2+掺杂的Zn2SiO4中,随着掺杂浓度的升高,室温寿命由15 ms衰减到1.75 ms,荧光寿命曲线由单指数衰减行为变为双指数衰减行为。作者也认为是Mn2+聚集形成Mn2+-Mn2+离子对导致的。但由于浓度猝灭的干扰,这一结论存疑。Vink等[22]利用海森堡-哈密顿量公式推导了AFM相互作用的Mn2+-Mn2+离子对最低激发态∣6A14T1>和基态∣6A16A1>的能级分布,提出当电子由∣6A14T1>跃迁到∣6A16A1>组态能级上时,某些裂分的能级跃迁ΔS=0,即自旋允许。孤立Mn2+的由4T1到6A1的电子能级跃迁是双重禁阻的,其荧光寿命长达毫秒级。当Mn2+与相邻Mn2+发生AFM相互作用时,部分自旋禁阻跃迁变为自旋允许跃迁,导致荧光寿命缩短。但由于多数研究对象为Mn2+掺杂的体系,随着掺杂浓度增加其存在浓度猝灭等因素的干扰,使得该理论缺少直接有效的实验证据。
为了排除浓度猝灭、声子等因素的干扰,Zhu等以纯锰基质材料CsMnCl3(CMC)和它的水合物CsMnCl3·2H2O(CMC·H2O)为研究对象,利用光磁测量技术来表征材料在有/无光照条件下自旋组态的变化,以期获得Mn2+-Mn2+磁耦合相互作用与其荧光寿命关系的更有效证据[14]。如图6(a)所示,CMC和CMC·H2O的发射峰分别位于646 nm和622 nm,两者在室温下的荧光衰减曲线均为单指数衰减(如图6(b))。具有较强声子能量的CMC·H2O的荧光寿命为275 μs,而具有较低声子能量的CMC荧光寿命明显比CMC·H2O短,约为159 μs。当温度为10 K时,CMC(τ=553 μs)的荧光寿命稍长于CMC·H2O(τ=424 μs),但也远小于孤立Mn2+的毫秒级荧光寿命。随着温度升高,CMC荧光寿命衰减速率比CMC·H2O快,且在250 K以后CMC的荧光寿命短于CMC·H2O[54]。通过与CMC·H2O对比,在排除了声子能量和浓度猝灭的因素后,可以肯定CMC荧光寿命的缩短与Mn2+-Mn2+磁相互作用有关。电子顺磁共振(EPR)、磁化曲线测试和DFT计算结果表明CMC具有强的AFM相互作用,其Weiss温度θ=-193.14 K,远强于CMC·H2O(θ=-41.63 K)。光磁测量结果显示CMC·H2O在光激发条件下的变温摩尔磁化率(χm)小于无光照条件下的变温χm(图6(c)),但相差不大;而Mn2+-Mn2+具有强反铁磁相互作用的CMC在光激发条件下的χm明显强于无光照的情况,特别是在TN温度以下(如图6(d)所示)。该现象可以通过图6(e)来解释,当光子将Mn2+电子由基态能级激发到激发态能级时,Mn2+的电子自旋总数发生变化,根据磁化率χ表达式[18]:
(3)
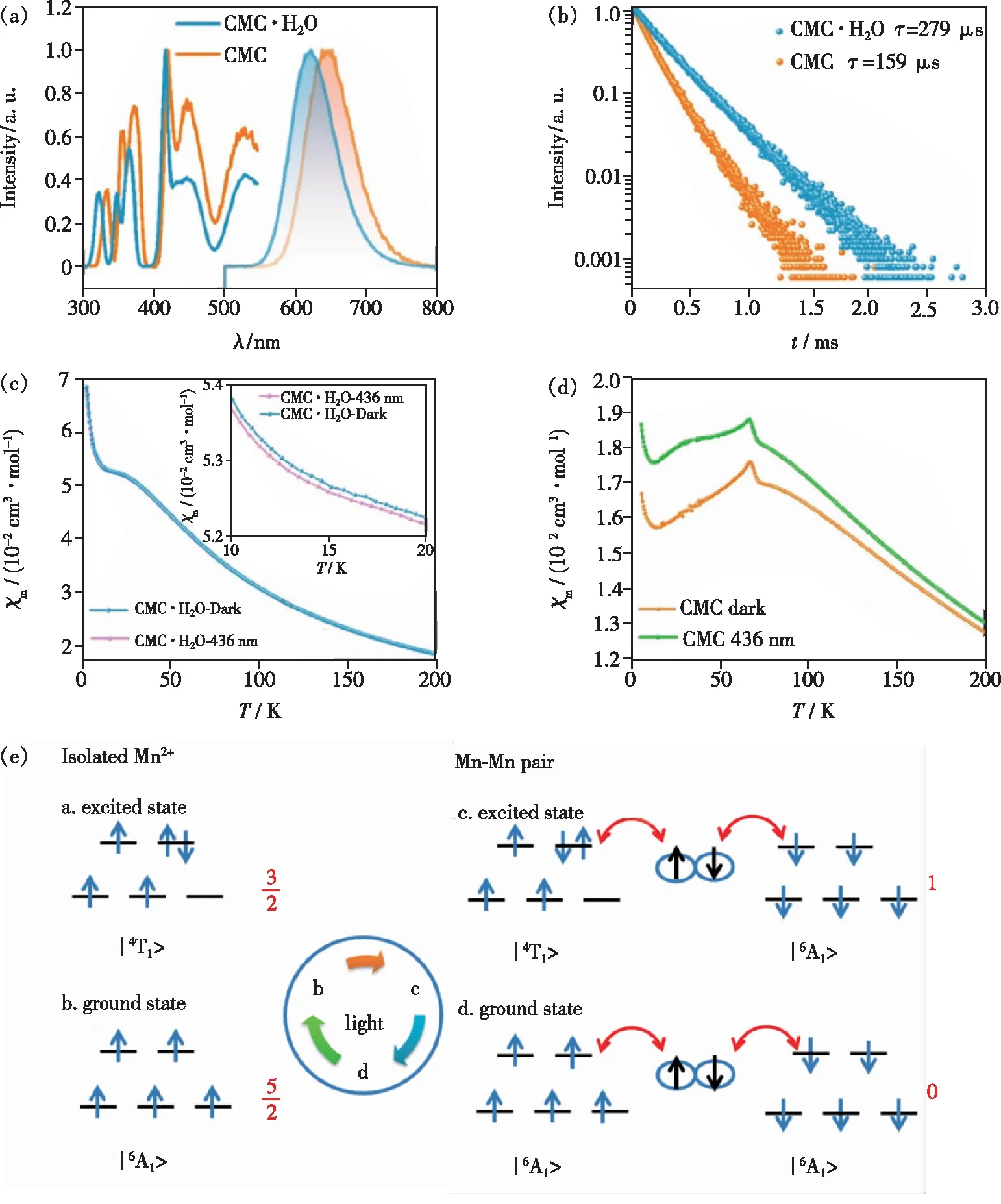
图6 CMC和CMC·H2O室温下的激发和发射光谱(a)以及荧光寿命(b);CMC·H2O(c)和CMC(d)在无光照(暗态)和436 nm光照射下的变温摩尔磁化率;(e)理想状态下孤立Mn2+和反铁磁相互作用的Mn2+-Mn2+处于基态和激发态的自旋状态[14]。
其中,N为阿伏伽德罗常数,μB为波尔磁子,k为玻尔兹曼常数,g为朗德因子,S为电子自旋总数。由公式(3)可知S与χ成正相关。对于孤立的Mn2+离子来说,电子处于基态能级时,S为5/2,电子跃迁到最低激发态能级时,S变为3/2;而对于具有理想的AFM相互作用的Mn2+-Mn2+体系来说,电子处于∣6A16A1>基态时,S为0;电子跃迁到∣4T16A1>激发态能级时,S变为1。据此可以推断,对于孤立的Mn2+离子,电子跃迁前后S变小,导致光激发下其χm变小;而对于具有AFM磁相互作用的Mn2+-Mn2+体系,电子跃迁前后S会变大。但实际情况会更复杂,因为在连续光照条件下处于光激发态(这里为了区别磁基态和磁激发态)的Mn2+相对于光基态的Mn2+少得多,且它们的浓度处于动态平衡中。此外,Mn2+处于光激发态的寿命也会影响光磁响应性质。对于CMC体系,在光照条件下部分Mn2+-Mn2+磁相互作用被破坏,此时存在b(孤立Mn2+光基态)、c(Mn2+-Mn2+光激发态)和d(Mn2+-Mn2+光基态)三种状态,整体的S仍然会大于无光照条件下的S,从而导致436 nm光照下CMC的χm大于无光条件下的χm。通过光磁测量技术可揭示Mn2+-Mn2+的AFM相互作用对其自旋组态的影响,进而影响其发光寿命。
此外,如果一个体系存在AFM和FM作用相互竞争的现象,会使Mn2+的发光衰减行为与前述不同。如在CsMnF3(CMF)体系中[55],室温下可以观测到两个明显分离的发光峰,一个位于600 nm(VIS),一个位于795 nm(NIR)(图7(a))。这两个发射峰都具有相似的激发光谱,但荧光衰减却截然不同。VIS荧光寿命仅47 μs,NIR荧光寿命长达1.45 ms(如图7(b)所示)。这与其他一些存在Mn2+-Mn2+磁相互作用诱导多峰发射的体系不同,通常在Mn2+掺杂的KZnF3和KMgF3中VIS和NIR发射峰室温荧光寿命均比较短,仅为几十微秒,在具有AFM相互作用的CMC中也仅159 μs[11,14,42]。低温下,CMC中具有AFM相互作用的Mn2+-Mn2+发光寿命约几百微秒,而CMF中VIS和NIR荧光寿命均比较长,分别为15.22 ms和9.80 ms。监测VIS和NIR两个发射峰在10~300 K温度范围内的变化趋势,发现前者的强度和荧光寿命随温度升高而急剧衰减,且峰位明显红移;而后者的强度和荧光寿命随温度变化的趋势则相对缓和,峰位几乎没有移动。结合材料晶体结构进行分析,CMF的MnF6八面体之间有两种不同的桥连方式,其中Mn1与Mn2八面体以共顶点线型连接(∠Mn2+-F--Mn2+为177.41°),Mn2与Mn2八面体以共面的形式连接(∠Mn2+-F--Mn2+为88.14°),不同的桥连方式可能导致复杂的磁相互作用,VIS和NIR发光的不同变温行为则可能是不同磁相互作用相互竞争的结果。利用磁性和光磁测量可揭示该相互竞争过程。磁性测量结果表明CMF的θ=-98.64 K,在53 K以下为AFM有序,场冷(FC)和零场冷(ZFC)曲线并不重合(如图7(c)所示),说明体系还存在铁磁或亚铁磁序;在53~100 K范围内,则表现出亚铁磁的行为。结合CMF的磁结构对此进行解释(如图7(d)所示),MnF6八面体共顶点连接的Mn1-Mn2具有强的AFM相互作用(J1<0);MnF6八面体共面连接的Mn2-Mn2间FM超交换相互作用(键角约90°,J2SE)和弱的AFM直接交换作用(J2DE),J2SE与J2DE共同决定Mn2-Mn2间磁相互作用(J2)。由于3d轨道半径较小导致其t2g轨道重叠程度小,使得J2DE通常都小于J1。由于轨道有效重叠程度的差异,在数值上J2也小于J1。在100~300 K温度区间内,热能大于|J1|,体系内Mn2+磁矩呈无序排列;当温度下降到100 K以下时,热能小于|J1|,三层共顶点的MnF6八面体形成呈亚铁磁有序排列;当温度下降到50 K以下时,热能小于|J2|,共面MnF6八面体间出现FM有序;但由于|J1|远强于|J2|,体系整体磁矩呈AFM排列。对材料进行光磁测量,结果显示在2~53 K温度范围内(图7(e)),436 nm光照条件下的χm大于暗态下的χm,体现AFM相互作用的特征,即Mn2+-Mn2+激发态自旋量子数大于其基态;在53~100 K范围内则相反,即436 nm光照条件下的χm小于暗态下的χm(图7(f)),即Mn2+-Mn2+激发态自旋量子数小于其基态。此外,通过对比具有AFM相互作用的CMC(图6(d)),可以发现CMF在TN以下光激发态与暗态的χm曲线差异小一些。这些都说明由于CMF中存在着复杂的磁相互作用的竞争,使得低温条件下VIS和NIR的荧光寿命显著大于具有相似结构的CMC。

图7 在395 nm激发下CMF的发射光谱(a)和荧光衰减曲线(b);(c)在1 000 Oe外场强度下CMF的变温摩尔磁化率曲线;(d)CMF中的磁相互作用:J1表示共顶点MnF6八面体间的(Mn1-Mn2) 180°超交换作用,J2DE表示共面MnF6八面体间的(Mn2-Mn2)直接交换作用,J2SE表示共面MnF6八面体间的(Mn2-Mn2)的90°超交换作用;CMF处于光照和无光照条件下的TN温度以下的变温摩尔磁化率曲线(ZFC表示零场冷)(e)及TN温度以上的变温摩尔磁化率曲线(f)[55]。
3.4 磁光现象
除了Mn2+-Mn2+离子间有磁相互作用以外,在半导体中掺杂Mn2+离子可以与半导体的激子发生sp-d磁交换作用,这种相互作用加剧Mn2+掺杂半导体能带结构的塞曼分裂,导致其分裂能比非掺杂半导体大两个数量级左右[56-58]。通常可用磁圆偏振发光光谱仪(MCPL)和磁圆偏振度(DCP(有时也用CP表示))对这种塞曼分裂进行表征。DCP可以通过公式(4)进行描述:
(4)
其中Iδ+和Iδ-分别为δ+和δ-偏振光的发光强度[59-61]。当掺入Mn2+离子时,材料的塞曼分裂从由半导体固有的本征性质主导转变为由Mn2+-激子的sp-d磁交换作用主导。Mn2+掺杂半导体的塞曼分裂随外磁场的增强逐渐饱和,相应的变磁场DCP曲线与用布里渊磁化曲线拟合的结果一致[56-57,62]。
由于Mn2+与激子存在sp-d磁交换作用,Mn2+-Mn2+磁相互作用对Mn2+掺杂半导体材料磁光现象的影响不易区分,鲜有文献报道相关的研究。尽管如此,在一些Mn2+掺杂体系中,当Mn2+浓度增加时其磁光行为出现一些异常,说明体系可能存在Mn2+-Mn2+磁相互作用。例如,2011年Viswanatha等[15]发现在Mn2+∶ZnSe/CdSe中将掺杂浓度从0.8 Mn/core提高到9.6 Mn/core,DCP值由40%下降至5%(如图8(a)所示),作者认为这可能是由于体系内Mn2+-Mn2+离子对的形成并增多导致的。2014年Bradshaw等[16]也探讨了Mn2+-Mn2+磁相互作用对Mn2+掺杂ZnSe半导体磁光现象的影响。作者依据Mn2+-Mn2+离子对的荧光寿命明显小于孤立Mn2+的特征,利用时间分辨的磁圆偏振发光光谱研究磁光现象并进一步探讨Mn2+-Mn2+离子对处于激发态的磁性质。在外磁场B=6 T、温度为1.7 K时,材料在590 nm处出现δ+和δ-的偏振发光(如图8(b)所示)。作者还测试了Mn2+掺杂浓度为0.52 %、1.5%和3.5% 的Zn1-xMnxSe样品的时间分辨磁圆偏振光谱。为分辨样品中Mn2+-Mn2+离子对的圆偏振信号,引入PTI和PTD:
(5)
(6)
其中PTI表示时间t趋向无穷时的DCP值,PTD表示从光发射第0秒与时间趋向无穷的DCP的差值。通常Mn2+-Mn2+离子对的发光衰减寿命比孤立Mn2+的荧光寿命小一个数量级以上[22,42,63],PTD可以表示Mn2+-Mn2+离子对的DCP值;而当时间t趋向于无穷时,Mn2+-Mn2+离子对的跃迁发射和激发能快速达到一个平衡状态,体系的偏振发光主要由具有长荧光寿命的孤立Mn2+的偏振发光贡献。测试表明不同掺杂浓度的样品在衰减时间分别为t= 0 ms和t>2.5 ms的变磁场强度下的圆偏振PTD(取t=0 ms,t>2.5 ms)和PTI(取t>2.5 ms)曲线与布里渊磁化曲线拟合的结果是不同的(如图8(c))。当t=0 ms时,无论高浓度还是低浓度掺杂体系,其变磁场PTD曲线与S=4的布里渊磁化曲线类似,特别是高浓度掺杂体系;而当t>2.5 ms时,低浓度掺杂体系的变磁场PTI曲线类似于S=3/2的布里渊磁化曲线,高浓度掺杂体系的变磁场PTI曲线与S=4的布里渊磁化曲线相似。这是由于t=0 ms时体系主要以Mn2+-Mn2+离子对的跃迁发射为主,所以无论高浓度还是低浓度掺杂体系其Mn2+-Mn2+离子对处于|6A14T1>激发态,其PTD曲线与S=4的布里渊磁化曲线相似。而PTI曲线包含了孤立Mn2+的发射和Mn2+-Mn2+离子对的发射和激发的快速动态平衡。当体系中Mn2+的掺杂浓度低,则PTI曲线以孤立Mn2+的跃迁发射为主;当体系中Mn2+的掺杂浓度升高,Mn2+-Mn2+离子对浓度增加,其磁相互作用增强并与孤立Mn2+的发光竞争,导致布里渊磁化曲线随掺杂浓度升高而逐渐由S=3/2的拟合趋向于S=4的拟合。通过DFT计算Mn2+-Mn2+离子对在|6A14T1>的交换耦合常数,Jdd=+1.36 meV>0,表明该能级以FM方式耦合。结合泡利不相容原理,由FM耦合的Mn2+-Mn2+电子能级分裂图(图8(d))可知当S=4时,其偏振发光在ms=4能级上跃迁只有δ+,这可以解释Zn1-xMnxSe体系在低温下随Mn2+浓度升高偏振发光减弱的磁光现象。
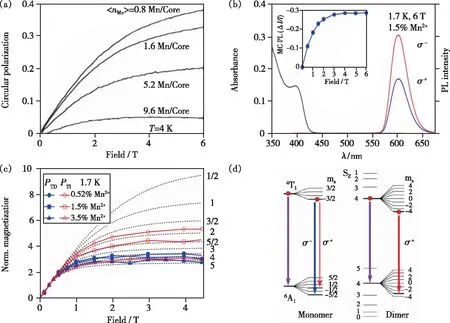
图8 (a)不同
目前,关于Mn2+-Mn2+磁相互作用对Mn2+掺杂半导体磁光现象影响的报道仍较少,主要是因为由于激子本征塞曼分裂、Mn2+与激子的sp-d磁交换作用、半导体的带隙宽度、激子与Mn2+间的能量传递、浓度猝灭以及量子限域效应等因素的影响使得相关研究变得复杂和困难。
4 关于Mn2+发光过程中磁相互作用存在与否的再探讨
要使Mn2+-Mn2+离子之间有磁相互作用,要求它们之间距离足够近,即在宏观上要求材料体系有一定量的Mn2+掺杂浓度(实验上可通过控制原料配比),在微观上两个Mn2+离子需尽可能接近(实验上可通过EXAFS等手段证明)。但距离只是空间上的必要条件,实验上仍然需要证明磁相互作用的存在。此外,要证明Mn2+-Mn2+离子对磁相互作用下的发光行为,除了要排除孤立的Mn2+在多格位的发光、发光浓度猝灭效应、声子等因素的干扰,最好还要把光与磁关联起来测试。下面简单地对比总结文献报道的一些方法,这些方法可提供或强或弱的证据。其中特别介绍光磁测量技术在该类研究中的应用。
4.1 磁化强度
测量磁化强度以获得变温磁化率,然后根据Curie-Weiss定律求得Weiss温度θ,根据其数值的正负号来判断铁磁/反铁磁耦合作用是最常用的手段,如图1。还可以通过磁滞回线数据来判断有无铁磁性。但对于Mn2+掺杂的材料体系特别是掺杂浓度较小时,该方法的灵敏度较低。而且由于存在浓度猝灭、多格位占据等干扰因素,该方法不能有效地确定磁相互作用与发光的关系。
4.2 DFT计算
DFT计算可以从理论上计算掺Mn2+的材料不同磁结构的相对稳定性(能量高低)和其d能带带隙[11,14,16,47-48,64-66]。例如Kamran等[48]通过构建1~5个Cd2+被具有不同自旋磁矩的Mn2+取代的CdS超胞结构模型,计算这些具有不同Mn2+-Mn2+距离的模型的能量和它们的d能带带隙(Ed-d)。计算结果如前所述,当Mn2+离子以FM方式耦合时,Ed-d<2.176 6 eV,其发射峰相对于孤立Mn2+发生了红移,且其Ed-d随着Mn2+离子对浓度的增加而减小。这与实验结果符合较好。DFT还可以计算缺陷对Mn2+-Mn2+磁耦合作用的影响。Khan等[67-68]通过构建具有Zn/S/Se空位缺陷和Mn2+聚集的ZnS、ZnSe结构模型,利用DFT计算这些模型中Mn2+-Mn2+以AFM和FM耦合时的总能量和光吸收系数并与无缺陷模型进行比较。计算结果表明,当存在Zn空位缺陷时,体系基态的磁耦合方式由AFM转变为FM,同时费米能级附近出现缺陷态使得带隙变窄,d-d跃迁能量减小。虽然上述结果并没有直接计算d电子的激发态,它仍然可为研究Mn2+-Mn2+磁相互作用的类型及其对发光的影响提供重要参考。
4.3 EPR
EPR可以给出材料中未成对电子的状态信息。当未成对电子的晶格环境发生变化或受到相邻原子未成对电子相互作用的影响时,其在外磁场下自旋能级的分裂能会发生改变,导致其EPR吸收峰展宽或者位移[19,69]。55Mn具有I=5/2的核自旋磁矩,在外磁场作用下核自旋磁矩与未成对电子磁矩相互作用使能级发生分裂,在EPR谱上显示为6个精细谱线,分别与核磁矩mI=-5/2,-3/2,-1/2,1/2,3/2,5/2相对应。当Mn2+离子与相邻Mn2+发生偶极-偶极相互作用和磁(自旋交换)相互作用时,其EPR谱线的精细结构消失[70-73]。由于Mn2+-Mn2+离子间的偶极-偶极相互作用和磁相互作用对其EPR峰宽的贡献不同(前者使EPR峰展宽,后者使EPR峰变窄),因此可以通过对比EPR峰宽(ΔH)的大小来判断Mn2+-Mn2+离子间的偶极-偶极相互作用或磁相互作用的相对强弱[74-75]。有研究者还用EPR谱线的峰强和峰宽来推断材料中Mn2+-Mn2+磁相互作用类型和强度[73]。因EPR峰强与材料的磁化率χ成正比,对EPR谱线进行二重积分可得到峰强。记录变温条件下的EPR谱线并利用Curie-Weiss公式对其积分曲线进行拟合,可以得到材料的居里常数(C)和Weiss温度θ,进而可推导出材料中Mn2+-Mn2+磁相互作用的类型与强度。虽然用该方法得到的C/θ不够精确,但也可以粗略判断材料中有无磁相互作用。
4.4 光磁测量
光磁测量技术常用于研究光敏材料中光诱导的电荷转移过程[76-81]。如在CoFe普鲁士蓝中,无光照条件下Co3+LS-Fe2+离子对(LS为低自旋态,总S=0)具有AFM相互作用。在光照条件下,一个电子从Fe2+转移到Co3+上,形成亚铁磁耦合的Co2+LS-Fe3+离子对,然后它通过自旋翻转变为Co2+HS-Fe3+(HS为高自旋态,总S=1)。根据S与χ的关系(公式(3)),材料χ大小与S成正相关,利用光磁测量技术可以有效测得材料在光照前后磁化率χ变化,从而判断是否发生光诱导的电荷转移过程[82]。
Mn2+掺杂的发光材料在光激励过程中虽然不会发生电荷转移,但Mn2+-Mn2+离子对的自旋组态会明显区别于孤立的Mn2+,它们在有/无光照的条件下自旋总量子数S会有差异,用光磁测量技术可能区分出来。例如在前面提到的CMC及其水合物中,具有AFM相互作用的Mn2+-Mn2+离子对在光照条件下的磁化率大于无光条件下的磁化率,这与孤立的Mn2+或FM耦合的Mn2+-Mn2+离子对的情况相反;利用光磁测量技术可证明Mn2+-Mn2+自旋量子数的变化,推断其可以部分打破Mn2+自旋禁阻跃迁旋律进而缩短荧光寿命[14]。
4.5 磁光效应
对于Mn2+掺杂的半导体,Mn2+-Mn2+离子对在外磁场下的能级分裂不同于孤立的Mn2+。如图8(d)所示,对于孤立的Mn2+,其最低激发态4T1分裂为4个ms项,分别为ms=3/2,1/2,-1/2,-3/2;基态能级6A1分裂为6个ms项,分别为:ms=5/2,3/2,1/2,-1/2,-3/2,-5/2。根据选择定则,Δms=±1的跃迁是允许的,因此孤立Mn2+在ms=3/2,1/2,-1/2,-3/2均可以发生δ+和δ-的偏振发光。对于Mn2+-Mn2+离子对,其基态能级为|6A16A1>,最低激发态能级为|6A14T1>,能级在磁场作用下可发生劈裂,如图8(d)所示。根据选择定则Δms=±1,电子在一些激发态能级跃迁缺少δ+项,而另一些激发态能级跃迁缺少δ-项,当电子在Mn2+-Mn2+离子对的各个激发态能级布居不均时将会导致δ-和δ+偏振发光强度不同。例如在Zn1-xMnxSe中[16],假设电子主要由S=4激发态能级跃迁到S=4基态能级(如图8(d)所示);在磁场作用下,S=4激发态能级分裂为9个ms项,分别为ms=4,3,2,1,0,-1,-2,-3,-4;S=4基态能级具有9个ms项,分别为ms=4,3,2,1,0,-1,-2,-3,-4。由于不存在ms=5和ms=-5项,电子在ms=4激发态能级跃迁缺少δ+项,在ms=-4激发态能级跃迁缺少δ-项[16]。此外,由于Mn2+-Mn2+磁相互作用导致材料内部存在分子场,其磁场强度通常远大于外加磁场,使得作用在Mn2+-Mn2+离子对与孤立Mn2+的有效磁场强度不同[83]。因此,它们的磁光现象会有所差别,实验中可以观察到磁耦合的Mn2+-Mn2+的异常磁光行为。例如,在一些体系中(如Mn∶ZnSe/CdSe纳米晶[15]和Zn1-xMnxSe[16])可以观测到随Mn2+掺杂浓度升高Mn2+的圆偏振发光减弱,其变磁场的DCP饱和值下降。2014年,Bradshaw等通过时间分辨磁圆偏振发光光谱给出了部分强有力的实验证据[16]。虽然目前不能很清晰确切地解释Mn2+-Mn2+磁相互作用对磁光效应的影响,但用MCD、MCPL这些数据结果仍然能说明磁耦合Mn2+-Mn2+离子对的存在。
5 潜在应用
Mn2+掺杂荧光材料可应用于照明显示等领域。由于孤立的Mn2+荧光寿命长,用Mn2+掺杂的荧光材料制作的显示屏容易出现人眼可察觉的画面拖尾现象[23,53,84]。此外,在荧光粉+近紫外LED芯片的照明器件中,Eu2+/Mn2+共掺的荧光粉是最具潜力的备选红色荧光粉材料[6,85-88],但大功率辐照(>10 W/cm2)容易引起具有长荧光寿命的Mn2+掺杂荧光粉材料发光饱和从而抑制器件光电效率的提升[8]。Mn2+-Mn2+离子对的从|6A14T1>到|6A16A1>的跃迁可以部分打破Mn2+自旋禁阻选律,使其荧光寿命由毫秒级缩减至微秒级,实验证明相应的荧光材料可抑制Mn2+的发光饱和[14]。
此外,磁耦合的Mn2+-Mn2+除了能发射可见光外还可能发射长于700 nm波长的近红外光,使得相应的材料在夜视等领域具有潜在应用。例如,Song等[13]发现,在Mn2+掺杂的MgAl2O4中,当掺杂浓度达到0.1时,其在450 nm光源激发下可发射~825 nm的近红外光;当掺杂浓度升高至0.5时,其发光强度达到最强。作者把该近红外光归属于磁耦合的Mn2+-Mn2+;用环氧树脂将MgAl2O4∶0.5Mn2+封装在蓝光InGaN LED芯片上,在120 mA、27 V驱动下器件的输出功率为78.41 mW。用该器件作为近红外光源时,在黑暗处也可以清晰地看到物品的形状。掺Mn2+近红外发光材料在高分辨与高透射深度的生物成像领域也具有潜在应用前景。
6 结论与展望
本文综述了Mn2+-Mn2+离子间磁相互作用的原理、类型及其发光特性和研究进展。大量实验表明,磁耦合的Mn2+-Mn2+在Mn2+掺杂发光材料中比较常见,Mn2+-Mn2+离子对的形成在光激励的过程中可以部分打破Mn2+电子自旋禁阻跃迁选律从而缩短其荧光寿命、影响Mn2+掺杂半导体材料相关能级的塞曼分裂导致磁圆偏振效应减弱。除此之外,Mn2+-Mn2+离子对还可以作为新的发光中心,带来更丰富的发光颜色。根据耦合方式的不同,Mn2+-Mn2+磁相互作用主要分为FM和AFM,但在Mn2+掺杂体系中难以辨认它们,导致该类研究经常存在争议,需要深入探索其微观本质。在掺杂体系特别是半导体中,根据掺杂浓度和离子占据格位情况,Mn2+有可能以孤立、二聚或多聚的形式存在。但在实验上证明和确认这些聚集体依然很困难,而且通常很可能是多种聚集体共存的情况。在有机-无机杂化材料或半导体簇合物中,可通过分子设计构建Mn2+孤立、二聚或多聚的模型化合物。目前只有少量文献讨论这些模型结构的发光性质[38,75,89-91],但仍缺乏磁相互作用与发光之间的系统研究。此外,在Mn2+多聚体中还可能存在相互竞争的磁作用,使得磁结构相当复杂甚至出现磁阻挫行为,研究其与发光性质之间的关系虽面临巨大挑战但却是非常有意义的工作。值得注意的是,带电荷的具有顺磁性的缺陷也会与Mn2+发生磁相互作用,导致体系出现更复杂的磁、光性质。总之,Mn2+-Mn2+磁相互作用是一种典型的微观自旋-自旋相互作用,其对发光性质的影响或者调控是一项充满挑战的研究。该类研究在量子操控领域可能具有重要的理论指导意义。目前,通过光磁测量技术、磁光测量、EPR测试以及DFT计算可以判断是否存在磁耦合Mn2+-Mn2+离子对。含有磁耦合Mn2+-Mn2+离子对的发光材料除了在照明显示领域有重要应用外,在一些自旋光电子器件和响应磁场的光器件中也有潜在应用。随着科技的进步,研究人员在该交叉领域还可能挖掘出一些新概念和新器件原型。
本文专家审稿意见及作者回复内容的下载地址:http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20220006.
