河道堤防软土层抗拔受力计算方法改进及工程应用

2022-05-05曹婷婷

水利技术监督 2022年5期

曹婷婷

(桓仁满族自治县水务局，辽宁本溪 117200)

在河道整治工程中，对于具有软土地基的河道堤防首先需要对地基抗拔受力进行计算，从而分析河道堤防的稳定性[1]。在国内许多河道堤防工程设计中，软土地基抗拔受力主要采用荷载传递方法进行计算[2-7]，但该方法由于未能考虑河道堤防软土地基的自重，土体抗拔受力计算精度不高，而土地抗拔受力计算精度高低将直接影响河道堤防的稳定设计，为提高河道堤防稳定设计，保障汛期河道堤防的安全运行，亟需对河道堤防软土地基抗拔受力计算精度提高进行研究[8]。近些年来，有研究学者在软土地基土力学计算中，通过引入土体自重因子，对抗拔受力计算方法进行改进，并在一些水库、水闸工程建设项目中得到具体应用[9-15]，应用效果均表明相比于传统方法计算精度有所改进，但在河道堤防工程设计中还未得到具体应用，本溪地区中小河流堤防大都为软土地基，为提高其河道堤防稳定性，本文引入土体自重因子，对抗拔受力传统荷载传递方法进行改进，并结合工程实际现场测定数据，对改进前后计算方法的精度进行对比，研究成果对于于河道堤防稳定性计算具有重要的参考价值。

1 改进方法原理

传统软土地基抗拔受力主要是对不同单元的荷载进行承载力的计算，计算方程为：

ΔT=ΔRtanφ+cΔL

(1)

式中，ΔT—垂向承载力，kPa；φ—土层之间的摩擦力，kPa；c—土层之间垂向的切应力，kPa；ΔL—土层受力面之间的宽度，mm；ΔR—垂向切应力的变化量，kPa。

ΔR的计算方程为：

ΔR=ΔQcosθ+KpΔQsinθ

(2)

式中，Kp—垂向压力荷载传递系数；θ—软土地基水平方向夹角(°)；ΔQ—软土地基土层抗拔方向夹角(°)；其余变量含义同前所述。

ΔQ的计算方程为：

ΔQ=γ(H-Z-ΔZ/2)ΔL

(3)

式中，γ—土体自重因子，kg；Z—土体垂向距离，mm；H—土体水平距离，mm；其余变量含义同前所述。

采用静力学方程对土体单元抗拔受力进行计算：

PV+μqπx2-μπ(q+Δq)(x+Δx)2-

ΔW-2μπ(x+Δx/2)ΔTsinθ=0

(4)

式中，x—土体重心到受力点之间的距离，mm；Δx—变动长度，mm；u—圆周比；Pv—抗拔受力计算的静止荷载，kPa；q—单位土体抗拔承载力，kPa。

采用微分方程求解原理对静力学方程进行计算：

(5)

其中河道堤防软土地基不同方向荷载计算方程为：

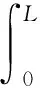
(6)

式中，WP—软土地基的自重，kg；L—河道堤防软土地基的总长度，m；τmax—剪切应力的最大计算值，kPa。

τmax的计算方程为：

τmax=Kσvtanφ′+c′=kγztanφ′+c′

(7)

式中，φ′—土层内摩擦力计算值，kPa；K—垂向应力比。

2 工程实例应用

2.1 河道堤防软土地基特征参数

以本溪地区某中小河流治理工程为典型实例进行软土地基抗拔受力计算。主要采用桩固结构进行软土地基的稳定加固。软土地基加固长度为1.5km，工程主要软土地基土地以及桩固测定的主要特征参数见表1。

表1 河道堤防软土地基土及桩固特征参数

2.2 软土地基变形位移计算对比

分别采用改进前后的河道堤防软土地基抗拔受力计算方法计算滑块变形位移，对比结果见表2。

对不同土体纵向深度的位移变化进行沿程分析，如图1所示。

由改进前后软土地基抗拔受力分析计算结果可看出，改进方法的变形位移量相比于改进前有所减小，改进后的抗拔受力分析方法由于综合考虑软土地基土体自重因子的影响，使得其纵向深度西的切向应力有所减小，从而相对减少不同纵向深度的土层变形位移量。由表2还可看出随着纵向深度的不断增加其土层变形位移量逐步较大，随着纵向深度递增土层均值变化有所减小从而加大了变形位移量。由图1可看出，改进前后纵向深度的变形位移总体呈现非线性变化，改进方法的纵向变形位移总体偏右，在相同纵向深度改进方法的土层变形位移均小于改进前，河道堤防软土地基土体和桩体在纵向深度的变形位移具有一定的相似性，这主要是因为土体和桩体均受土层荷载力影响，当纵向深度增加后其外扩变形位移有所增加。

表2 土体及桩体变形位移计算对比结果

图1 软土地基桩体和土体纵向深度的位移变化

2.3 改进前后土体变形量计算对比

分别采用改进前后的抗拔受力计算方法对研究河段堤防软土层的变形量进行计算，并根据现场测定值对计算结果进行对比分析，结果见表3。

表3 改进前后河道堤防软土层变形量计算结果对比单位：mm

由改进前后研究河段堤防软土土层变形量计算对比结果可看出，改进后的方法相比于改进前土层变形量计算误差可减小约15%。通过增加土层自重因子，一定程度提高了纵向深度土层之间的静力荷载，使土层之间的变形量计算精度得到不同程度的提高。由不同静力荷载作用的变形量可看出，随着荷载力的增加变形量呈现先微弱递增后明显递增的变化，这主要是因为随着静力荷载的增加，土层变形位移加大，使得河道堤防软土层的变形量加大。

2.4 静力荷载作用的抗拔受力

采用改进的荷载计算方法对不同静力荷载作用的抗拔受力进行计算，并分析其静力荷载作用的河道堤防软土地基土体和桩体的变形量，计算结果见表4—5。

表4 不同静力荷载作用的河道堤防软土地基土体变形量计算值

对不同静力荷载作用的变形量分布进行统计，如图2所示。

图2 不同静力荷载作用的软土地基的土体和桩体变形分布曲线

从不同静力荷载作用的河道堤防软土层变形分布可看出，当静力载荷从300kN递增到900kN后，随着静力荷载的增加其河道堤防软土层逐步被压实，降低了土层之间的内摩擦力，增加了其软土层之间的黏聚力。此外随着纵向轴力的增加，同一个静力荷载作用的抗拔受力逐步增加，纵向深度下的变形量也将有所增加。从不同静力荷载作用的软土地基的变形分布曲线可看出，随着静力荷载的增加，其土体和桩体变形量总体呈现二次曲线变化，随着横向应力的增加，其土层滑块变形量逐步加大，当横向应力最大时，其变形量达到最大，后逐步趋于稳定，当达到土层极限荷载后抗拔强度达到最高值，随着抗拔强度不再发生变化，其变形量也将趋于稳定。从软土土层的桩体变形分布曲线可看出，相比于土体，其桩体不同横向应力的变形位移变化幅度更大，这主要是因为桩体的侧压力系数要高于土体，使得其横向应力的变形位移量要高于土体。从土体和桩体不同静力荷载的变形分布曲线可看出，当静力荷载取值为900kN时可作为其外包线进行抗拔强度的计算。