Logistic-Sine映射与比特重组的图像加密算法

唐传华，巫朝霞

（新疆财经大学 统计与数据科学学院，乌鲁木齐 830011）

0 引 言

数字图像是生物统计学、医学、军事、在线个人相册等领域最重要的信息载体之一。如一张自拍，可以描述人们的外貌，也可以反映其大致的年龄和健康状况。因此，如何保证图像信息具有安全的输入输出环境是一个很大的挑战。在各种图像安全技术中，最常用且有效的措施是图像加密技术。

混沌系统用于密码学是非常合理的，并且广泛应用在图像加密领域。庹朝永等提出一种新的彩色图像加密算法，该算法首先通过二维Logistic混沌映射产生伪随机序列进行像素置乱，然后联合比特异或与随机重组将各像素值转换为相应的二进制，最后对每个24位像素值进行RGB 3种颜色重新组合得到新的加密图像，然而该算法计算强度与空间需求偏高；廖春成等利用明文像素值来计算混沌系统的参数和预迭代次数，有效提高了明文敏感性。该算法通过Kent混沌系统迭代产生混沌序列实现全局置乱，然后进行比特级置乱得到加密图像。Yueping Li等提出了一种基于高维混沌的图像加密算法，该算法通过5维多翼超混沌系统产生的密钥流与原始图像有关，然后分别运用像素级置乱和比特级置乱来混淆图像像素位置，最后使用扩散操作来改变像素值；伍朝阳等提出一种结合像素置乱与比特置乱的超混沌Chen系统，对图像进行加密的算法；胡春杰等提出了一种新的二维离散型混沌映射，并利用改进的Logistic映射，对图像进行置乱操作，然后进行异或运算和比特位的交叉换位得到最终密文图像。

本文设计了一种基于Logistic-Sine混沌映射与比特重组的图像加密方法，首先利用Logistic-Sine混沌映射对明文图像进行全局置乱，然后通过比特重组操作将经过全局置乱的图像转化为中间密文图像，最后经过水平方向扩散的比特异或得到最终的加密图像。最后的仿真实验分析说明：该算法可以抵御各种类型的攻击，有较高的安全性和稳定性来保护图像。

1 Logistic-Sine映射与比特重组

1.1 Logistic-Sine映射

传统的一维Logistic和Sine映射虽然被广泛应用在图像加密中，但依然存在很大的局限性。如：其仅在相应的参数范围内处于混沌状态，但依然存在一些参数并不处于混沌状态。因此，本文设计了一种由Logistic和Sine映射延伸推导得出的Logistic-Sine混沌映射，其表达式如式（1）：

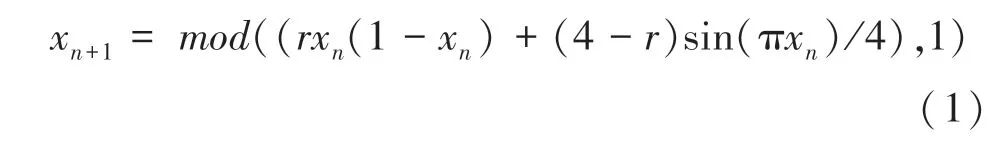
其中，模函数（）表示取模，返回余数。

经过模运算后，循环迭代可以得到一个取值在0～1之间的混沌序列。虽然，模运算会加大运算量和加密时间，但是通过增加模运算，使得Logistic-Sine映射的参数的范围不仅仅局限于（0，4］之间，并且扩大了系统的混沌区域，同时加密系统的密钥空间也会相应扩大，可以更好的抵抗穷举攻击。

图1（a）～1（b）分别是Logistic-Sine映射的分岔图和Lyapunov指数变化图。从图中可以看出，Logistic-Sine映射在整个参数范围内都处于混沌状态，且分布均匀。由此说明本文设计的Logistic-Sine映射，混沌性能比较优越，用于图像加密过程是可行的。

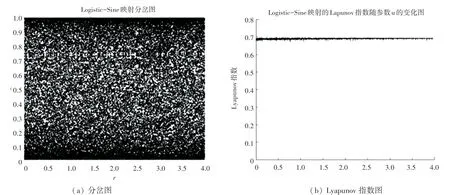
图1 Logistic-Sine相关图Fig.1 Logistic-Sine correlation diagram

1.2 比特重组

现有的混沌系统图像加密思路可以从两方向入手：一是在像素的基础上对图像进行加密，将像素作为最小的元素加以研究，而数字图像就是所有像素的集合；二是在比特级的层次上对图像进行加密，将每个十进制像素值转换为二进制值，同时划分为若干个比特平面，并继续在这些比特平面上进行比特级操作。例如，256级灰度图像中的每个像素值可以转化为对应的8位二进制数来表示，这时可以将一幅256级的灰度图像划分为8个比特平面，第（1，2，…，8）个比特平面就是所有像素的第个比特值的集合，而且比特平面位级越高，其中包含的原始图像的有用信息就会越多。

基于比特的图像加密算法是近些年才被提出来的，其可以在比特级层次上同时改变像素位置及其像素值。本文就是在比特级的层次上对图像进行加密，将Logistic-Sine混沌映射和比特重组相结合，该算法在安全性、稳定性等方面表现出了优越的特性。

2 加密算法过程

图像加密算法分为置乱、比特重组和扩散3个阶段。第一阶段的置乱过程是利用Logistic-Sine映射迭代，产生混沌伪随机序列，进行全局置乱。第二阶段的比特重组过程，是将全局置乱后的十进制矩阵经过比特重组操作，得到中间密文图像。第三阶段的扩散过程是将中间密文图像经过水平方向扩散的比特异或操作，得到最终的密文图像。 本文加密算法流程如图2所示。

图2 图像加密算法流程图Fig.2 Flowchart of image encryption algorithm

2.1 置乱

置乱过程的具体实现步骤如下：

（1）选取一幅大小为的明文图像，利用式（2）和式（3）计算像素矩阵中所有像素值的总和sum和平均像素值，然后利用式（4）、（5）分别计算出Logistic-Sine混沌系统的控制参数和初始迭代的次数。

其中，是与明文密切相关的量，可以有效抵抗选择对明文的攻击。

（2）将输入的初始密钥（，）带入到式（1）。

其中，是随机输入的控制参数。预迭代次后去掉前个迭代值，可以消除暂态效应的影响。

（3）全局置乱将分别进行行置乱和列置乱。

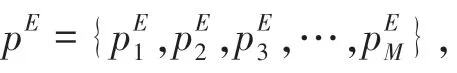
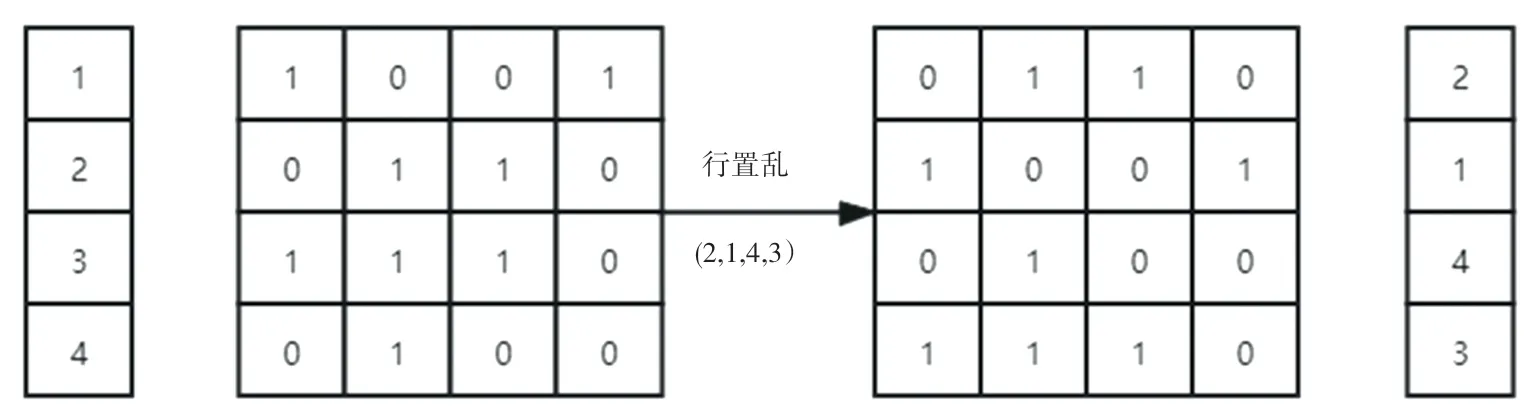
图3 行置乱示意图Fig.3 Schematic diagram of row scrambling

2.2 比特重组

将经过置乱阶段得到的十进制矩阵进行比特重组操作，得到中间密文图像矩阵。具体步骤如下：

（1）利用Logistic-Sine混沌系统继续迭代次，生成一个长度的混沌序列｛，，，…，q｝。

（2）将十进制矩阵依据行优先原则转化为一维混沌序列｛，，，…，r｝，同时将其像素值r转化为对应的二进制数。如，取出的像素值r＝145，则对应的二进制数为10010 001。

（3）通过比较序列中相邻像素的大小，对序列的像素值r进行比特重组。操作过程如下：

图4 比特重组示意图Fig.4 Schematic diagram of bit reassembly

2.3 扩散

在本文的图像加密算法中，使用水平方向的扩散。将中间密文图像作为输入端，从图像的第一个像素开始，依次逐行向前移动。在此过程中，依据行优先的原则，保留第一行第一个像素不变，对第一、二个像素进行比特异或得到新的第二个像素，将其与第三个像素进行比特异或得到新的第三个像素，以此类推，直到最后一行的倒数第二个像素与最后一个像素进行比特异或结束。经过水平方向的扩散操作，可以得到最终的密文图像。 具体算法如下：

以上是图像加密的算法过程。而解密算法其实就是加密算法的逆过程，在此不再赘述。

3 实验结果与分析

在本文的实验过程中，选取256×256的Lena灰度图，在Win10操作系统下，以MATLAB R2017a为软件工具模拟仿真实验过程。设定Logistic-Sine混沌系统的初始密钥（，）（0.234，0.128）。对Lena图进行加密和解密后的图像如图5所示。

图5 加解密效果Fig.5 Encryption and decryption effect

由图中可见，该算法加密效果较好，既可以很好的隐藏原文信息，又可以很好地恢复原文图像。一个好的加密算法应该能够抵抗各种攻击，因此对该算法进行了密钥空间分析、统计分析和密钥敏感性分析等，验证了该算法的安全性和稳定性。

3.1 密钥空间分析

密钥空间是指在加解密过程中需要用到的密钥总数，密钥空间的大小影响着加密算法能否有效抵抗穷举攻击。本文算法采用Logistic-Sine混沌系统的2个参数（，）作为初始密钥，计算机系统可以处理64位数据，且数据设为双精度浮点类型，则密钥空间为2。一个理想的加密算法需要有足够大的密钥空间来抵御穷举攻击，其值不应该小于2。显然，本文加密算法具有足够大的密钥空间。

3.2 统计分析

良好的图像加密算法应该对任何形式的统计攻击都具有稳定性，因此可通过直方图、相邻像素间相关性和信息熵来分析加密算法的抗统计攻击能力。

3.2.1 直方图

图像直方图通过绘制图像的像素值来说明图像中的像素分布。理想的加密算法应该拥有均匀分布的密文直方图，因为其需要隐藏明文的有用信息。本文加密算法生成的明文图像及密文图像的直方图分布如图6所示。密文图像的每个像素值近乎相等，呈现均匀分布，因此没有给攻击者提供任何使用统计攻击的有用信息，使其很难通过统计分析的方法来破解原始明文图像。

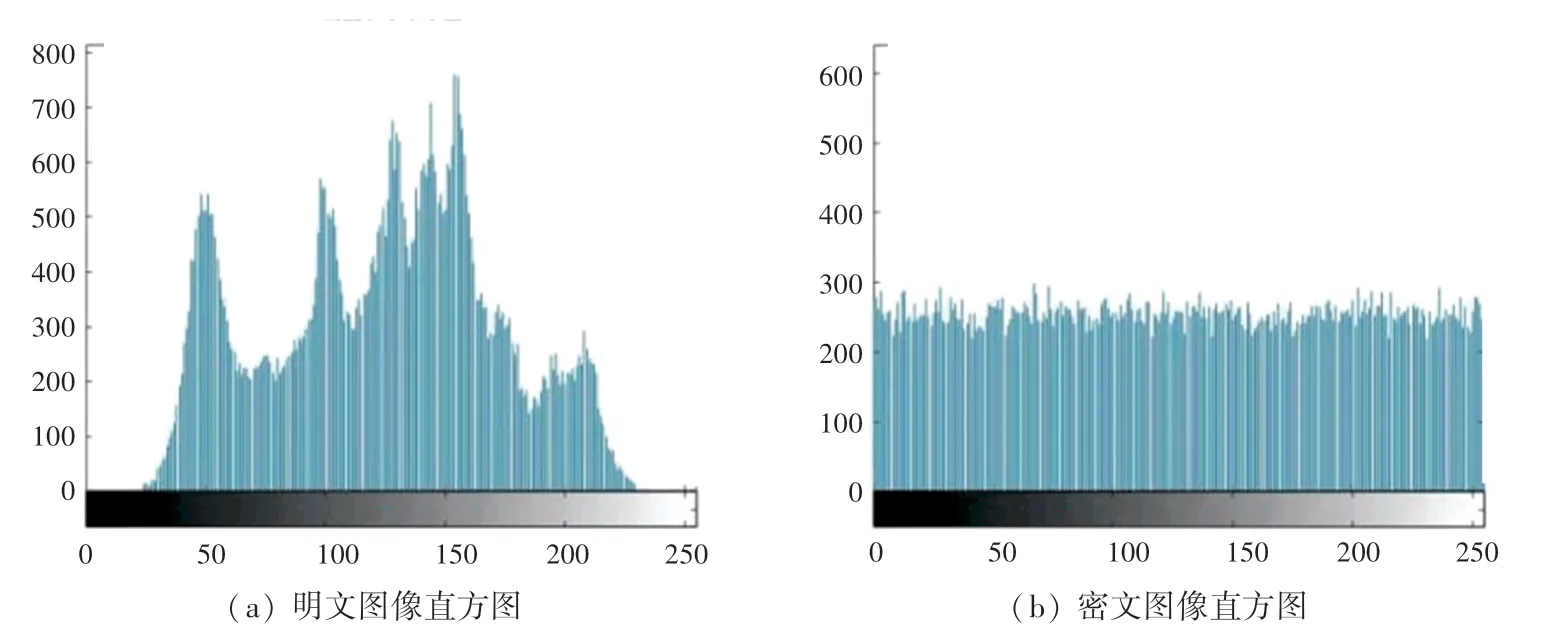
图6 明文与密文图像直方图Fig.6 Histogram of plaintext and ciphertext images

3.2.2 相邻像素间相关性

良好的加密算法应使密文图像相邻像素的相关系数足够低，用来抵御统计攻击。为了分析明文图像和密文图像中相邻像素的相关性，分别选取水平、垂直和对角方向上的相邻像素加以分析，相关性分布如图7所示。明文图像中相邻像素的分布比较集中，说明明文图像相邻像素相关性较高；密文图像中相邻像素比较离散，说明密文图像相邻像素相关性较低。相邻像素相关性计算公式如下：

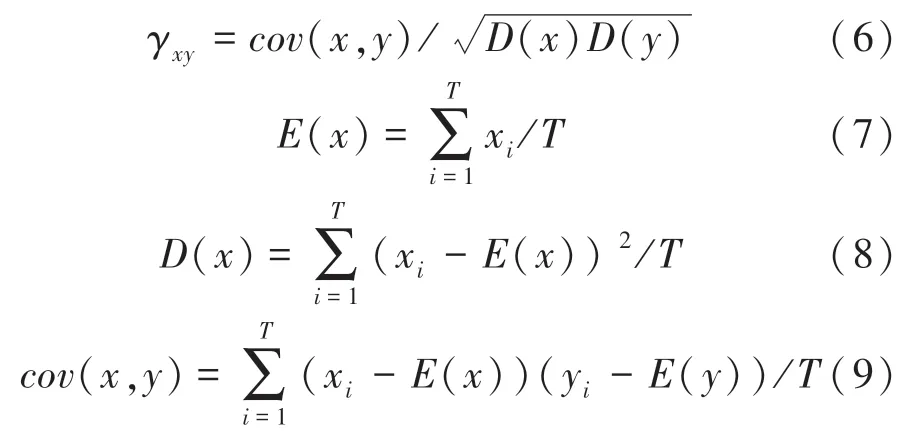
其中，、是图像中两个相邻像素的灰度值，为图像中选择的像素总数。

通过选取加密算法较好的3种算法与本文算法进行对比（对比结果见表1）发现：本文提出的算法在水平、垂直、对角3个方向的相关系数都接近于0，可以很好的消除相邻像素相关性；信息熵值更接近理想值8；值均超过0996、值均超过0334，能够有效抵抗差分攻击等攻击手段。因此，该加密算法可以很好的应用到图像加密过程中。

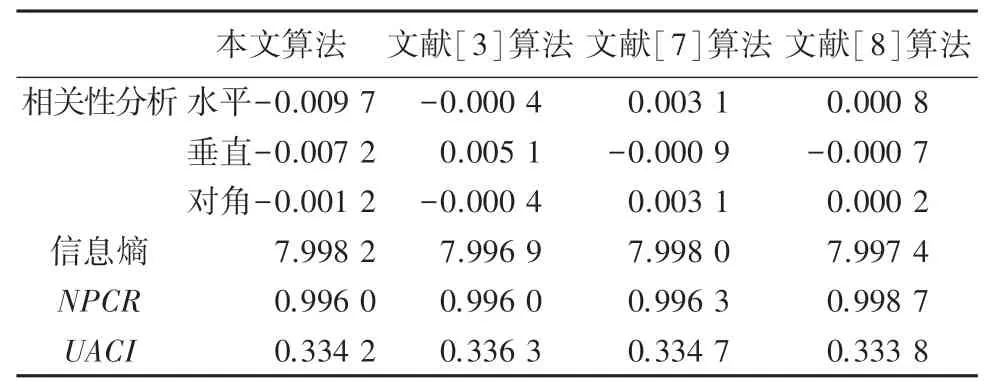
表1 本文算法与文献［3，7，8］结果对比Tab.1 Comparison of the results of the algorithm in this paper and the literature［3，7，8］

从表1中可以看出，密文图像相邻像素的相关性较低，说明本文所提出的加密算法可以很好的抵抗统计攻击。

3.2.3 信息熵分析

信息熵是一种无序的、不可预测的不确定性度量。为了计算信息源的信息熵（），则有：

式中：（s）为信号s的概率；是信号源的总数。

对于一个具有256个灰度级的加密图像，理想的信息熵应为（）8。经过计算得到的密文图像的信息熵值见表1，可以看出密文图像的熵非常接近理论值8，说明本文加密算法可以很好地抵御信息熵攻击。

图7 加密图像相关性Fig.7 Encrypted image correlation

3.3 敏感性分析

加密算法应能满足密钥的敏感性，这样才能在一定程度上保证加密系统可以有效抵抗差分攻击。

3.3.1 明文敏感性分析

良好的加密系统，应该确保对明文图像的任何微小改变都会导致加密图像的显著差异，即明文敏感性。 通过计算（像素数变化率）和（归一平均变化强度）来衡量明文敏感性。

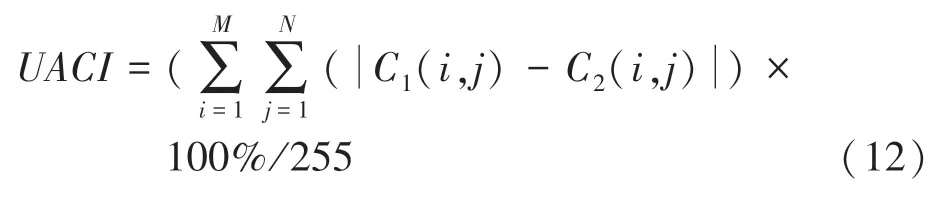
其中，、分别为图像的行和列；、分别表示密文图像和明文图像发生微小变化后的密文图像；函数用来比较两个数值是否相同。

当（，）（，）时（（，），（，））0，否则（（，），（，））1。越接近理想值09961，说明密文对明文的敏感性越好，而越接近理想值03446，说明加密算法抵抗差分攻击的能力越强。

3.3.2 密钥敏感性分析

密钥敏感性是指当密钥发生微小变化时，得到的密文图像也会引起很大变化。

以图5（b）的加密图像为例，图8给出了密钥微小变化时的仿真实验结果。其中，图8（a）和图8（b）分别是密钥取（，）（023410，0128）和（，）（0234，012810）的密文图像。 由此可见，即使密钥发生微小变化，也会生成完全不同的加密图像，证明该加密算法的密钥，即使存在微小的差异也不能正确解密图像。

图8 密钥敏感性分析Fig.8 Key Sensitivity Analysis

4 结束语

本文设计了一种Logistic和Sine映射的非线性组合Logistic-Sine混沌映射，通过Logistic-Sine映射的分岔图、Lyapunov指数变化图对其混沌性能进行了分析。结果表明，该算法具有良好的动态特性，适合应用于图像加密中。此外，比特重组方法也提高了加密效率。将Logistic-Sine映射与比特重组相结合，设计的图像加密方案，通过一系列安全性分析，表明该算法是安全可靠的图像加密算法。

目前，本文仅对标准256×256的Lena灰度图像进行了仿真实验和相关安全性分析，后续工作考虑进一步将加密方案推广到对彩色图像的研究上，同时考虑本文加解密算法能否进一步优化，以期获得更好的加密性能。