基于GSO-Kmeans的沥青路面裂缝分割算法研究
2022-05-05李显培盛文达任宜青
林 涛,李显培,盛文达,任宜青,张 玮,孙 梦
(长安大学 工程机械学院,西安 710064)
0 引 言
在社会经济和交通运输行业不断发展的情况下,许多早期修建的沥青路面出现了各种病害情况,而裂缝作为常见路表缺陷之一,不仅对道路的质量和使用寿命产生影响,还会对交通安全产生威胁。因此,研究沥青路面裂缝分割技术,对路面安全监管和养护管理具有十分重要的价值。
早期的路面裂缝检测方式一般是以人工巡检为主,存在着效率低、成本高和安全隐患等问题,而图像处理分析技术的应用,可以很好的解决这些问题。近年来,很多研究人员提出了各种技术来进行裂缝提取。邵闯等针对传统的阈值分割法难以实时分割裂缝的问题,提出了一种基于混合粒子群优化的路面裂缝图像阈值分割方法,利用该算法可以减少运算时间,提高路面裂缝分割效率;韦春桃等针对路面裂缝检测中存在噪声干扰等情况,设计了一种基于自适应阈值的裂缝自动检测方法,解决某些裂缝边缘和背景差异不明显,导致裂缝检测困难的问题,使得路面裂缝的检测结果精度得到了提高;刘晟提出了一种优化过的局部阈值分割技术,对裂缝图像进行裂缝骨架提取,可以很好的从阴影背景中提取出路面裂缝;瞿中等针对目前的裂缝检测方法,对不同环境下采集的裂缝图像集检测效果鲁棒性不强的问题,采用基于结构森林的学习框架来提取裂缝边缘,结果表明该算法具有很高的裂缝提取精确度。刘丰年等提出一种相关特征约束的分水岭分割算法,该算法分割出的路面裂缝图像准确清晰,有效降低了过分割现象;李鹏等提出了一种结合聚类和区域生长算法的路面裂缝分割算法,该算法识别准确度高、性能稳定,可以很好的解决非均匀背景情况下,裂缝分割的抗噪性低的问题。
在使用K-means聚类算法对裂缝图像进行分割时,初始聚类中心的位置很大程度上影响着Kmeans算法聚类结果的优劣程度,可能导致聚类达到收敛的迭代次数较长,抗噪性较弱,分割结果存在着很多随机干扰误差等问题。针对传统聚类分割方法的不足,本文结合GSO算法和K-means算法的优点,首先通过GSO算法优良的全局寻优的特点来确定初始聚类中心,然后在已确定的聚类中心基础上,使用K-means算法进行裂缝聚类,提高沥青路面裂缝分割的提取精度。
1 建立模型
1.1 GSO算法
GSO(Glowworm Swarm Optimization)算法又称人工萤火虫群优化算法,是印度学者K.N.Krishnanand和D.Ghose在IEEE群体智能会议上提出的一种新的群智能优化算法,通过模拟萤火虫种群的生态过程,来完成全局搜索。GSO算法具有调节参数少,达到收敛的迭代次数少等优点。其每次迭代主要包含5个阶段:萤火虫的部署(初始化)、荧光素更新阶段、移动概率计算阶段、位置更新阶段、邻域范围更新阶段。
1.1.1 初始化
首先模拟萤火虫种群。假设种群有只萤火虫,随机分布在目标区域内,每只萤火虫都有初始荧光素值(表征萤火虫的亮度)、动态决策域、初始步长、领域阈值n、荧光素挥发系数、荧光素更新因子(适应度提取比例)、动态决策域更新率(邻域变化率)、萤火虫感知域r、迭代次数。
1.1.2 更新荧光素值
在下一次迭代之前,每只萤火虫的荧光素值会随着迭代次数发生变化,其变化方式如式(1):
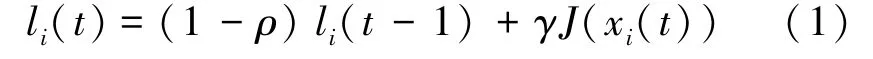
其中,在第次迭代时,l()代表了萤火虫的亮度,(x())表示萤火虫的适应度值。
1.1.3 寻找萤火虫的邻居每次迭代时,萤火虫都会在决策域半径内寻找邻居,然后组成集合。萤火虫在时刻的邻居集合N()为式(2):
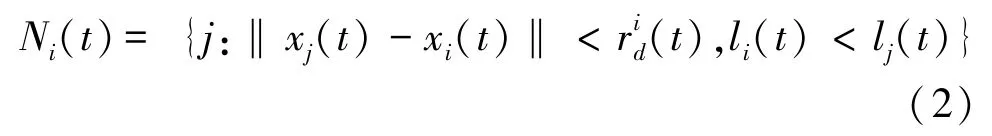
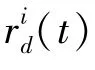
1.1.4 确定萤火虫动作移动方向
萤火虫在邻居集合N()中选择一只萤火虫,集合内每只萤火虫都有被选中的可能。选中概率如式(3):
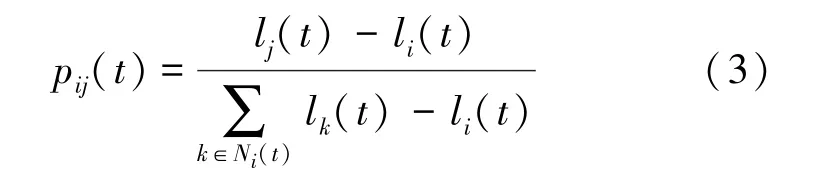
1.1.5 新萤火虫的位置
每次迭代时,萤火虫的位置变化为式(4):
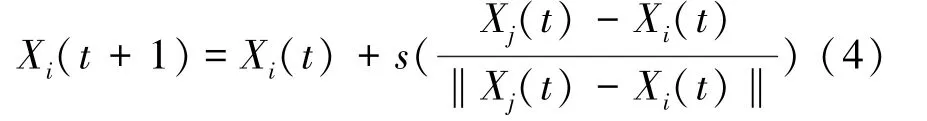
1.1.6 更新动态决策域
每次迭代完后,决策域半径可利用以下公式进行更新:
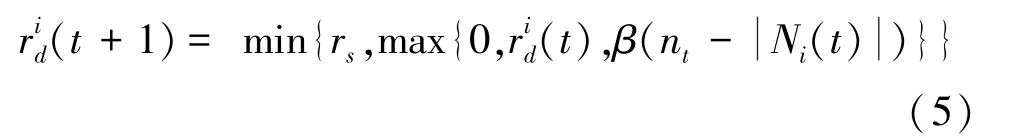
1.2 K-means聚类算法
通常情况下,K-means算法是通过个体间相似程度的判断,将多个对象分为个簇。传统K-means算法经过不停的迭代寻找最优解,通过每簇对象到各自对应簇中心的距离误差控制迭代的停止,如式(6):
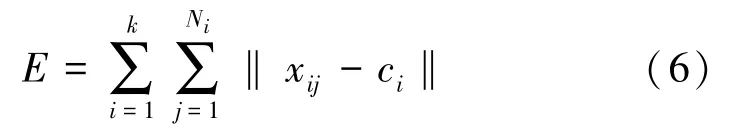
式中:x为第簇的第个样本;N为第簇的样本个数;c为第簇的聚类中心;为聚类簇的数目。
由于每次迭代各簇中心c都会不停变化,其计算形式如下:
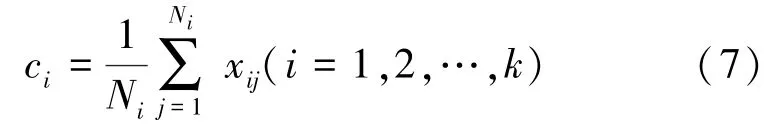
1.3 基于GSO-KMeans快速图像分割算法模型
在对裂缝图像进行分割时,最终确定的分割阈值的选取至关重要,本文算法采用基于RGB的灰度等级为的沥青路面裂缝图像,每个像素灰度的取值为[0,1,…,1]。首先,利用GSO算法良好的全局搜索能力确定初始聚类中心,在GSO算法达到收敛时,聚类中心的像素值已经接近裂缝区域的像素灰度值;利用K-means算法对沥青路面裂缝图像进行二值化分割,提取出裂缝骨架。算法流程如图1所示,具体实现步骤为:
(1)定义初始化参数,确定分类簇数和萤火虫种群的基本参数;
(2)更新所有萤火虫亮度值和维度范围;
(3)从得到的萤火虫群体中抽取个萤火虫作为初始中心,并计算每个萤火虫到随机抽取的初始中心的差异,根据距离的大小依次将萤火虫划分到各类当中;
(4)重新计算各样本的荧光素值,寻找各类中荧光素值最大的萤火虫的相应位置;
(5)更新模型中荧光素值最大的萤火虫位置;
(6)萤火虫位置更新完成后,将各类中最亮的萤火虫位置作为k-means算法的迭代初始中心;
(7)计算聚类误差平方和;
(8)更新聚类中心;
(9)判断是否达到最大迭代次数,如果没有则重复步骤(7)、(8);
(10)输出聚类中心以及聚类结果。
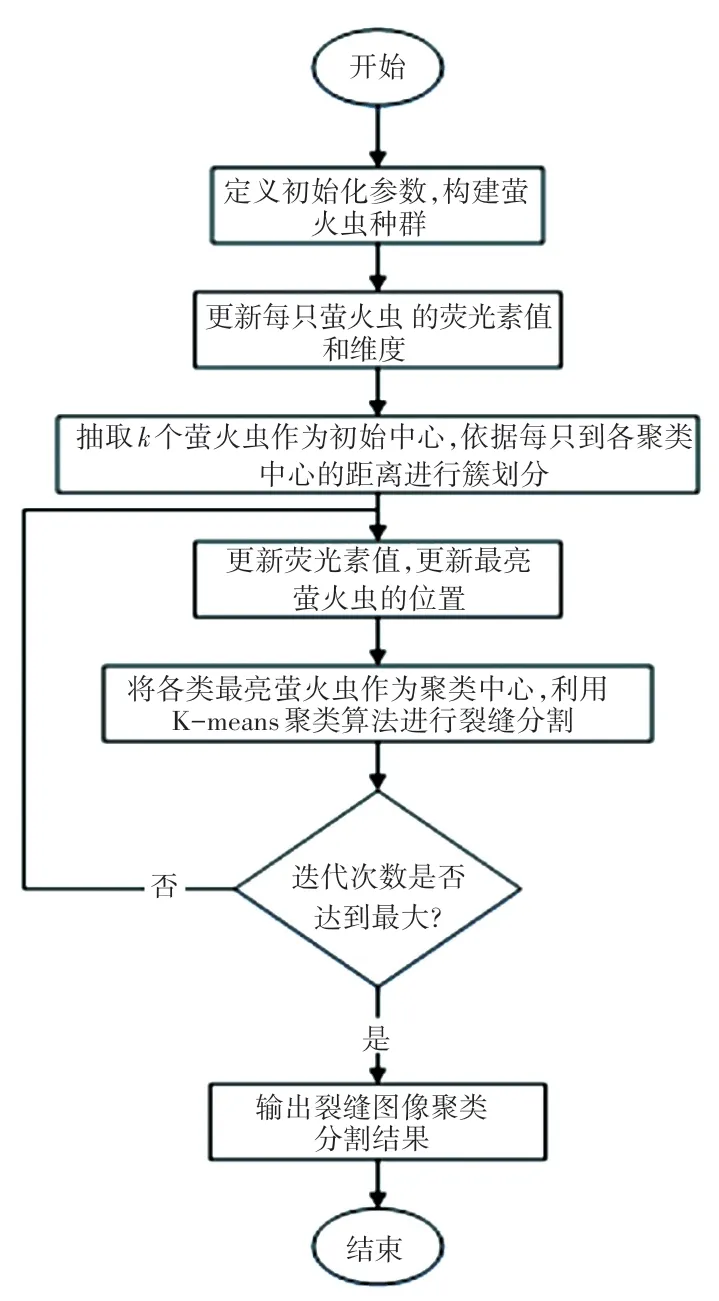
图1 GSO-Kmeans算法基本流程Fig.1 Basic flow chart of GSO-Kmeans algorithm
2 实验结果对比分析
实验图片来自手机拍摄的沥青路面裂缝照片,设定聚类簇分别为裂缝骨架和沥青路面背景。采用GSO-Kmeans聚类算法分割后的沥青路面裂缝图像如图2所示,该算法可以实现对路面裂缝图像的准确分割。

图2 GSO-Kmeans聚类前后对比Fig.2 Comparison before and after GSO-Kmeans clustering
将本文的GSO-Kmeans算法与传统的K-means聚类算法分别运用于裂缝分割,分割结果如图3所示。经过实验测试,各运行30次取平均值得到的数据,证明GSO-Kmeans聚类算法分割结果对噪声的抗干扰性比较强,且收敛时的迭代次数较少,算法收敛时间更短,具体数据结果见表1。
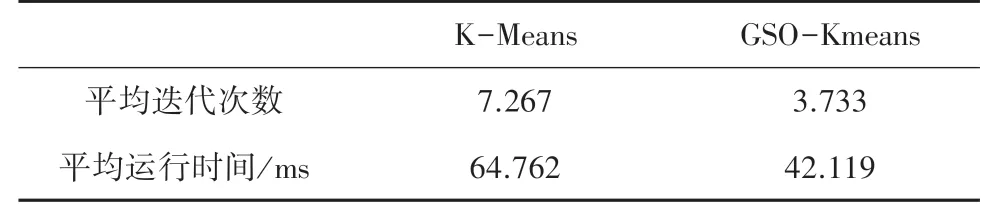
表1 算法迭代次数与运行时间对比Tab.1 Comparison of algorithm iteration times and target running time
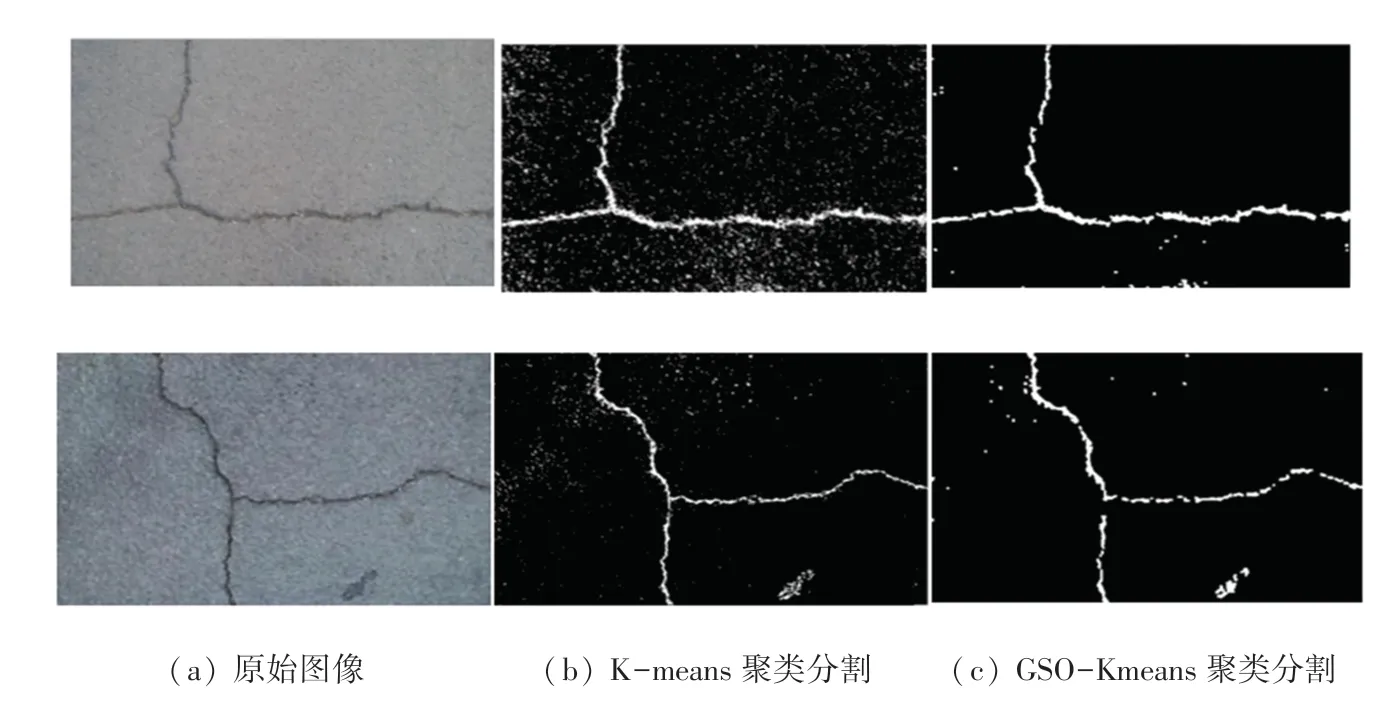
图3 路面裂缝分割试验对比Fig.3 Comparison of pavement crack segmentation test
3 结束语
传统的K-means聚类算法在应用于图像分割时,聚类中心的随机选取存在着算法迭代次数多,收敛时间长的问题。本文提出了一种结合人工萤火虫群优化算法与K-means聚类算法用于裂缝图像分割。该算法在初始化聚类中心之前,利用人工萤火虫群优化算法的全局寻优能力,快速逼近全局最优的聚类中心,然后在此基础上使用K-means聚类分割图像。将本文算法和传统的K-means聚类算法进行对比试验,结果表明本文算法可以很好地分割出裂缝骨架,提高K-means算法的抗干扰性,减少达到收敛的迭代次数,保证了沥青路面裂缝分割结果的准确性。
