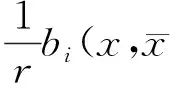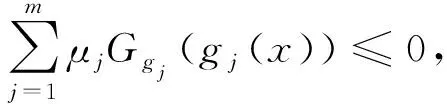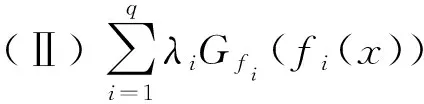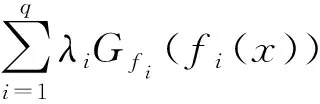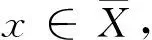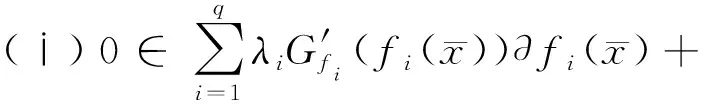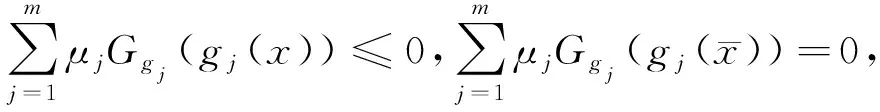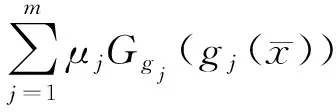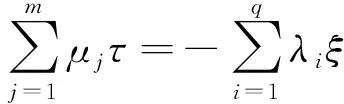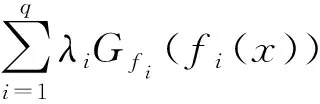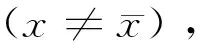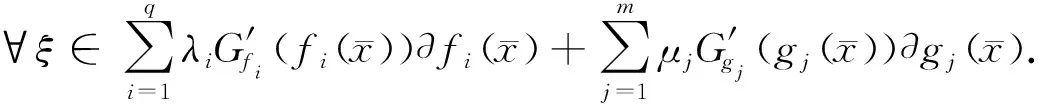G-B-(p-r-α)不变凸多目标规划的最优性条件
2022-04-30李向有刘靖雯
江 柳, 李向有, 刘靖雯
( 延安大学 数学与计算机科学学院,陕西 延安 716000)
利用广义凸函数推理最优性理论一直以来都是诸多学者关注的热门研究内容.Antcazk[1]在2001年定义了(p-r)不变凸函数,在2003年给出了广义B-(p,r)不变凸函数[2]并用新定义的函数研究了相应的数学规划问题.随后大量学者在此基础上讨论了B-(p,r)不变凸规划的最优性条件以及鞍点问题[3—5]等,李向有、张庆祥[6—7]定义了B-(p,r,α)不变凸函数,并讨论了其最优性条件和对偶性条件.G不变凸函数[8]是凸函数的另一种推广,T.Antczak[9]用这类函数研究了多目标可微规划问题的最优性条件、对偶性条件和鞍点理论,得到了许多重要结论.Y.M.Kang[10]和Ho Jung Kim[11]把G不变凸函数推广到非可微情形,定义了非可微G不变凸函数,并且研究了相应的多目标规划问题.李向有[12]定义了(G-V,ρ)不变凸函数,并用这类函数研究了多目标规划问题的对偶性条件,得到相关结论.
本文在B-(p,r,α)不变凸函数和G不变凸函数的基础上,定义了G-B-(p,r,α)不变凸函数、G-B-(p,r,α)不变拟凸函数,并用这类函数研究多目标规划的最优性条件,得到了几个最优性充分条件.
1 基本定义

∂f(x)={ξ∈Rn:f0(x;d)≥ξΤd,∀d∈Rn}.
下列不等式在全文成立:对于任意x,y∈Rn,
x≤y⟺xi≤yi;
x≤y⟺xi≤yi,但x≠y;
x 设X⊂Rn,u∈X,令f=(f1,…,fq),fi:X→Rq是定义在X上的局部Lipschitz函数,令Ifi(x),(i=1,…,k)表示fi的值,在文献[12]中作者定义了一类新的凸函数B-(p,r,α)不变凸函数,B-(p,r,α)不变拟凸函数.T.Antczak定义了非可微(G-V)不变凸函数.受此启发,我们把这两种不变凸函数进一步推广,定义G-B-(p,r,α)不变凸函数,G-B-(p,r,α)不变拟凸函数和G-B-(p,r,α)不变伪凸函数. p≠0,r≠0, p≠0,r=0, p≠0,r≠0, p=0,r≠0, p≠0,r=0, p=0,r=0, 考虑下列多目标规划问题(VP): minf(x)=(f1(x),…,fq(x)), s.t.g(x)≤0, x∈X⊆Rn, 这里fi:X→R(i=1,…,q),g:Rn→Rm,均为局部Lipschitz的实值函数,记x是(VP)的可行域. (Ⅰ)存在λ=(λ1,λ2,…,λq)>0,μ=(μ1,…,μm)≥0,使得下列结论成立: (1) 用λi乘以上面不等式并把这些不等式相加可得 (2) (3) (4) 这与 (Ⅰ)存在λ=(λ1,λ2,…,λq)>0,μ=(μ1,…,μm)≥0,使得下列结论成立: (5) 即得 (6) 因为 即 (7) (Ⅰ)存在λ=(λ1,λ2,…,λq)>0,μ=(μ1,…,μm)≥0,使得下列结论成立: (8) (Ⅰ)存在λ=(λ1,λ2,…,λq)>0,μ=(μ1,…,μm)≥0,使得下列结论成立: (9) (10) (9)式与(10)式相加得




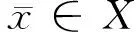


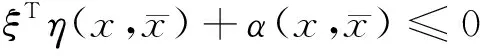
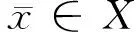
2 最优性条件