预估-校正的半隐式半拉格朗日时间积分方案及其在CMA-GFS 模式中的应用*

张红亮 沈学顺 苏 勇

中国气象局地球系统数值预报中心，北京，100081

中国气象科学研究院灾害天气国家重点实验室，北京，100081

1 引言

半隐式-半拉格朗日（SISL）方法是Robert（1981）提出，并在1985 年用于静力原始方程模式中（Robert，et al，1985）。由于SISL 方法不受Courant-Friedrichs-Lewy（CFL）的限制，在大时间步长下仍然可以保证模式的稳定和精确，很快就被应用到了业务数值天气预报模式中。欧洲中期天气预报中心（ECMWF）在1991 年发展了基于三时间层SISL 方法的业务静力谱模式（Ritchie,et al,1995），1996 年又用二时间层SISL 模式替换了三时间层SISL 模式，计算效率提高了1 倍（Temperton，et al，2001）。此外，英国气象局2005 年（Davies，et al，2005）、加拿大气象 局2002 年（Yeh，et al，2002）、中国气象局2009 年（薛纪善等，2008；陈德辉等，2006；沈学顺等，2017）都开发了基于二时间层SISL 的全球非静力格点模式。

二时间层SISL 模式假设模式格点上的空气质点在t到t+Δt的一个时间步长内沿着拉格朗日轨迹做匀速直线运动，移动速度就是轨迹中间点时刻的速度，用t和t−Δt时刻速度线性外插得到。随着模式分辨率的提高，在急流轴等风速梯度大值区时间线性外插会造成拉格朗日轨迹严重的计算误差，产生计算噪音，被认为是造成二时间层SISL 模式积分不稳定的主要原因。Hortal（2002）将匀速直线运动假定变成匀加速直线运动假定，将运动方程在拉格朗日上游点展开，保留二阶导数项，构造了稳定外插的二时间层方案（Stable extrapolation two time level scheme,SETTLS），减少了急流轴附近的虚假计算噪音。SETTLS 方案本质上仍然是时间外插方案，不能从根本上解决时间外插带来的计算不稳定问题（Durran，2004）。

二时间层SISL 模式通过引入参考大气将方程右端气压梯度力、科里奥利力和浮力项分成代表快波的线性项（L）和代表慢波的非线性项（N），因为相速度的不同，t+Δt时刻的L项采取隐式处理以增强稳定性，其他项采用显式处理。t+Δt时刻的N项也是显式表达，用t和t−Δt时刻N项线性外插得到，但在实践过程中这种线性外插会造成地形附近的计算噪音（Coiffier，et al，1987）。

为了分析解决半隐式方案中t+Δt时刻非线性项显式处理带来的计算不稳定，Cullen（2001）将预估-校正（Predictor-Corrector，简称：P-C）方法用于二时间层浅水波模式来提高模式的积分稳定性。预估-校正法一般将原来一步完成的积分分成多步计算，多步计算可以是全显式计算，比如Kurihara（1965）在预估（P 阶段）采用蛙跃格式，在校正（C 阶段）采用二阶精度的时间平均法；可以是半隐式处理，比如Kar（2012）在预估-校正的每个阶段都将一个三阶的Runge-Kutta 时间差分方案与一个重力波项二阶精度时间平均法进行组合。最早在二时间层SISL 业务模式中使用预估-校正时间积分方案的是加拿大气象局的GEM 模式（Côte，et al，1998）。后来Cullen（2001）将此方案用于ECMWF 的IFS模 式 中，Diamantakis 等（2007）在UKMO 的New Dynamical Core 上，Wood 等（2014）在ENDGAME中都使用了这个时间积分方案。

CMA-GFS 采用的是二时间层SISL 时间积分方案同样面临时间外插造成的模式积分不稳定问题。通常解决的办法是增大半隐式系数，降低模式的计算精度或减少积分时间步长，降低模式计算效率。本研究将在CMA-GFS 上发展预估-校正的半隐式半拉格朗日方案（SISL/P-C），以减少时间外插的影响提高模式的计算精度和稳定性。

2 SISL/P-C 方案

CMA-GFS 采用的二时间层SISL 通用表达式如下

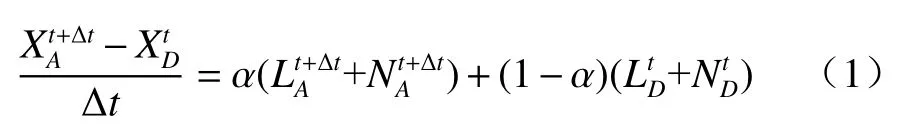
式中，X为三维速度场V、扰动无量纲气压П′、扰动位温 θ′等预报变量；L为引入参考大气之后方程组右端的线性项；N为方程组右端扣除线性项之后的残差小项，也就是非线性项；α是半隐式权重系数；A是拉格朗日轨迹到达点，也是模式格点；D是到达A点的拉格朗日上游点。

将式（1）重新写成线性方程形式

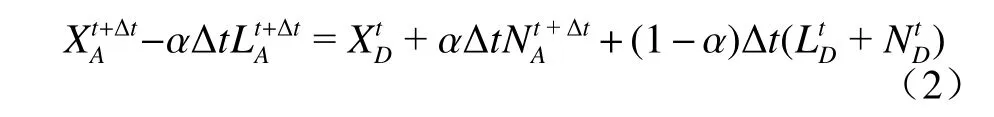
方程组（2）通过消元法得到关于t+∆t时刻П′的Helmholtz 方程组

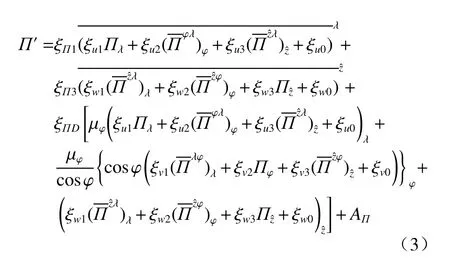
其他预报变量则可以写成关于П′的显式表达式

方程组的推导和系数表达式参见薛纪善等（2008）。系数ξu1，ξu2，ξu3，ξv1，ξv2，ξv3···等是关于∆t、α、dφ等的常数，ξu0，ξv0，ξw0，AΠ···是式（2）右端项的函数，是时间变化项。上述方程组在求解过程中是作为已知项放在方程组的右端显式表达，在传统的二时间层SISL 方案中是通过时间外插得到的

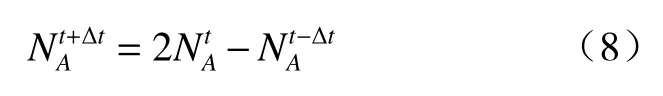
同样，半拉格朗日轨迹上的质点移动速度也是采用时间外插得到

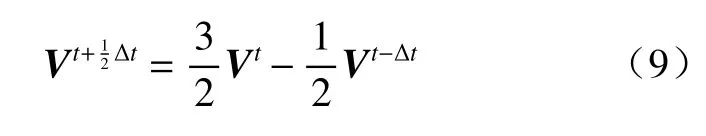
时间外插在梯度大的地方会造成计算噪音，导致模式积分不稳定。

为了减少时间外插的影响，CMA-GFS 在现有的传统二时间层SISL 方案的基础上开发了SISL/P-C 方案，式（2）通过两步来实现。

预估P：

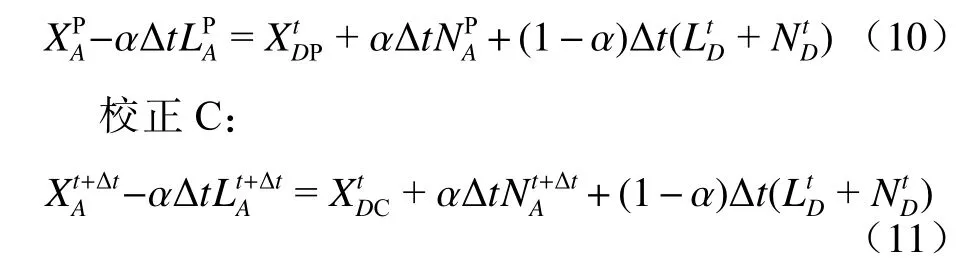
式（10）、（11）表明CMA-GFS 动力过程需要在预估P 和校正C 计算两次，也就是方程（3）—（7）要求解两次。在预估P 过程中拉格朗日轨迹中间点的速度可以用式（9）计算或者直接用到达点t时刻的速度代替（稳定性更好），估算出拉格朗日上游点的位置D；由式（8）得到。预估P 完成之后预报变量有了初猜场式（8）和（9）将变成式（12）和（13）

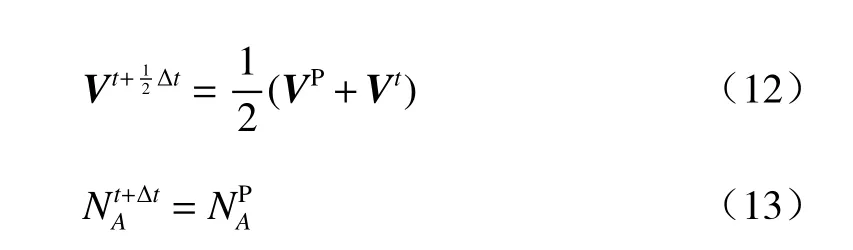
3 理想试验

DCMIP（Dynamical Core Model Intercomparison Project）（Jablonowski，et al，2008）是一个通过设计一系列理想试验比较验证模式动力框架性能的计划。文中用DCMIP 中的3 个经典理想试验：Rossby-Haurhawtz 波、地形激发的罗斯贝波和斜压波验证SISL/P-C 方案的精确性、守恒性和稳定性。

3.1 Rossby-Haurhawtz 波试验

Rossby-Haurhawtz 波是正压涡度方程的解析解，用来模拟天气尺度波动的传播和演变过程（Thuburn，et al，2000）。假设在赤道上放置4 个自西向东传播的波，理想情况下，这4个波在传播过程中会一直保持形状不发生衰减。这个试验可以展示动力框架在积分过程中的耗散、质量守恒和相速度误差等性质。具体试验设置参考Jablonowski等（2008）第4 个标准试验。模式水平分辨率1.0°，垂直不等距分为60 层，时间步长1200s，模式积分15 d 的700 hPa 高度场如图1 所示。对照试验和SISL/P-C 试验都可以模拟出4个波自西向东的传播过程，位相传播速度基本一致。在图1 中截取一个完整的波（40°S—40°N，10°—110°E），并与初始场中一个完整波（40°S—40°N，38.25°—138.25°E）进行叠加如图2 所示。与初始场相比，对照试验积分15 d 后的波形有了很大的衰减，采用SISL/P-C方案后波形与初值基本上保持一致，只是南北方向略有衰减。

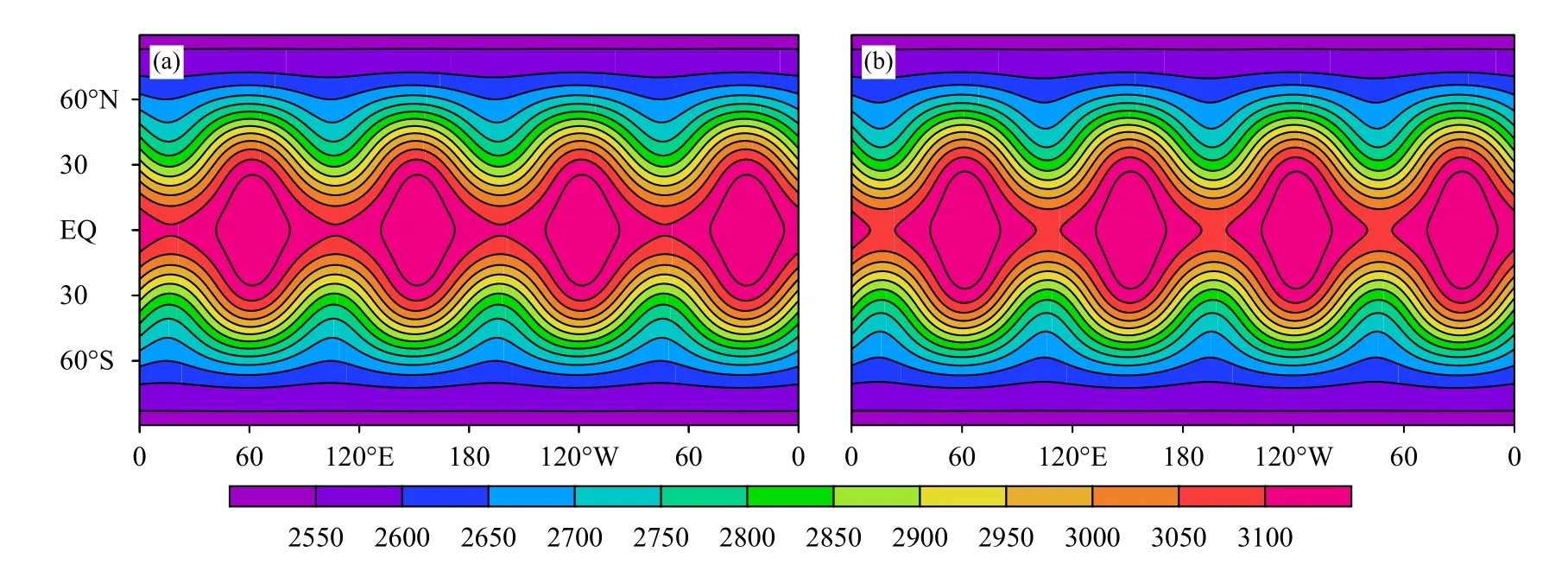
图1 Rossby-Haurhawtz 波试验积分15 d 后700 hPa 高度场（a.对照试验，b.SISL/P-C 试验；单位：gpm）Fig.1 700 hPa height in the Rossby-Haurhawtz wave experiment after 15 d of integration（a.control，b.SISL/P-C；unit：gpm）

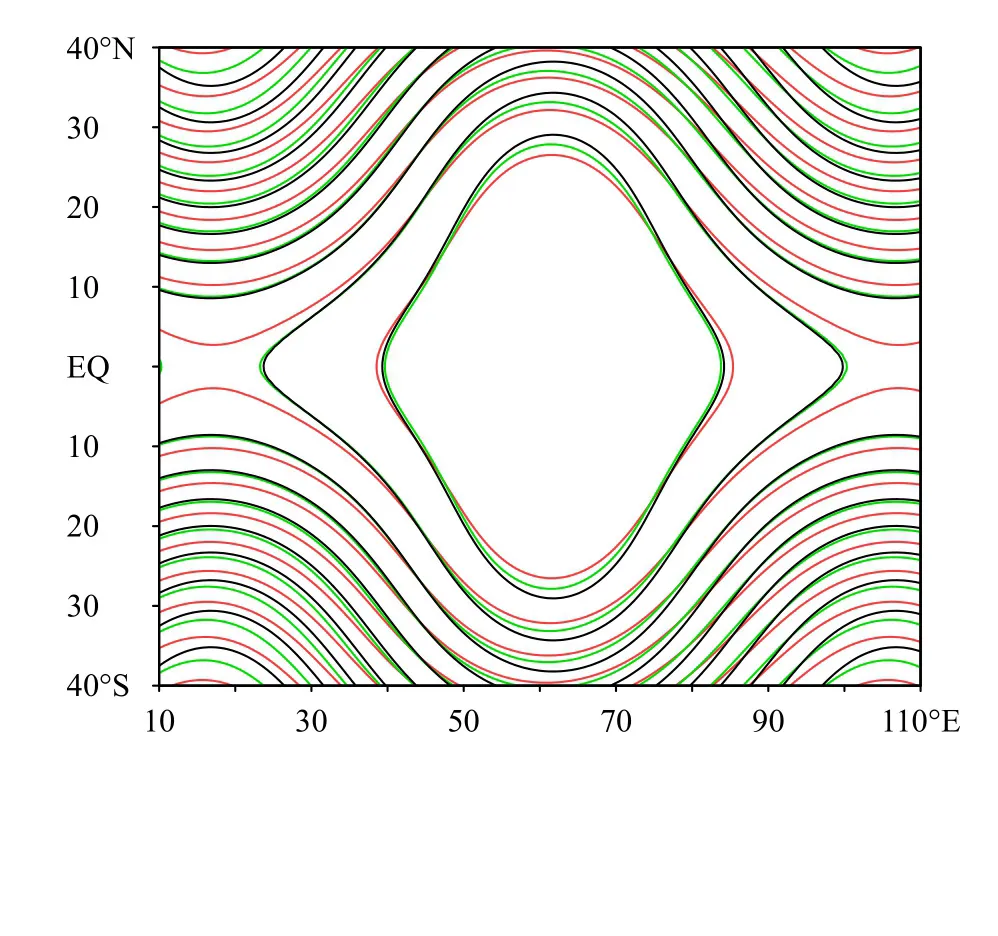
图2 Rossby-Haurhawtz 波试验 （40°S—40°N，10°—110°E）积分15 d 后700 hPa 高度场 （黑色：初始值， 红色：对照试验，绿色：SISL/P-C ）Fig.2 700 hPa height in the Rossby-Haurhawtz wave experiment（40°S—40°N，10°—110°E）after 15 d ofintegration（black：initial value，red：control，green：SISL/P-C）

3.2 地形激发的罗斯贝波

假设在北半球中纬度地区放置一个钟形地形，流经地形的平直西风气流在地形的激发下会产生罗斯贝波，本试验就是模拟罗斯贝波的产生、演变和消亡过程。具体的试验设置参照Jablonowski 等（2008）第5 个干动力框架标准试验。模式水平分辨率0.5°，垂直均匀分成60 层，每层厚400 m，时间积分步长分别为600 s 和1200 s。图3 是模式积分15 d 的700 hPa 高度场。2 个试验在时间步长分别取600 s 和1200 s 时都可以很清晰地模拟出山脉激发的罗斯贝波的激发和传播以及消亡过程。气流过山后在背风坡都形成了明显的地形强迫罗斯贝波。

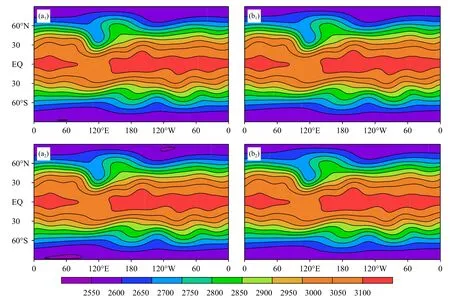
图3 地形激发的罗斯贝波传播15 d 后700 hPa 高度场（a1、a2：对照试验，b1、b2.SISL/P-C；a1、b1.1200 s，a2、b2.600 s；单位：gpm）Fig.3 700 hPa height in the mountain-induced Rossby wave experiment after 15 d of integration（a1，a2.control，b1，b2.SISL/P-C；a1，b1.1200 s，a2，b2.600 s；unit：gpm）

对照试验中模拟的山脉下游的槽、脊强度与其他模式相比较弱（苏勇等，2018）。本试验中选取该区域进一步仔细比较两组试验的差别，如图4 所示。不论时间步长取600 s 或是1200 s，SISL/P-C模拟的槽和脊强度都比对照试验加强，明显缓解了系统偏弱的问题。图5 给出了0—15 d 平均地面气压的变化。SISL/P-C 在2 组试验中经过15 d 的预报，地面气压的变化明显低于对照试验，当时间步长取600 s 时，积分15 d 后对照试验中地面气压降低了 1.13 hPa，SISL/P-C 降低0.57 hPa，是对照试验的一半；当时间步长取1200 s，积分15 d 后SISL/P-C的地面气压变化比对照试验减少0.2 hPa。

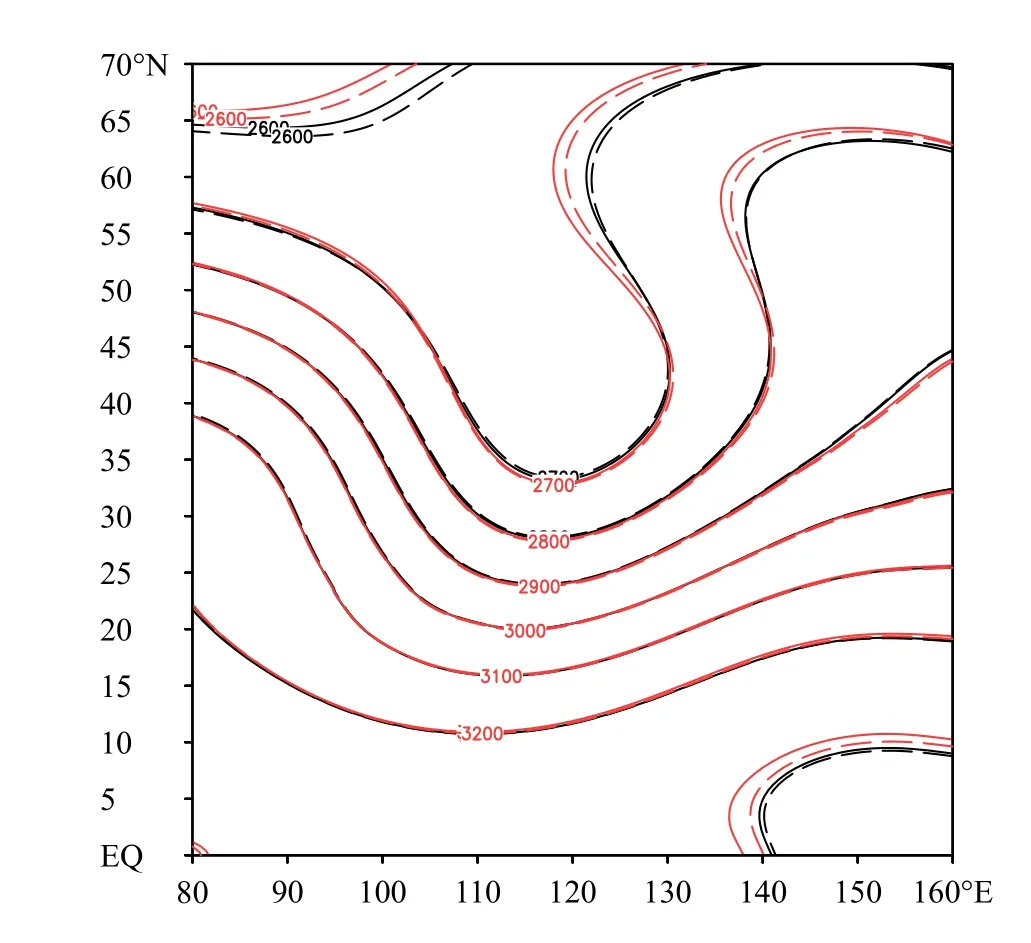
图4 地形激发的罗斯贝波传播15 d 后700 hPa（EQ—70°N，80°—160°E）高度场（实线：600 s，虚线：1200 s；黑色：对照试验，红色：SISL/P-C；单位：gpm）Fig.4 700 hPa height（EQ—70°N，80° —160°E）in the mountain-induced Rossby wave experiment after 15 d of integration（solid：600 s，dashed：1200 s；black：control，red：SISL/P-C；unit：gpm）

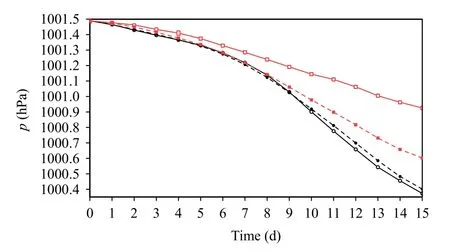
图5 地形激发的罗斯贝波传播0—15 d 平均地面气压变化（黑色：对照试验，红色：SISL/P-C；实线：600 s，虚线：1200 s；单位：hPa）Fig.5 Averaged surface pressure changes over 0—15 d in the mountain-induced Rossby wave experiment（black：control，red：SISL/P-C；solid line：600 s，dashed line：1200 s；unit：hPa）

3.3 斜压波试验

斜压波试验是在一个平直的西风气流上叠加一个扰动的纬向风场后激发出了一个短时斜压波，这个斜压波在第9 天发展最为强盛，然后逐渐衰亡。具体扰动设置参见Jablonowski 等（2008）第1 个干动力框架标准试验。模式水平分辨率0.5°，垂直采用业务60 层不均匀分层，时间步长600 s。两组试验都模拟出扰动风场的发生、发展和加强过程，如图6 所示。与Jablonowski 中T106 结果相比，积分第9 天两组试验都激发出了3 个波峰，波峰位置和强度与T106 基本一致。进一步将时间步长延长到1200 s 和1800 s，选择子区域（30°—70°N，120°E —100°W）对比3 种时间步长下第9 天850 hPa温度场，如图7 所示。对照试验在600 s 积分时间步长下波的发展最强烈，积分步长增加1 倍波的振幅已经有所衰减；增加2 倍时衰减已经非常明显。SISL/P-C 试验中3 种时间步长下第9 天的温度场还是基本上重合在一起，没有因为时间步长的增大而明显衰减，说明SISL/P-C 方案有非常好的稳定性。这也使得CMA-GFS 延长积分时间步长，提高计算效率成为可能。

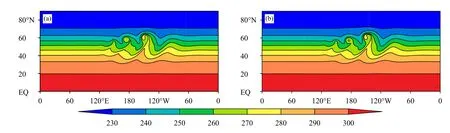
图6 斜压波试验模式积分9 天850 hPa 上的温度场（单位：K）（a.对照试验，b.SISL/P-C；单位：K）Fig.6 850 hPa temperature in the baroclinic wave experiment after 9 d of integration（a.control，b.SISL/P-C；unit：K）

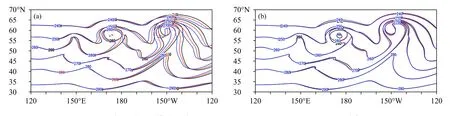
图7 斜压波试验模式积分9 天850 hPa（30—70°N，120°E —120°W）温度场（a.对照试验，b.SISL/P-C；黑色：600 s，蓝色：1200 s，红色：1800 s；单位：K）Fig.7 850 hPa temperature（30°—70°N，120°E—120°W）in the baroclinic wave experiment after 9 d of integration（a.control，b.SISL/ P-C；black：600 s，blue：1200 s，red：1800 s；unit：K）

4 实际资料试验

CMA-GFS_V3.0（苏勇等，2020）水平分辨率0.25°，垂直62 层，模式层顶位于36 km。物理过程包括长短波辐射、积云对流参数化过程、微物理降水过程、边界层和陆面过程以及地形重力波等过程（沈学顺等，2017；马占山等，2016；宫宇等，2018）。采用NCEP 的FNL（Final operational global analysis data）资料作为模式的初始场，试验时段为2018 年7 月1 日到31 日，每天12 时（世界时）开始进行8 d预报。对照试验中半隐式系数为0.72，SISL/P-C中是0.55，时间积分步长分别取300 s 和450 s。

图8 是2018 年7 月12 日72 h 预报的500 hPa高度场。图中黑色线是SISL/P-C 试验，红色线是对照试验；实线和虚线代表时间步长分别为300 s和450 s。SISL/P-C 试验中两种时间步长下预报的形势场并没有明显差别，而且与对照试验在300 s时间步长下的预报结果基本吻合。当对照试验中时间步长延长到450 s 时72 h 预报的形势场有明显衰减，这个结论与理想场试验的结果是一致的：SISL/P-C 方案是稳定的，对照试验的稳定性差。所以在0.25°的水平分辨率下对照试验的时间步长为300 s，SISL/P-C 试验的时间步长在此基础上增加到450 s。

图8 2018 年7 月12 日12 时（世界时）起报72 h 预报的500 hPa 高度场（黑色线：SISL/P-C，红色线：对照试验；实线：300 s，虚线：450 s；单位：gpm）Fig.8 500 hPa height after 72 h of integration starting from 12：00 UTC 12 July 2018（solid：300 s，dash：450 s；black：SISL/P-C，red：control；unit：gpm）

两组试验月平均的5 d 预报500 hPa 高度场的距平相关系数和预报偏差如图9 所示。SISL/PC 试验中在两组时间步长下500 hPa 高度场的距平相关系数和预报偏差没有明显区别。与对照试验相比，500 hPa 距平相关系数略有提高；预报偏差有明显改进。温度场的检验结果相同，风场的检验基本持平，没有明显改进。

图10 是SISL/P-C 预报试验的综合评分卡，分东亚、北半球、南半球、赤道4 个区域分别对风场、温度场、高度场进行检验，左列为预报时效1—8 d的距平相关系数，右列为均方根误差，红色表示正效果，绿色表示负效果，灰色为中性，箭头越大效果越显著。SISL/P-C 的时间步长与对照试验一样为300 s 时，模式的整体预报性能都有所改善，特别是均方根误差有明显降低，南半球的各个预报场以及热带地区的风场的距平相关系数也有明显提高。SISL/P-C 的时间步长提高到450 s，除了东亚和北半球地区温度场的距平相关系数有负影响，其他地区是中性偏正的影响。

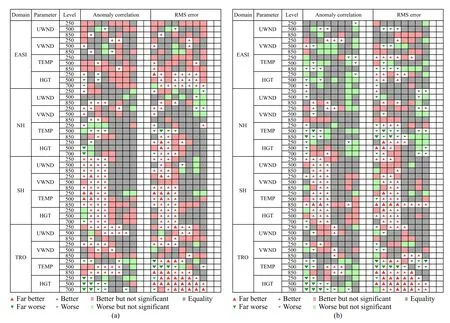
图10 SISL/P-C 预报试验的综合评分卡（a.300 s，b.450 s）Fig.10 Comprehensive scoring cards for prediction experiment of SISL/P-C（a.300 s，b.450 s）

图11 是2018 年7 月31 d 平均的全球平均海平面气压随时间的变化。图中黑色实线是对照试验的结果，8 d 预报的平均地面气压下降0.65 hPa。SISL/P-C 8 d 预报的平均地面气压与初始平均地面气压相比损失都有所减少，当时间步长与对照试验一样为300 s 时，8 d 预报平均地面气压下降0.5 hPa，比对照试验明显减少。

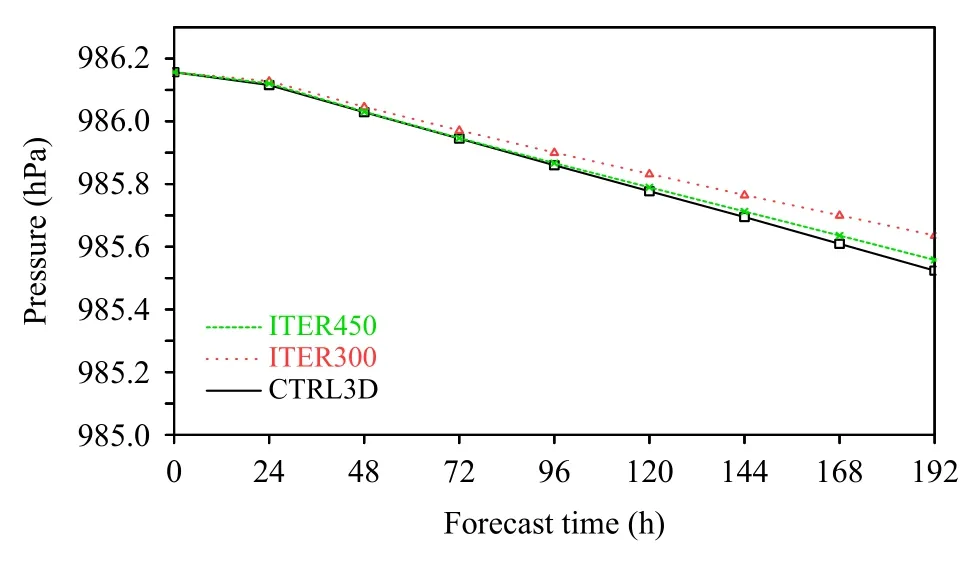
图11 2018 年7 月全球平均的海平面气压随时间的变化Fig.11 Changes of global mean sea level pressure over time in July 2018

SISL/P-C 的预估、校正过程中动力框架要积分两次，第2 次积分过程中t时刻格点上的值不再重复计算，并且将预估值作为求解Helmholtz 方程组的初猜场极大减少了方程组的余差和迭代收敛次数，在与对照试验相同的时间步长下8 d 预报时间仅增加了40%。由于SISL/P-C 方案有非常好的计算稳定性，0.25°分辨率下时间步长可以延长50%到450 s，模式预报结果和效果仍然是稳定的，8 d 预报时间减少20%，计算效率明显提高。

5 结论与讨论

为了减少二时间层SISL 方案中时间外插对预报稳定性和精度的影响，在CMA-GFS_V3.0 的基础上发展了SISL/P-C 方案。SISL/P-C 中动力框架要完整地计算两次，为了最大限度地保证预估P 过程的精度，预估P 过程与CMA-GFS_V3.0 一致；在校正C 过程中原来需要时间外插的拉格朗日上游点移动速度根据预估值可以线性内插得到，需要显式处理的t+∆t时刻非线性项也可以根据预估值直接计算。

文中用3 个经典理想试验（Rossby-Haurhawtz波、地形激发的罗斯贝波和斜压波试验）证明了相比于对照试验，SISL/P-C 的波形衰减明显减少，计算精度显著提高。将积分时间步长延长2—3 倍后SISL/P-C 长时间积分后波的形状、强度和移动速度仍然保持不变，模式的稳定性得到了很大的提高，这也为实际预报中增大积分步长提高计算效率提供了支持和保障。

本研究也进行了1 个月的实际资料的对比试验，SISL/P-C 的总体预报效果优于对照试验。不同积分步长下SISL/P-C 72 h 预报的500 hPa 高度场和温度场基本上是一样的，对照试验随着时间步长的增大有明显衰减，新方案提高了模式的积分稳定性。

基于SISL/P-C 方案等改进生成的CMA-GFS_V3.1 四维变分同化系统2020 年汛期前正式业务运行。模式水平分辨率0.25 °,垂直不等距分为87 层，模式层顶延伸到0.1 hPa，时间积分步长由300 s 提高到450 s。

目前，开发的SISL/P-C 方案是CMA-GFS_V3.1动力框架的计算方案。Wood 等（2014）和陈子通等（2020）在预估-校正方案中增加了物理过程的影响。采用SISL/P-C 方案后CMA-GFS 动力框架的半隐式系数由0.72 减少到0.55，动力框架近于二阶计算精度，但是物理过程和动力框架的耦合还是一阶精度，所以进一步提高CMA-GFS_V3.1 的动力-物理耦合精度将是未来的工作重点。