地震相控约束下的储层高精度定量预测方法——以曲塘次凹阜三上亚段为例

王东坤，谢英刚，张军林，逄建东，葛 岩

（中海油能源发展股份有限公司工程技术分公司，天津 300457）

曲塘次凹位于苏北盆地东台坳陷中的海安凹陷西南部（图1），南北部分别与泰州低凸起、通扬隆起相邻，整体呈北东向展布，内部地层沉积构造呈北深南浅、北断南超、北厚南薄的特点[1]。曲塘次凹西斜坡在阜三段发育的油藏类型为岩性油藏，储层沉积类型为滨浅湖滩坝砂体，沉积规律复杂，砂体平面及垂向分布非均质性较强，此外主力砂体厚度小于5 m，地震资料主频较低（25 Hz），常规储层预测方法无法精细刻画薄砂体。

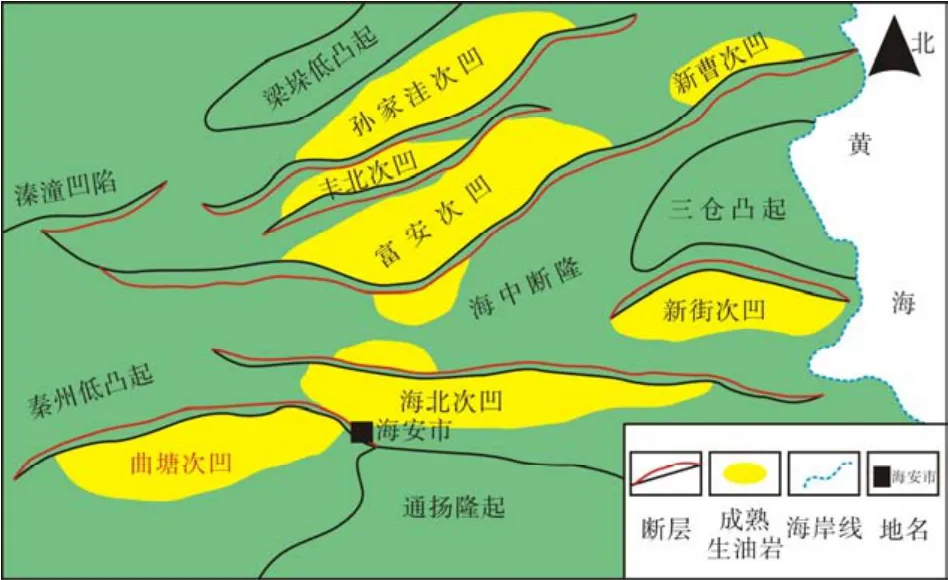
图1 曲塘次凹构造位置

薄储层的定量预测一直是地球物理技术人员研究的难点，目前薄储层定量预测的主要技术方法是叠前、叠后随机反演。杨文采（1995）、张厚柱等（1995）、张繁昌等（1997）采用模拟退火、人工神经网络、混沌反演等一系列非线性反演方法实现了对薄储层定量描述[2–4]；Marfurt和Kirlin在2001年运用谱分解方法在墨西哥湾地区实现了薄储层的定量预测[5]；王香文等（2012）、闵小刚等（2015）、王秀玲等（2019）、孙思敏等（2019）利用基于贝叶斯判别的地质统计学反演方法实现了对薄储层的定量体的预测精度不理想。

针对阜三段储层精细刻画存在的难点，在研究区井控较低的情况下，深度挖掘有效地震信息，基于主成分分析的地震相分析技术建立地震属性与沉积微相的相关关系，获取滩坝砂体平面展布变程、方向、规模等关键表征参数，将表征参数用于地质统计学反演中变差函数的分析。

变差函数反映不同沉积微相的空间变化特征，将沉积模式和地质模型引入反演中，对后期反演进行“相控”约束。弱化随机反演井间结果的不确定性，高分辨率地质统计学反演可以识别和预预测[6–9]；高君等（2017）运用基于地震波形约束的波形指示反演，实现了对薄储层的定量预测[10]。这些研究成果均较好地应用于薄储层的勘探开发工作，但是随机反演方法对井位要求较高，井控不足时井间随机性较强，尤其是针对空间分布复杂的滩坝砂测薄储层，最终实现对滩坝薄砂体的高精度定量表征。

1 沉积相模式

研究区阜三段以细粒沉积为主，岩心颜色以灰色、浅灰绿色、灰黑色等还原色为主，粒度概率累积曲线呈现传统两段式及冲洗两段式的形态特征，属于滨浅湖沉积亚相，为洪水期湖岸线以下、浪基面以上的浅水地带，包括砂滩、坝砂、滨浅湖泥三种沉积微相（图2）。

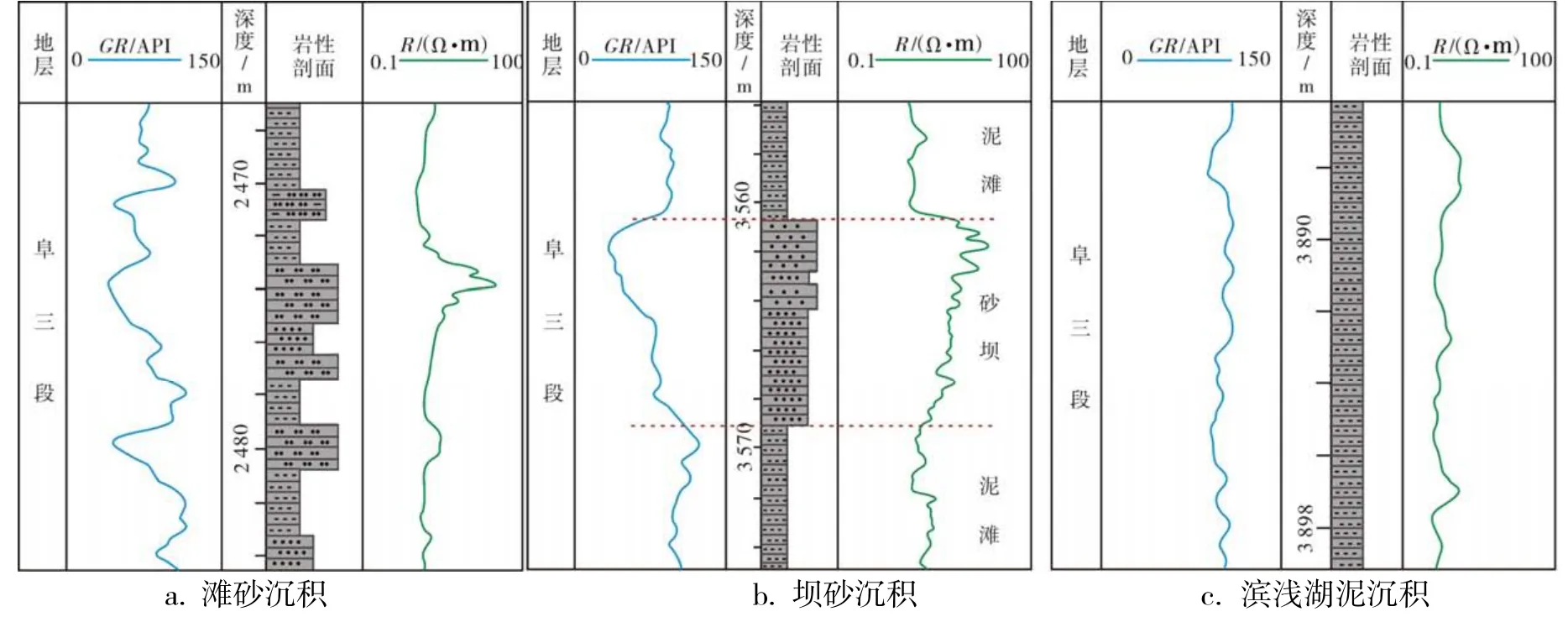
图2 阜三段典型测井相标志

砂体沉积类型主要发育滩砂、坝砂微相，波浪和沿岸流是滩坝形成的主要控制因素，坝砂多呈条带状平行湖岸线分布，在平面上包围于条带状或席状展布的滩砂之中。岩性以浅灰绿色细–粉砂岩、灰黑色泥质粉砂岩为主，沉积物呈现细粒、反旋回特征，沉积构造以浪成交错层理、波状层理等沉积构造为主，偶有泥岩撕裂及搅浑构造发育，具有明显的双向水流作用，伴随偶发的风暴沉积。生物钻孔在阜三段基本全段显著发育，沉积环境相对静水环境，在伽马曲线上主要表现为漏斗型、指状漏斗型形态[11]。

2 主成分分析地震相

2.1 基本原理

地震道波组、波形特征是地下岩石岩性、物性在空间上的变化综合响应，通过分析地震波组特征（振幅强度、频率、相位、组合形态等）研究储层空间分布及物性特征。Naaman Keskes（1982）最早提出地震道波形分类的分析方法，此后SIBILLE（1984）对地震道波形分类基本原理进行系统化阐述，即根据地震波反射界面中同相轴排列组合的多种属性（杂乱、波状、平行和复合波形），采用多元统计方法进行归类，并将其初步用于地震相分析研究[12]。

神经网络技术利用人工智能，通过基于自适应试验和误差处理方法，对单一或多种属性体的相邻地震道波形进行数理统计分类。对地震波组特征按照相关性进行分类排列建立模型道，然后将模型道应用于整个数据体，进而实现目的层的地震相划分（图3）。神经网络技术具有自组织、自适应性以及聚类功能， 在此基础之上结合钻井地质分析，可以实现隐蔽油气藏的有效勘探[13–14]。

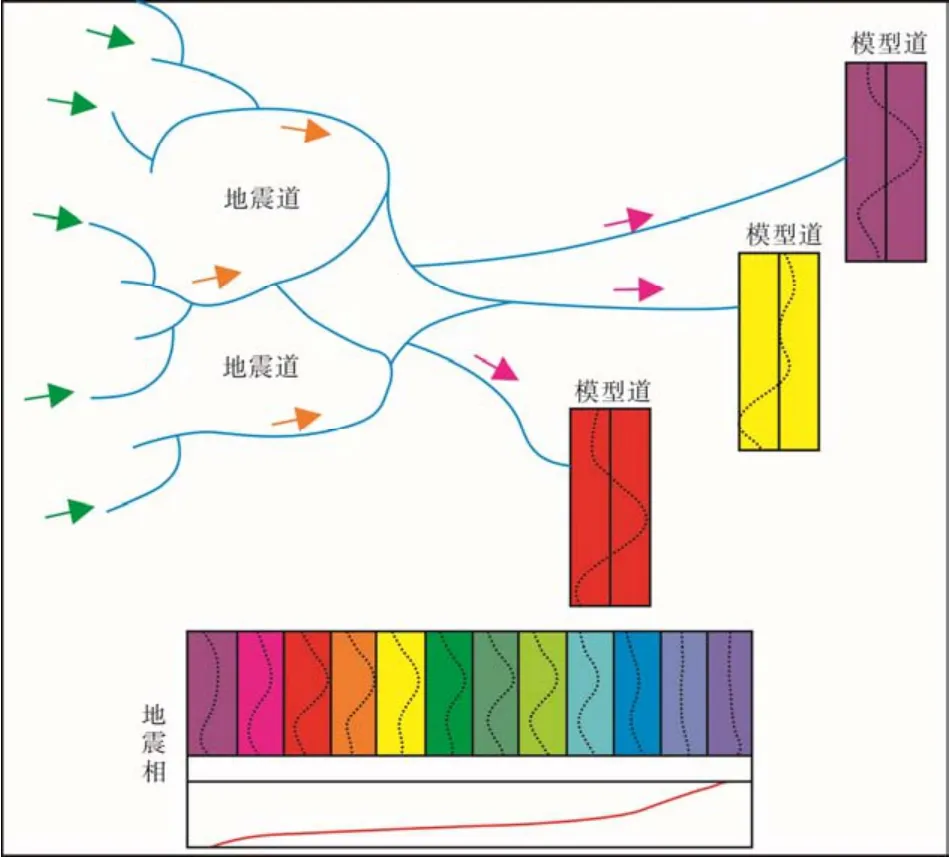
图3 神经网络波形聚类原理

由地震数据可以获得成十上百种地震属性，储层参数与地震属性之间存在多维–多维的对应关系（一种岩石特性的变化对多种地震属性有影响，一种地震属性反映岩性、孔隙度、流体成分、压力等多种性质的变化）。神经网络技术对多属性体进行分类的过程中，需要对地震数据进行压缩分析，尽可能保持地震有效信息，滤除非地质因素所引起的噪音信息。PCA法是一种利用降维思想，即把多指标简化为不相关的几个综合指标的一种多元统计分析方法[15–16]。对多维数据的交会得到多属性数据的共同趋势即主组份方向，主组分数据的正交方向为次级数据延展方向，将组份中对数据延展方向贡献不大的组分（主要是冗余数据或噪声）剔除，突出主组分数据，从而达到简化数据的目的（图4），然后利用模糊算法耦合优选出不同量纲的地震属性体，最终实现利用神经网络技术进行聚类划分地震相。

图4 PCA原理

2.2 研究流程

PCA法地震相研究过程中（图5），影响地震相预测精度的重要参数主要包括多种地震属性体、主成分、分类数、迭代次数。以上参数选取遵循以下原则：①分类时窗为垂向包含目的砂体的变时窗/等时窗（一般至少要大于半个相位子波长度，小于150 ms，时窗太大对目的砂体不聚焦，会对地震相解释带来干扰）；②主成分数据的选择主要基于累计贡献率，主成分累计贡献率大于90%便可认为有效（主成分数量不可过多）；③分类数的选取取决于对研究区沉积特征和地震数据的认识程度（若分类数过大、细节过多则无法形成趋势性的认识，分类数过小则结果过于模糊而忽略掉关键地震相类型。在实际应用中，根据地震数据波形特征复杂程度和目的层时窗大小，一般分类数为5～10）；④根据经验，自适应神经网络算法经过10次迭代计算可实现收敛到最终结果的80%左右，经l0～20次迭代计算就可确保得到较好的分类结果，一般选用 20～ 40次迭代确保得到最佳分类结果。

经过主成分分析数据压缩和神经网络自适应聚类判别，实现地震道、多属性数据体以及变时窗/等时窗层段内的地震相自动划分（图5），地震相聚类研究效率更快、储层预测精度更高。

图5 PCA地震相流程

2.2.1 获取多种地震属性体

根据地质研究的需要，计算了24种复合地震道属性数据体、3种地震道的几何属性体、地震分频属性的信号振幅和信号包络等10种地震分频属性体，总计提取属性体37种。在构造解释层位的基础上，根据阜三段上亚段层段主力砂体垂向位置，以阜三段顶往下开10 ms为顶，以阜三段顶往下开30 ms为底，提取目的层段地震属性（图6）。

图6 过井地震剖面

2.2.2 PCA分析

利用阜三段上亚段顶底的层位建立研究目的段。选择多种属性体对目的层进行降维处理，经PCA分析之后提取前4个主成分（均方根振幅、吸收因子、最大振幅、分频地震属性），累计贡献率达到0.913 36（表1），将这 4个主成分作为神经网络训练的地震属性数据输入部分进行聚类分析。

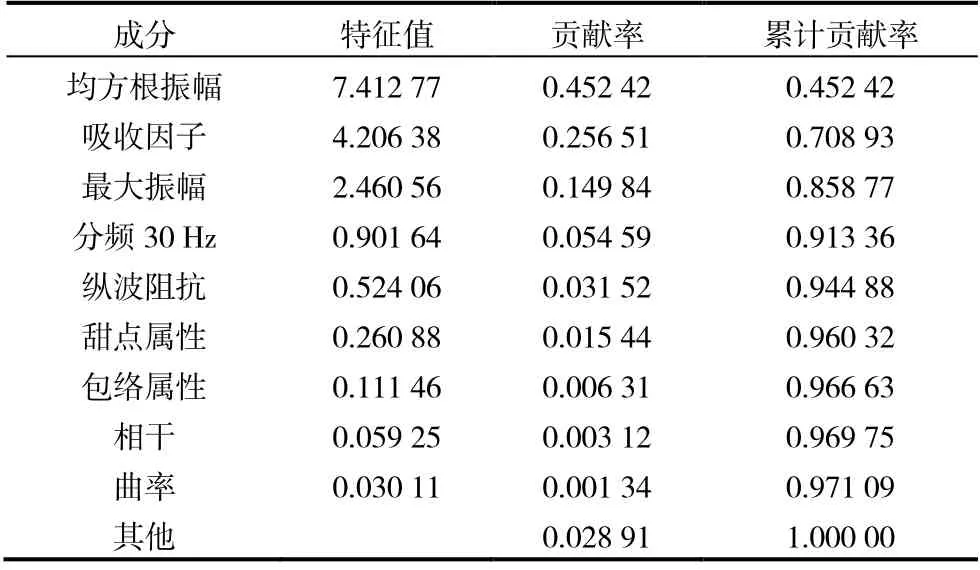
表1 PCA分析结果

2.2.3 分类数的选取

分类数是重要的经验参数，是指在目的层段内确定的模型道的个数，合理的分类数需要结合实际地质情况多次估算（一般大于3次）得到。合理选取分类数十分重要，分类数过大则细节过多，无法形成趋势性的认识；分类数过小则可能会模糊掉关键地震相类型。通过对相邻道组的波形进行反复迭代相关分析，建立11类模型道，利用模型道对地震数据进行分类。

2.2.4 迭代次数

根据经验，经过神经网络算法至少10次迭代计算后就可以得到较好的收敛效果，确定的模型道类型数比较合理，本次研究选用20次迭代，可以保证最佳的收敛效果。

结合地震相分类结果、井上钻探结果以及目的层的相模式，实现对阜三段上亚段砂体地震相及沉积微相的定性刻画和分类（图7）。研究区目的层滩砂呈条带状、席状分布，坝砂砂体呈点状、窄条带状分布，暖色调区域（1～4）为坝砂主体发育区，砂体发育比较厚，次暖色调区域（5～8）为滩砂、坝砂主体发育区，其他区域（9、10、11）滩砂为主，砂体较薄，X20井北部为有利区。

图7 阜三上亚段地震相

3 相控统计学反演

地质统计学反演最早由 Hass等（1994）提出，Dubrule 等（1998）和 Rothman（1998）加以发展，Torres-Verdin 等（1999）将其完善[7]。其算法由最初的序贯指示和序贯高斯算法发展到基于马尔科夫链–蒙特卡罗算法，后者具有全局寻优的特点，综合了统计模拟与确定性反演的优势；通过综合地震、测井和地质资料，将地质认识加入反演过程中可提高地震资料识别储层的能力，拓宽地震数据频带。在提高地震纵向高分辨率的过程中并未降低地震横向分辨率，具有确定性反演无法比拟的识别薄层的高分辨能力[17–18]。

地质统计学反演技术以地震数据为软约束，以测井数据为硬约束条件，在地震尺度上，通过协克里金将其与弹性参数进行融合；在测井尺度上，利用变差函数统计不同沉积微相的空间变化规律；在层序地层格架控制下，通过线性加权，实现在远离井的地方融合地震趋势数据来校正插值。地质统计学反演中，地质先验信息主要由概率密度函数（PDF）和变差函数来确定，二者分别描述了离散或连续属性在空间的概率分布情况及空间展布特征随距离的变化情况。

在对地震资料和测井资料优化处理的基础上，利用已钻井测井解释的砂泥岩性数据（图8），统计岩性比例、不同岩性波阻抗的数值分布特征、各岩性垂向变差。统计显示，目的层段砂岩和泥岩的比例分别是0.35和0.65，泥岩段纵波阻抗值为6.3×106～9.5×106g/（cm3·m·s-1），波阻抗峰值为7.2×106g/（cm3·m·s-1），砂岩段纵波阻抗为7.9×106～1.1×106g/（cm3·m·s-1），波阻抗峰值为8.8×106g/（cm3·m·s-1），纵波阻抗可以很好地区分储层。统计显示，目的层单砂体厚度小于5 m，目的层速度砂岩速度均值取3 200 m/s，砂岩垂向变差取1 ms较为合适；然后以地震相结果建立的地质模式为指导，通过量取地震相图中砂体长宽数据来确定各岩性平面变差函数（表2），最后结合地震相和统计学反演结果，多次迭代精细分析和调试地震信噪比参数（经测试21 db最合适），从而达到降低井间结果随机性的目的，最终达到地震相、沉积相与统计学反演结果三者的最佳匹配与耦合。

表2 变差函数

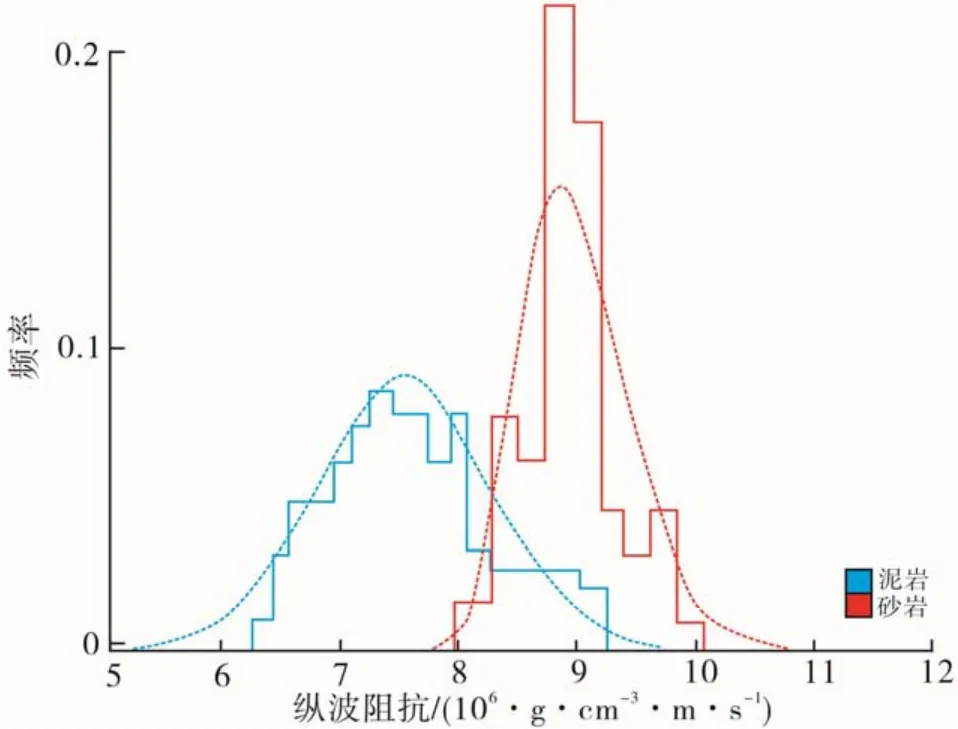
图8 多井储层敏感参数交会

在研究区共搜集了8口井的钻井资料，为保证反演效果，以X20H1井作为检验井，其他井均参与反演。从统计学反演砂体厚度分布看出（图9），未相控约束的结果虽然井上砂体厚度与预测深度厚度相吻合，但是井点处井约束导致的“牛眼”现象严重，砂体展布规律不明显，井间结果不确定性强；经相控约束的预测结果不仅和井上实钻厚度相吻合，而且砂体平面展布更为合理。阜三段上亚段砂体整体呈环状展布，为滩坝沉积模式，其中滩砂呈带状、席状分布，厚度为2～4 m；坝砂砂体呈点状、窄条带状分布，在平面上包围于滩砂之中，厚度为4～7 m，坝砂砂体间由滩砂过渡，砂体厚度减薄、连通性或物性变差，岩性遮挡控制油藏边界。从剖面上看（图10），相控统计学反演结果可有效识别出井上1～2 m的单砂体，精度高。X20H1水平井作为盲井未参与反演，水平段砂体预测结果与实钻结果吻合度为94%，实现了对研究区滩砂、坝砂体平面和垂向分布的高精度定量预测。

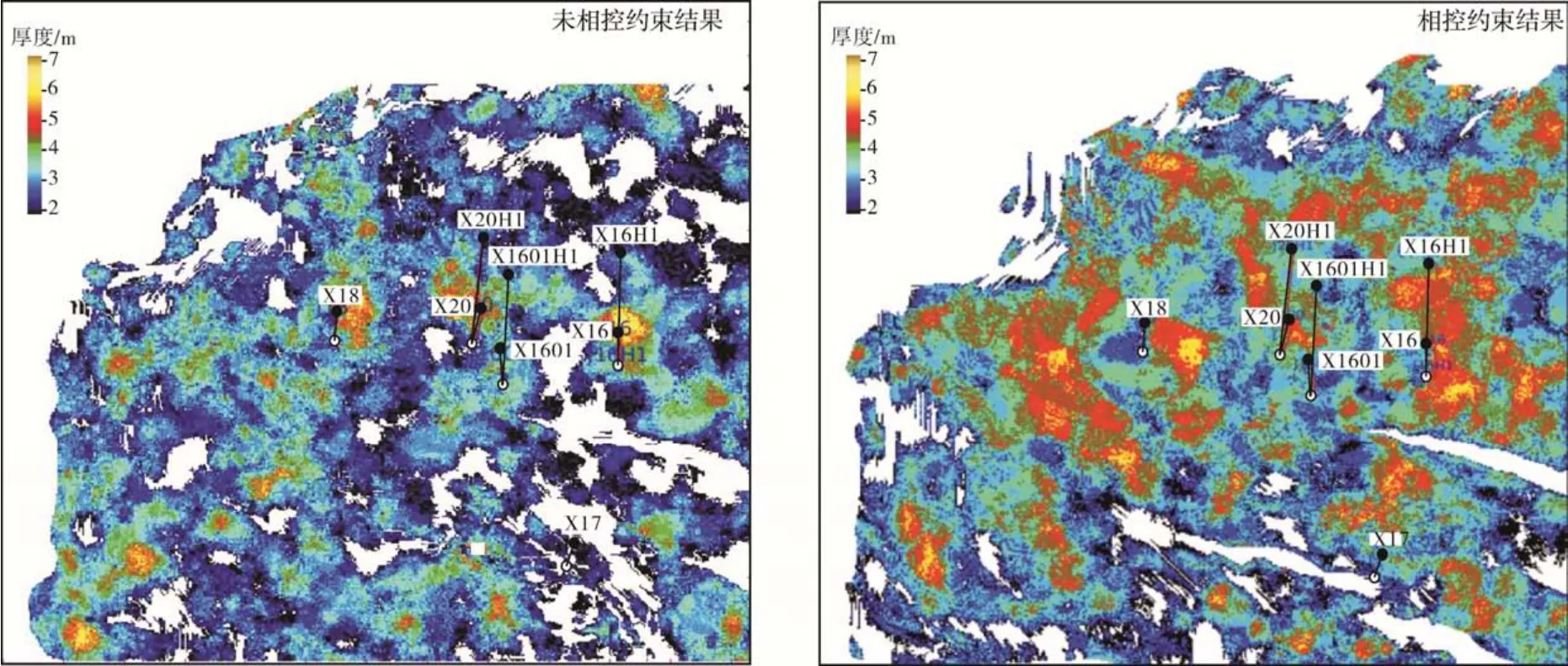
图9 相控约束前后阜三段上亚段砂体厚度分布

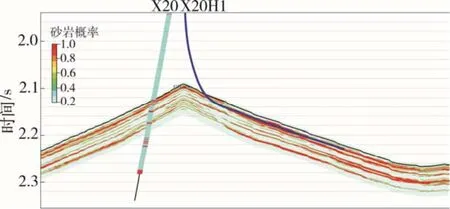
图10 储层预测结果过井剖面

4 结论

（1）利用基于主成分分析的地震相分析技术建立符合研究区滩坝沉积规律的地质模式，指导地质统计学反演参数的确定。

（2）将研究区沉积模式和地震相结果应用到基于马尔科夫链–蒙特卡罗算法的地质统计学反演进程中，实现了沉积相与随机反演的深度融合，有效降低了随机反演的不确定性，大幅度提高了储层预测精度。

（3）最终得到的砂体平面展布形态和地震相一致性好、符合研究区滩坝砂体沉积规律，垂向分辨率高，适用于储层垂向薄、横向相变快的复杂沉积环境下的储层预测。