基于Curvelet变换的线杆共振干扰去除方法
2022-04-28谢兴隆马雪梅龙慧明圆圆孙晟
谢兴隆,马雪梅,龙慧,明圆圆,孙晟
(中国地质调查局 水文地质环境地质调查中心,河北 保定 071051)
0 引言
野外采集的原始地震数据中往往含有各种类型的噪声,如何对地震资料进行噪声压制,突出和保护有效反射信号一直是地震处理中的研究重点。地震资料中的噪声也称为干扰波,成分复杂,一般分为不规则干扰和规则干扰,常见的噪声包括背景噪声、面波、声波、多次波等[1]。一般情况下,有效波和干扰波存在一定的频率、空间分布、振幅、视速度等方面的差异,根据差异性质,便可对不同干扰波选择有针对性的去噪方法,常见的去噪方法包含中值滤波、频域滤波、FK滤波、FX反褶积、KL变换、小波变换、多项式拟合等技术方法[2]。
小波变换是一种多尺度分析方法,具有较好的时频局部分析能力,在地震噪声压制领域应用较广[3-4],但小波变换角度分辨率不高[5],不能很好地表达图像边缘的方向特征。为了克服小波变换的局限性,Candès在其基础上提出了具有多尺度、多方向性特点的Curvelet变换。Candès等[6]于1999年提出了第一代Curvelet变换,其由Ridgelet变换发展而来,实现起来比较复杂,数据冗余量很大。其后,Candès等又逐渐提出了改进方法,也就是目前常用的第二代Curvelet变换,该变换是在连续域内进行定义,理论简单易用,有USFFT和 Wrapping 两种快速离散实现算法[7-9]。Curvelet变换的多尺度、多方向特性可以获得图像平滑区域和边缘部分的稀疏表达,在时变信号处理方面有着广阔的应用前景,基于Curvelet变换的地震资料处理也取得了一系列成绩,其中地震数据重建[10-13]、噪声压制[14-19]是研究的热点。在噪声压制方面,随机干扰[14-16]和面波噪声[17-19]是已有研究的主要方向。虽然基于Curvelet变换的去噪方法层出不穷,但所有方法研究的重点有两个,一是在Curvelet变换特点的基础上联合其他方法的优势形成多方法联合去噪技术,二是根据不同的指标或系数设计合适的阈值和阈值函数,从而提高去噪效果。
近些年,笔者在雄安新区使用可控震源进行中浅层地震勘探时发现线杆共振干扰严重影响了本区地震数据的质量,浅部数据的信噪比下降得尤为明显。线杆共振干扰是沿着线杆方向进行地震勘探时的一种规则性干扰噪声,此种干扰在借助已有道路进行地震作业时较为常见。由于石油、煤田地震勘探很少涉及此类干扰,线杆共振干扰没有引起充分重视,缺乏相关研究内容,而此类干扰却是中浅层地震勘探中常见干扰,因此对线杆共振干扰进行相关研究非常有必要。诸如FK滤波、中值滤波等常规去噪方法虽然对线杆共振干扰有一定的压制作用,但效果并不明显,有效波损失较多。本文借助Curvelet变换的多尺度、多方向特性,提出了一种基于Curvelet变换的线杆共振干扰去除方法,取得了较好效果。
1 线杆共振干扰的形成及特点
为了提高施工效率,降低施工成本,中浅层地震勘探经常需要借助已有道路进行测线铺设。而随着社会的进步与发展,道路(包括田间土路)两侧经常会有通讯、输电等线杆设施,典型的线杆如图1a所示,在存在线杆设施的道路进行地震作业时就容易产生相应的线杆共振干扰。
经过大量施工经验总结,我们对线杆共振干扰的形成有了较为清晰的认识,线杆共振干扰形成的示意如图1b所示。当可控震源车在某一线杆附近进行激发时,同时带动该线杆进行共振,共振信号通过线杆然后经由线杆顶部的线缆传至其他线杆,从而引发整个线路上线杆的共振,进而在线杆底部产生干扰的地震波。需要说明的是,当线杆之间的线缆间断或通过地下连接,共振干扰也会间断。影响线杆共振干扰能量的因素较多,其能量表达公式为:

图1 线杆照片(a)及线杆共振干扰形成示意(b)Fig.1 Photo of poles(a) and schematic diagram of the pole resonant interference(b)
A=α1α2α3A0,
(1)
式中:A为某一线杆共振干扰能量;A0为震源激发的原始能量;α1为震动信号经过地面时的能量衰减系数,主要受传输距离影响;α2为震动信号经过线杆的衰减系数,主要受线杆材质、埋深、大小等因素影响;α3为震动信号经过传输线缆的衰减系数,主要受传输线缆的材质、数量、粗细等因素影响。某一线杆共振干扰的综合衰减系数为α1、α2、α3,综合衰减系数主要反映了共振干扰对地震数据的影响程度。
同样,线杆共振干扰在地震记录中的初始时间,由下式决定:
t=t1+t2+t3,
(2)
式中:t为线杆共振干扰的初始时间;t1为地面传递时间;t2为线杆传递时间;t3为线缆传递时间。
为了模拟线杆共振干扰,我们设计了如图2a的简单正演模型。地下为两层地质结构,上地层的速度、密度分别为1 200 m/s、1.8 g/cm3;下地层的速度、密度分别为2 000 m/s、2.0 g/cm3;两层的分界面深度为200 m。正演中采用主频40 Hz的Ricker子波进行零偏激发,96道接收,道间距5 m,其中首道定义为0 m。线杆紧邻测线,分布在0、200、400 m三个位置,假设线杆产生共振后,即可当作独立震源,其中0 m线杆与震源位置一致,无法体现共振干扰。200、400 m处的线杆共振干扰的综合衰减系数分别假设为0.08、0.02,初始时间分别假设为60、240 ms。
最终正演结果如图2b所示,虽然综合衰减系数较小,但共振干扰的位置及影响清晰可辨,干扰能量主要来自线杆共振时激发的能量较强但衰减较快的面波成分。实际情况要比理论模型复杂得多,真实的野外记录如图3所示,线杆共振干扰波均匀的分布在地震记录上,以线杆为中心表现为明显的扫帚状低频干扰波,局部能量较强。图3a中的干扰较小,未对350 ms反射轴形成明显影响,图3b中的干扰较大,350 ms反射轴基本无法分辨。

图2 正演模型(a)及正演的单炮记录(b)Fig.2 The forward model(a) and its single shot record(b)

a—共振干扰较小;b—共振干扰较大a—low interference;b—high interference图3 线杆共振干扰在实际地震记录中的表现特点Fig.3 The performance characteristics of pole resonant interference in real seismic records
由于中浅层地震勘探或城市地震勘探需借助道路进行野外施工,而道路两侧的线杆又无法完全避免,因此,线杆共振干扰的问题直接影响着了中浅层地震勘探的数据质量。
2 方法原理
2.1 曲波变换原理
Curvelet变换原理及相关算法,已有较多文献进行了详细介绍,本文只进行简单说明。Curvelet变换与小波变换相比增加了方向信息,是小波变换的二维扩展,与其类似,也可以进行平移伸缩。Curvelet变换具有旋转特性,其系数由j、l、k1、k24个因子确定,其中j为伸缩因子,l为旋转因子,k1和k2为平移因子。常用的第二代Curvelet变换公式为:
(3)
式中:j表示尺度;l表示角度;k表示位置;函数f∈L2(R2)是目标函数;φj,l,k是Curvelet函数;C(j,l,k)是Curvelet系数由目标函数与φ内积得到。
曲波变换包含精细尺度和粗尺度的分量,但粗尺度的曲波没有方向性,因此整个曲波变换可以看成是由精细尺度下的各向异性元素和粗尺度下各向同性元素共同组成的集合。一般利用Curvelet变换进行信号处理时,会将信号进行尺度和方向的划分,明确待处理信息所在的尺度与角度,从而进行细致处理。
快速离散实现算法有Wrapping算法和USFFT 算法两种,当输出相同结果时,Wrapping 算法运算速度更快,效率更高,考虑到地震原始数据量较大,故文中选用 Wrapping 算法进行运算。
2.2 Curvelet域线杆共振干扰的去除及步骤
线杆共振干扰的特点前文已经介绍,根据干扰波与有效波在频率、速度、方向上的特征差异,将干扰波与有效波变换至Curvelet域,利用Curvelet变换的多尺度、多方向特性可以更细致地描述干扰波与有效波之间的差异,这也是相对于传统去噪方法存在的明显优势。
假设一个地震记录表达为y(c,t),其中c表示CDP号,t表示时间。设s(c,t)为有效信号,x(c,t)为线杆共振干扰信号,n(c,t)为其他噪声信号,则实际地震记录可以表示为:
y(c,t)=s(c,t)+x(c,t)+n(c,t) 。
(4)
对地震数据体进行Curvelet变换,则在Curvelet域中可表示为:
Cy(j,l,k)=Cs(j,l,k)+Cx(j,l,k)+Cn(j,l,k) ,
(5)
式中:Cy(j,l,k)、Cs(j,l,k)、Cx(j,l,k)、Cn(j,l,k)分别为y(c,t)、s(c,t)、x(c,t)、n(c,t)的Curvelet变换系数。在原始记录中,有效信号与线杆共振干扰叠加在一起,不好分离,通过Curvelet变换将地震数据扩展到Curvelet域的三维空间中,可以对不同信号进行最大程度的分离。
基于Curvelet变换的去噪方法大多是阈值法或是在其基础上的改进方法,利用有效波与干扰波在Curvelet域的差异,设计或选择合适的阈值函数,就能实现压制噪声的目的。常见的阈值函数包括硬阈值、软阈值、线性阈值与非线性阈值等类型的函数。经硬阈值处理的Curvelet系数阈值附近不连续,容易产生“伪Gibbs现象”;软阈值考虑到了系数的平稳变化,但与真实系数存在恒定的偏差。为了克服硬阈值与软阈值函数的缺陷,结合线杆共振干扰的特点,本文设计了一种非线性阈值函数,表达如下:
(6)

(7)
式中:A为待处理数据的集合;t1为待处理数据的中值;λ为控制参数。待处理数据集合A随尺度变化,因此阈值也是随尺度进行变化。
基于Curvelet变换的线杆共振干扰去除方法的具体步骤为:
1) 应用Curvelet变换将原始地震数据分解为多个尺度,首先确定受线杆共振干扰的尺度与不受线杆共振干扰的尺度。
2) 根据线杆共振干扰的分布规律,对受线杆共振干扰的各尺度进行方向分析,确定线杆共振干扰的方向。经过不同尺度、不同角度的优选从而将原始数据分为受线杆干扰的区域和不受线杆干扰的区域。
3) 线杆共振干扰与面波形态有些类似,但能量又弱于面波,为了更好地使用阈值函数,利用线杆共振干扰与有效信号之间的视速度差异,对干扰数据中含有较多有效信号的尺度进一步进行FK滤波分离。
4) 对分离出含有线杆共振干扰的数据在各个尺度选取不同阈值,采用阈值函数对干扰信号进行压制。
5) 将对含线杆共振干扰区域压制后的Curvelet 系数与不含线杆共振干扰的Curvelet 系数相加,顺便在Curvelet域使用固定阈值[20]对随机噪声压制,然后反变换重构信号得到去除线杆共振干扰后的地震剖面。
本文所设计的阈值函数与面波压制所使用的阈值函数类似,都是基于干扰波的能量大于有效波能量的基础上,因此分离出的干扰信号区域含有的有效信息比例越少,则阈值函数使用效果越佳。不同尺度的阈值需要根据能量进行确定,设置控制参数有利于人工监控调节。
3 实际资料分析
以雄安新区容城县沙河村附近的原始记录为例,图4a为原始单炮记录,采用美国M18-612型可控震源进行激发,总道数120,道间距5 m,采样间隔0.5 ms。从单炮记录中可以观察到明显的线杆共振干扰,图中红色箭头所示。使用Wrapping算法对单炮记录进行5个尺度的Curvelet变换,图4b显示了所有尺度及方向的Curvelet系数,纵向分布较少,主要集中在横向。为了更好地进行说明,截取单炮记录中的50~100道,100~700 ms的区域(图4的黑框内)进行演示。
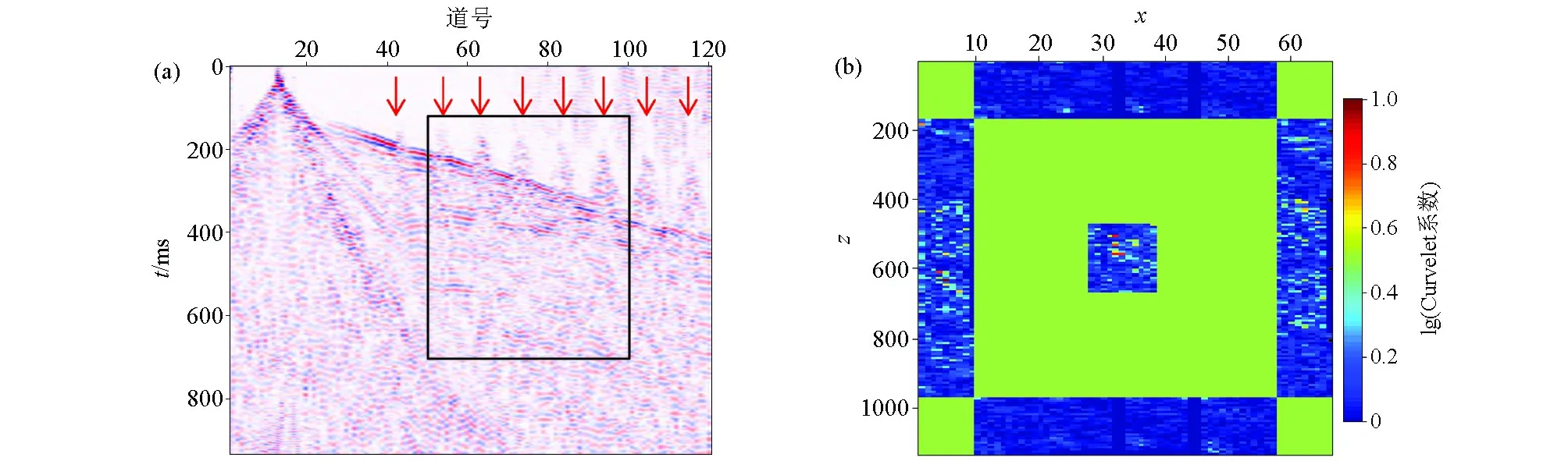
图4 原始数据(a)及其Curvelet系数分布(b)Fig.4 Original seismic record(a) and its Curvelet coefficient distribution map(b)
将原始数据进行Curvelet 正变换,得到5个尺度的Curvelet系数,分别对各尺度进行反变换,各尺度的地震记录如图5所示。从图中可以明显看出线杆共振干扰主要存在于第5尺度中,第1、2尺度几乎不含线杆共振干扰,第3、4尺度既包含干扰成分,又包含有效成分。
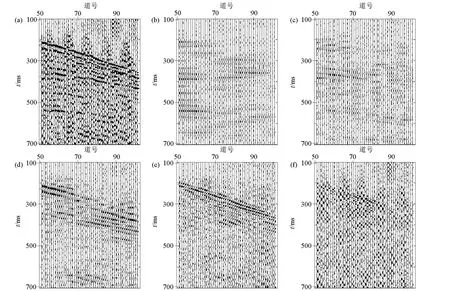
a—原始记录;b~f—分别对应1~5尺度的分解结果a— the original record;b~f—corresponds to the decomposition results on the scale of 1~5 respectively图5 原始记录及各尺度分解结果Fig.5 Original record and decomposition results at different scales
为了进一步缩小含有线杆共振干扰的数据范围,在各尺度的基础上进一步进行方向分析,利用Curvelet反变换进行分方向数据重构,详细观察含有线杆共振干扰的方向分量。由于第1、5尺度不存在方向性,第2尺度几乎不含线杆共振干扰,我们主要对第3、4尺度进行方向研究。以第4尺度为例,共含有32个方向分量,根据试验确定含有线杆共振干扰的方向分量分别为12、13、28、29。第4尺度含有线杆共振干扰的方向分量重构如图6所示,12、13分别与28、29方向分量相差180°,因此图6中a、b与c、d结果相近。
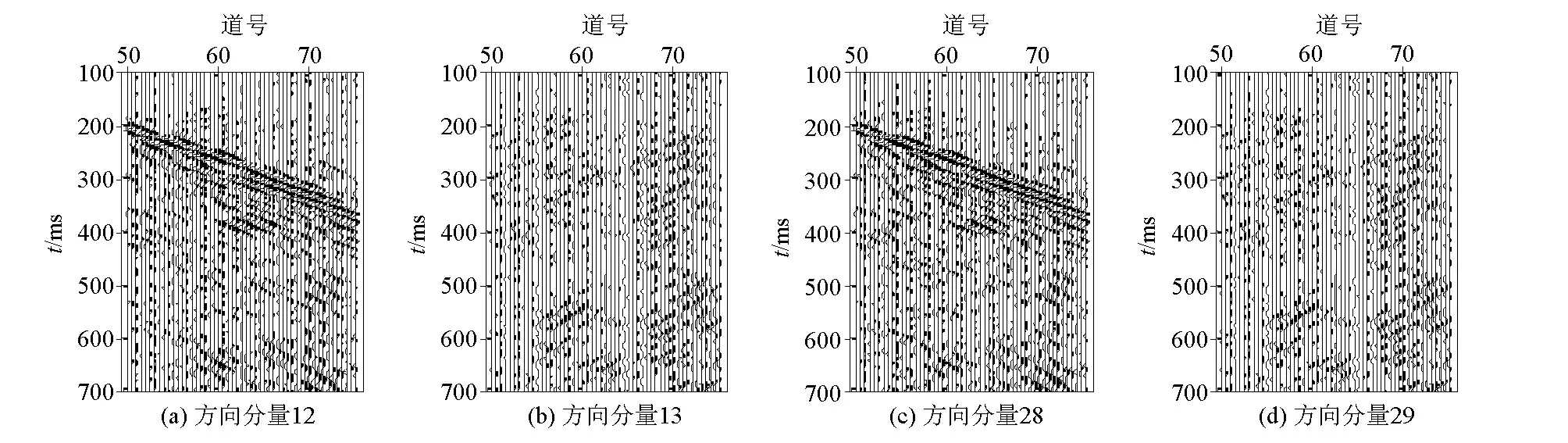
图6 第4尺度含干扰成分的方向分量Fig.6 Directional component with interference information at the fourth sacle
通过Curvelet域多尺度、多方向的分析明确了含有线杆共振干扰的数据区域,然后将含线杆共振干扰的Curvelet系数与不含干扰的Curvelet系数进
行反变换分别得到含线杆共振干扰和不含线杆共振干扰两种数据,分离结果如图7所示。图7a为同时含有有效信息和线杆共振干扰的数据,图7b为不受线杆共振干扰的数据,在图7b中已经可以较好地看到有关反射波的信息。

a—含线杆共振干扰数据;b—不含线杆共振干扰数据a—data with pole resonance interference;b—data without pole resonance interference图7 原始数据最终分离结果Fig.7 The final result of separating the original data
接下来按照第二节介绍的步骤,利用设计的阈值函数对含有线杆共振干扰的数据做进一步处理,最终去除的线杆共振干扰噪声如图8所示,去除的噪声表现出有规律分布的扫帚状低频记录。最终去除的结果如图9b所示,与图7b对比观察可以发现,经阈值函数处理后的剖面中有效信息更丰富,尤其是浅部200~350 ms的反射形态更为清晰。将原始数据与去噪结果进行对比(图9),可以看到,原始数据中的线杆共振干扰得到了有效压制,反射信号同相轴的连续性、清晰度均有所提高。频谱分析对比如图10所示,由于最后一步使用固定阈值压制随机噪声时添加了白噪声,因此去噪后的频谱在低频与高频段均出现了少量能量,能量占比较低,对有效频带宽度没有明显影响。经过频谱对比分析可得出,两者的有效频带宽度相近,但去噪数据在40~70 Hz优势频段的能量占比提高的较为明显,与实际记录对比结论一致,去噪数据的信噪比与分辨率均有提高。整体上,本文所提出的基于Curvelet变换的线杆共振干扰去除方法可以获得较好的去噪效果,能在最大程度保护有效信号的基础上分离线杆共振干扰波。
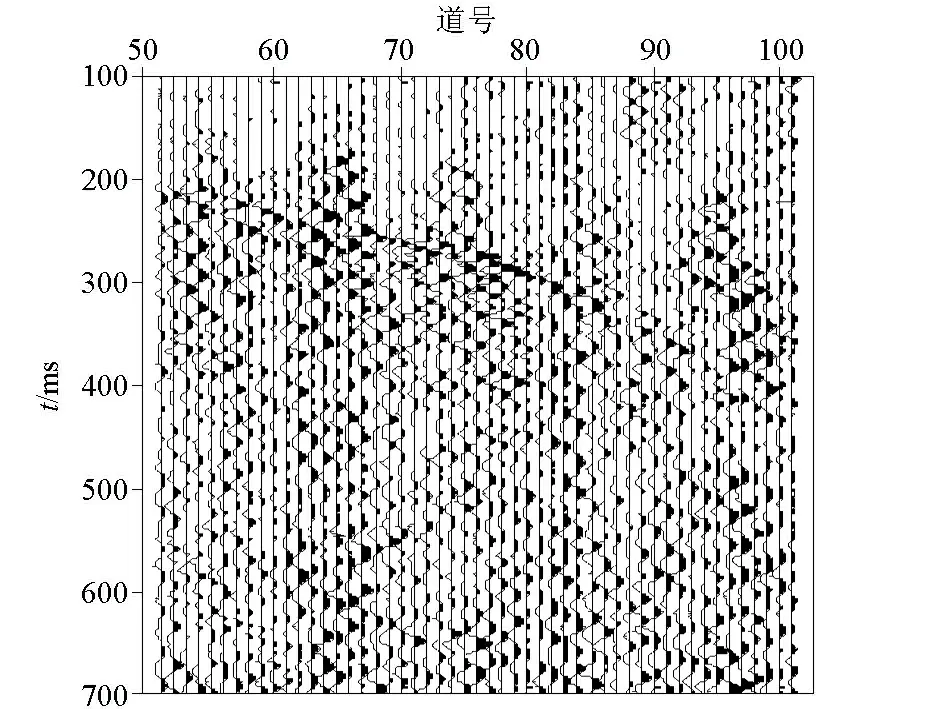
图8 最终去除的线杆共振干扰数据Fig.8 The final removal of the pole resonance interference data
4 结论
1)线杆共振干扰是中浅层地震勘探常见干扰之一,干扰大小主要和线杆规模、观测系统、震源能量有关,降低了地震原始数据的信噪比,尤其是对浅部数据影响较大。
2)Curvelet变换的多尺度多方向特征可以较好对含线杆共振干扰信号进行分离,能在彻底分离线杆共振干扰波的同时提取出更多的有效信号,对高保真地震资料处理具有重要意义。
3)本文设计的非线性阈值函数及去除线杆共振干扰的方法步骤效果明显,去噪后资料的信噪比及分辨率均有提高,达到了去除效果。
4)Curvelet变换在地震去噪中优势明显,根据不同噪声特点及处理目的,可以联合多种方法,设计合适的阈值函数,从而形成有针对性的去噪方法。
