降低数据稀疏性的多维时序序列时间戳对齐方法

李广盛，郑建立，车霞静

（1上海理工大学 健康科学与工程学院，上海 200093；2上海交通大学附属仁济医院，上海 200127）

0 引 言

在过去的二十年中，时间序列分类（time series classification，TSC）被认为是数据挖掘中最具挑战性的问题之一。随着时间数据可用性的增加，自2015年以来已有数百种TSC算法被提出。由于时间序列数据的自然时序性，几乎每一个需要某种人类认知过程的任务中都会出现时间序列数据。时间序列广泛存在各类研究工作中，包括电子健康记录、人类活动识别到声学场景分类和网络安全等领域。但由于种种原因，如收集错误、故意损坏、医疗事件、节省成本、设备异常等，往往会不可避免地出现丢失观测数据和不规则采样等现象，使得时序序列数据稀疏性大大增加，阻碍了分类任务的开展。

针对时序序列中缺失问题，从不同的解决方法来看，主要可以分为2类。一是以专家知识为基础进行手工填补和重采样；二是利用深度学习等方法实现端到端的数据填补及分类。前者主要利用专家知识，根据时序序列数据的观测变量等信息进行缺失值的填补和修正，后者利用深度学习强大的抽象表征能力和拟合能力来实现数据的填补和分类［11-14］。

基于专家知识的方法尽管可解释性较强，但是却费时费力；而基于深度学习方法在原始数据集上直接填补尽管能够取得不错的效果，但是却忽视了不规则采样等问题。此外，数据集中可能存在部分数据缺失率过高，使得模型无法抽取其潜在信息，模型的填补效果大打折扣。本文提出一种基于数据集中自带的时间戳数据，通过数据时间戳对齐和下采样方法，在多个公开数据集以及私有数据集和近年来提出的深度学习时序序列分类算法上的实验表明，该方法能够在基本不损失模型效果的同时，有效减小数据集的稀疏规模和模型训练时间。

1 相关方法

在本节中，本文先给出多维时序序列的相关定义，之后将相关方法分为时间戳对齐和基于分布密度的下采样两步讲述，具体流程示意图如图1所示。

图1 时间戳对齐和下采样流程示意图Fig.1 Schematic diagram of time stamp alignment and downsampling process

1.1 多维时序序列的定义

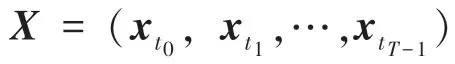
1.2 时间戳对齐

由于数据集的不规则采样，导致虽然数据采样点的时间跨度非常大，但是数据点的个数却非常少，具体到每一个样本更是不尽相同。例如在Physionet数据集中，总共有48×60 min，共2 880个数据可采样点。但事实上该数据集中最大样本的数据采样点个数只有249，而最小样本的数据采样点个数只有1。考虑到深度学习模型在训练时一般采用小批量（mini-batch）做法，因此需要在较短的样本尾部填充无意义的屏蔽值（mask value），使模型的输入等长。但是这样的对齐在RNN模型中是有缺陷的，RNN模型的每一个时刻输入是mini-batch在时间维上的切片，上述做法会使得切片中包含的不同样本数据点没有对齐，即样本的t时刻的数据和样本的t时刻数据同时输入RNN模型，这样会导致模型效果欠佳。因此，需要做数据对齐。

首先本文根据时间戳的最小粒度和其时间跨度，构建一个具有最长数据点长度的无值背景板，再根据原始数据对应的时间戳将每一个数据点嵌入其中，这样就得到了一个完整的所有样本数据点都对齐了的数据集，实现了数据点的物理位置和逻辑位置的统一。根据上述做法，Physionet数据集的维度从原始的3 994×203×41，最终则转换成了3 994×2 881×41。

1.3 基于数据分布密度的下采样

在将数据对齐后，数据集的稀疏性会进一步扩大，需要做进一步的处理来减小数据集的稀疏性。本文定义在时间轴上的数据集分布密度函数，具体如下：

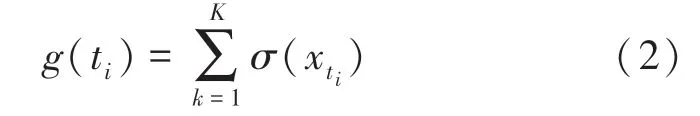
根据定义可知，当（）较小时，说明样本在对应时间戳∈［t，t）中分布较少，该区间的稀疏性较大。本文通过求解该区间所有观测变量的均值来替代该稀疏区域，实现数据稀疏性的减小，计算公式如下：

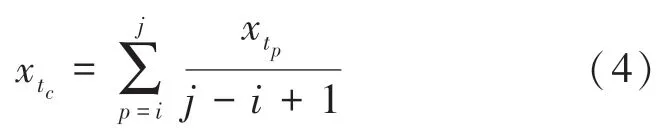
其中，t可用如下数学公式计算得出：

图2给出了Physionet数据集原始和预处理后的数据密度分布图像。从图2中可以明显看出，经过预处理的数据在时间轴上的分布密度显著提升，并且基本保留原始分布密度的分布趋势。

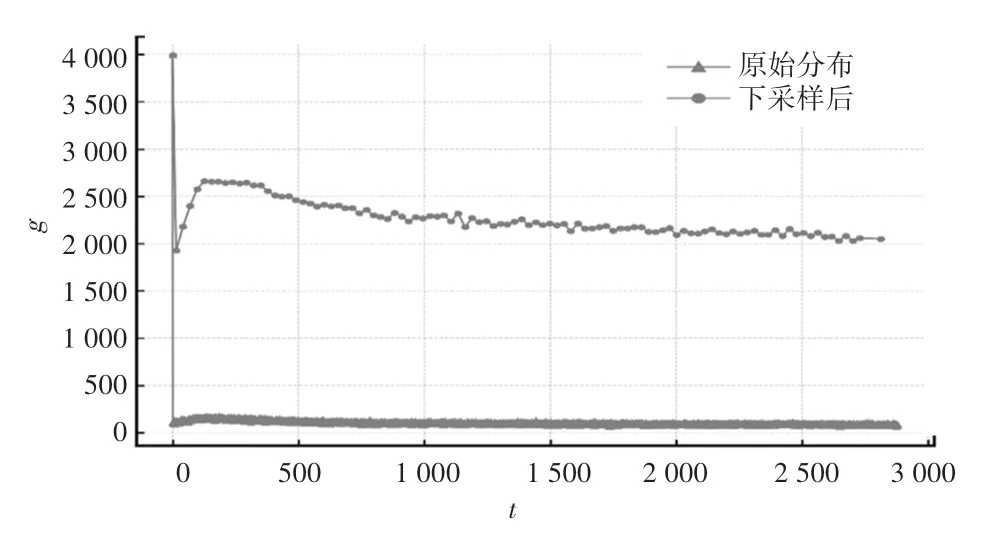
图2 Physionet数据集数据分布密度Fig.2 Data distribution density of Physionet data set

在经过预处理后，Physionet数据集大小从经过时间戳对齐后的3 994×2 881×41转换成了3 994×100×41。对比该数据集原始的大小可以发现，经过处理后的Physionet数据集的大小是原来的0.493倍，显著减少了数据集的尺寸。

2 实验结果

2.1 数据集

Physionet challenge 2012是physionet.org在2012年举办的一个多维时序序列分类和回归比赛。该比赛使用的数据是12 000名因心脏病、内科、外科等原因而住院的ICU病人的记录，包括白蛋白（Albumin）、碱性磷酸酶（ALP）、谷丙转氨酶（ALT）等36个观测变量和年龄、身高、体重等6个一般描述符，共42个变量。除一般描述符外，囿于病人身体状态差以及医疗设备工作性质等原因，在36个观测变量中有很多缺失值，且每一个观测的时间间隔也不相同。数据集中给出了每一个观测的相关时间戳，该时间戳的分度值是分钟，即时间的最小粒度为每分钟。该挑战赛设立了5个分类任务和一个回归任务。本文主要使用的是其中的死亡预测任务，即预测病人在48 h后是否死亡。这也是下文涉及的算法在提出时被使用到的任务。

MIMIC-III Clinical DataBase是一个大型的公开数据库，其中包括了2001年至2012年期间在美国BIDMC医疗中心重症监护病房住院的超过4万名患者的已确认的健康相关数据。该数据库包括人口统计信息、在床边进行的生命体征观测、实验室检测结果、程序、药物、护理记录、影像报告和死亡率等记录。通过数据挖掘、信息提取等手段，从该数据库中提取了份存在大量缺失值和不规则采样的ICU住院病人48 h内的时序序列数据、对应的时间戳和死亡预测标签。该数据一共有12个观测变量，包括血氧饱和度（SpO2）、心率（HR）、呼吸速率（RR）、收缩压（SBP）等。和Physionet一样，本文也是使用其作为分类任务。

肾移植术后数据集是来自某三甲医院肾移植科的931名肾移植患者术后生理检查的数据集，其中包括血常规、尿常规和血药浓度等共87个观测变量。该数据集的时间戳较为特殊，以肾移植手术当天为第零天，手术后所做检查的时间戳都为正整数，手术前所做检查的时间戳皆为负整数，时间戳的单位长度为一天。一般肾移植患者术后需住院几周，因此，数据在第零天周围分布比较密集。之后因病人经济原因、个人意愿以及地域等因素，使得病人做生理检查次数较少、检查范围不全，从而导致数据分布十分稀疏且不规则。该数据集的标签分为感染、排异和正常三个类型，分别描述了病人肾移植术后自身免疫力水平低、高、正常对移植肾的影响。

图3给出了上述3个数据集原始缺失率和经过下采样后的缺失率。从图3中可以发现，肾移植数据集缺失率较另外2个数据集缺失率更高，下采样效果不明显，但是对于Physionet数据集和MIMIC-III数据集，下采样均有效降低了数据集的缺失率。

图3 3个数据集下采样前后缺失率对比图Fig.3 Comparison of missing rates among three data sets with and without downsampling

2.2 相关分类算法

GRUD，全称GRU-deacy。文献［12］通过分析缺失值的类型给出了2个缺失模式，分别是：固定缺失值模式和衰减收敛缺失值模式。其中，固定缺失值模式指某个观测变量的缺失值和该观测变量最早的记录值相同；衰减收敛缺失值模式指观测变量在经过较长时间变化后逐渐收敛，如MIMIC-III中SpO2等观测变量。研究中根据这2种缺失值模式提出了填补函数，并将填补过程嵌入普通GRU模型，构建了一个端到端的对具有缺失值和不规则采样的多维时序序列进行分类的深度学习算法，在原始Physionet数据集实验表明，该算法能够有效地实现对病人死亡与否的预测，其达到了0.831，是一个强有力的基线。

Interp-net通过构建了一个插值网络来捕获输入数据的平滑趋势、瞬态和观测强度信息共三个维度的信息，以适应使用稀疏和不规则采样数据作为有监督学习输入的复杂性，从而得到一个规则间隔和无缺失值的输出，在此基础上将利用预测网络计算出最后的分类结果。与GRUD不同的是，该模型完全是模块化的，其插值网络和预测网络是分开的。在原始MIMIC-III数据集上达到了0.853。

2.3 结果

由于3个数据集标签分布并不均匀，因此本文采用ROC曲线下面积来衡量模型的效果。的计算方法同时考虑了分类器对于正例和负例的分类能力，在样本不平衡的情况下，依然能够对分类器做出合理的评价。实验中将数据集分为训练集、验证集、测试集，其比例为0.64：0.16：0.2。模型超参数均为模型研发者提供的默认值，其中，Physionet数据集和肾移植数据集的批次大小为128，MIMIC-III批次大小为256。

表1显示了上述模型在3个原始数据集和预处理后训练的最终效果。从表1中可以看出，模型在经过预处理的数据集上的效果几乎同模型在原始数据集上效果相同，损耗在0.003。

表1 GRUD、Interp-net模型在Physionet、MIMIC-III、肾移植数据集上AUC效果表Tab.1 AUC effect table of GRUD and Interp-net models on Physionet，MIMIC-III，and kidney transplantation data sets

本文还对比了上述模型在这2类数据集上训练所需时间，所有训练内容都在一张Nvidia Tesla P40显卡上进行。实验结果见表2，单位为hour／epoch。从表2中可以明显看出模型在经过预处理的数据集上达到收敛点的时间较短，能够有效地缩短模型的训练时间：在相同模型情况下，经过处理后的数据集的训练时间与原始数据集训练时间相比，平均减少了42.1%。尤需指出的是，肾移植数据集在GRUD算法上则减少了50%。

表2 GRUD、Interp-net模型在Physionet、MIMIC-III、肾移植数据集上训练时间表Tab.2 Training schedule of GRUD and Interp-net models on Physionet，MIMIC-III，and kidney transplantation datasetshour·epoch-1

3 结束语

本文提出了一种新的多维时序序列预处理方法。首先利用数据集自带的时间戳，实现原始数据在时间刻度上的对齐；然后通过观察数据集在时间轴上的分布密度来缩小分布密度较低的区间，最终得到一个规则采样且数据稀疏性大大减少的新数据集。实验结果显示与原始数据集相比，在基本不损失模型效果的情况下，该方法显著减小了模型训练所需要的时间。但是，该方法不够自动化，仍需要手动选择需要缩小的区间。因此，性能上更为优越的自动化是未来探索的方向。