基于两阶段分层组合优化算法的电力系统机组组合

何 旺，余登武

（1贵州大学 电气工程学院，贵阳 550025；2国网重庆市电力公司 万州供电公司，重庆 404100）

0 引 言

机组组合问题是指在满足系统安全约束和电能质量要求的前提下，利用合理的机制控制机组的开／关状态，调整各时段的出力，使某一调度周期（通常指一天）内的总运行成本最小化。机组组合是解决电力系统最优潮流和经济调度的前提。

机组组合问题是NP-hard型问题，具有高维、非凸、离散、非线性等特点，到目前为止，还没有好的解决办法。目前，机组组合的求解算法主要是2类。一类是传统算法，包括优化级表法、混合整数规划、动态规划法、拉格朗日算法等。文献［5］根据能耗指标形成了机组优先级排序表，并将优先级排序与内点法相结合，来解决机组组合优化问题。在文献［6］中，提出了一种动态规划算法来解决包含电动汽车的单元组合模型的维数灾难问题。在文献［7］中，大规模0-1机组组合态用量子叠加态表示，并通过近似动态规划实现了大规模机组组合态空间的全局搜索。在文献［8］中，针对热电联产的经济调度问题，考虑机组爬升、启动和停止的约束条件，建立了电加热一体化系统优化调度的混合整数规划模型。为了解决电力现货交易背景下的机组组合问题，文献［9］利用拉格朗日乘子λ的模糊逻辑设置，建立了基于拉格朗日算法的机组组合调度模型，考虑了旋转备用、启动成本和最小停机时间等约束。另一类是基于智能优化的算法，包括遗传算法、禁忌算法、粒子群算法、模拟退火算法等。文献［10］提出了一种基于改进人工鱼群算法的大规模多目标单元组合优化模型，以解决问题规模扩大导致的计算时间长的问题。为了平衡机组组合问题的经济性和可靠性，考虑系统运行成本和稳定运行能力，文献［11］针对机组组合这一高维、非线性混合整数规划问题，提出一种结合修补策略的整数编码粒子群算法。文献［6］研究了包含电动汽车的机组组合模型，并将电动汽车的充电量和充电时间要求作为约束条件。针对传统正向动态规划方法求解大型机组组合问题时存在的“维数灾难”问题，设置禁忌表，防止重复路径搜索，减少计算量。虽然目前的研究方法已经取得了一些进展，但计算速度和精度仍然不尽如人意。大型电力系统机组组合的难点在于各时段机组可能运行状态的组合较多。以20台机组为例，一个时段可能运行状态的组合数为2＾20-1≈10＾6，而24个时段可能的运行状态组合数为（10＾6）＾24＝10＾144种，而每一种状态都需要计算一次最优机组出力，计算非常复杂。

针对大型电力系统，传统算法计算速度慢、无法求解的问题，本文提出了一种两阶段双层组合优化算法。首先，通过转移因子算法得到电力网络的功率转移因子矩阵，由此求得线路的输电容量约束。然后在给定机组近似出力情况下，以煤耗成本和启停成本最小为目标，通过遗传算法确定机组的运行状态。最后根据最优运行状态，运用非线性规划模型确定机组的最优出力。算例结果表明，本文提出模型能降低算法复杂度，解决了传统算法计算速度慢、无法求解的问题。

1 机组组合优化模型

1.1 目标函数

机组组合的优化目标的目标函数由运行、开机、停机三类成本构成，具体见式（1）：

其中，表示机组编号；为调度周期时间；F为机组的运行成本（元h）；F表示机组第个调度周期的出力（MW）；I表示机组第个调度周期的机组开停二元变量：1表示开机，0表示停机；SU表示机组在第个调度周期的开机成本，是一个关于时间的函数，有S U＝C×I×（1-I），C为一个常数；SD表示机组第个调度周期的关机成本，有SD＝C×I（1-I），C为一个常数。

1.2 约束条件

负荷平衡约束见式（2）：

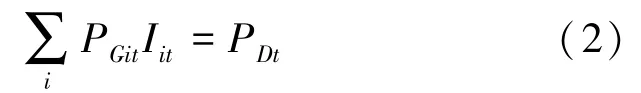
其中，P表示第个调度周期的总负荷。

上下限约束可写为如下公式：

负荷备用约束如式（4）所示：

线路安全容量约束见式（5）：

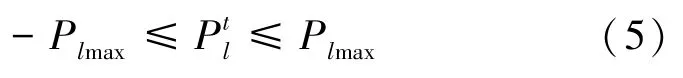
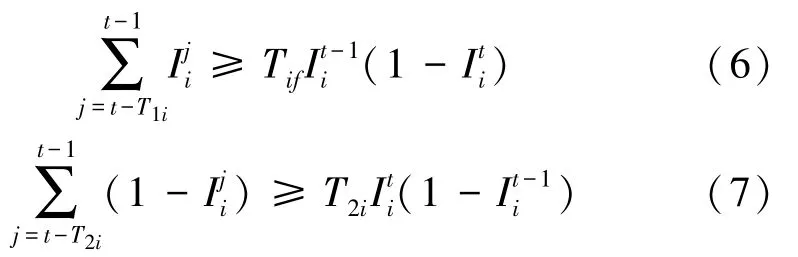
2 模型约束条件处理

模型中有许多约束条件，这些约束条件不能用程序直接表达，只能用变换来表达。

2.1 功率转移分布因子求解潮流约束

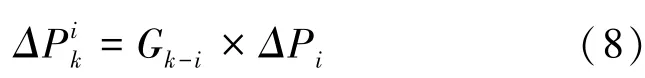
其中，G为第条支路第个节点的发电机功率转移分布因子。该值可由如下公式计算求出：

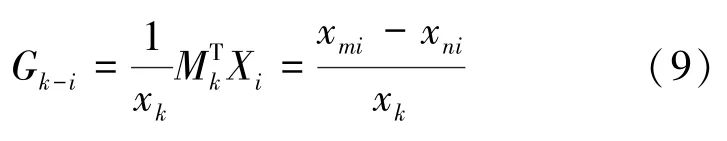
其中，x表示节点与节点之间的互阻抗，x表示节点与节点之间的互阻抗。

G描述了发电机的有功功率改变单位值时，支路的有功变化量。当节点流入单位功率时，支路上的电流是G。

2.2 开停机时间约束处理

机组启停时间约束难以处理，下面通过计算实例说明如何处理启停时间约束。

机组最小启动时间为3 h，最小停机时间为2 h，总调度周期为6 h。如果机组在开始时已启动1 h，则最小启动时间约束可写为如下计算公式：

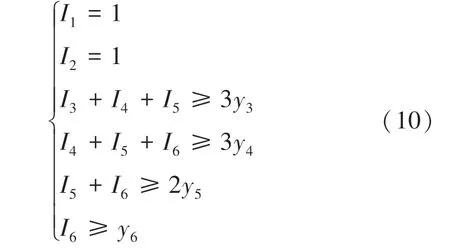
其中，I表示机组时段的开停状态，I＝1表示开，I＝0表示关；y表示机组时段是否发生开机行为，如果I＝0，I＝1，则y＝1，发生开机行为。

进一步地，研究推得的最小停机时间约束可表示为：

其中，I表示机组时段的开停状态，I＝1表示开，I＝0表示关；Z表示机组时段是否发生关机行为，如果I＝1，I＝0，则Z＝1，发生关机行为。

通过在程序中引入控制变量y，Z能有效表示出最小开停机时间约束。

3 两阶段双层组合优化模型

机组组合是一个NP-hard问题，首先要求解最优机组开停状态，每个机组开停状态对应有一个最优出力，求解最优出力时，模型包含了众多约束条件（每个时间有负荷平衡约束、上下限约束等条件，每个时刻每条线路有输电线路安全容量约束）。机组组合问题算法复杂度为指数级（P），属于在有限时间不可解决的问题。针对此类问题，有3个求解策略，分述如下：

（1）对于小型问题，可以直接解决。

（2）对于大型问题，采用近似算法来降低算法复杂度并获得精确解，但不容易获得最优解。

（3）对于大规模问题，可以提高计算机性能，如采用“量子计算机”；或利用互联网上的计算机的中央处理器的闲置处理能力，采用分布式计算。

方法（3）是提高计算机计算能力，但问题本身的难度并没有降低。本文针对方法（2）提出了一个两阶段两层组合优化模型。

3.1 非线性规划

非线性规划函数的流程如图1所示。该功能是输入给定的机组状态组合，并输出所有调度周期内所有机组的最优机组出力。具体步骤如下：

图1 非线性规划函数部分流程图Fig.1 Flow chart of nonlinear programming function

（1）定义1函数来求解单时刻的最优机组出力。传入参数为：当前时刻的总负荷、当前时刻各个节点的负荷矩阵、当前时刻各个机组的开停状态、当前时刻各个机组的出力上下限。输出为：当前时刻各个机组的出力、1的约束惩罚项。目标函数为：当前时刻的煤耗成本最小。约束条件为：负荷平衡约束、机组功率上下限约束、线路容量约束。

（2）输入6个机组所有时间的机组开停状态。

（3）判断机组当前时刻是否处于开机状态，如果处于开机状态，则机组功率要考虑斜坡约束和上下限约束；否则机组功率仅考虑上下限约束。图1中，表示机组第个调度周期的功率上限，表示机组第个调度周期的功率下限，［］表示机组的斜坡约束数值，表示机组第个调度周期的开停状态，［］表示机组的功率上限，［］表示机组的功率下限。

（4）将当前时刻的总负荷、节点负荷、各个机组的开停机状态、机组功率约束传入1函数。得到机组的出力、惩罚项。

（5）判断是否遍历完所有时间。如果遍历完，输出各个机组所有时刻的出力。

这里，1函数主要求解单一时间的机组出力（局部寻优），流程图完成全局寻优。

3.2 组合优化方法一

组合方法一流程见图2，把非线性规划函数嵌入进了遗传算法函数里。步骤如下：

图2 组合方法一流程图Fig.2 Flow chart of combination method 1

（1）定义遗传算法部分的目标函数和惩罚项：目标函数＝煤耗成本+启停成本；惩罚项＝机组最小开停机时间。

（2）初始化群体和参数（这里的群体指机组开停机状态数组），并要求群体满足负荷备用约束。

（3）得到开停机状态后，传入非线性函数规划部分求解得到各个机组的出力、非线性规划部分惩罚项。

（4）计算父代的适应度、惩罚项。惩罚项＝遗传算法部分的惩罚项+非线性规划部分的惩罚项。

（5）遗传选择、交叉、变异操作。

（6）将子代传入非线性规划函数部分，得到子代机组出力后，计算子代的适应度、惩罚项。

（7）子代与父代之间进行群体更新：优先选择惩罚项更小的个体，其次才是适应度更小的个体。

（8）判断是否迭代结束（达到一定迭代次数），如果迭代结束输出最优个体（开停状态和出力）、目标函数值。如果迭代没结束，跳到步骤（3）。

假设求解一个机组状态的算法复杂度为（1），求解一个机组状态对应的最优机组出力算法复杂度也为（1）。原始解法（同时寻优最优机组状态和最优机组出力）的算法复杂度即为（）。从图2中可以看出，组合方法一的算法复杂度为3（）。组合方法一在理论上可以寻优到最优解，具体看约束条件个数和规模数。

3.3 组合优化方法二

组合优化方法二流程见图3。步骤如下：

图3 组合方法二流程图Fig.3 Flow chart of combination method 2

（1）定义目标函数和惩罚项：目标函数＝启停成本+近似煤耗成本；惩罚项＝最小开停机时间。设每个机组每个时刻，近似出力＝（最大值+最小值）*开停状态。根据这个近似出力算出近似煤耗成本。

（2）初始化群体和参数（群体指机组开停机状态数组），并要求满足负荷备用约束。

（3）计算父代的适应度、惩罚项。

（4）遗传算法选择、交叉、变异。

（5）计算子代的适应度、惩罚项。

（6）子代与父代之间进行群体更新：优先选择惩罚项更小的个体，其次才是适应度更小的个体。

（7）判断迭代是否达到一定次数，如果是，输出最优个体（机组的开停状态），否则跳到步骤（3）。

（8）将机组开停状态传入到非线性规划部分，得到机组出力。

原始解法（同时寻优最优机组状态和最优机组出力）的算法复杂度为（）。从图3中可以看出，组合方法二的算法复杂度为（）（1）。组合方法二理论上很难寻优到最优解，但可以得到一个较为优秀的解。

4 算例

4.1 数据

以某地电网为例对本文模型进行有效性验证。该地是一个6机31节点系统。限于篇幅，机组参数、网络参数和各个节点预测负荷将不再赘述。机组开始时都处于开机2 h状态。网络结构具体见图4。

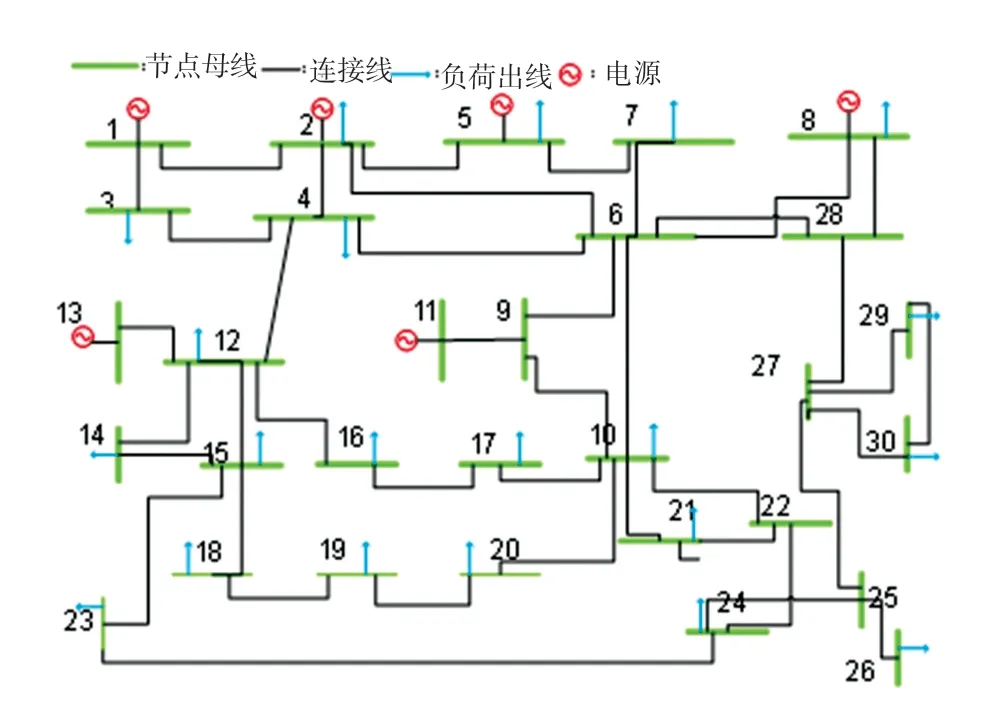
图4 网络结构图Fig.4 Network structure diagram

4.2 结果分析与对比

组合方法一和组合方法二的机组开停状态结果见图5，图6。机组出力见图7，图8。从上述图中可以看出机组1和机组2的优先级最高，基本处于开启状态，出力通常位于功率上限附近。

图5 组合方法一机组开停组合Fig.5 Unit on／off combination using combination method 1

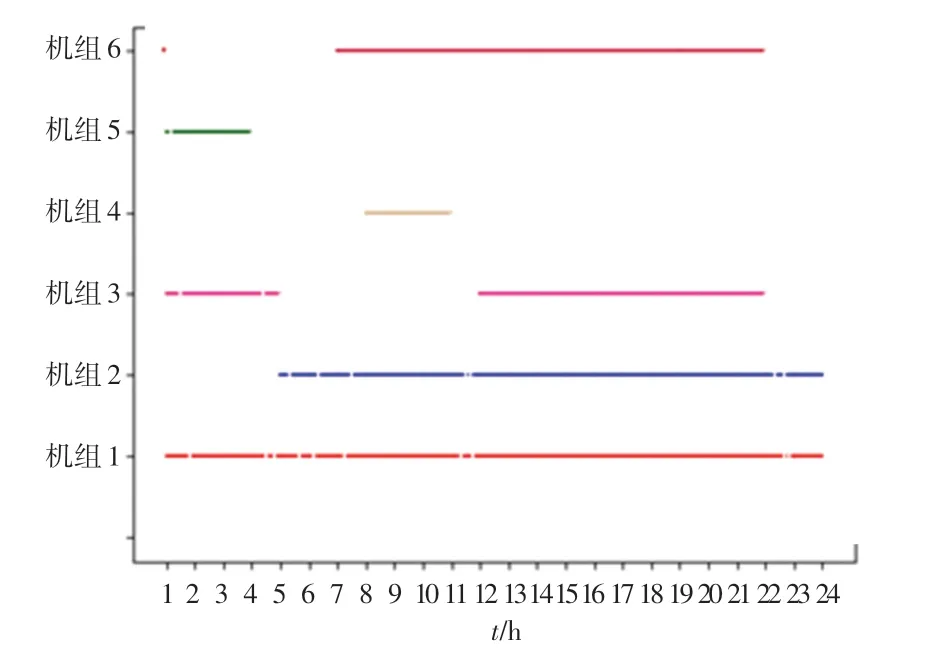
图6 组合方法二机组开停组合Fig.6 Unit on／off combination using combination method 2

图7 组合方法一求解机组出力结果Fig.7 Output result of the unit solved by combination method 1

图8 组合方法二求解机组出力结果Fig.8 Output result of the unit solved by combination method 2

各种方法的求解结果见表1，机组组合是一个NP-hard问题，在不使用分布式计算或计算机性能低下前提下，常规方法在有限时间内无法求解。组合方法一相比于常规方法，算法复杂度有所下降，求解速度仍然比较慢。组合方法二相比于组合方法一大大提高了运算速度，且求解结果靠近组合方法一。

表1 求解结果对比表Tab.1 Comparison table of solution results

5 结束语

本文提出了一种两阶段分层组合优化算法，以降低求解大型电力系统机组组合难题的算法复杂度，以非线性规划和遗传算法为两阶段优化算法，建立了机组组合的求解模型。在现实生活中，对于单元组合的NP-hard问题，一种是利用分布式计算来提高计算速度，另一种是利用组合优化来降低问题的复杂度，从而得到精确解。本文中的机组仅有火电机组，而网络约束只考虑功率容量，仅考虑了供电可靠性问题。未考虑供电优质问题（频率、节点电压、波形的约束）。后续，将考虑含有新能源机组和考虑节点电压的机组组合。