Turbo码中基4并行QPP交织器算法研究

史宜巧，李 丛

（1江苏电子信息职业学院 智能制造学院，江苏 淮安 223003；2南京理工大学 泰州科技学院，江苏 泰州 225300）

0 引 言

信道编码是提高信道可靠性的重要理论和方法，Turbo编码就是其中之一。Turbo编码应用了随机编译码条件，将卷积编码与随机交织器结合在一起，采用软输出迭代译码来逼近最大似然译码，从而获得了接近Shannon理论极限的译码性能。

Turbo由分量码和交织器级联而成，因此，分量码和交织器设计的优劣直接影响着Turbo码性能。其中，交织器主要功能是减小相邻比特之间的相关性，针对其研究主要从交织算法以及交织结构两个角度进行。文献［6］提出一种利用内存映射矩阵进行地址交织的方法，将每一个译码器的输出填充到标记为（）的存储器中，而这其中的映射关系由映射矩阵决定，但是矩阵需要使用退火算法逐级填充，求解过程较为复杂；文献［7］基于通用处理器（GPP）架构的实时信号处理技术，利用单指令多数据（SIMD）技术一条指令可以处理多个数据的特点，从指令级进行优化，提出一种高度并行的交织器，为DSP信号处理提供了良好的借鉴。为了消除并行交织译码过程中可能带来的地址冲突，引入了二次置换多项式交织算法（QPP），该交织器具有2个特点，一是从个并行SISO计算出来的个外信息在解交织后，总能够被存入到个不同的存储器中；二是该交织器是个并行SISO所需要访问的个交织地址总是指向个存储器的同一个位置。文献［9］提出一种基于置换模式的优化交织器方案，该方案利用一个统一的交织硬件电路来计算所有并行的交织地址。其交织电路的设计虽然较优，但由于需要保存不同配置下的初始交织模式，因而总体的硬件复杂度较高。文献［10］针对实际译码过程中，为了满足高阶蝶形运算需求，设计了一种基4蝶形交织器模型，通过奇偶地址分模块并行计算实现，然而该模型中相邻地址计算存在依赖，地址计算过程中递推关系复杂。

为了更好地发挥交织器在Turbo译码中的作用，简化硬件实现，本文提出一种基4并行QPP交织器算法。文章内容安排如下：首先介绍QPP交织器原理，并通过递推简化交织地址在并行计算情况下存在的求余等复杂运算；然后进一步推导公式解除相邻交织地址计算的依赖关系，从而提出本文的QPP基4交织器；最后对本文提出的算法使用Verilog语言设计实现，并借助FPGA仿真工具与Matlab仿真结果对比，结果表明本文算法用于FPGA实现交织输出结果完全正确，并且通过相同工艺下的与其他方案对比，显示本文设计综合面积减小50%左右，证明硬件开销更小。

1 QPP交织器原理

3GPP在LTE标准中采用了二次置换多项式（QPP）交织器作为Turbo码的内交织器，通过二次多项式推导计算交织地址，最终转换为递推计算。

1.1 QPP交织器递推运算

QPP交织器中，输出的下标和输入下标∏（）的关系满足如下二次方程式：

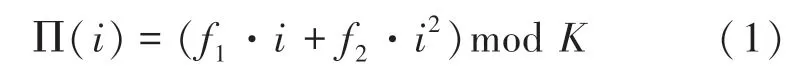
其中，和取决于块的大小，在文献［11］中，3GPP一共规定了188种不同长度的。

文献［12］对∏（）求解做进一步推导，如下：

其中，（1）（2（1））mod，很容易得知∏（）可以根据∏（1）和（1）递推获得。

1.2 并行QPP交织器设计

考虑到高速Turbo码并行译码设计的需要，交织器也需要并行设计，可以将均分为个子块，一般{1，2，3，4}，以4为例，则每个子块长度4，分块后交织过程如图1所示。

图1 交织器并行计算示例Fig.1 Example of interleaver parallel computation

由文献［13］可知，QPP交织器是一个无竞争交织器，即：

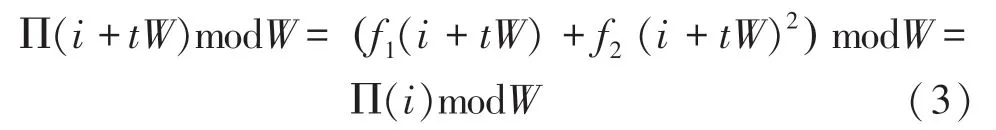
其中，＝｛0，1，2，3｝，表示块编号。先假设0，由于交织分块进行，可以重新表示为：

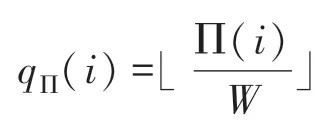
由式（3）可知，第时刻并行输出的4个交织地址块内偏移量∏（）是一致的，因此每次并行计算出4个交织地址，实际上只需要计算出一个偏移量（）。

首先是∏（），由于4·，那么可得（mod）modmod，已知求余运算有以下性质：

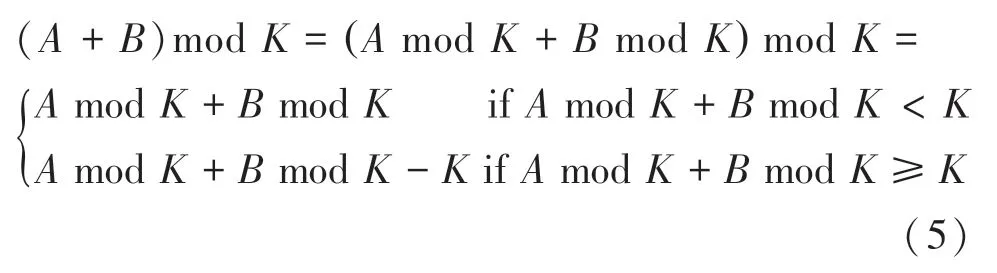
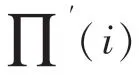
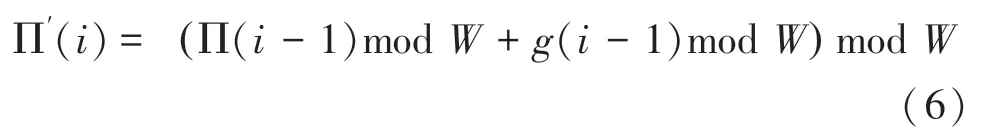
为简化运算，使硬件实现中不出现求余运算，令g（）（）mod，代入式（6），再结合式（5）性质可得：

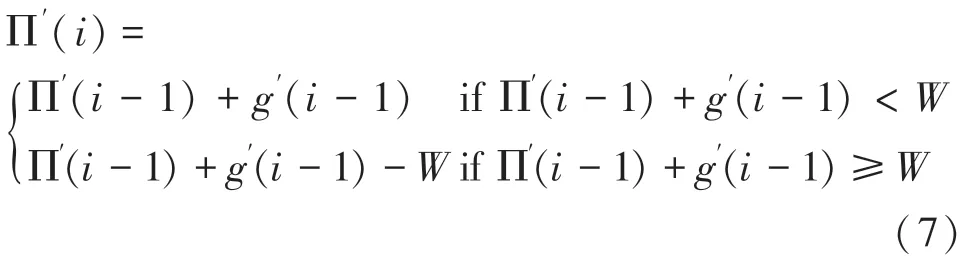
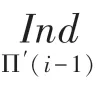
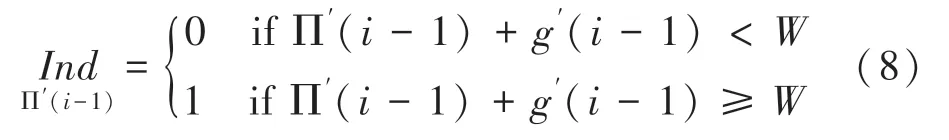
从式（9）可知，∏（）可以根据∏（-1）和g（-1）递推得到。将g（）＝（）mod代入式（9）可得：

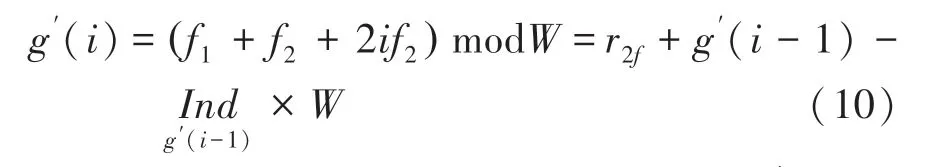
其中，＝（2）mod。由上式可知，g（）可以通过g（-1）递推得到。参照∏（）推导过程，同样有：

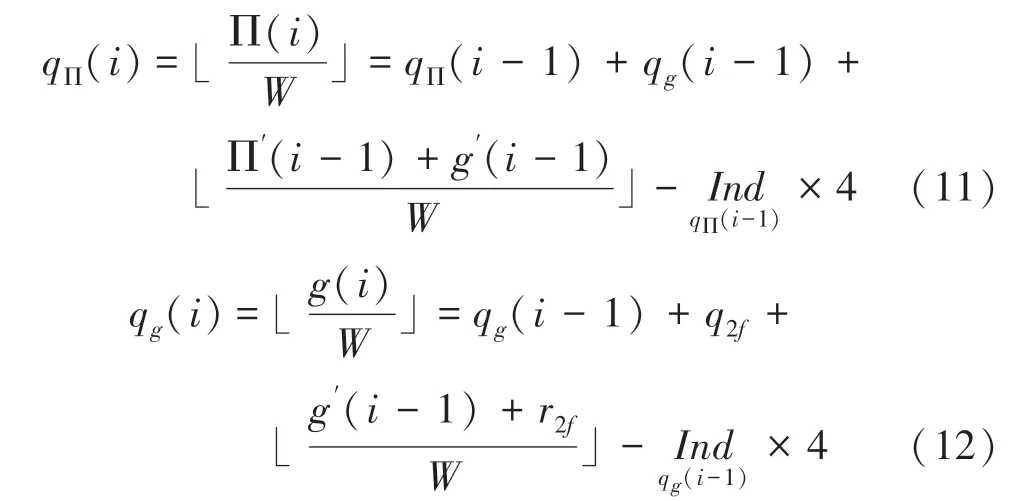
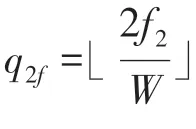
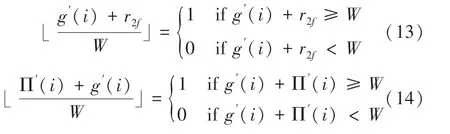
上述求解仅仅是针对（），而（）（｛1，2，3｝）可以根据（）求解，推导公式如下：

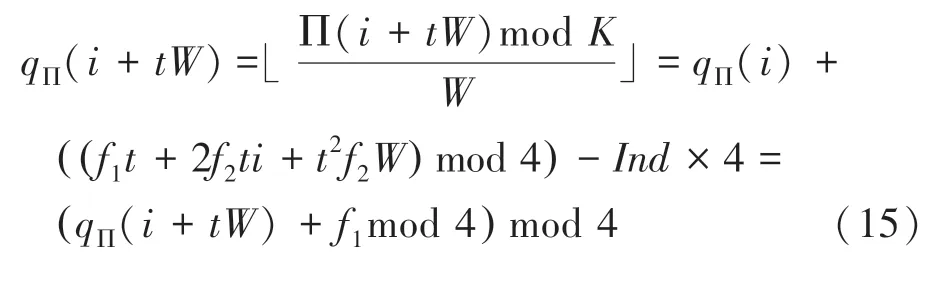
2 基4并行QPP交织器算法设计

每时刻每个子块仅输出一个地址，因此递推关系也仅存在于相邻2个地址间，而实际的Turbo译码系统需要面临高阶蝶形运算需求，例如基4蝶形译码系统中需要交织器同时输出奇偶地址，如图2所示。因此本文考虑设计一种算法，通过初始地址一次性计算得到奇偶地址。

图2 基4并行QPP交织器结构示意图Fig.2 Schematic diagram of radix-4 parallel QPP interleaver

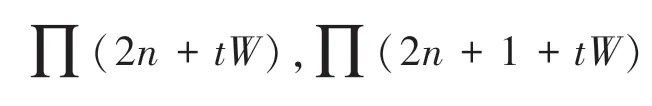
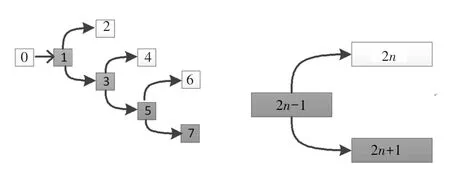
图3 交织器算法原理图Fig.3 Schematic diagram of interleaver algorithm

由图3可知，要同时计算出2与2+1两处地址，需要推导两者与2-1处地址的关系。根据上述分析，计算交织地址采用递推的方式，2与2+1处的地址实际上是相邻的，因此存在递推关系，以g（）为例，根据式（10）有：

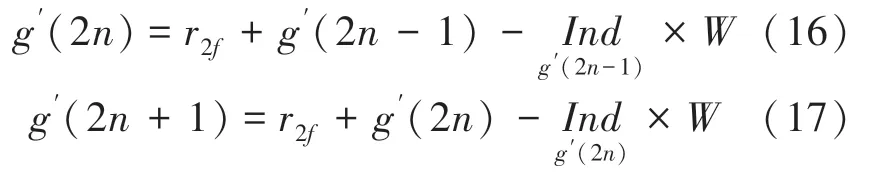
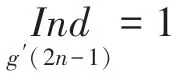
从式（16）和式（17）中可以看出，g（21）的计算依赖于g（2），这样奇偶地址无法同时计算。为消除两者之间的依赖关系，对式（15）作进一步递推，将式（16）代入式（17）可得：

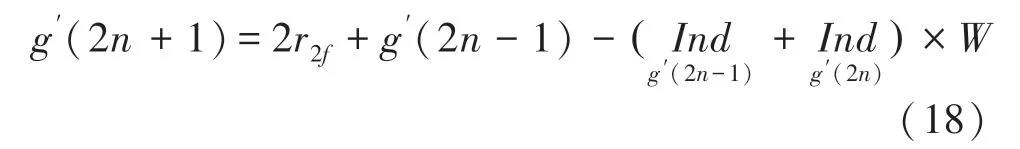
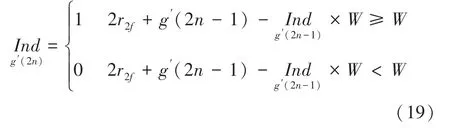
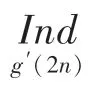
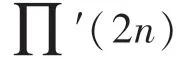
算法：计算Π（2）与Π（2+1）

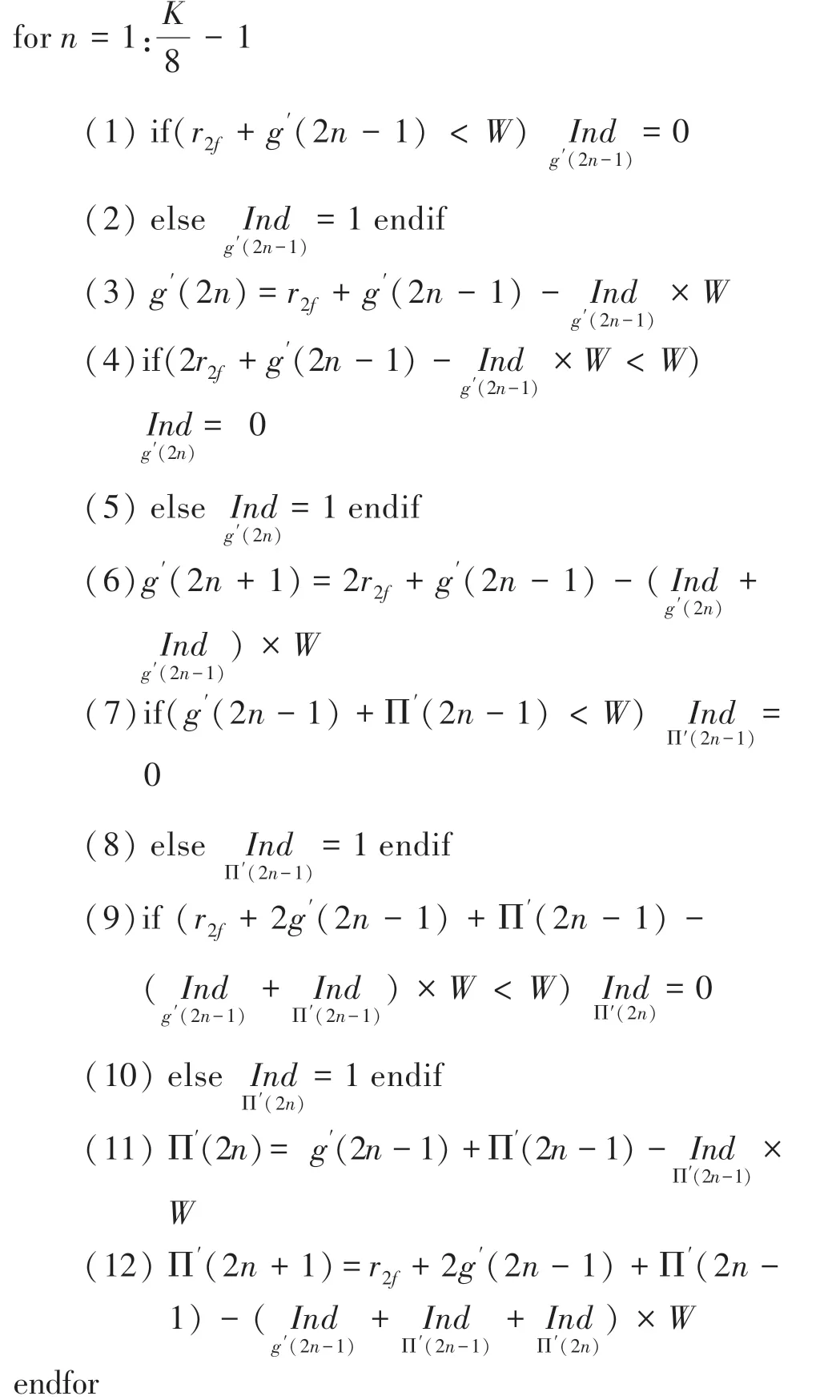
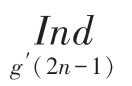
q（2）与q（21）以及（2）与（2+1）的计算类似，即通过往后递推一步，解除时刻计算2与2+1两处地址所需变量之间的依赖关系，保证奇偶地址可以同时输出。

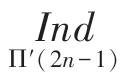
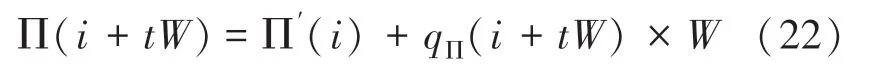
可以看出通过本文设计，能够实现利用单个输入计算输出多个地址，即单输入多输出（SIMO）。

3 FPGA设计与仿真分析

为了证明本文设计可行性，对以上提出的算法使用FPGA实现，验证仿真结果，并与已有方案进行对比，实现语言采用Verilog。

3.1 FPGA设计与硬件复杂度

交织器的顶层电路如图4所示，主要包括查找表模块与交织模块两部分，其中后者主要为前者计算交织地址提供输入。这是因为交织地址的计算是递推过程，需要提供初始值与必要的参数。

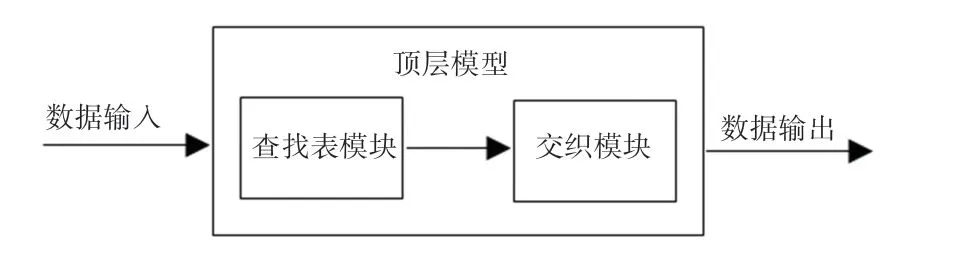
图4 顶层模块图Fig.4 Top module diagram

其中，交织模块的内部实现如图5所示，可以看到整个模块都被简化成了判决单元与一些计算单元，而根据第2节代码可以知道这些计算单元只包括加减运算，因此综合出来的电路非常简单。另外可以看出上一轮计算得到的g（）、∏（）以 及q（）都要作为返回值参与下一轮计算。

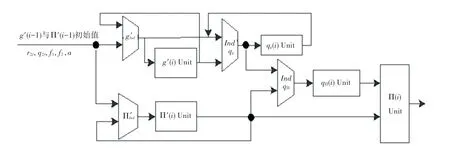
图5 交织模块实现Fig.5 Interleaver module

将所设计的交织器的硬件复杂度与已有的技术方案进行对比，在SMIC40 nm工艺下对本文设计进行综合，并与文献［9］和文献［16］所提出的方案进行了对比，见表1。表1中，文献［9］采用radix-4，每个时钟通过8个SISO并行的方式输出8个地址。文献［16］采用radix-2，最高4个SISO同时运行，也就是每个时钟输出4个地址，并且硬件实现包含了除法器。而本文的设计通过4个SIMO并行运行每个时钟输出8个地址。本文设计的综合面积仅有0.032 nm，通过归一化面积比可以看出，本文方案相对于另外2种方案硬件开销很小。

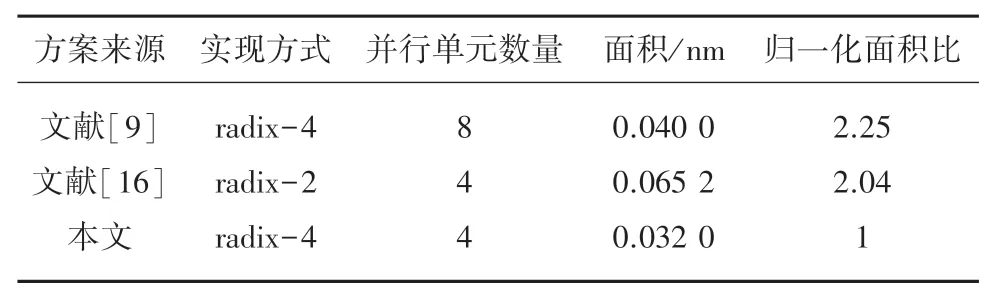
表1 硬件开销对比Tab.1 Hardware overhead comparison

3.2 仿真分析

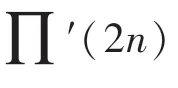
图6 交织地址计算模块输出Fig.6 Interleaved address calculation module output

在交织模块的输出结果基础上，根据式（4）可以计算最终的交织地址，并且将包含正确交织地址Matlab仿真结果读入，仿真结果如图7所示。与FPGA仿真结果进行比对，如果有错误地址输出，则令计数加1。从图7可以看出，每个时钟输出了8路地址，并且没有发生错误，说明本设计可以高效、正确地实现地址交织功能。

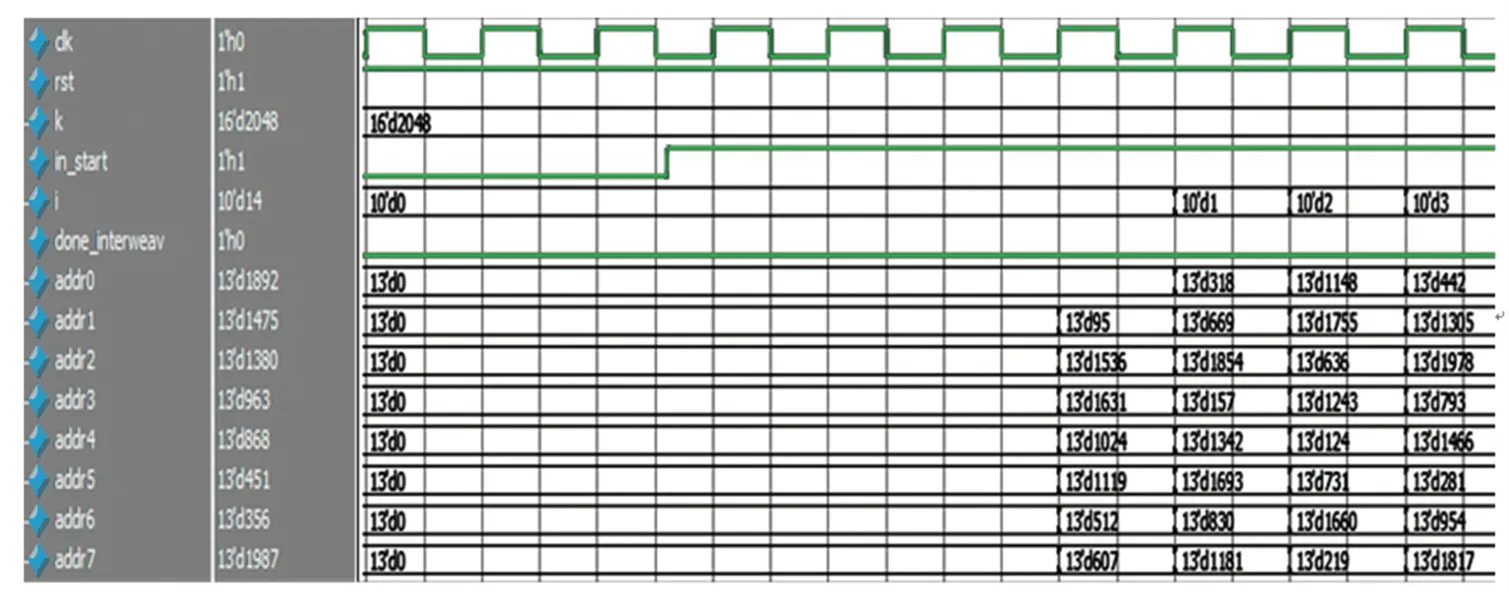
图7 仿真结果Fig.7 The simulation results

4 结束语

本文提出了一种硬件优化的基4四路并行QPP交织器，针对并行计算场景，简化地址递推计算，并消除相邻地址计算的依赖关系，最终可以每个时钟并行输出8路奇偶地址，不仅降低了硬件实现复杂度，也大大提高了地址计算的效率。仿真结果表明本设计硬件开销较小，能够正确地输出交织地址，充分证明了本设计具有可行性。需要指明的是，为了方便QPP交织多项式的递推计算，本文在分块并行译码时，并行块数必须满足＝2，后续可以做进一步优化，将这种并行译码下的递推关系一般化，以方便该并行交织器更好地满足不同场景需求。