InP 中子位移损伤效应的Geant4 模拟*

李薇 白雨蓉 郭昊轩 贺朝会 李永宏

(西安交通大学核科学与技术系,西安 710049)

磷化铟(InP)作为第二代化合物半导体材料,抗辐照能力强,光电转换效率高,在光子领域和射频领域具有优势.大气空间中,InP 半导体器件受大气中子辐照影响,器件性能发生退化.本文采用蒙特卡罗模拟软件Geant4 对InP 中子辐照效应进行模拟,得到InP 中不同能量中子产生的位移损伤初态分布.结果表明:在微米量级内,非电离能量损失(NIEL)随深度均匀分布,在厘米及更高量级上,NIEL 随着入射深度的增大而降低,当靶材料足够厚时可以降低至零;分析1—20 MeV 中子入射3 µm InP 产生的NIEL 及其随深度分布,发现NIEL 随入射中子能量的增加呈现出先升后降的趋势,该趋势主要由非弹性散射反应产生的初级反冲原子(PKA)造成;分析1—20 MeV 中子入射3 µm InP 产生的PKA 种类、能量,发现In/P 的PKA 占比较大,是产生位移损伤的主要因素,中子能量越高,PKA 的种类越丰富,PKA 最大动能越大,但PKA 主要分布在低能部分.研究结果对InP 基5G 器件在大气中子辐射环境中的长期应用具有理论和指导价值.

1 引言

InP 作为重要的第二代化合物半导体材料,禁带宽度大,工作温度高(400—450 ℃),具有高的光电转换效率、高的电子迁移率以及比Si,GaAs 更强的抗辐射能力等优良特性,在光子领域和射频领域具有优势,在固态发光、光纤通信、微波通信、卫星、5G 技术等民用和军事领域前景广阔.

在大气空间中,高能宇宙射线[1]进入地球大气层并与其中的氮(N)、氧(O)等元素发生相互作用,产生次级宇宙射线.由于带电粒子的穿透性较弱,因此大气中存在的粒子主要是中子,称为大气中子[2].InP 材料可能因中子辐射产生晶格缺陷,形成永久性位移损伤[3];也会导致InP 半导体器件发生单粒子效应(SEE),引起单粒子翻转(SEU)、单粒子锁定(SEL)、单粒子瞬态(SET)、单粒子功能中止(SEFI)等多种失效类型[4].通过研究InP材料的中子辐照效应,可以评估其抗辐照性能水平,为器件的选型提供有利依据.

研究材料的辐照损伤效应一般有两种方法.一是实验手段,如电子/质子/离子/中子辐照实验研究;二是计算机模拟.两种方法互为补充.在国外,Inguimbert 和Gigante[5]开发出软件NEMO,通过计算获得电子、质子、中子和重离子等辐照粒子的非电离能量损失(NIEL)[6],尚在不断完善中.Autran等[7]对InP 等8 种III-V 二元化合物半导体的高能大气中子辐射辐照敏感性进行探索.Ruzin 等[8]比较了Si 材料的质子和中子辐照相关性.Messenger等[9]通过对GaAs/Ge 太阳能电池进行辐照实验,使用NIEL 对中子和质子的辐照相关性进行描述.此外,Tonigan 等[10]也对中子和质子辐照相关性进行研究.在国内,蒋维等[11]采用Geant4[12]和FLUKA 模拟软件进行辐照研究,并比较了两种模拟软件在暗物质粒子探测器BGO 量热计中的质子簇射特性.白雨蓉等[13]使用蒙特卡罗方法模拟研究了空间重离子对InP 的位移损伤效应,郭达禧等[14]使用Geant4 模拟软件模拟了中子在SiC 中的输运过程,谢飞等[15]对GaN 材料在不同中子辐照环境下的位移损伤进行了模拟研究.此外,还有有关质子在Si 中[16]、低能质子在Si 和GaAs 中的非电离能损的计算研究[17],以及空间GaAs/Ge 太阳能电池辐照损伤过程的研究[18].但是,中子在InP 中的NIEL 分布情况未见相关报道.本文基于大气中子能谱,使用Geant4 分别模拟不同能量中子辐照InP 后产生的位移损伤效应,包括NIEL 随深度的分布情况,NIEL 与入射中子能量的关系,以及初级反冲原子(PKA)的信息和能谱.

2 计算方法与仿真模型

2.1 大气中子能谱

根据中国散裂中子源(China Spallation Neutron Source,CSNS)提供的第2 靶站微分中子能谱和标准大气中子谱[19],发现大气中子能谱范围非常宽,其中,20 MeV 以下低能中子占绝大多数.又由于辐照损伤中起主要作用的是1 MeV 以上的快中子,所以将入射单能中子能量设置在1—20 MeV范围内,分别为1,2.54,5,8,10,12,14,16,18,19.9 MeV.其中,2.54 MeV 是考虑氘氘(D-D)聚变产生的中子,14 MeV 是考虑氘氚(D-T)聚变产生的中子.

2.2 非电离能量损失

NIEL 是辐照粒子在材料中以位移过程和晶格振动过程沉积的能量,会引起位移损伤,是位移损伤效应的衡量标准.本文通过Lindhard 分离函数计算得到NIEL.

修正Lindhard 分离函数[20,21]如下:

其中,Edam是损伤能,T是初级反冲原子能量,Z1,Z2和A1,A2分别为初级反冲原子与靶原子的原子序数和质量数.对于化合物,原子序数Z2和质量数A2需要加权平均,即

计算得InP 的Z2,average=32,A2,average=72.90.将其代入修正Lindhard 函数中,即可计算得到损伤能Edam.NIEL 与损伤能Edam之间存在线性关系:

其中,ρ是靶材料的密度,h是靶材料的厚度,n是入射粒子数目.通过(7)式可计算得出NIEL 数值.

2.3 可靠性验证

2.3.1 物理过程可靠性验证

中子与InP 晶格原子相互作用,发生弹性散射(n,n)、非弹性散射(n,n′)、俘获反应(n,γ)以及发射带电粒子反应(n,α)(n,p)等,将一部分动能传递给晶体原子,使得晶体原子离开晶格位置成为初级撞出原子,又称初级反冲原子(PKA).高能PKA 继续运动撞击晶体中其他原子,使其离位,产生次级反冲原子,次级反冲原子继续运动撞击其余靶原子,造成一系列级联碰撞,形成原子离位峰.产生空位、间隙原子以及团簇等缺陷.本文采用Geant4 标准物理模型库,包含高精度(n,n),(n,n′),(n,γ),(n,α),(n,p)等基本物理过程.其中,如果PKA 是质子,G4hIonisation,G4Lelastic 和G4CascadeInterface 分别用于模拟电离过程、(n,n)和(n,n′).如果PKA 不是质子,G4ionIonisation和G4BinaryLightIonReaction 分别用于模拟电离过程和核相互作用过程.

ENDF 是由美国国家核数据中心发布的、包含反应堆物理和屏蔽设计所需的核数据库.根据ENDF 提供的In,P 单质的反应截面,采用布拉格相加法则混合得到InP 化合物的反应截面.这种混合方式忽略了化合物中化学键的作用,原因在于化学键的能量远小于粒子能量,不会对结果产生明显的影响.通过比对Geant4 计算得到的弹性散射截面数据与中子评价数据库ENDF 获取的InP 中子截面验证程序的可靠性,截面计算公式为

其中,∆n为单位事件发生弹性碰撞的次数,N为入射粒子数目,h为3 µm 薄靶厚度,I为入射粒子束强度,S为靶横截面积.

图1 为Geant4 模拟结果与ENDF 数据库比对图,两者符合良好,说明本文物理过程模拟结果可靠.此外,这套标准物理模型也经过了其他学者[13,14]验证,结果可靠.

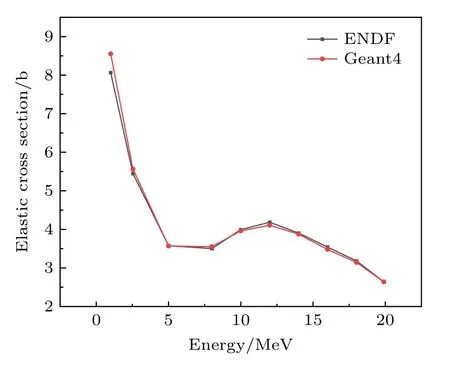
图1 InP 的中子弹性散射截面Fig.1.Neutron elastic scattering cross section of InP.

2.3.2 模拟结果可靠性验证

目前有关中子辐照InP 产生的位移损伤的实验研究还未见详细报道.已有研究[22]给出通过位移比释动能计算得出的1 MeV 中子在InP 中的NIEL 具体数值为0.00064 MeV·cm2/g,该数值与本文用Lindhard 函数计算得出的NIEL 数值0.000526 MeV·cm2/g 进行对比,相对误差为–0.178,在允许范围内,证明本文NIEL 结果具有可信度.

2.4 仿真模型

大气环境中InP 可用作太阳能电池的结构材料,而作为基极的InP 厚度一般为微米量级.因此,参考Walters 等[23]研究中n+p 型InP/Si 太阳能电池中InP 基极的厚度,本文采用3 µm 厚度薄靶作为InP 靶材料.同时,由于中子能量为1—20 MeV,根据平均自由程与宏观截面之间的倒数关系,计算得到中子平均自由程在厘米量级,因此采用3 cm厚靶作为对照,以探究中子对InP 的位移损伤效应.中子沿厚度方向从表面垂直入射到InP 中.结构如图2 所示,外层立方体为world,内层立方体为InP 晶体.

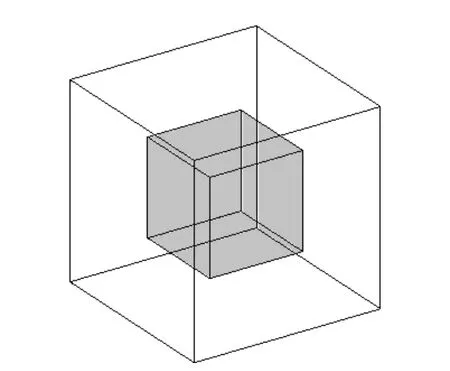
图2 Geant4 模拟的InP 结构图Fig.2.Structure of InP simulated by Geant4.

3 模拟结果分析

3.1 位移缺陷分布

对于3 µm 薄靶,中子从InP 表面垂直入射,入射中子数目均为109;对于3 cm 厚靶,中子同样从表面垂直入射,数目均为107.通过统计PKA 的种类、数目、位置、能量以及NIEL 等信息,探究中子入射InP 产生的位移损伤机制.图3 和图4 为1—20 MeV 中子在3 µm/3 cm InP 中产生的NIEL随深度分布图.

图3 各能量中子在3 µm 薄靶内的NIEL 深度分布Fig.3.NIEL depth distribution of neutrons at different energies in the 3 µm thin target.

图4 (a)各 能量 中子在3 cm 厚靶内的NIEL 深度分布;(b) 1 MeV 中子在3 cm 厚靶内的NIEL 深度分布Fig.4.(a) NIEL depth distribution of neutrons at different energies in the 3 cm thick target;(b) NIEL depth distribution of 1 MeV neutrons in the 3 cm thick target.

从图3 可知,由于3 µm 较薄,中子在3 µm 内碰撞次数少,沉积能量分布均匀.则3 µm 范围内入射深度所导致的NIEL 的差异不太明显,即中子在微米量级InP 中产生的NIEL 与深度无关.

分析图4 可知,当InP 材料厚度增至3 cm 时,NIEL 随深度的增大呈现出缓慢下降的趋势,这表明随着深度的加大,NIEL 逐渐减小.原因在于中子动能因碰撞而不断减小,沉积的非电离能量损失也随之减小.

由于在cm 量级可以观察出NIEL 缓慢减小的规律,因此可以合理外推,当靶厚度继续增加时,NIEL 会继续减小.且由于中子不带电,因此不会出现带电粒子特有的Bragg 峰[24],因此当靶材料足够厚时,中子的NIEL 应当随着深度的增加而单调下降,直至减小为零.为证明这一结论,模拟1 MeV中子从100 cm InP 厚靶表面垂直入射,得到NIEL随深度变化如图5 所示,NIEL 在80 cm 处趋向于0,则结论成立.

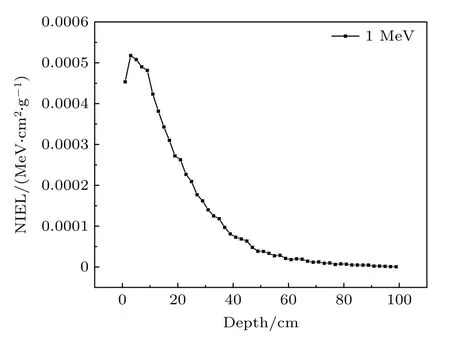
图5 1 MeV 中子在100 cm 厚靶内的NIEL 深度分布Fig.5.NIEL depth distribution of 1 MeV neutrons in the 100 cm thick target.

3.2 位移损伤与入射中子能量的关系

分析1—20 MeV 中子入射3 µm/3 cm InP产生的总NIEL、非弹性NIEL(非弹性散射产生)、弹性NIEL(弹性散射产生)、俘获NIEL(俘获反应产生),比较中子不同反应产生的NIEL,进一步了解中子入射InP 的位移损伤机制.根据Lindhard 分离函数,模拟得到NIEL 与中子能量关系如图6 所示.

图6 NIEL 与中子能量的关系 (a) 3 cm 厚靶;(b) 3 µm薄靶Fig.6.The relationship between NIEL and neutron energy:(a) 3 cm thick target;(b) 3 µm thin target.

分析图6 可知,在1—10 MeV 的入射中子能量范围内,总NIEL 随中子能量的增大呈现上升趋势;10—20 MeV 范围内,总NIEL 呈现下降趋势.原因在于1—20 MeV 范围内,弹性散射NIEL数值在0.0005 MeV·cm2/g 附近波动,入射中子能量造成的NIEL 变化不明显,同时,俘获反应贡献的NIEL 很低,相比之下,非弹性散射造成的NIEL 数值大且变化明显.因此,NIEL 的变化趋势主要由非弹性散射产生的PKA 贡献得到.非弹性散射反应在中子入射InP 的输运过程中占主要作用.

3.3 PKA 的种类、数目及动能信息

1—20 MeV 中子入射3 µm 的InP 薄靶,得到PKA 的种类、数目、动能等信息见表1,PKA数目和入射中子能量的关系如图7 所示,PKA 能谱如图8 所示.

分析表1 可知,1—20 MeV 中子入射InP 产生的PKA 中,In/P PKA 占绝大多数,其中,In 元素占比高于P 元素,原因在于In 的中子反应截面大于P,则In PKA 数量多.随着中子能量的增加,PKA 种类越来越丰富,且每种元素对应的同位素种类也越来越丰富,In/P PKA 总占比逐渐下降,其他PKA 占比增加.原因在于中子能量越高,核反应种类越多,则反应产物增加,主要包括113—116In(n,p)113—116Cd,113,115In(n,α)110,112Ag,30,31P(n,p)30,31Si,30,31P(n,α)27,28Al 等反应产生的Cd等新核以及反冲出的H,He 等PKA.比较PKA最小和最大动能可知,随着入射中子能量的增加,PKA 的能量范围也逐渐扩大.

表1 1—20 MeV 中子入射3 µm 的InP 薄靶所得PKA 的种类、数目与动能信息Table 1.The type,number,and energy information of PKA obtained from 3 µm InP thin target irradiated by 1—20 MeV neutrons.

图7 为1—20 MeV 中子入射3 µm InP 产生的不同种类PKA 占比图,主要统计了总PKA,In PKA,P PKA,其他元素PKA(H,Si,He,Al,Cd等).分析图7 可知,In PKA 占比大,与总PKA 变化趋势相同,是产生位移损伤的主要因素.

图7 1—20 MeV 中子入射3 µm InP 产生的不同种类PKA 数目Fig.7.The number of different PKA produced by 1–20 MeV neutrons incident on 3 µm InP.

图8 为1—20 MeV 中子入射InP 产的PKA能谱图,分析可知,PKA 动能主要分布在低能部分,原因在于中子质量远小于靶核质量,传递给反冲核的能量很低.高能PKA 主要是质子和α.

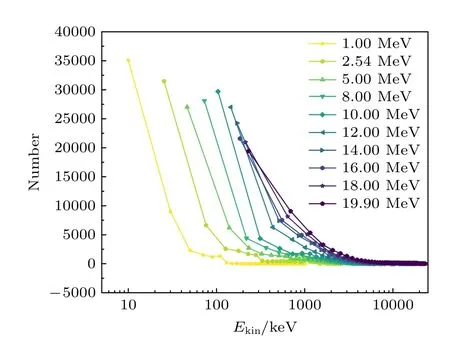
图8 1—20 MeV 中子入射3 µm InP 的PKA 能谱Fig.8.The energy spectrum of PKA produced by 1–20 MeV neutrons incident on 3 µm InP.

综上所述,1—20 MeV 中子入射InP,主要产生In/P PKA,其中In PKA 占比大,是导致位移损伤的主要因素.同时,当中子能量逐渐增大时,PKA 的种类越来越丰富,最大动能也随之增大,但PKA 能量仍主要分布在低能部分.

4 结论

通过Geant4 模拟了1—20 MeV 范围内不同能量的中子入射InP 半导体材料的位移损伤效应,得出结论如下.

1) 在微米量级内,NIEL 随深度均匀分布;在厘米及更高量级上,NIEL 随着入射深度的增加而降低,当靶材料足够厚时可以降低至零.

2)分析1—20 MeV 中子入射3 µm InP 产生的NIEL 及其随深度分布,发现NIEL 随入射中子能量的增加呈现出先升后降的趋势.该趋势主要由非弹性散射反应产生的PKA 造成.

3) 分析1—20 MeV 中子入射3 µm InP 产生的PKA 种类和能量,发现In/P 的PKA 占比较大,是产生位移损伤的主要因素;中子能量越高,PKA 的种类越丰富,PKA 最大动能越大,但PKA主要分布在低能部分.