用于磁旋转光谱的环形永磁阵列的匀场分布仿真优化*

贾丰鸣 梅教旭 王瑞峰 程刚 刘锟 高晓明

1) (中国科学院合肥物质科学研究院,安徽光学精密机械研究所,合肥 230031)

2) (中国科学技术大学,合肥 230026)

3) (安徽理工大学,深部煤矿采动响应与灾害防控国家重点实验室,淮南 232001)

法拉第磁旋转光谱(Faraday rotation spectroscopy,FRS)技术因其高灵敏度,零背景噪声,以及能有效避免抗磁性物质干扰的特性广泛应用于各类顺磁性痕量气体的探测.目前大部分FRS 技术采用线圈构造电磁场,存在能耗高、发热多等问题.为此,开展了基于组合环形永磁体的空间磁场分布建模仿真研究,意在建立轴向分布的磁场,为测量FRS 提供基于永磁体的沿光轴方向的匀强磁场.仿真采用有限元网格剖分的方法,基于麦克斯韦方程组,开展组合磁环的磁场分布仿真研究,并通过实验测量实际钕铁硼永磁体磁环阵列的磁场分布,证明了建立物理模型的可靠性.在此基础上提出了对永磁体磁环阵列的3 种优化方案—单理想值优化、多段式单理想值优化和梯度优化方案,来构造中心轴线磁感应强度分布均匀的匀强磁场.最后通过引入磁场均匀度,计算评估并分析比较了不同优化方案的优化效果,为研发基于永磁体的FRS 光谱设备提供参考.

1 引言

法拉第磁旋转光谱(Faraday rotation spectroscopy,FRS)是以分子吸收线在磁场的作用下发生Zeeman 效应,从而引起磁致双折射效应为基本原理[1,2],基本原理图如图1 所示.激光通过起偏器变成线偏振光并通过轴向磁场,当在沿光轴的磁场中存在顺磁性分子时,分子的能级由于Zeeman 效应而对称地分裂为多个Zeeman 子能级.其中满足∆MJ=+1和 ∆MJ=−1 的跃迁选择定则的能级分别吸收右旋圆偏振光和左旋圆偏振光,由于不同旋向的圆偏振光在介质中的折射率不同,从而产生磁致双折射效应.线偏振光是右旋圆偏振光和左旋圆偏振光的叠加态,所以线偏振光在沿光轴的磁场中通过一段距离为L的顺磁性分子样品池时,由于磁致双折射效应,它的偏振面将产生角度为φ的偏转.在样品腔后放置检偏器,通过光电探测器可探测因磁致双折射效应而发生偏振面偏转的透射光强,其强度与样品浓度成正比关系,通过标定可实现文献样品[3−浓5度].的检测分析.详细的FRS 理论可参考

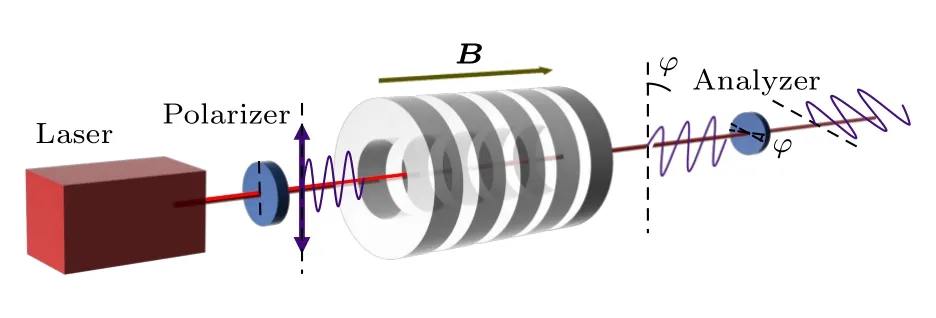
图1 FRS 原理示意图Fig.1.Schematic diagram of FRS.

相对于传统的吸收光谱,FRS 因其对光的偏振态敏感,故对顺磁性分子具有更高的灵敏度和选择性,可以有效降低光源噪声,而且不受非顺磁性分子的干扰,尤其是不受H2O 和CO2分子的干扰,这大大提高了FRS 探测大气顺磁性分子的选择性[1],可广泛用于多种顺磁性痕量气体的探测,如NO[6−15],NO2[1,16,17],O2[18,19]和OH 自由基[20]等.

目前大部分FRS 技术采用线圈电磁方式进行.例如,Smith 等[16]报道了FRS 高灵敏度探测NO,其通过给线圈提供3.5 A 的电流,产生了110 G(1 G=1×10–4T)的磁场,探测灵敏度达到了4×10–9(体积比,后文无特殊说明均指体积比),并应用于2008 年的北京奥运会;Zaugg 等[17]采用FRS实现了NO2的高灵敏度探测,采用7 A,832 Hz 的交流电,产生了230 G 的轴向磁场,达到了1×10–9的探测灵敏度.在文献[1]中为产生200 G 的轴向匀强磁场,工作电流为5 A 的交流电,对NO2的探测灵敏度达到2.5×10–9.这种正弦交流电产生磁场的方法存在能耗高和发热多的局限性.为此,赵卫雄等[20]开展了基于超导线圈的FRS 技术研究,采用由NbTi 超导材料制成的线圈,用循环低温冷却器和He 将线圈冷却至5 K 以下,以达到超导状态,通电电流12 A,产生的磁场磁感应强度为215 G.这种采用超导电磁的FRS 克服了线圈发热的问题,能够产生较高的磁场,但涉及超导的液氦制冷,仅适用于实验室的分析研究,基于目前的超导技术水平,对发展便携式的FRS 设备有一定的局限.针对线圈电磁的问题,2012 年,Brumfield 等[18]开展了基于永久磁铁的FRS 探测O2的研究,其采用由20 个圆柱状稀土磁体组成的八极磁体排列结构,构造了在110 mm 长度内磁感应强度为554 ±64 G 的磁场,最终实现了1.3×10–9的灵敏度.

从以上文献分析可知,目前大部分FRS 以正弦调制的线圈电磁的方式实现,虽然少量开展了基于永磁体磁场的FRS 实验,但对永磁体磁场的优化设计方面开展讨论和研究的还比较少见.FRS的核心组件之一就是磁场,而磁场的强度、均匀性和有效长度很大程度上会影响FRS 系统的性能和检测灵敏度.因此,探索研究永久磁场的构建具有重要的理论研究意义和应用价值.为此开展了基于环形永磁体阵列构建适用于FRS 的仿真优化研究,以便通过永磁替代电磁,降低能耗,提升磁感应强度.论文研究对发展低能耗、高性能的FRS 仪器具有重要的参考价值.本论文提出的仿真优化方法,也可通过适当的调整应用于其他需要匀强磁场的应用中,如激光陀螺中法拉第云室的构建[21],微波电子器械中的磁路设计等.

2 磁场设计理论依据

为了说明磁场磁感应强度和有效长度对FRS探测信号的影响,以及构造适用于FRS 装置的均匀强磁场,首先对FRS 基本的理论做简要介绍.

入射的线偏振光通过磁场中的气体分子后,偏振面会旋转一个角度φ,称为Faraday 旋转角,可表达为[8]

式中,n±分别是右旋圆偏振光(+)和左旋圆偏振光(–)的折射率,const(n+−n−) 的大小和顺磁性分子的浓度成正比,B是外磁场的磁感应强度,L是入射线偏振光和磁场中气体分子相互作用的程长.对于气体分子,该旋转角非常微小,为了使该旋转角可测量,故适当增加磁场的磁感应强度和长度来增大Faraday 旋转角,从而探测到FRS 的信号.同时,从检偏器探测到的FRS 的出射信号强度I可表达为[8]

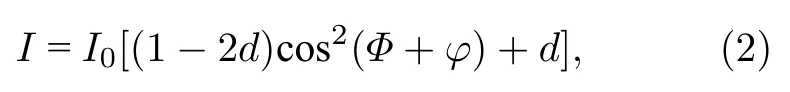
其中,I0为入射光强度,d为两个正交偏振片的消光比(最大为 10−5),Φ为两个偏振片偏振轴之间的夹角.由(2)式可知,Faraday 旋转角的大小对最终探测到的FRS 的信号强度有重要影响.

对于FRS 的性能而言,磁场强度和分布的长度是提升FRS 性能的关键环节之一,因此开展磁场构建的研究对FRS 至关重要.论文以磁环的物理模型为基础,提出单理想值优化、多段式单理想值优化以及梯度优化的永磁体磁环阵列优化方案,并运用计算机仿真建模手段分析各类方案的磁场特性.

3 磁环物理模型建立

根据第2 节理论可知,构建不同强度和长度的匀强磁场将获得不同的信号效果.为此本文采用多个永磁体磁环组合的方式,通过优化磁环的排列间距和磁环的磁化参数,来实现满足FRS 测量的磁环阵列的优化方案,为FRS 的磁场构造提供参考.

首先,构建正确的磁环物理模型.对实验室现有的磁环封装进行测量,该封装由5 个型号为N52的钕铁硼磁环组成,相邻磁环以7.70 mm 的间距隔开,磁环的内径为60 mm,外径为100 mm,高度为25 mm,剩磁1.42 T,矫顽力Hcb=828—907 kA/m,内禀矫顽力Hcj≥ 876 kA/m,最大磁能积 (BH)max=394—414 kJ/m3,工作温度≤ 70 ℃(宁波磁性材料厂出厂数据提供).将磁环组放置在无磁性的实验平台上,将高斯计的探头固定于滑轨上,通过探头在滑轨上滑动的方式测量磁环组中心轴线的磁感应强度分布,每隔5 mm 读取高斯计测量值,所得中心轴线的磁感应强度分布如图2 所示.

图2 实验测量结果Fig.2.Measurement result of experiment.

接下来对该封装的磁环进行仿真建模.用于磁环物理模型构建的磁化模型有很多种,如相对磁导率,磁损耗,B-H曲线,等效B-H曲线,剩余磁通密度,非线性永磁体等.考虑到厂家提供的参数和钕铁硼材料的属性,采用剩余磁通密度Br作为永磁体磁环的磁化模型,基于Br建立永磁体磁环空间磁场B-H的本构关系,其中B为磁感应强度,也称磁通密度,H为磁场强度,且两者满足

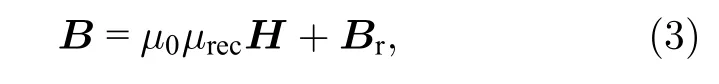
式中µrec为回复磁导率,µ0为空气磁导率;Br=为剩余磁通密度模,由材料属性决定;e是剩余磁通密度的方向矢量,取e=(0,0,−1).结合∇×H=J,B=∇×A,J=σE可以得到永磁体等效的电流密度,用磁通密度z分量表征磁体轴向磁场的空间分布特征.

因钕铁硼永磁体的典型回复磁导率µrec=1.05,与空气的相对磁导率µair=1.00 接近,故多磁环组的磁场分布可视为多个单磁环的磁场的线性叠加[22].采用二维建模对磁环组进行仿真分析,在旋转轴右侧距离旋转轴30 mm 的位置构建宽20 mm,高25 mm 的小矩形,该小矩形代表磁环轴向截面的二分之一.将矩形沿z轴方向阵列,位移为32.5 mm(矩形高度25.0 mm+间隔7.7 mm),最终得到等间距排列的5 个小矩形(第4 节对该对称模型有详细叙述).以旋转轴为一条边,构建一个宽为 200 mm,长为600 mm 的大矩形作为磁环所处的空间,并在该矩形的顶部、底部和右侧设置厚度为20 mm 的边界层,并定义该边界层为无限元域,其构建可保证磁环在大矩形空间中的磁场分布不会因为边界限制受到影响;采用内置的空气材料对整体(小矩形和大矩形)进行填充;对代表磁环的小矩形,采用安培定律和B-H本构关系对小矩形进行磁化,为保证所得磁环中心轴线磁感应强度是正值,以z轴负方向为磁化方向.设置磁环的初始磁通密度为1.42 T (基于厂家提供的Br=1.42 T),仿真过程中发现测量结果与仿真结果存在偏置,调整Br=0.9 T 时,两者吻合最好,最终确定建立模型∥Br∥=0.9 T .偏置的原因是永磁体的磁路中有空隙,因此永磁体的实际工作点在退磁场的作用下由Br点移至退磁曲线上的某点,使永磁体的剩磁不再是Br[23],故仿真所用的Br需进行适当调节.基于有限元求解方法的流程,对模型进行自由网格剖分,得到的三角形网格单元数为635,四边形单元网格数为260,共计628 个网格顶点,34 个顶点单元且最小单元质量为0.63020,平均单元质量为0.89710,单元面积比为0.02374;对计算结果进一步整理,采用二维旋转得到三维空间的磁感应强度分布结果,通过设置磁环轴向截面观察磁场分布状况,组合永磁体磁环的磁感应强度分布截面图如图3 所示.图3(a)中箭头方向表示磁感应强度方向,图3(b)中的流线代表磁力线.

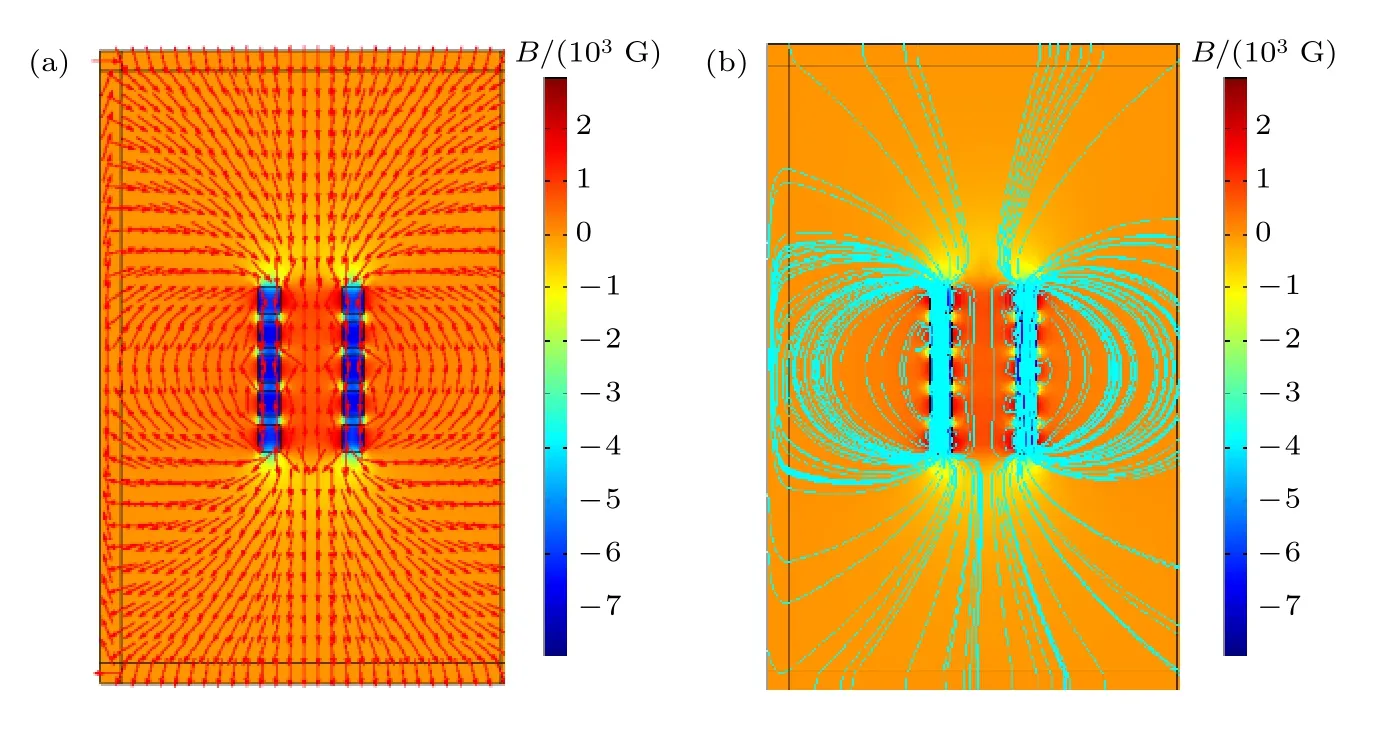
图3 永磁体磁环阵列仿真效果图 (a) 磁感应强度分布特征箭头图;(b) 磁感线分布特征流线图Fig.3.Modeling magnetic induction of array-ring permanent magnets:(a) Arrow distribution of magnetic induction intensity;(b) streamline diagram of magnetic induction.

为与实验测量结果保持相同的精度,设置的域点探针也每间隔5 mm 提取中心轴线的磁感应强度z分量,导出域点探针的数值,磁环中心轴线磁感应强度和实验测量结果的比较如图4(a)所示,误差棒表示实验值和测量值之差,即测量值的误差.磁环阵列总长156.4 mm,取磁环阵列中间点z1=78.20 mm(扫描路径1)和第二个间隔中间点z2=61.64 mm(扫描路径2)处的径向磁场磁感应强度分布绘制成图4(b).可以看出,两条曲线都沿中心呈对称分布,差别在于磁环体的径向磁感应强度分布呈中间低两侧高的趋势,但间隔处的径向磁感应强度分布呈中间高两侧低的趋势,两个图线的变化呈相反的趋势.这种差异是因为磁环体内的磁场远大于它所处空间的磁场的磁感应强度.

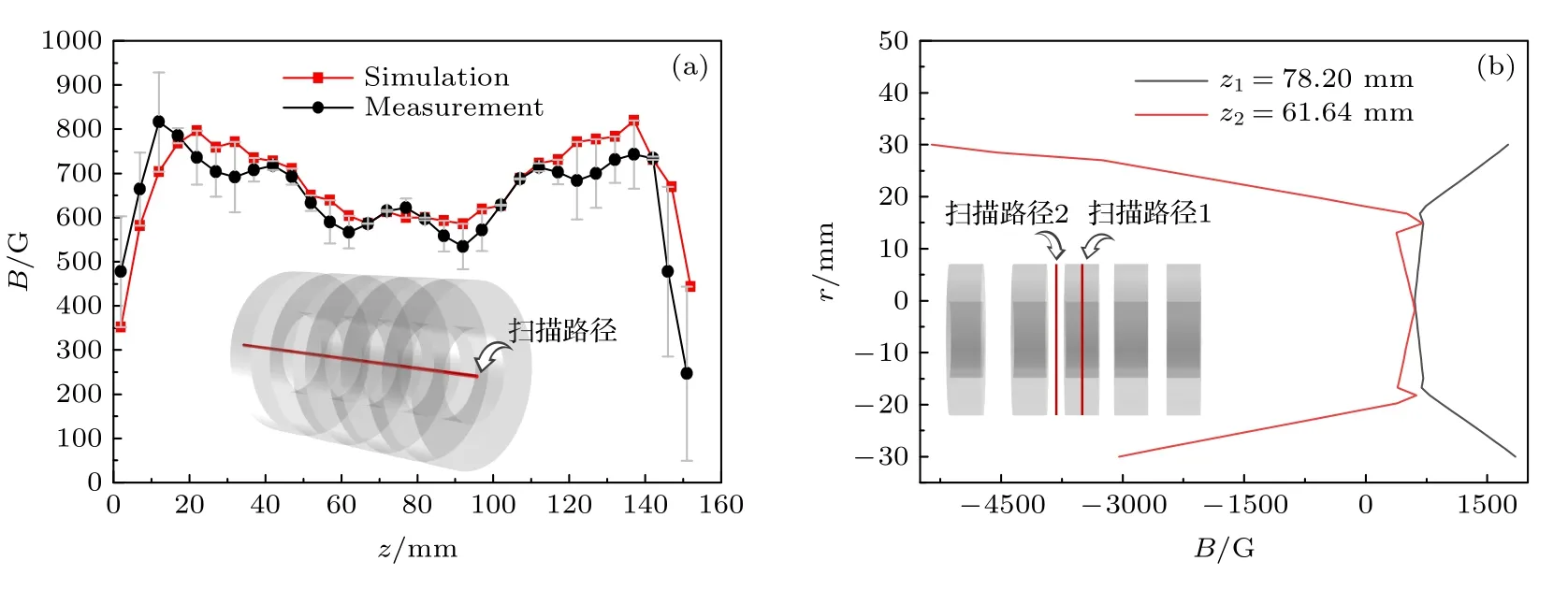
图4 五个磁环的实验与仿真结果 (a) 实验与仿真结果对比图;(b) 磁环体内部(z1=78.20 mm)和间隔(z2=61.64 mm)处的径向磁感应强度分布图Fig.4.Measurement and simulation results of five magnetic rings:(a) Comparison of experimental and simulation results;(b) radial magnetic induction intensity distribution inside the ring (z1=78.20 mm) of the group and gap (z2=61.64 mm).

图4(a)为磁环中心轴向磁场磁感应强度z分量的理论仿真和实验测量结果,两者相关性为0.838.偏差主要有以下原因:1) 实际磁环的尺寸(内外径,高度)与仿真模型有误差;2) 无法保证实际磁环的剩余磁化参数(Br)处处均匀;3) 磁环的排列间距并非完全相等,使得实际测量的磁环间隔处的空间磁场分布与仿真有一定的误差;4) 滑轨上探头位置的测量和读取误差也需考虑在内.考虑到这些误差因素,结合实验测量与仿真结果的相对误差,可以认为所建物理模型是可靠的,可用于磁环组的磁场分布优化研究.

4 优化方案

为了最大程度地减少求解模型所需的计算资源和时间,提高运算效率,对磁环组的解析建模过程进行了优化.研究过程中利用永磁体磁环的对称性质对模型进行简化.采用二维轴对称构图对多个磁环组成的磁环阵列进行建模,将对称边界定义为理想磁导体边界,该边界条件代表等效电流的镜像对称平面.因磁场方向和电场方向垂直,磁场垂直穿过理想磁导体边界,而电场则与理想磁导体边界平行.在对称平面的另一侧,等效电流将被精确镜像,即等效电流仍沿切向流动,且方向不发生变化,也不会出现法向分量.故永磁体的磁场可由等效电流的分布情况根据本构关系计算得出.且磁环磁场具有空间分布的对称性,圆环具有旋转对称性,故采用二维轴对称模型对永磁体磁环组进行建模.模型建立过程如图5 所示.基于磁环组的二维轴对称模型,采用有限元方法对磁环组的排列间距和所需磁环个数进行仿真计算.

经过比较分析,采用内径180 mm,外径220 mm,高度25 mm 的磁环进行三种优化方案的比较.在旋转轴右侧距离旋转轴90 mm 的位置构建宽20 mm,高25 mm 的矩形,小矩形代表磁环轴向截面的1/2.在旋转轴右侧距离旋转轴70 mm的位置构建宽60 mm,高27 mm 的矩形,作为磁环优化的移动变形区域1.将上述两矩形沿z轴方向阵列,位移为S0=45 mm (矩形高度25 mm+初始间距20 mm)最终得到等间距排列的6 个嵌套的矩形.在旋转轴右侧距离旋转轴86.5 mm 的位置构建宽27.0 mm,高350.0 mm 的矩形,作为变形区域2,并且使变形区域1 和2 的交叉部分为一个正方形且恰好嵌套着小矩形.在旋转轴右侧距离旋转轴70 mm 的位置构建宽60 mm,高350 mm的矩形,作为变形区域3,是整个磁环的优化区域,包含变形区域1 和2,以及所有小矩形.以旋转轴为半径所在位置,构建一个半径为450 mm 的1/4 圆作为磁环所处的空间,并设置厚度为30 mm的边界层,并定义该边界层为无限元域.变形区域的划分和网格剖分示意图如图6 所示.

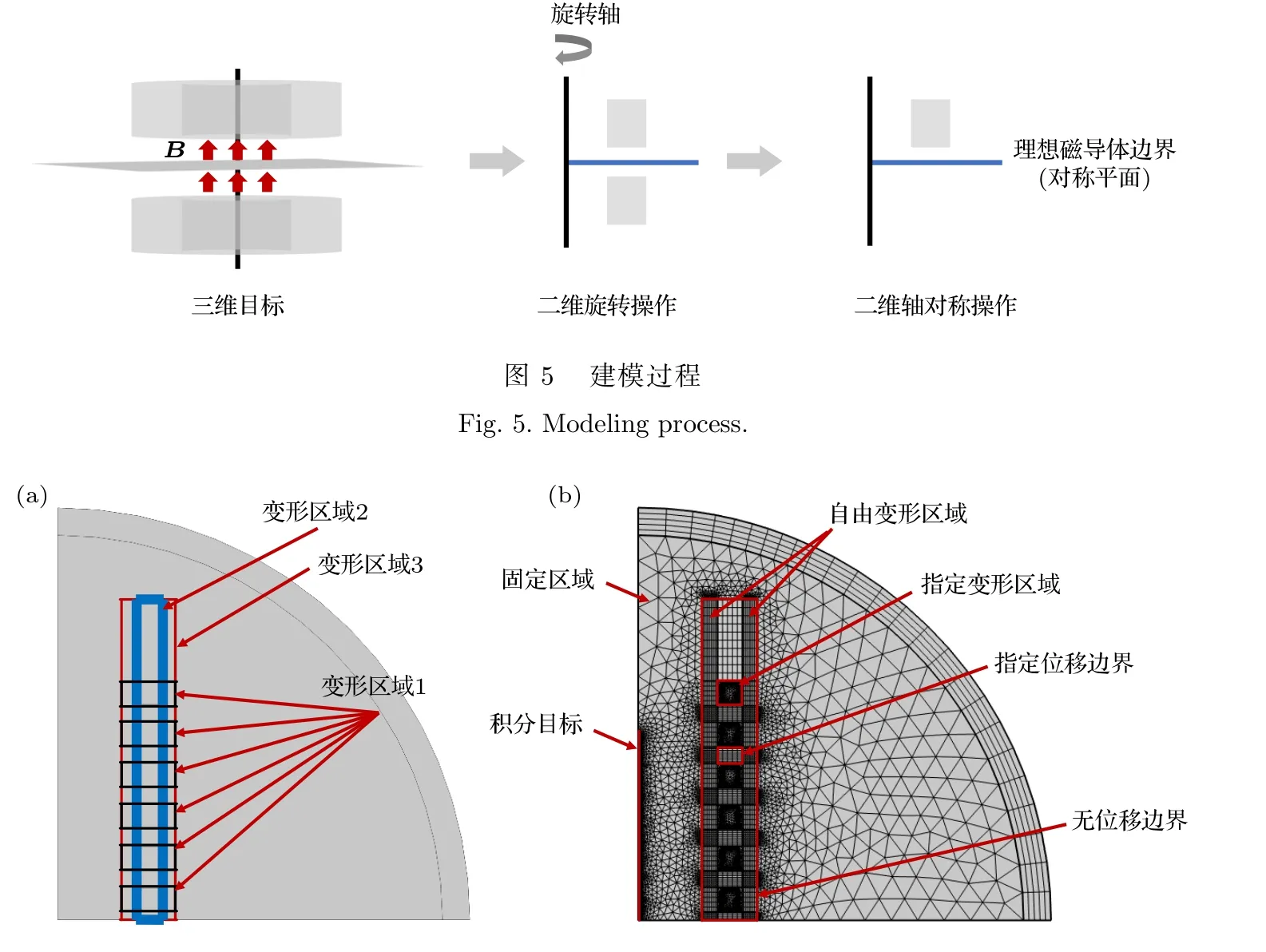
图6 有限元仿真区域网格剖分 (a) 变形区域的划分;(b) 间距优化网格剖分图Fig.6.Deformation and meshing division of finite element simulation:(a) Division of deformation zone;(b) gradient optimization mesh division diagram.

用内置的空气材料对整体(6 个小矩形和1/4圆)进行填充;采用安培定律和B-H本构关系对小矩形进行磁化,为保证所得磁环中心轴线磁感应强度是正值,以z轴负方向为磁化方向,剩余磁通密度模取值为0.9 T;截取旋转轴上z=0 mm 到z=200 mm 的一条线段,作为优化算法的积分目标.(4.1 节—4.3 节提到的三种优化算法均基于SNOPT 非线性求解器进行优化计算.三种优化目标表达式后文将详细叙述,且优化目标是本论文讨论的重点.)为避免优化过程中出现磁环相交的情况,每个磁环可移动的距离的上下限需有边界条件限制,磁环可移动范围的边界约束条件为

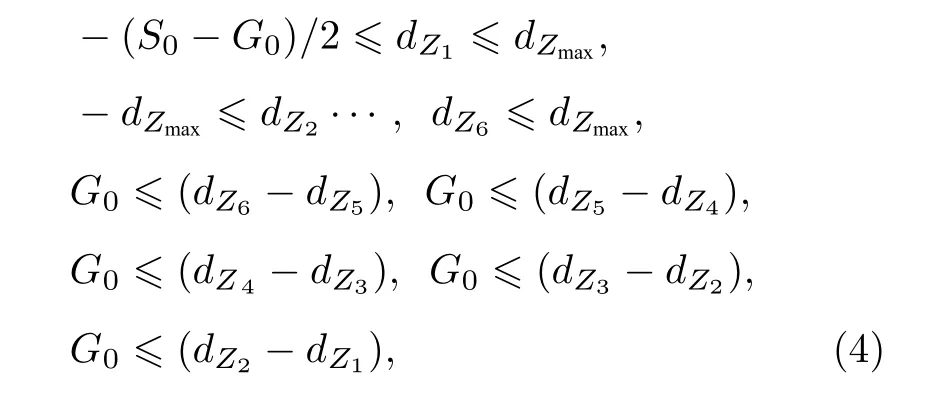
采用双线插值法计算变形区域边界的Laplace 方程的解[24],对于不同的建模区域以及复杂的边界约束条件如固定区域、自由变形区域、指定变形区域、指定位移边界、无位移边界等,需要对边界进行特殊的网格剖分.网格剖分图如图6(b)所示,其中三角形网格单元数为67141,四边形网格单元数为2350,边单元为5255,最小单元质量为0.1886,平均单元质量为0.842,单元面积比为2.036×10−6.共计有边单元5255 个,顶点单元86 个,网格面积1589 cm2.下面基于以上网格剖分方案,进行三种优化方案的研究和讨论.

4.1 单理想值优化

单理想值优化方法,即将中心轴线的磁场磁感应强度的z分量Bz与目标值B0之间的差异最小化,并沿磁环中心从z=0 到z=L0进行积分.为使目标函数的值收敛,该目标值相对于L0是归一化的:

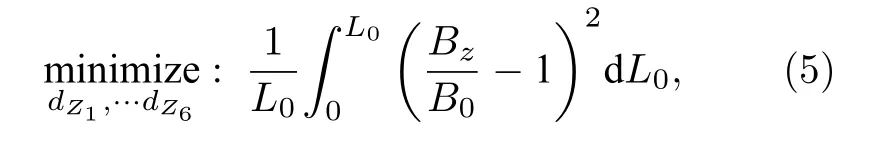
其中L0为目标磁场的长度,此处取L0=20 cm ;B0为目标磁场磁感应强度的理想值,此处B0=0.024 T(240 G).

图7 单目标值优化中心轴向磁感应强度分布Fig.7.Single value optimization of central axial magnetic induction.

最终优化结果如表1 所列(位移量为正,磁环上移;位移量为负,磁环下移),结合磁环的初始间隔,可计算出相对于对称边界,磁环的排列间距(见表2).

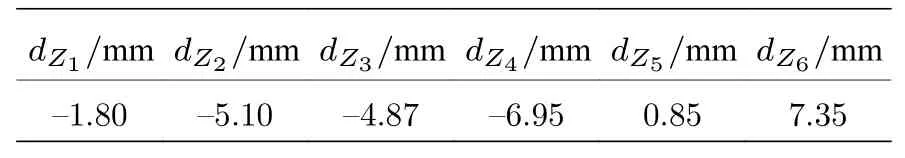
表1 单理想值优化结果Table 1.Results of single-objective optimization.

表2 单理想值优化磁环排列间隔Table 2.Magnetic rings gaps of single-objective optimization.

设置域点探针,用于提取中心轴线磁感应强度z分量的数值,每隔0.01 mm 读取一次探针数值,绘制成中心轴向磁感应强度分布图(图7),数据提取的扫描路径如图8 所示.与表2 参数相对应的,磁环组的间距排布见图8.

图8 磁环组分布情况Fig.8.Distribution of magnetic ring arrangements.

4.2 多段式单理想值优化

基于对单理想值优化方案的讨论,发现目标磁场的优化结果仍有较大的不均匀分布,为了减小这种不均匀程度,采用多个理想值,对目标磁场区域分段优化,称为多段式单理想值优化方案.在多段式单理想值优化分析中,对磁环中心均匀分布的5 个点进行理想值约束,其中受约束的点依次为z=0,5,10,15,20 cm.即采用多段式单理想值将磁场轴向分量与各理想值之间的差异最小化,将Bz沿磁环中心从1,2,3,4)进行积分.为了使函数目标值收敛,目标相对于是归一化的,且满足

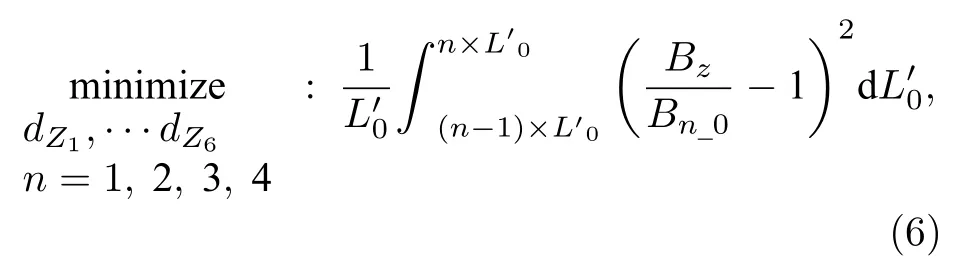
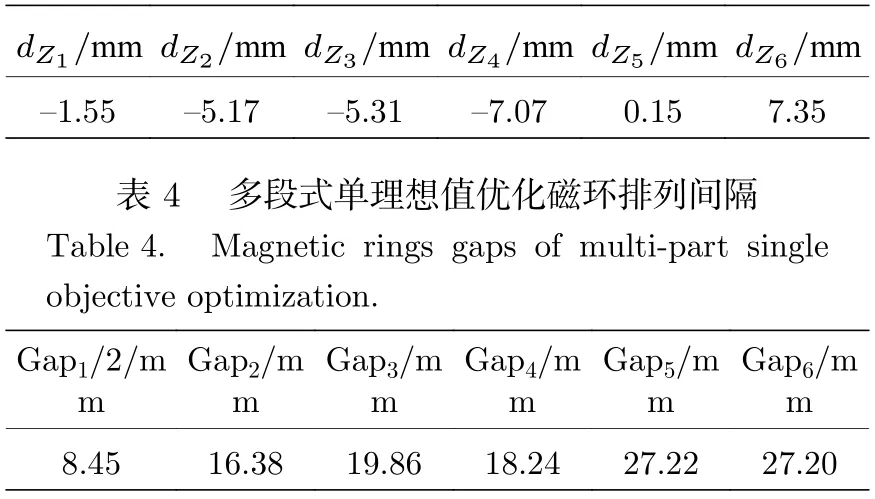
表3 多段式单理想值优化结果Table 3.Results of multi-part single objective optimization.

设置域点探针,用于提取中心轴线磁感应强度z分量的数值,为保证和单理想值优化结果的精度相同,依然每隔0.01 mm 读取一次探针数值,绘制成如图9 所示的中心轴向磁感应强度分布图.

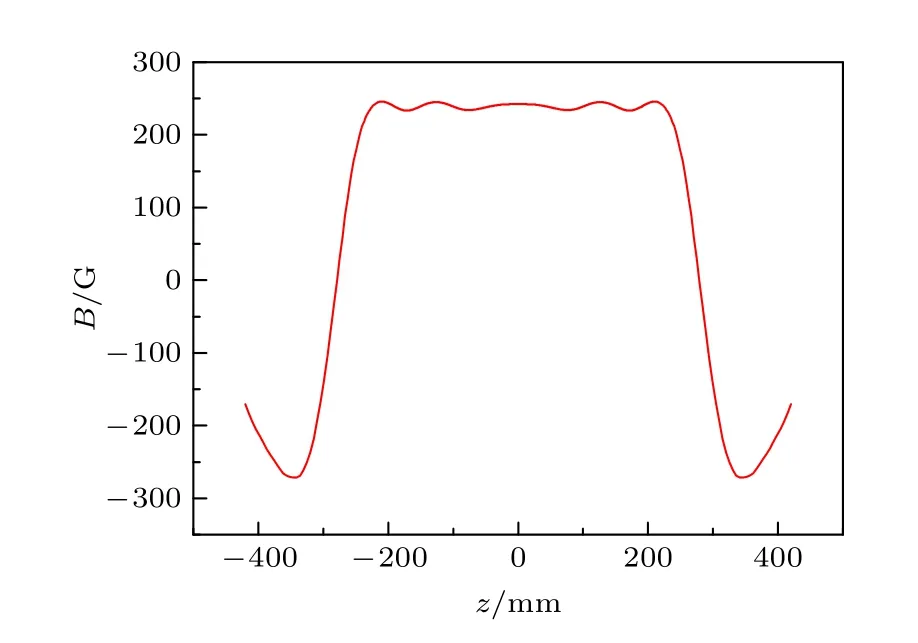
图9 多段式单理想值优化中心轴向磁感应强度分布Fig.9.Multi-part single objective optimization of central axial magnetic induction.

为比较两种优化方案,用200 mm 目标磁场磁感应强度的方差衡量磁场均匀程度,称为磁场均匀度参数ζ,每间隔0.01 mm 取磁感应强度数值,共取20000 个中心轴线处的磁感应强度z分量值Bz_n,用于计算中心轴线磁场均匀度,其表达式为

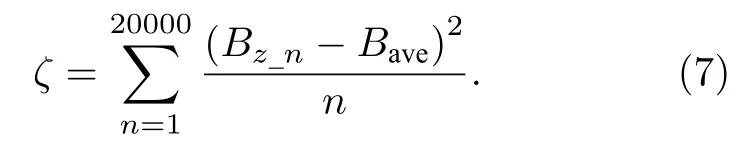
式中,Bave为由20000 个中心轴线磁感应强度计算出来的平均值.对于单理想值优化,磁场均匀度ζ=23.2359;多段式ζ=12.7926 .此结果表明,相比于单理想值优化的磁场均匀度,多段式提高了44.9%,说明多段式单理想值磁场优化效果相比于单理想值优化效果好,但是该磁场均匀度仍不足以满足均匀磁场的要求.

4.3 梯度优化

针对前面单理想值优化、多段式单理想值优化构造的磁场均匀度有限的问题,结合多段式单理想值优化的优化方案能显著提升磁场均匀度的特点,对优化方法进行了进一步的改进,提出了梯度优化方法,即基于对磁场中心轴线方向的磁感应强度梯度进行二次积分作为优化目标,并进行归一化处理,研究讨论该情况下的局部最优解,

其中L0=20 cm,B0为目标磁场磁感应强度的理想值,此处定义B0=0.024 T,Bz为轴向磁场的z分量.考虑最小化沿优化区域的磁场梯度,在需要构造的匀强磁场的中心点对场进行约束.优化方程通过取轴向磁感应强度的z分量,并计算z方向梯度的平方值,之后将所得表达式对磁场长度进行积分,并用L0B0对前式进行归一化运算,这一过程可表示为(8)式.

表5 梯度优化结果Table 5.Results of gradient optimization.

设置域点探针,用于提取中心轴线磁感应强度z分量的数值,每隔0.01 mm 读取一次探针数值,绘制成如图10 所示的中心轴向磁感应强度分布图.

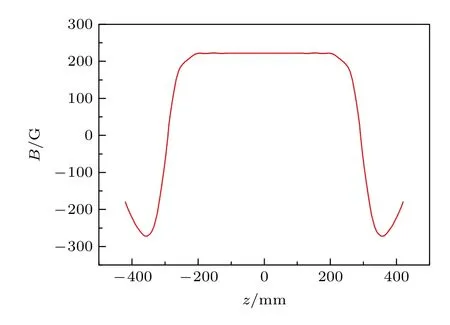
图10 梯度优化中心轴向磁通密度分布Fig.10.Gradient optimization center axial magnetic flux density distribution.

为方便对以上三种方案的优化结果进行比较,均采用(7)式计算三种优化结果的磁场均匀度,最终结果见表7.

表7 三种优化方案的磁场均匀度结果比较Table 7.Comparison of magnetic field uniformity of three optimization method.

相比于均匀缠绕的螺线管产生的均匀磁场,想要用永磁体磁环产生匀强磁场,需将磁环阵列进行不等间距的排列.这样的排列方式是由磁环本身的空间磁场分布特性决定的.单个磁环中心轴线上的磁场分布并非处处相同,且对于不同规格尺寸的磁环,尤其是磁环轴向长度的取值,会使中心轴线上的磁场呈现一定程度的不均匀性.这个特点和永磁体退磁场的不均匀性质相关.

等间距排列的磁环中心轴线的磁场分布显示(见图2),磁环阵列的中心区域出现了大幅衰减.磁环实际的空间磁场分布情况与磁化场和磁体本身的退磁场两部分相关,且退磁场的方向与外加磁化场方向相反.永磁体的实际工作点将从剩磁点移动到磁滞回线的第二象限,即退磁曲线上的某一点.因此永磁体的空间磁场分布应采用退磁曲线上的物理量来描述.退磁场的强度Hd与磁体的几何形状和磁极的强度M有关,且满足关系Hd=−αM,其中α称为退磁因子,仅与材料的形状有关,且与磁化方向的轴长度成反比.如对于沿长轴方向磁化的细长样品,α接近于0,但是对于短而粗的样品,α可以很大.仅少数几何形状的样品能计算退磁因子,比如椭球体,球体,细长圆柱体等.对于环状物体的退磁因子,还无法准确数值计算[23].由此,磁环的实际空间磁场分布大多由仿真或实际测量来表述.论文旨在给出适用于磁环优化的一般性解决方案,但对于不同永磁材料和规格的环形永磁体,还需根据实际情况进行优化方案的选取和参数的调节.

5 结论

构建了正确模拟永磁体磁环空间磁场分布的物理模型,首先利用微位移平台测量了实验室5 个磁环样品中心轴线上的磁感应强度的分布,并对5 个钕铁硼磁环组进行仿真建模,实验测量与仿真结果相关性较强,证明了基础物理模型的构造正确;基于间距调整的有限元网格剖分方案,采用三种优化方案构建了三类优化模型:单理想值优化方案,多段式单理想值优化方案,梯度优化方案.由于以上方案返回的结果均为局部最优解,故在优化参量相同的情况下,所得结果也不尽相同.单理想值优化方案基于磁场轴向分量与理想值之间的差异最小化为原则,对中心点处的磁通密度值进行约束.为进一步探索理想值优化的局部最优结果,提出多段式单理想值优化方案,采用多个理想值,分别对总目标磁场的不同区域磁场进行理想值优化,所得优化方程的目标值优于单理想值方案,即此种方案的优化结果优于单理想值优化结果.基于以上分析研究,将优化区域无限细分,即做微元处理后再积分,提出梯度优化方案.该方案的优化结果比其他两种方案低3 个数量级,说明优化的磁场均匀性明显高于另外两种方案.根据本论文的仿真分析,发现在磁环高度和内外径差保持不变的情况下,同时大幅度增加磁环的内外半径,更有利于构建均匀强磁场.论文为FRS 光学谐振腔采用永磁体磁环阵列构造均匀强磁场的设计方案提供了参考和借鉴.从而替代电磁方式,构造出能够长时、稳定工作的无能耗磁场,可以为发展FRS 检测技术和应用研究提供参考.