具阻尼广义Korteweg-de Vries 方程的迭代学习控制*
2022-04-27范雄梅
火力与指挥控制 2022年3期
明 森,李 霞,范雄梅
(1.中北大学数学系,太原 030051;2.中北大学大数据学院,太原 030051)
0 引言
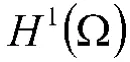
经典的KdV 方程描述浅水中小振幅长波的单向运动,是一类分布参数系统,即
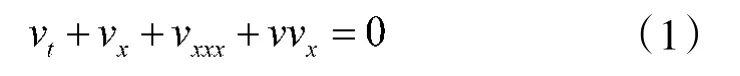
其中,v(t,x)是水波的高度。在现实情形,耗散效应和非线性色散效应对物理系统的影响同样很重要。文献[12]研究了一类具阻尼的广义KdV 方程。
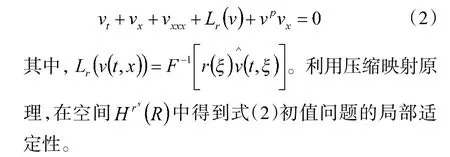
考虑到耗散效应的影响,本文研究一类具阻尼广义KdV 方程的控制问题。

本文拟采用P 型学习律设计出迭代学习控制器,给出此分布参数系统迭代学习控制算法收敛的充分条件及数值实例。
1 预备知识


2 局部适定性
本节给出式(3)的局部适定性定理及证明。

证明 主要利用引理1~引理4 及文献[12]给出定理1 的证明。利用半群理论,对于式(3),有


3 迭代学习收敛性分析

对于式(3),采用P 型迭代学习控制算法
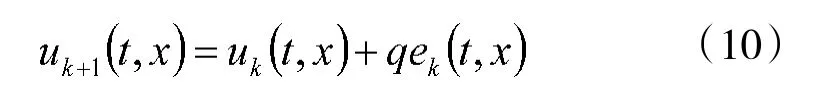
其中,k 表示迭代次数,q>0 是待寻的学习增益。假设在迭代过程中系统的初始状态允许存在一定的误差,即

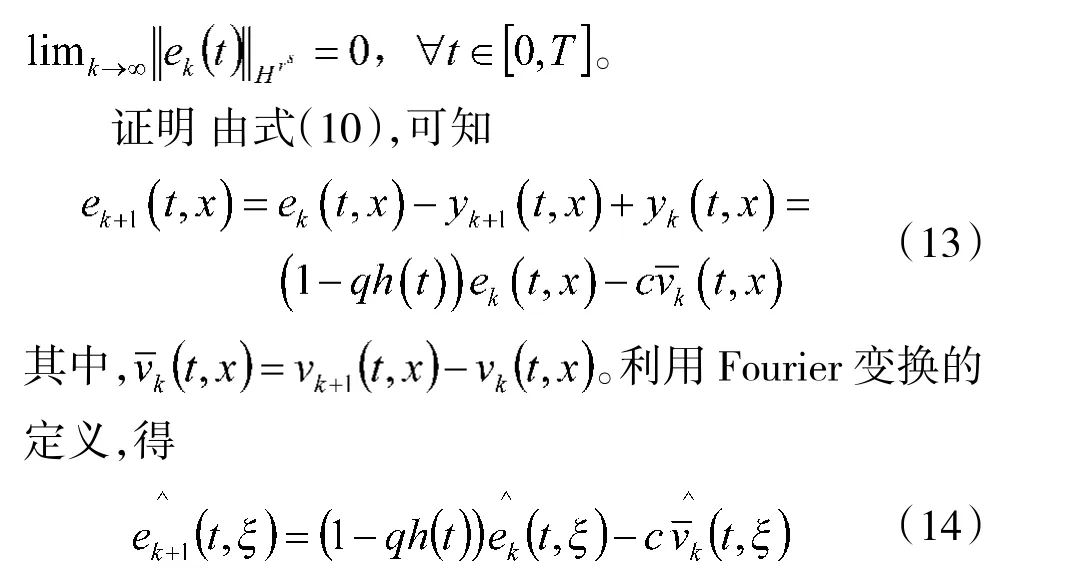
利用半群理论及式(3),得
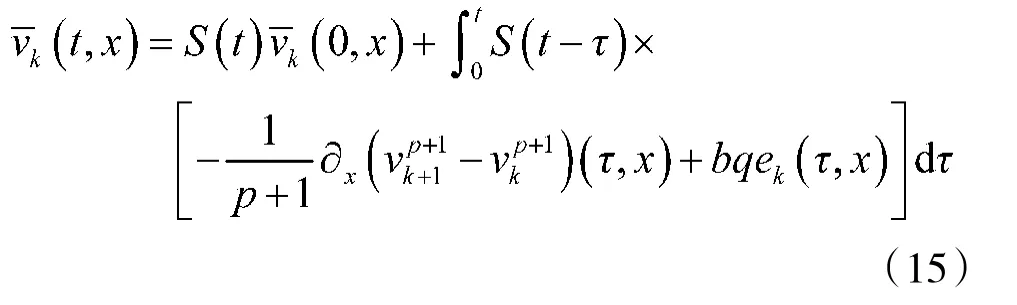
因此
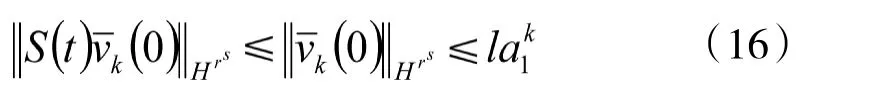
利用引理4,得到
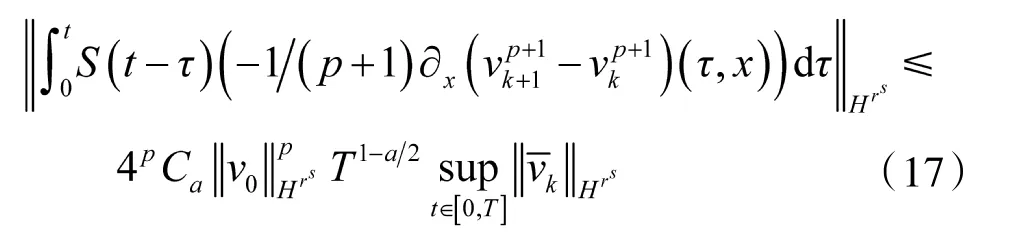
及
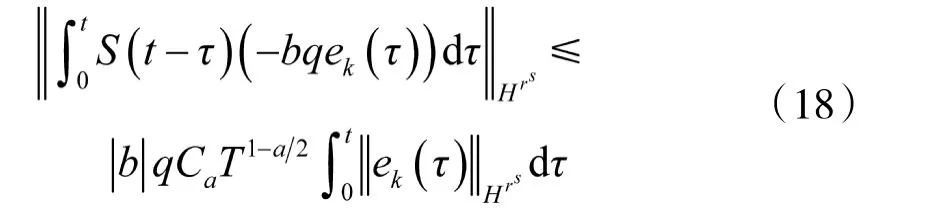
由式(15)和式(16),可知



4 数值实例

从而说明可选取适当的h(t)与ε,进而得到相对应的学习增益q。
5 结论

