基于信息扩散估计的水陆水准测量数据融合处理方法

张 浩,赵仲荣,梅 红,孙钰斌,夏成洋

(1.河海大学地球科学与工程学院,江苏 南京 211100;2.中交隧道工程局有限公司盾构分公司,北京 100000)

最小二乘估计以及抗差估计是最常用的2种参数估计方法。当观测数据服从正态分布时,最小二乘估计为最优的线性无偏估计,但最小二乘估计抗差性较差。对于抗差估计,当观测数据中不含粗差时,又会使估计结果不如最小二乘估计[1-3]。在大型跨江桥隧工程建设中,为了检验跨江两岸水准基准点的基准一致性及稳定性,必须进行相应等级的跨江水准测量,但目前GNSS测量尚不能完全替代高等级的水准测量,高程网常分两部分水准测量,陆地采用几何水准测量,跨江水准采用测距三角高程法[4-6]。虽然跨江测距三角高程测量采用多时段、多测回同时对向观测,但仍不能完全消除大气折光对观测高差的影响,随着跨江长度的增加,这种系统误差的影响更加显著,而观测过程和作业顺序严格依照规范执行,各项限差均满足规范相应等级要求,在水陆水准观测数据未知服从何种分布的情况下,为了使参数估计既不受粗差影响,又能得到最优无偏估计,应用信息扩散估计理论对水准路线各测段的往返较差值子集信息采用概率密度函数分布赋予权值,然后再进行最小二乘法进行联合平差,使得在不同环境条件下的水陆水准测量数据更好地融合。

1 信息扩散估计原理

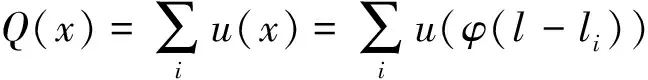
设μ(x)为定义在(-∞,+∞)上的一个波雷尔可测函数,d>0为常数,n为子样容量,则称

(1)

为母体Ω的概率密度函数f(l)的一个扩散估计,式(1)中:μ(x)称为扩散函数;d称为窗宽;n维向量l称为扩散向量。对于不同的μ(x),可得到不同的扩散估计f(l)。根据分子扩散理论导出的正态扩散函数为

(2)

(3)

式(3)中h=σd确定的h称为标准正态扩散的窗宽。根据择近原则导出的窗宽h的经验公式为

h=α(b-a)/(n-1),

(4)

其中:a=min(li),b=max(li),i=1,2,3,…,n;α是n的函数,当n≥17时,α=1.420 693 101。

根据式(3)可知,观测值l必须为同一类观测值,且在理想状态下,各观测值应有相同的数学期望[10-11]。而水陆水准混合网因涉及到两类观测值,不能直接用于信息扩散估计。根据水准测量的特点,在实际测量工作中,等级水准每测段往往需要往返观测,各测段的较差di可视为一维的同类观测向量,且数学期望E(di)=0,这样就满足式(3)的条件,即用di代替式(3)中各测段的观测值li。di在扩散估计f(d)中的概率f(di)越大,则li在分布f(l)中的概率f(li)也越大,于是就可以根据分布f(d)来赋予观测值li的权值。这样,各观测值的权值不是简单的距离关系,而是概率密度函数f(d)信息扩散估计的分布关系,可以将水陆水准测量数据更好地融合进行联合平差计算。

2 水陆水准数据融合处理的应用

图1 长江隧道高程控制网示意图Fig.1 Diagram of cross-river tunnel height control network

在此不妨以每千米往返高差中数为单位权(Pi= 1/Si)及第一测段往返较差d1分布值为单位权(pi=f(di)/f(d1))分别赋予各测段2种方法的权值比,其结果见表1。

由表1可知,依距离定权显著地反映了各测段误差随距离的增长而积累的特点,相同距离的跨江边与陆地边观测值赋予的权比为1∶1;而f(d)分布直接依据观测值的质量优劣赋予权值,相同距离的跨江边与陆地边观测值赋予的权比为1∶7,由于陆地几何水准测量受测站视距等限差的控制,受到折光等系统误差的影响较小,而跨江测距三角高程受折光的影响较大,权值比客观地反映了陆地水准的作业环境和观测条件优于跨江测距三角高程测量,同时陆地几何水准测量测段观测值的权值不与距离成比例关系,f(d)分布反映了陆地水准各测段间的偶然误差可以相互抵消的特征。

将表1中的水陆水准数据按2种方法赋权进行联合平差,求得的高程平差值Hi、点位误差σi、高程平差值差异值(绝对值)结果见表2,单位权中误差σ0结果见表3,其各高程点的误差分布如图2所示。

由表2及图2可知,水陆水准采用经验定权与分布赋权联合平差结果:高程网的高程精度分布趋于一致,离已知点近的区域高程点位精度较高,高程网中间区域的点位精度相对较低,但分布赋权的精度整体高于经验定权精度,点位精度比经验定权法在最弱点处提高约1.27 mm,而且分布赋权的高程点精度更加均匀。由表3可知,采用分布赋权相对于经验定权法,使整个网型的验后单位权中误差提高 0.51 mm,分布赋权的单位权中误差更趋近于陆地二等水准偶然中误差的估算精度,表明高程网分布赋权的抗差性更优。

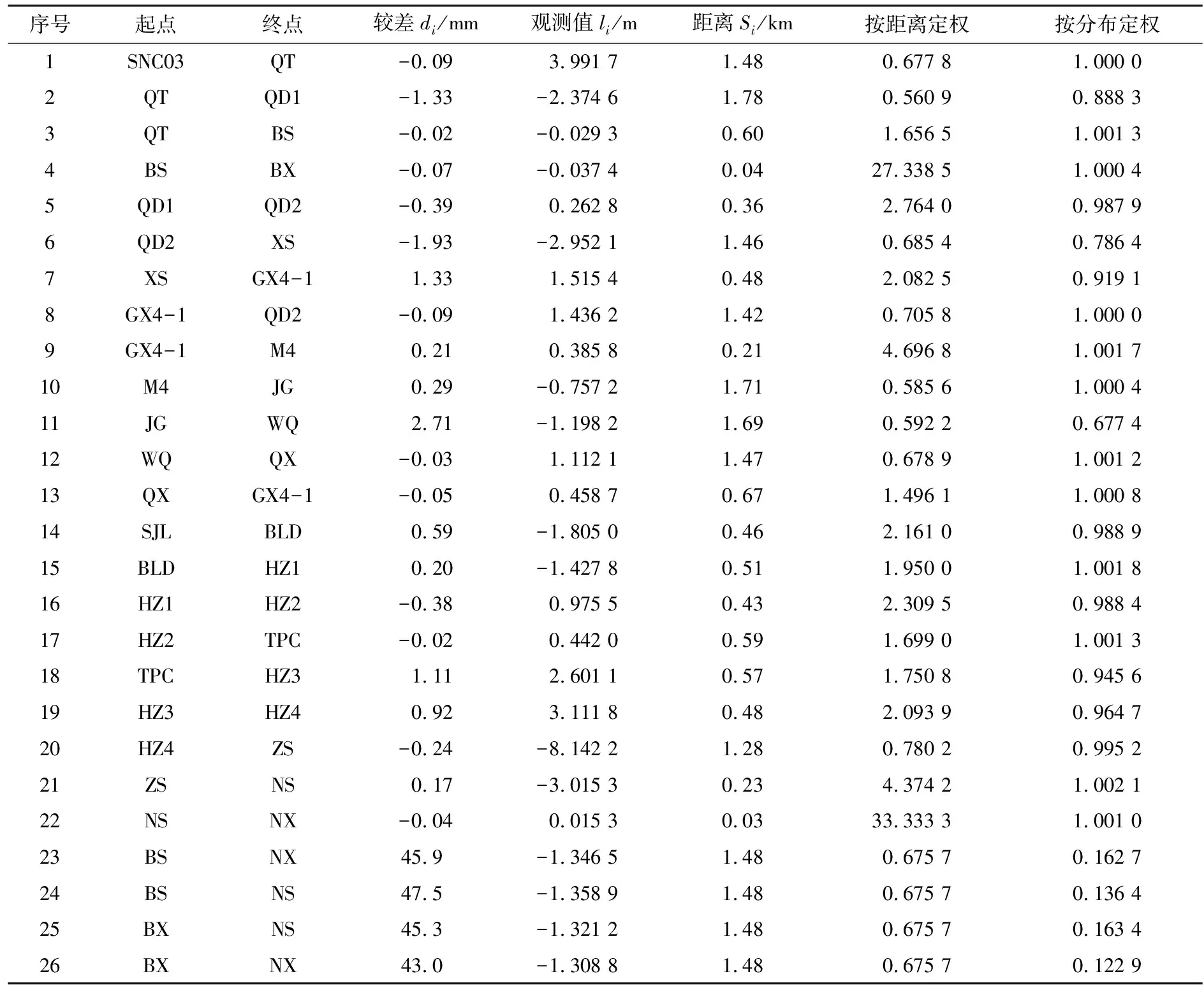
表1 陆地水准与跨江水准观测值及较差

表2 水陆高程网平差结果

表3 水陆高程网单位权中误差

图2 水陆高程网控制点误差分布Fig.2 Error distribution of land-water height control points

3 结论

在大型跨江盾构隧道施工中,隧道高程数据缺少必要的检核条件,其贯通精度完全取决于地面水准和跨江水准的观测精度及数据融合处理方法。对观测数据各项限差均满足规范相应等级要求,但在未知服从何种分布的情况下,建立水陆水准参数概率密度分布函数的信息扩散估计,充分利用样本提供的数据信息,根据信息扩散原理来推断参数的概率密度分布,依据各观测值的观测质量赋予权值,将水陆水准数据更好地融合,联合平差计算结果比经验定权法更具有抗差效果,使高程网的整体精度得到了提高,单位权中误差更切合规范相应的等级。