配电网状态估计可观性研究综述

2022-04-26韩平平吴红斌

电力系统及其自动化学报 2022年4期

韩平平，张楠，潘薇，吴红斌

（安徽省新能源利用与节能省级实验室（合肥工业大学），合肥 230009）

随着社会经济和可再生能源利用技术的迅速发展，越来越多的分布式电源与电动汽车规模化接入配电网，改变了传统配电网单向潮流的基本格局，加剧了网架结构的复杂性，且电网运行状态还将因分布式电源出力的随机性而频繁变化。配电网作为电力系统的终端，直接与用户相连，其运行状态直接关系到供电的可靠性。因此，及时准确地获取配电网的实时状态至关重要[1]。

状态估计是实时感知和精细管控系统运行状态的关键手段[2]。在运行系统中，状态估计软件由拓扑处理、可观性分析、状态估计和坏数据处理等模块组成[3]。其中，可观性分析是状态估计的前提，是判断已知量测数据是否能唯一确定系统状态的过程。输电网可观性研究方法已较为成熟，对配电网可观性研究起到了很好的借鉴作用。但是，相较于输电网，配电网具有更大的节点规模、更多变的拓扑结构和严重的三相负荷不平衡问题等特点，使得适用于输电网的可观性分析方法和可观度提高方案不能直接应用于配电网。由此可见，研究适用于配电网的分析方法和提高方案具有重要意义。此外，分布式电源与电动汽车的接入为配电网状态估计可观性带来了新的挑战。

综上，本文依次对配电网可观性分析方法、配电网可观度提高手段、主动配电网伪量测建模技术的研究现状和成果进行梳理和综述，为解决实际系统存在的不可观问题及后续研究提供借鉴与参考。

1 配电网状态估计可观性分析技术

1.1 状态估计原理

电力系统中，在给定拓扑结构、线路参数和量测集合的条件下，状态估计量测方程可表示为

式中：z为量测量矢量；h(x)为非线性量测函数矢量；x为状态矢量；v为量测误差。

状态估计是根据量测系统冗余度和估计准则确定系统最可信状态量的过程，提高了数据精准度与数据系统的完整性。在估计准则中，加权最小二乘准则应用最广泛，其数学模型为

式中：J(x)为目标函数；R-1为量测权重。

可观性分析是指分析能否通过已知网络和量测集合进行状态估计，确定系统的当前状态。若通过可观性分析判定量测正定或超定，利用已知量测可以完成状态估计，则系统可观；若通过可观性分析判定量测欠定，状态估计因缺乏必要量测而无法执行，则系统不可观。系统的可观度可以通过优化量测配置、伪量测建模或增加额外测量装置等手段来提高。具体体现为：①生成满秩的雅可比矩阵或满秩树，使得系统由不可观变为可观；②减小可观系统中的不可观风险指标值，使得系统的不可观风险降低；③增加了可观系统的可用量测，使得可观度进一步提升，同时状态估计计算结果的精度也得到提高。

1.2 配电网可观性分析方法

目前配电网可观性分析方法主要为数值法和拓扑法。数值法是通过信息矩阵能否完成因子分解且对角线不出现零主元或雅可比矩阵是否列满秩来判断网络是否可观，说明只有当线性无关的测量值数目大于或等于状态变量数目时才满足可观条件。信息矩阵为

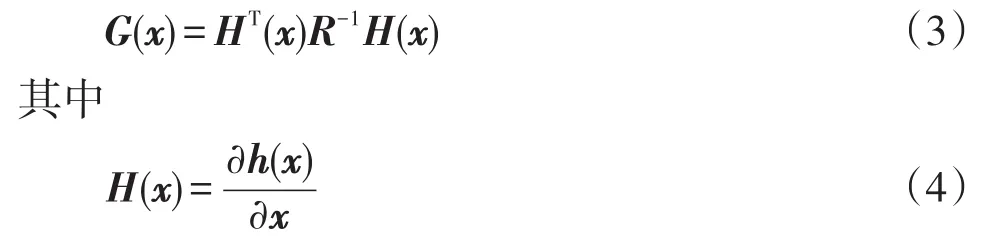
式中：G(x)为信息矩阵；H(x)为雅可比矩阵。

该方法具有避免迭代计算和无需额外编程的优点，在小型电力系统中应用较多。在输电网中，相关文献多从雅可比矩阵或信息矩阵的三角分解[4]、雅可比矩阵的零空间[5]、雅可比矩阵的Gram矩阵[6]等角度研究网络可观性，然而所采用的线性化解耦和单相建模的分析理论不能完全适用于阻抗比值大、三相耦合且不平衡情况较为严重的配电网中。基于此，文献[7]提出基于正交线性变换的数值可观性分析方法来解决配电网中阻抗比值大的问题。文献[8]基于量测雅可比矩阵中P与V、Q、θ弱耦合，提出一种多相数值可观性分析方法，为多相不平衡配电网的可观性分析提供了思路。文献[9]考虑了配电网中伪量测的位置和数量，对量测数据的优先级进行排序，并通过信息矩阵的三角分解进行可观性判定，大大提高了分析效率。

拓扑法引入了图论的思想，若能根据量测信息的搜索建立1个包含整个网络所有节点的满秩树，则网络可观，否则网络不可观，此时可通过在较小树之间添加可观测分支来满足可观性。该方法避免了数值法中的浮点运算，分析速度快，广泛应用于电力系统中。常用算法是先利用深度优先搜索法对有潮流量测的支路进行遍历搜索形成多个可观测区域，然后通过母线注入量测连通或扩大可观测区域，形成可观测岛。可将电力系统看作仅由顶点和边构成的图R=(V,E)，V表示顶点集合，E表示边集合，分别对应系统母线与支路的集合。可观测岛可看作1个测量子图R′=(V′,E′)，若V⊆V′，即子图R′包含了图R中所有顶点，则可证明系统拓扑可观。

现有拓扑可观性分析方法相关研究多集中于最大可观测岛的生成和可观性判定条件的选择[10-12]。针对配电网相量测量单元较少的现状，文献[13]提出基于潮流定解条件的配电网可观性拓扑分析方法，利用极少相角量测即可判断系统是否可观，文中所提方法也很好地适应了配电网辐射状的结构特点。

但由于传统的拓扑算法比较复杂，可能会出现组合爆炸问题。为解决此问题，有学者提出了一种拓扑-数值混合的可观性分析方法。例如，文献[14]首先利用拓扑法生成局部可观测区域，然后添加最小数量的伪量测潮流分支，最后通过基于解耦直流模型的数值可观性分析方法得到可观性分析结果，该混合分析方法是由复杂环网运行特点和图论中环的概念衍生，广泛用于大规模环形输电网，配电网中使用较少。

以上可观性分析方法均是基于已有量测的数量、类型和位置来确定可观性。然而部分配电系统中由于量测配置不足，还存在较多大误差伪量测，即使通过分析方法确定网络可观，状态估计结果也与网络真实状态存在较大差异，其表征该系统具有不合理的可观性。通过概率分析方法可以解决伪量测带来的不确定问题。例如，文献[15]在高斯分布的假设下，首先通过计算信息矩阵的方式得到了相应的概率密度函数PDF（probability density function），计算公式为

式中：αi为状态变量可能的取值；Ei为状态变量的估计值；为状态变量的方差，由信息矩阵逆矩阵的对角线元素表示。

然后用概率密度函数对状态变量置信区间进行计算，即

式中：αi_max、αi_min分别为置信区间上限、下限；CL为预先定义的置信度。

最后通过判断各节点参数的置信区间与其所要求估计精度的关系来判断网络的可观性。

配电网可观性分析可以追溯配电网不可观原因，从而为量测配置和伪量测添加提供针对性建议。总体而言，配电网的可观性分析方法尚处于初步研究阶段，如何将较为成熟的输电网分析方法用于配电网将是未来的研究热点。例如，随着环网解耦研究的逐步深入，为拓扑-数值法应用于配电网提供了可能。相量测量单元在配电网中规模化接入也为拓扑法的应用创造了条件。

1.3 配电网可观性评价指标

若确认系统可观，则需要建立1个综合的评价指标来表示不同量测集的可观度。该指标依赖于数据冗余，数据冗余不仅与量测数量有关，还取决于量测类型和位置。传统的定性可观性分析难以准确表达出此指标的特性。基于此，有学者提出不可观风险数值指标的概念，并对可观性的评价指标进行量化，直观地展现出不同量测系统的不可观程度[16]。将量化指标扩展到三相，可得到配电网可观性评价指标。

（1）不可观风险指标A1为失去任意1个量测后导致网络不可观的概率，计算公式为

式中：m为三相总量测数；NCmeans为三相关键量测总数。在所有量测中，若某一关键量测丢失，则会导致系统不可观。

（2）不可观风险指标A2为失去任意2个量测后导致网络不可观的概率，可引入文献[16]中关键量测组的概念，计算公式为

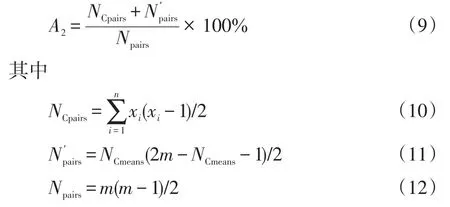
式中：NCpairs为关键量测组中任意失去2个量测的组合数；n为关键量测组的组数；xi为第i个关键量测组中的量测数；Np′airs为任意失去的两个量测中至少含有1个关键量测的组合数；Npairs为任意失去2个量测量的组合数。关键量测组由部分量测量组成，在关键量测组中丢失任意2个量测会导致系统不可观，丢失任意1个量测则不会导致系统不可观。可见，关键量测组与关键量测相互独立。

（3）不可观风险指标A3为任意1个量测配置不可用（其所提供测量数据均丢失）后导致网络不可观的概率，计算公式为

式中：Nrtus为量测配置总数；NCrtus为关键量测配置数。若某一关键量测完全不可用，则会导致系统不可观。

上述3种不可观风险指标可以量化系统不可观风险，数值越大风险越高[17]。不可观风险指标计算的难点在于关键量测量和关键量测组的辨识。与输电网相比，配电网节点和支路众多，网络规模庞大，三相数据均需进行分析，导致量测量剧增，大幅度提高了关键量测的辨识难度。配电网现有的关键量测辨识方法还难以满足指标计算精度的要求。因此，如何准确辨识配电网关键量测量和关键量测组仍需进一步研究。

2 配电网可观度提高技术

2.1 配电网量测技术概述

量测是状态估计的重要数据来源，其数据的质量和冗余情况直接影响了系统状态估计的可观性与准确性。配电系统中，常见量测技术包括数据采集与监视控制系统SCADA（supervisory control and data acquisition）和高级量测系统AMI（advanced metering infrastructure），统称为传统量测技术。其中，SCADA应用更为广泛，且成熟度较高，主要通过馈线终端单元FTU（feeder terminal unit）获得网络中支路功率、支路电流幅值和节点电压幅值等数据。AMI量测相比于SCADA量测，还可采集配电网末端节点的注入功率量测。

目前，以同步相量测量单元PMU（phasor measurement unit）为代表的新型量测技术也逐渐用于配电网。相比传统量测，PMU还可采集所在节点的电压相量和所连支路的电流相量，同时具有高采样率和能够给数据提供精确时标的特性[18-19]。现有配电网常见量测体系如图1所示。

图1 配电网常见量测体系Fig.1 Common measurement system of distribution network

随着量测技术的发展，不仅使得可应用于状态估计的数据量大为增加，同时也提高了数据的精确度，对配电网可观度的提高起到了积极的推动作用[20]。但由于PMU量测装置的成本较高，因此在未来较长时间内，配电网仍会保持PMU量测与传统量测并存的局面。PMU可解决传统量测的数据精度低和更新速度慢等困难，但其自身数据与传统量测数据同步性较差，加大了时间坐标对齐的难度。因此，如何充分挖掘两种量测系统的数据特点，研究精度较高的多源数据融合方法，对于提高配电网状态估计可观度具有重要意义。

2.2 量测配置的优化技术

随着配电网智能化研究的逐步深入，数据种类与数量需求增多，对量测配置的要求也日益严格。在配电网中，量测配置过少会导致不可观问题，状态估计无法正常进行。量测配置过多又不符合配电网节点众多、结构复杂的现状。因此，优化量测配置、辨识网络重要量测点对配电网状态估计可观度的提高具有重要作用。

2.2.1 满足系统可观度要求的优化配置模型

配电网量测配置优化评价指标以可观性、估计结果精确度、数值稳定性、经济性和可靠性等为主[21-23]。现有文献多是基于多个评价指标展开优化，其中实现可观性是必要条件。

研究发现，支路功率量测相较于其他量测对于配电网可观度提高贡献更大。因此，在传统量测优化配置模型中，支路功率可观理论获得较多应用。该理论表明，若根节点U1已知，各支路的功率可测得，则其余各节点电压可通过U1推导出，网络完全可观。现有FTU中“三遥”终端大多数可实现所在节点所有邻接支路功率的量测。基于此，可建立基于支路功率可观理论的配电终端优化模型[24]为

式中：yi表示节点i处是否安装配电终端，yi={0 ,1}，y1=1，yi=0表示不安装，yi=1表示安装；An×b为节点支路关联矩阵，An×b=[aij]n×b，n为节点数，b为支路数，若节点i与支路j相连，aij=1，否则aij=0；B1×b为支路可观判定矩阵，B1×b=[b1j]1×b，若第j条支路两端节点均为零注入节点，则b1j=0，否则b1j=1。

由第2.1节可知，传统量测还可获得节点电压幅值、支路电流幅值和节点功率等量测数据。其中，由于现有配电网中AMI量测尚未普及，多数节点功率量测仍旧由误差较大的伪量测代替。考虑到此类量测，在优化配置模型中可引入最大状态量偏差的概念，若利用已有量测（包括实时量测和伪量测），通过状态估计得到状态变量的估计误差均小于给定最大偏差，则系统可观，且估计误差越小，系统可观度越高[25]。基于此，可完成对配电终端的配置优化。另外，为展现不同量测量的重要程度，文献[26]利用广义逆矩阵和最小二乘法唯一最小解的数学方法确定误差表达式，对量测量重要性进行了排序，并结合经济性与可观度要求确定了最终的量测类型和安装位置。

根据PMU量测特点可知，传统量测的优化配置模型在PMU配置中同样适用。然而，PMU短期内难以实现在配电网中全面铺设[27]，且传统优化配置模型无法充分利用PMU提供的相量数据，为优化量测配置问题的研究带来新的挑战[28]。

在电力网络中，电压相量可量测或可求出的节点为可观节点，反之为不可观节点。PMU优化配置OPP（optimal PMU placement）的研究多是以各节点完全可观为约束条件。基于PMU量测的特性，常用的可观性分析规则[29]如下。

（1）若某节点配置PMU，则其相邻节点均可观。

（2）若某可观的零注入节点的相邻节点中仅有1个节点可观性未知，则该相邻节点是可观的。

（3）对于某可观性未知的零注入节点，若其相邻节点都可观，则该零注入节点可观；若相邻节点中存在不可观节点，则可利用节点方程来判断该零注入节点是否可观。

PMU最优配置的目标是保证满足系统的可观度和冗余度要求，确定PMU配置的最小数目np和最合适的位置S(np)。结合可观性分析规则，可将此类问题[30]表述为

式中：R[np,S(np)]为量测冗余度指数；O为节点可观性评估的逻辑函数。

考虑到PMU量测与传统量测并存的现状，可引入零注入节点和传统量测提供的支路功率与节点功率实时量测数据来满足式（15）约束条件的要求，并利用可观性分析规则（2）和规则（3）来提升网络可观度[31-32]。另外，有学者提出简化核心网可观性原则，只在网络枢纽部位装设PMU，若能提供重点联络线的电压及电流值，并能获得重点线路的状态轨迹变化情况和骨干网架的动态信息，即可认为该配置方式是合理的。

随着多源数据融合技术的成熟，将会有更复杂的量测数据参与到状态估计可观性的研究中，对量测优化配置模型提出更高的要求。因此，开发更易求解、更好适应多源数据融合结果的优化配置模型，对于提高状态估计可观度具有重要意义。

2.2.2 优化配置模型的求解方法

由上文可知，求解配电网量测配置优化问题的目标是找出系统最佳量测点与量测类型，并配置合理数量的量测单元。传统量测优化配置的求解过程与PMU类似，且PMU在配电网中已有较多的应用场景，因此本节只对OPP模型的求解方法展开论述。

OPP模型的求解方法主要分为确定性算法和启发式算法两大类。确定性算法以整数规划为代表，包括整数线性规划、整数二次规划、0-1规划法等，常用于解空间较小的场景，可以找到全局唯一最优解。启发式算法以智能搜索为基础，主要包括模拟退火法、禁忌搜索法、粒子群算法和遗传算法等，适用于求解高维度、非线性、多目标模型，全局搜索能力强，但易陷入局部最优，常用次优解替代全局最优解。各种算法的优缺点如表1所示。

表1 OPP算法优缺点Tab.1 Advantages and disadvantages of OPP algorithm

在解决实际问题中，常常将不同的算法配合使用，充分发挥各自的优势。例如，文献[33]基于遗传算法和模拟退火算法求解OPP问题，模拟退火算法用于降维搜索，遗传算法用于全局优化，提升搜索能力的同时提高了搜索效率。

近年来，基于上述方法，许多学者结合配电网特性对OPP求解问题进行了更深入的研究。文献[34]在充分考虑配电网辐射状拓扑的基础上，提出了等效缩小网络规模的方法，并对各网络分别进行OPP，满足了系统可观度要求并提高了优化速度。文献[35]给出了一种基于负载特性的配电网络压缩方法，并结合自适应遗传算法和禁忌搜索算法，使得PMU数量和系统冗余度同时达到最佳。文献[32]考虑了配电网拓扑的多变性，提出一种定制遗传算法，通过定制的交叉和变异，实现了多种拓扑结构平均可观节点数目的最大化。也有文献考虑到配电网中伪量测的存在，利用蒙特卡罗模拟方法配置PMU[36]。

OPP求解方法还有基于网络拓扑结构的算法，主要包括最小生成树和深度优先搜索法，计算速度快，可以更直观地展现PMU配置过程，有助于对电网结构进行深入分析。例如，文献[37]利用一种改进的图论方法形成了包含网络所有节点的最优生成树，然后选择PMU的关键安装位置，实现网络的完全可观。文献[38]提出一种基于图论和层次分析法的多准则决策方法，该方法利用图论的概念形成决策矩阵，应用层次分析法对优先级顶点进行排序，并考虑到零注入节点在OPP中的作用，满足了在单PMU缺失或线路中断情况下的网络仍然可观。但此类方法还存在着PMU配置数目较多，且配置方案单一的缺陷。

现有OPP求解方法大多用于解决可观度和冗余度的优化问题，在处理可靠性、状态估计精度等目标上效果不佳。因此在优化量测配置过程中，开发基于多目标函数的OPP求解方法仍是当前研究的重点内容。

2.3 伪量测建模与零注入节点处理

基于配电系统发展现状，并考虑到部分地区经济压力与量测体系建设难度较大，一些配电网络即使通过优化量测配置也难以满足状态估计可观度要求。此时通过增加伪量测和虚拟零注入量测的方法可以实现在不增加量测设施情况下的可观度的提高。常见的伪量测建模与零注入节点处理方法如图2所示。

图2 伪量测建模与零注入节点处理方法Fig.2 Method of pseudo-measurement modeling and zero injection node processing

2.3.1 伪量测建模方法

伪量测是指通过对历史数据、实时量测数据、天气情况等多方面因素的分析得到的未安装量测设施区域的运行数据。与实时量测相比，伪量测具有较大的误差，其误差大小直接影响状态估计可观度，进而影响估计结果的精度，因此研究高精度伪量测建模方法具有重要意义。

现有配电网状态估计伪量测多由短期负荷预测获得。短期负荷预测方法主要分为传统预测法和人工智能预测法[39]。传统预测法是利用统计学知识，对历史数据进行分析得到负荷伪量测，常见的方法有时间序列法、趋势外推法、卡尔曼滤波法等。该类方法曾在很长一段时间可以满足状态估计伪量测精度的需求，但是随着配电网规模的不断扩大和用户的持续扩增，简单的基于统计学的分析方法已难以处理更加复杂的非线性负荷。基于人工智能算法的负荷预测为这些问题提供了很好的解决方法。遗传算法、小波分析预测法、模糊控制法、神经网络等已广泛应用在基于短期负荷预测的伪量测建模中。例如，文献[40]通过深度信念网络DBN（deep belief network）算法进行配电网负荷预测，将多类型负荷的历史数据及其对应日期类别、温度作为训练数据，选择与当前负荷关联性较强的数据作为DBN输入，得到较高精度的伪量测。

上述方法均建立在历史样本数据之上，因而实时跟踪电力系统状态变化的能力较差。研究表明，基于历史负荷曲线对当前时刻量测值进行曲线拟合获取系统非线性函数的方法，可得到更加精确的未知节点负荷伪量测，同时可实时跟踪系统变化。例如，文献[41]将典型负荷曲线和从潮流模拟中得到的负荷数据用来训练人工神经网络ANN（artificial neural network），再将实际量测作为ANN的输入，获得了较高精度的节点注入功率伪量测。该方法将横向实时量测数据与纵向历史数据进行有效结合，并利用了ANN可以模拟人脑结构进行非线性映射的特点，使配电网状态估计的计算精度达到较高水平，但是ANN的预测性能会随着神经网络层数的增加而降低。于是具有更强计算与适应能力的脉冲神经网络被用于配电网伪量测建模[42]。

配电网中除功率数据外，其他类型数据同样存在缺失情况。这些数据对于满足可观度要求、提高状态估计精度同样具有重要作用。对此，文献[43]提出利用多元回归的数学方法对配电网节点电压数据进行建模，所得结果作为量测信息加入状态估计器中，并利用算例验证了所提建模方法的有效性，但该方法得到的电压伪量测数据精度较低。因此，剖析配电网中负荷历史数据与电压、电流等非负荷历史数据的关联机理，探寻更适合于非负荷伪量测建模的方法将是状态估计一个有意义的研究方向。

2.3.2 零注入节点处理方法

除了伪量测，实际配电网中还存在大量零注入节点。该类节点注入功率为0，不需要通过量测装置获取。若能将这些零注入节点功率作为量测量进行状态估计，则可以大幅提高系统冗余度，满足状态估计可观度要求。但是，在配电网状态估计中，零注入节点功率的输出结果有时难以保证严格为0，导致这些节点无法满足潮流方程。因此，如何保证零注入节点输出功率严格为0是计及零注入节点状态估计研究中的重要问题。

在处理零注入节点时，一般采用加大权重法和拉格朗日乘子法两种方法[44]。加大权重法是将零注入节点的注入功率视为精确度非常高的虚拟量测，给予其较大权重进行状态估计计算。这种方法简单方便、计算量小，但只能保证状态估计结果中零注入节点的功率近似为0，同时还可能引起信息矩阵病态。在配电网中，R/X比值较大，引起信息矩阵病态的情况更为严重。拉格朗日乘子法是将零注入节点注入功率为0作为状态估计目标函数的约束条件。该方法可以实现零注入约束的功率输出严格为0，但该方法的信息矩阵不再正定，还需计算乘子协方差矩阵的对角元素，导致计算效率较低[45]。基于拉格朗日乘子法的缺点，文献[40]受到基于修正牛顿法的零注入节点处理方法的启发，将零注入约束转化为线性约束，在一定程度上提升了计算效率[46-47]。

上文提到的零注入节点处理方法与现有配电网状态估计算法还存在兼容性较差的缺陷，无法同时满足计算速度与计算精度的要求。因此，如何使零注入节点处理方法更好地适应状态估计算法仍是提高状态估计可观度与结果准确性的关键。

此外，随着可再生能源发电技术的发展，多类型分布式电源DG（distributed generation）和电动汽车等设备规模化接入配电网，使得传统配电网逐渐向具有控制能力的主动配电网发展。在主动配电网中，伪量测建模方法也将有所差异，主要体现在两个方面：①DG并网机理与传统电源有很大不同，若想实现全网可观，则有必要基于并网机理对DG出力伪量测进行合理建模；②主动配电网功率不再是单向流动，电源和负荷拥有双重不确定性，用户具备生产者和消费者双重身份，对伪量测建模具有较大影响[48]。因此需专门针对主动配电网的伪量测建模方法进行探讨。

3 适用于主动配电网的伪量测建模技术

3.1 基于分布式电源并网机理的伪量测建模方法

主动配电网中传统的负荷建模方法与第2.3.1节类似。对于主动配电网中DG的伪量测建模，一般将其作为有功功率-无功功率注入节点[49]。首先对DG的三相总出力进行预测，假设三相注入功率相等，进而得到单相功率注入伪量测，提高系统可观度[50-51]。但该方法未考虑DG的不同并网机理，且未计及DG出力与配电网的三相不对称性，导致伪量测精度较低。基于此，文献[52]根据不同类型DG出力的特性，将DG并网节点类型分为有功及无功恒定的PQ节点、有功及电压恒定的PV节点、有功及电流恒定的PI节点、有功恒定及无功受电压限制的PQ（V）节点。通过对上述恒定物理量进行建模来可以提高含不同类型DG系统的伪量测精度。

另外，基于并网机理不同还可将DG分为直接并网（包括同步、异步风力发电机）和经脉宽调制PWM（pulse width modulation）换流器并网（包括光伏发电系统等）两种类型。这两种模型的等效电路分别如图3和图4所示。

图3 DG直接并网Fig.3 DG directly connected to grid

图4 DG经PWM换流器并网Fig.4 DG connected to grid through PWM converter

这两种并网模型中，直接并网风电机组与PWM换流器的端口电压均呈三相对称性，能够用单相相量表示其三相电压，在状态估计过程中可将状态变量扩展为

式中：˙为网侧三相节点电压状态变量；E0和δ0分别为风电机组（或PWM换流器）端口的电压幅值和相角。由此可见，基于并网机理的DG伪量测建模可更好适应配电网三相不对称的特点。

在上述基础上，文献[53]提出在直接并网模型中，利用DG出力与功率因数得到的总有功功率与总无功功率可直接作为伪量测参与到状态估计中。在经PWM换流器并网的模型中，根据控制策略的不同将伪量测模型分为

今后，将会有更多的DG并网方式出现，电力电子设备的应用类型也逐渐增多，DG可能会像同步机一样参与电网调频调压，使得DG的伪量测建模更加困难，将会给状态估计带来更大的挑战。因此，基于并网机理的分布式电源伪量测建模在配电网状态估计可观性研究中还有很大的潜力。

3.2 基于分布式电源与电动汽车不确定性的伪量测建模方法

在充分考虑主动配电网中分布式电源与电动汽车不确定性的情况下，现有伪量测精度提高方法主要有概率分布法[54-55]、模糊理论法[56]和区间数法[57]。概率分布法是根据大量历史数据获取分布式电源与负荷的概率分布，得到不确定变量的详细先验概率密度函数，进而获得变量较为精确的伪量测值。文献[54]在此基础上利用高斯混合模型对DG出力伪量测概率密度函数进行表述，并用该函数方差替换最小二乘法状态估计中原有的量测权重矩阵，取得了较好的估计效果。模糊理论法是通过建立不确定变量的隶属度函数来表达相应伪量测。文献[56]采用三角形隶属度函数表示不确定测量值和参数的模糊数，提高了系统的可观度，并得到了精度较高的状态量估计值。

但由于DG出力与电动汽车充电过程的完整概率分布获取难度较大，限制了以上两种方法在主动配电网中的应用。相比于概率分布法与模糊理论法，利用区间数方法来获得主动配电网中不确定变量伪量测问题无需建立参数具体的概率分布，只需知道其功率波动的上下界限即可，并且状态估计结果可以提供更直观的状态变量上下界信息，故这种方法在主动配电网伪量测建模中的应用潜力巨大。文献[58]建立了区间数的DG出力伪量测模型。对于风力发电，基于在线序贯-极限学习机的风电功率预测方法[59]，将输出模式由单输出转化为双输出，进而得到风机出力伪量测的区间值。对于光伏发电，考虑到其出力区间受多因素影响，利用区间覆盖率和区间宽度的综合评估将多目标优化转化为单目标优化[60]。所建立区间综合评定函数为

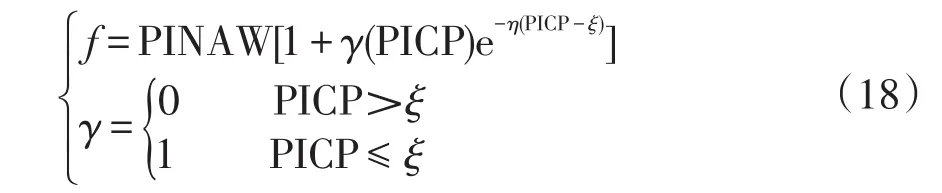
式中：PINAW为区间宽度；PICP为区间覆盖率；γ为判定参量；ξ为置信度，也是f的调节参数；η为f的调节参数，一般取η∈[50,100]。将该优化函数代入到粒子群算法中可得到光伏出力伪量测的最优区间。

电动汽车充电过程具有强不确定性，难以从机理方向对其进行伪量测建模。因此，在利用区间数法对电动汽车不确定分析之前，应先通过一定数学方法找出历史数据规律。基于此，文献[57]采用基于统计数学的蒙特卡罗抽样法与区间数法相结合的方式，对电动汽车充电过程中的负荷需求进行伪量测建模，文中首先利用蒙特卡罗方法对电动汽车1 d中各时间断面总需求进行抽样，并计算其期望值和标准差，然后用区间数对充电需求伪量测进行表述，即

式中：μEV为抽样数据的期望值；σEV为抽样数据的标准差；PEV(+)、PEV(-)分别为充电需求伪量测的最大值和最小值；υ为区间数的半径调节参数，根据实际情况进行设定。随着技术的发展，电网中出现了越来越多的储能设备，电动汽车也可作为分布式电源向电网放电，加剧了主动配电网的不确定性。为满足系统可观度要求，对不确定性变量的伪量测建模方法提出了更高的要求。