卫星可折展空间碎片防护机构动力学分析
2022-04-26陈传志崔继云陈金宝霍伟航李家琪江安澜
陈传志,崔继云,陈金宝,霍伟航,李家琪,江安澜
(南京航空航天大学航天学院 深空星表探测机构技术重点实验室,江苏 南京 210016)
0 引言
随着航天技术的发展,外层空间利用已逐渐成为各国关注和发展的重点方向。近年来,空间碎片环境日益恶化,太空垃圾总质量综合预计超过了几千吨,总数量超过200亿,其中1~10 cm的空间碎片数量超过75万个[1]。空间碎片与航天器相对撞击速度高达15 km/s[2],毫米级尺寸的空间碎片即可对航天器关键部件造成严重损伤,航天器在遭受空间碎片撞击后,会导致舱壁性能改变、表面成坑、穿孔,甚至发生容器破裂、爆炸等严重事故[3],日趋恶化的空间碎片环境严重威胁航天器的在轨运行安全。
卫星作为一类重要的航天器,在通信、导航、侦查和气候监测等方面发挥着及其重要的作用。由于大多数卫星运行在中低轨道,而绝大部分空间碎片分布在低地球轨道(LEO),因此,卫星遭遇空间碎片撞击的风险非常高。但是,目前国内外针对空间碎片的航天器防护结构集中于载人飞船、空间站等大型航天器,而且受质量、体积和发射成本等因素限制,只对毫米级碎片撞击有效果且防护面积有限,防护区域仅限于航天器关键部位。而国内外对于卫星的空间碎片防护结构设计尚处于空白,我国的卫星基本上都是没有增设空间碎片防护结构的“裸星”[4]。因此,有必要设计一种可展开空间碎片防护机构,在卫星进入空间碎片运行的高风险区域时,防护机构展开以应对速度5 km/s的厘米级碎片的撞击,处于低风险区域时防护机构可折叠,通过可折叠、展开机构,最大程度地增加星体的防护面积。
开展研制具备主动防御机制的卫星柔性防御系统,可大大提升空间系统的可恢复性、经济性、安全性与生存能力,对提升对抗环境下空间装备的体系抗毁与任务持续保障能力具有重要意义。
本文通过D-H法建立可折展机构的运动学模型,研究各多层柔性防护层的运动规律,结合机构运动学仿真验证其正确性,对可折展机构展开运动的实时精准控制具有重要意义。在此基础上,运用Lagrange动力学方程,对关节铰链的驱动力矩进行了分析求解并对驱动运动形式进行优化。
1 可折展防护机构
可折展防护机构主要由驱动装置、传动机构、可折展机构、多层柔性防护层以及分离锁定装置等组成。可折展防护机构安装于卫星星体侧壁,防护对象为六面体结构形式的侦查卫星、遥感卫星或气象卫星,如高分系列卫星、风云系列卫星等。防护目标设定为5 km/s速度下的10 mm尺寸的弹丸,可折展防护机构具有重复展开的特性,为增强卫星调姿变轨的稳定性,设计有分离锁定装置。
按照功能需求,结合工作环境,对防护机构进行功能性分析,为了尽可能不影响卫星其他有效载荷的使用,可折展防护机构采用太阳翼构型设计方法对称安装于星体两侧[5],如图1所示。在面临碎片的撞击风险时,机构在电机驱动下展开,展开完成后2个机构通过电磁锁定装置进行锁定,当撞击风险解除,机构解锁、收拢,按照“展开—锁定—解锁—收拢”这一流程循环工作。
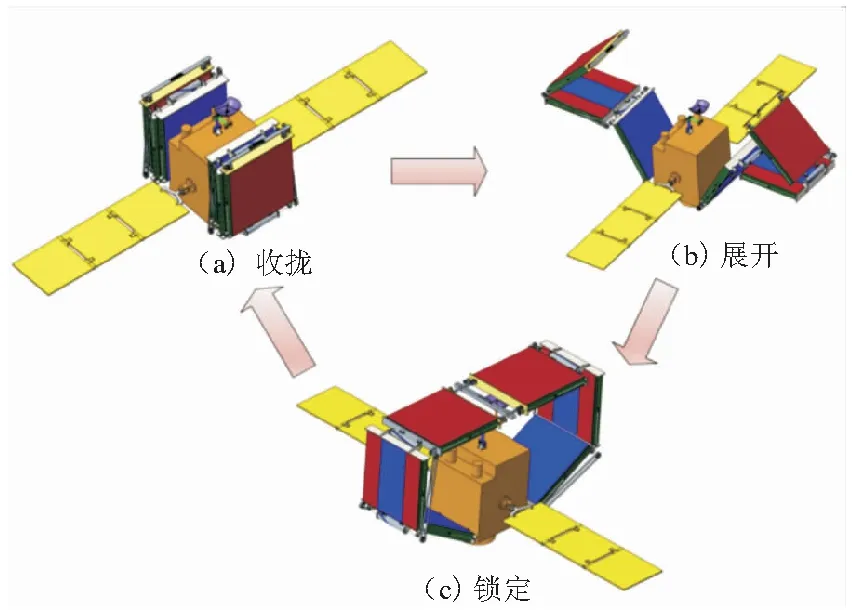
图1 可折展防护机构工作流程
如图2所示为可折展防护机构结构。防护机构主要由驱动装置、根部关节铰链、中部关节铰链、端部关节铰连、同步带传动装置、Kevlar-芳纶防护层、芳纶防护层、锁定装置和支撑杆等部分组成,机构的可折展功能由各关节铰链实现,各防护层用于防护空间碎片的撞击。
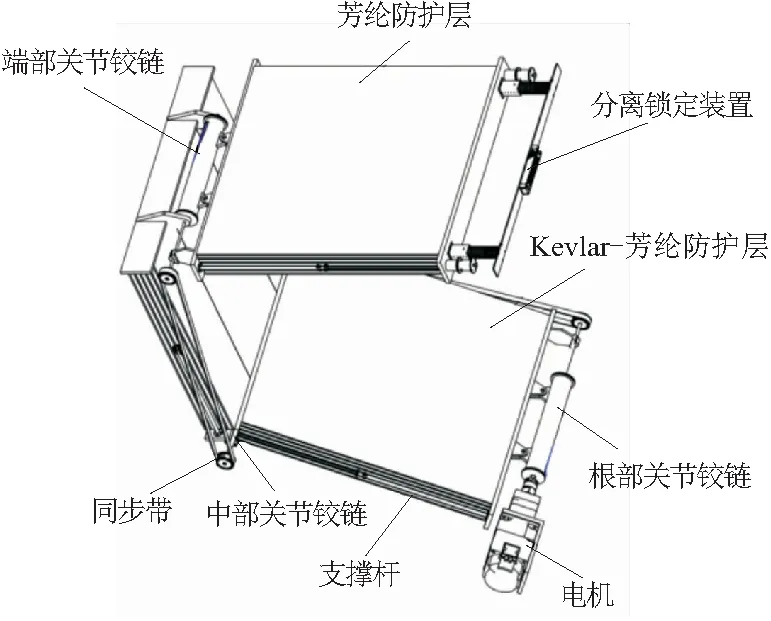
图2 可折展防护机构结构
1.1 可折展关节铰链结构设计
可折展关节铰链结构如图3所示。由圆柱凸轮、丝杠、丝杠螺母、凸轮滚子和同步带轮组成,其他关节铰链结构与之相同。电机动力经减速器输入至丝杠,驱动丝杠逆时针转动,丝杠带动同步带逆时针转动,经同步带轮带动中部关节铰链丝杠顺时针转动,凸轮滚子驱动凸轮转动。同理,经同步带轮传动,端部关节铰在丝杠、凸轮滚子的驱动下逆时针转动,凸轮采用正弦加速度推程运动规律,以避免凸轮旋转过程中速度、加速度突变产生的刚性和柔性冲击[6]。

图3 根部关节铰链结构
1.2 多层柔性防护层结构设计
多层柔性防护层的设计,依据的是未来空间站扩展舱体或大型空间居住舱的充气展开密封结构。扩展舱或居住舱外蒙皮的充气密封结构由热控层、辐射防护层、空间碎片和微流星体防护层、增强层以及气密层等组成,每层又由多种材料构成。其中,空间碎片和微流星体防护层主要用于抵御空间碎片的超高速撞击[7]。
如图4所示为多层柔性防护层的结构。Kevlar织物与芳纶织物交替排列,2种织物之间填充聚氨酯泡沫,Kevlar、芳纶织物厚度均为8 mm,聚氨酯泡沫厚度为20 mm,柔性防护层总厚度为148 mm。

图4 多层柔性防护层结构设计
2 可折展防护机构运动学分析
防护机构能否顺利可靠地展开,对卫星本体的防护至关重要,在对防护机构的各铰链运动学分析的基础上,为了进一步验证可折展防护机构展开合理性和稳定性,需要对机构进行运动学建模分析。结合关节铰链的运动特征求得各防护层相对于基坐标系的位移、速度、加速度的运动规律,以及电磁锁定装置的运动函数,通过理论计算与仿真相结合验证运动学建模的正确性和机构设计的合理性。
2.1 可折展防护机构运动学分析
可折展防护机构根据其机构特点,可简化为平面三自由度连杆机构,根据D-H法建立如图5所示的三自由度连杆机构的连杆坐标系[8]。
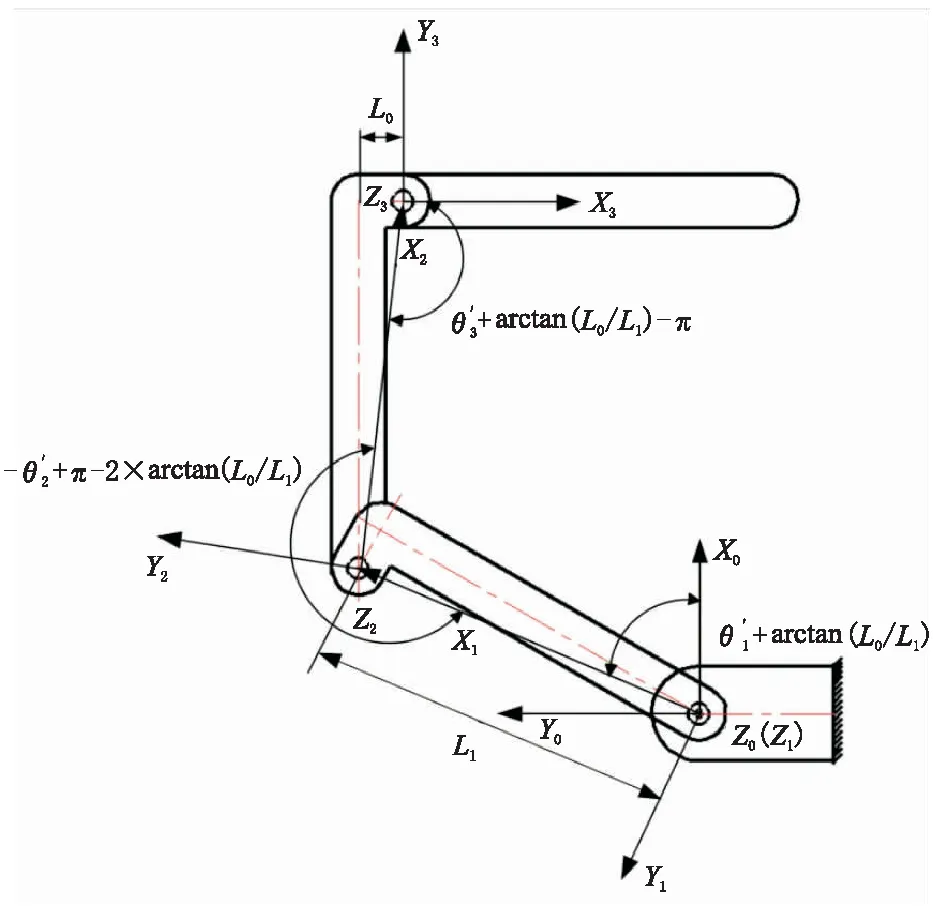
图5 机构运动简图
根据已建立的连杆坐标系,可获得其D-H参数,如表1所示。

表1 机构D-H参数

(1)
C1、S1分别为cosθ1、sinθ1;C12、S12分别为cos(θ1+θ2)、sin(θ1+θ2);C123、S123分别为cos(θ1+θ2+θ3)、sin(θ1+θ2+θ3)。
如图6所示为防护折展机构末端电磁锁轨迹曲线。初始位置末端在D-H系中的坐标为(1 902,-354.4,0),之后在一定的时间段内由于各关节铰的耦合运动横纵坐标逐渐增大,中部关节铰旋转速度比其他2个铰链的旋转速度更大,当末端的横纵轴坐标达到最大值后便逐渐减小,最后到达指定位置坐标(1 453,330)。仿真轨迹曲线与理论轨迹曲线趋势相同,由于模型存在误差且被放大,导致存在一定的误差。
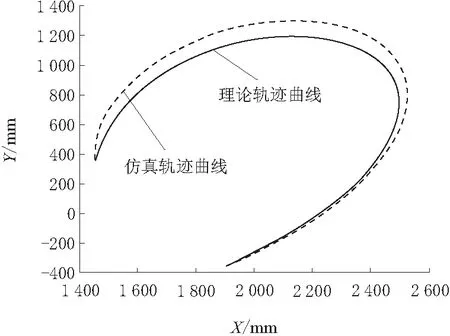
图6 末端轨迹曲线
2.2 可折展防护机构雅可比矩阵
为进一步研究关节铰旋转速度与防护折展机构末端速度关系,以及可折展防护机构各防护层的运动(转动与平动),需通过速度雅克比矩阵将其运动形式表示出来[9],求得末端相对于世界坐标系O0-X0Y0Z0的位置相量的速度雅克比矩阵,末端相对于固定端的运动学表达式为:
x=x(q)
(2)
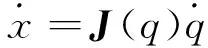
(3)
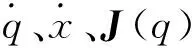
(4)
Jp1、Jp2、Jp3为操作空间和关节空间的线速度传动比;Jr1、Jr2、Jr3为角速度传动比。由于可折展防御装置的运动副都是转动副,可使用矢量积法求解雅克比矩阵,即
(5)
0Pi-1为末端质心相对于Oi-1-Xi-1Yi-1Zi-1的位置矢量。其在基座标系中的表达式为:
(6)
(7)
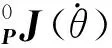
(8)
在机构运行过程中不同时间段内,末端速度的变化曲线如图7所示。0~4.4 s末端速度一直为0;4.4~15.6 s速度持续增加,在15.6 s时刻达到一个极大值98.4 mm/s;然后速度出现短暂的下降,在23.6 s时刻降至79.1 mm/s;之后速度再次增加,在35.1 s时刻达到最大值135.7 mm/s;最后速度持续降低直至为0。
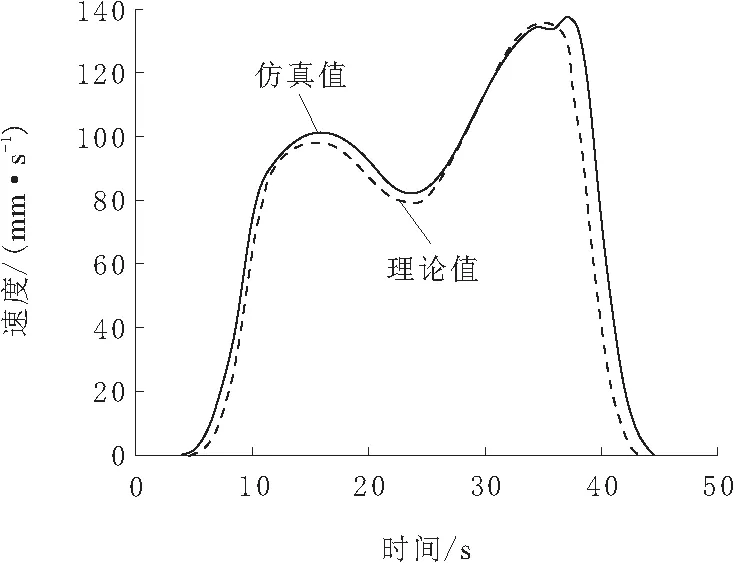
图7 末端速度-时间曲线
2.3 关节铰驱动力矩求解
为求解各个关节铰驱动力矩,通过Lagrange动力学方程建立关节铰与防护层运动参数的动力学模型,基于ADAMS建立其动力学仿真模型,通过理论计算和仿真相结合验证动力力学模型的正确性。
基于Lagrange动力学模型,结合可折展防御装置结构参数和物理参数,进一步得到可折展防御装置展开动力学参数。驱动装置丝杠螺母采用运动学分析中的余弦函数,展开时间t=48.4 s,各个关节铰的角速度、角加速度采用余弦函数驱动下对应的运动曲线,由于卫星处于太空中的失重环境下,所受重力加速度设为0.1g,可折展防御装置的物理参数如表2所示。

表2 可折展防御装置各防护层物理属性
在防护机构折展过程中,各防护层做绕质心的转动和质心的平面运动,已知防护层质心位置,重力Gj作用方向竖直向下(X轴负向);各个关节铰的运动规律和防护层质量及绕质心的转动惯量已知,通过对系统建立式(9)所示Lagrange动力学方程,可求得驱动关节铰运动的驱动力矩。现设各防护层质心代号为1、2、3,求解过程为
(9)
τi为关节铰广义驱动力矩;L为Lagrange函数,L=K-P,K为系统总动能,P为系统总势能。防护机构系统动能表达式为
(10)
0xmi为防护层质心在基座标系中X0方向坐标;0ymi为防护层质心在基座标系中Y0方向坐标;θi为防护层在基座标系中的转角;Ji为防护层i关于其质心的转动惯量。
基础坐标系中各防护层质心速度坐标为:
(16)
将各个防护层的质心速度公式代入到动能计算式(17)~式(20),可得系统各个关节铰的动能K1、K2、K3以及总动能K的表达式为:
(17)
(18)
(19)
K=K1+K2+K3
(20)
在空间失重环境下重力加速度设置为0.1g,假设重力作用方向沿基座标系X0轴负方向,则各个防护层重力势能为:
(21)
(22)
(23)
P=P1+P2+P3
(24)
通过上述公式,将可折展防御装置的动能、势能计算公式代入到Lagrange函数式(25),进行相关运算,可得到各个关节铰驱动力矩;以60°关节铰为例,将式(11)~式(16)代入到动能、势能求解式(17)~式(24),再代入至拉格朗日方程式(9),将运动学中关节铰转动角度函数代入方程进行偏导运算,可求解出随时间转动的力矩曲线。
L=K1+K2+K3-(P1+P2+P3)
(25)
折展过程中各防护层质心位移曲线如图8所示。第1防护层质心绕基坐标系做旋转运动,因此距离坐标系原点位置一直不变;第2防护层位置先保持不变,然后逐渐增大在30.1 s处达到最大值,距离基坐标系原点为2 145.85 mm,之后逐渐降低到达最终位置,距基坐标系原点1 862.34 mm;第3防护层质心位移曲线与第2防护层质心位移曲线趋势相似,在28.7 s达到最大值,距基座标系原点最远为2 675 mm。

图8 防护层质心位移
各防护层质心速度幅值运动曲线如图9所示。第1防护层质心速度曲线先增加后减小,呈抛物线状,在24.3 s时刻速度幅值达到峰值30.4 mm/s;第2防护层质心速度曲线与第3防护层质心速度曲线大体相似,先增加到最大值,再降低随后二次增加最后降低为0,第2防护层质心速度在16.7 s达到最大值为116.6 mm/s;第3防护层质心速度峰值为136.6 mm/s,对应时刻为16.8 s。

图9 防护层质心速度幅值
防护层质心加速度幅值曲线如图10所示。各防护层质心加速度曲线趋势存在相近的地方,第1防护层质心加速度在11.3 s后缓慢降低,在11.3~36.4 s一直处于相对平稳的状态,其加速度最大值为5.2 mm/s2;第2防护层和第3防护层加速度幅值存在局部的小范围波动,这是由模型曲线精度原因所导致的,第2防护层在运动初始阶段加速度达到最大值25.8 mm/s2;第3防护层质心加速度在加速和减速阶段加速度大小相同,且在初始阶段的加速和运动末尾的减速阶段加速度达到最大值为29.5 mm/s2。

图10 防护层质心加速度幅值
在力矩求解中,由于函数较复杂、运算量大,通过MATLAB编写各关节铰动力学方程,得到驱动力矩曲线图如图11所示。如图12所示为通过ADAMS建立的动力学模型仿真得出的驱动力矩曲线,两者对比曲线趋势、数值相似。
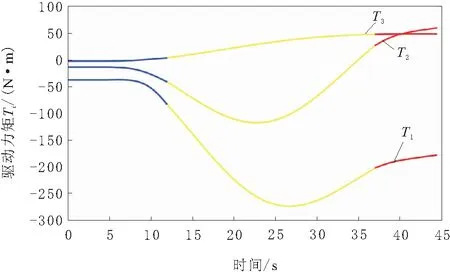
图11 关节铰力矩理论值

图12 关节铰力矩仿真值
0~4.4 s内根部关节铰所受力矩为34.32 N·m,之后数值上升,11.8 s时力矩为79.1 N·m;11.8~36.7 s力矩数值变化为先增加后减小,25.6 s力矩达到最大值264.32 N·m,在正弦加速度减速段力矩逐渐降低至171.12 N·m;中部关节铰初始力矩为10.88 N·m,在正弦加速度加速段力矩逐渐增加,在22.7 s力矩达到最大为112.3 N·m。等速运动区段力矩经过了力矩增加、减小和反向增加的过程,在等速运动区段结束时,其力矩增加到28.15 N·m,正弦加速度减速段力矩继续增加至60.31 N·m;端部关节铰初始力矩为0,之后一直增加,机构运动结束时力矩为49.42 N·m。
3 可折展防护机构驱动形式改进优化
由于上述驱动螺母采用的是正弦驱动,驱动螺母的加速度一直处于连续渐变状态,机构运动平稳,但是各关节铰链的转动一直处于加速、减速状态,会导致驱动力矩的增大,机构的运行效率降低。考虑到可折展防护机构的展开效率,降低驱动力矩,对驱动螺母的运动型是采用梯形运动[10],即采用加速-匀速-减速的运动形式,缩短机构展开时间的同时,驱动力矩做到不增加,甚至降低,因而对此运动形式下的展开进行了动力学仿真分析。
3.1 改进梯形运动规律设计
由于折展机构加速度总是处于变化状态,为提高机构的运动特性,使得效率更高,改变各个关节铰丝杠螺母驱动函数,使关节铰在等速运动区段内加速度为0,处于匀速转动状态,初始段和终止段处于加速和减速度段,机构运行将更加平稳,效率更高。丝杠螺母驱动设置如下:
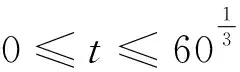
(26)
b.当3.8≤t≤30.28时,即
(27)
c.当30.28 (28) 如图13所示为驱动优化后各个关节铰力矩随时间变化曲线。根部关节铰初始力矩为34 N·m,随后逐渐增大,在19.3 s时力矩达到最大值263.4 N·m,机构运行停止时力矩大小为171.6 N·m;中部关节的铰力矩曲线趋势与根部关节铰相同,初始力矩为10.7 N·m,力矩最大值为112.2 N·m,对应时间为15.4 s;端部关节铰初始力矩为0,随着时间的增长力矩值逐渐增大,最大值为50.5 N·m。 图13 各关节力矩曲线 图14为改进前后根部关节铰力矩变化曲线。根部关节铰改进前最大力矩为264.32 N·m,改进后最大力矩为263.4 N·m,最大力矩数值相近;中部关节铰改进前后最大力矩为112.3 N·m、112.2 N·m,端部关节铰改进前后最大力矩为49.42 N·m、50.5 N·m。分析可知2种不同的驱动运动形式最大力矩数值相近,但是梯形运动的驱动形式节省了展开时间,效率提升了26.82%,可以更加快速、有效的应对空间碎片的撞击。 图14 改进前后根部关节铰力矩对比 对防护机构的运动及驱动力矩进行了研究,在确定驱动螺母运动形式后,运用D-H法建立运动学模型,对机构电磁锁定部位进行运动规律分析,由运动速度、加速度曲线可得机构折展过程理论上运动平稳可靠。针对防护机构的运动特征,通过矢量积法对电磁锁和各防护层质心的雅克比矩阵进行了求解,并与仿真结合验证了其正确性,通过ADAMS仿真得到了防护层质心加速度曲线;基于建立的动力学模型,为进一步研究关节铰链驱动力矩,根据Lagrange动力学方程,在考虑重力作用下建立动力学模型,通过MATLAB求解各时刻关节铰链力矩并与ADAMS仿真数值曲线对比,具有较高的吻合度。为提高机构运行效率,对驱动形式进行了改进,经过分析表明,改进后驱动力矩几乎不变,但机构运行时间降低了26.82%,3.2 改进前后力矩分析对比


4 结束语
