基于理性疏忽理论的交通疏散网络双层优化模型

赵传林，贺少松，孙淑敏，王钰涵

(北京建筑大学，土木与交通工程学院，北京 102616)

0 引言

台风、地震等不确定灾难的发生，以及重大活动的举办，往往要求在短时间内利用有限的交通资源，将大量人员从危险区域或活动举办地疏散出去，从而最大限度地减少对社会的不利影响，这需要交通管理者能够及时制定合理的疏散策略，科学地规划疏散路径，并执行有效的交通组织措施。关于疏散的研究引起了国内外学者的广泛关注。Cova 等[1]提出了基于车道层面的道路交通疏散路径规划模型，以出行距离最小化为目标，得到路网交叉口处的疏散交通规划方案。任刚等[2]提出网络过饱和度概念，结合交通组织疏散策略建立过饱和控制的疏散网络双层优化模型。赵星等[3]构建了基于消除交叉冲突的疏散网络优化双层模型，上层以总疏散时间最短为目标，对各车道转向进行设置，下层基于随机用户均衡原理进行路径选择。Daganzo等[4]提出了一个非预期性的、自适应的、可分散管理的疏散策略，即使由于驾驶员博弈而存在回流，该策略也被证明是最优的。Wu等[5]提出一个直观的、非预期性的、部分分散管理并且自适应性的组合疏散策略，用于在有限输入的情况下管理疏散路线，从而最小化系统疏散时间。考虑疏散者是有限理性的，安实等[6]基于意向行为调查数据验证了应急疏散者是后悔规避的，而非预期效用最大化；任其亮等[7]通过计算“有效备选路径”的前景值，建立了基于前景理论的应急交通疏散路径选择模型。

最近，Jiang等[8]将理性疏忽理论应用于交通分配模型的研究中，建立了基于理性疏忽理论的路径选择模型，并给出理性疏忽用户均衡条件。目前鲜有研究将理性疏忽理论应用于交通网络疏散问题的研究中。理性疏忽理论最早由诺贝尔经济学奖获得者Sims在2003年提出[9]，大多应用于行为经济学的研究中，认为决策者处理信息的能力是有限的，并且获取、处理信息需要成本。对于交通网络疏散问题，疏散者在面临交通信息时，更可能没有时间和精力去处理各类信息，而是会理性地选择疏忽某些相对不重要的信息。基于此，本文将研究基于理性疏忽理论的交通网络疏散问题。考虑疏散网络交通状态的随机性和出行者信息处理能力的有限性，建立双层优化模型并设计求解算法，然后通过算例验证模型的有效性。研究成果可以为疏散策略的制定提供参考依据。

1 双层优化模型

本文假设条件包括以下3条：

(1)各路段的出行时间仅与该路段自身交通量有关，与其他路段交通量无关；

(2)疏散路网的背景交通量很小；

(3)出行者在路径选择过程中遵守规划者的疏散策略，在此基础上根据个人情况自主选择路径。

1.1 上层模型

上层模型以系统总疏散时间最小为目标函数，将路段是否单行作为决策变量。疏散路网G(N,A)中节点集和路段集分别用N(n∈N)和A(a∈A)来表示，a(i,j)表示连接节点i和节点j的路段a，上层模型的决策变量为路段单行参数φa，优化目标为系统总疏散时间Q(φa)最小。

目标函数为

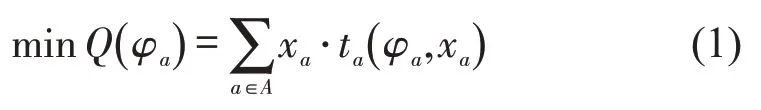
约束条件为

式中：xa为路段a上的交通量；ta(φa,xa)为路段a上的出行时间，是关于φa和xa的函数。式(2)为单行参数的设置，对应不同的疏散策略；式(3)为非负条件。

本文考虑3 种策略：最优单行策略，即根据所建立的疏散网络双层优化模型的最优解而确定的某些路段设置为单向通行；非单行策略，即所有路段保持原先的双向通行；全单行策略，即将所有路段都改为单向通行。由上层模型确定的路网单行策略(即哪些路段设置单行，哪些路段保持不变)，将传递给下层模型，进行下层模型的求解。

1.2 下层模型

下层是基于理性疏忽理论的路径选择用户均衡模型，疏散起点和终点分别用r和s表示。参考文献[8]，基于理性疏忽理论的用户均衡条件为

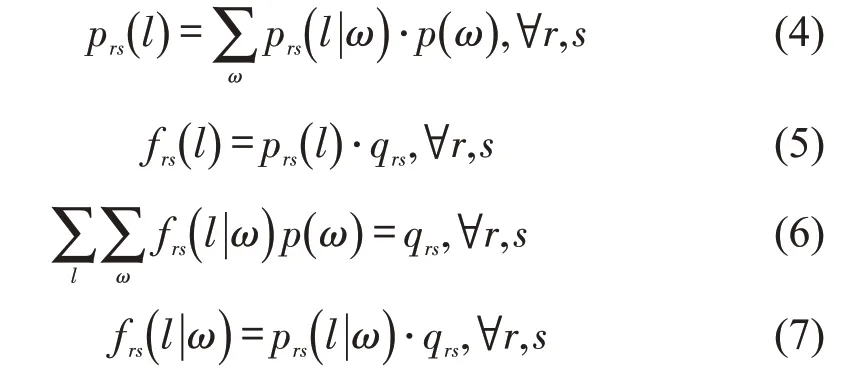
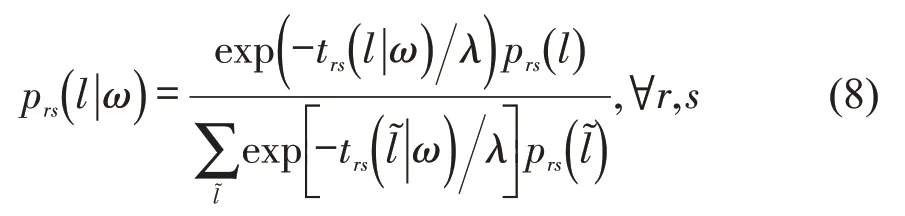
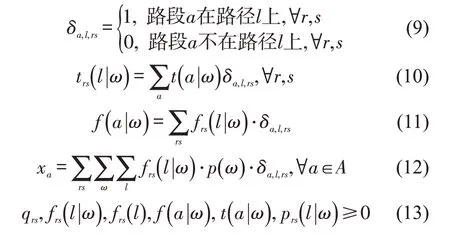
约束条件为式中：prs(l|ω)为在状态ω下选择路径l的条件概率，计算公式如式(8)所示；trs(l|ω)为在状态ω下路径l的出行时间；λ为单位信息成本；为泛指的路径l；p(ω)为状态ω的概率，状态可以描述交通系统的不确定性，可用出行时间、通行能力等表示；qrs为疏散点对rs的待疏散量；frs(l|ω)为在状态ω下分配在路径l上的交通流量，由式(7)计算得到；t(a|ω)为状态ω下路段a上的出行时间，采用改进的BPR函数对其进行计算，即

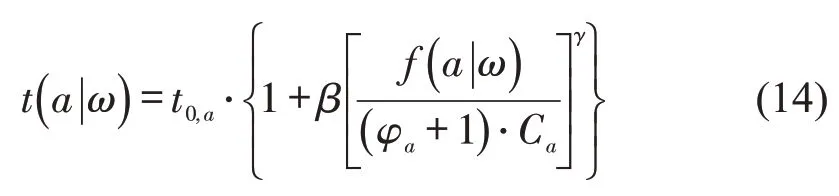
式中：t0,a为路段a的自由流时间；f(a|ω)为状态ω下路段a的交通流量；Ca为路段a的原始通行能力；β和γ为公式参数。当φa取1时，路段a在节点i→j方向设置单向通行，此时通行能力变为原来的2倍；当φa取0时，表示路段a保持双向，此时通行能力不变；当φa取-1时，表示路段在节点i→j方向不可通行，此时路段a的出行时间为无穷大。可以得到路段a上的出行时间公式为

式(4)表示均衡时选择路径l的无条件概率公式；式(5)表示均衡时分配在路径l上的交通流量；式(6)表示针对某疏散点对rs，待疏散量等于分配在路网中所有路径上的流量之和；式(9)中δa,l,rs为关于路径和路段关系的0-1变量，若路段a在路径l上则取1，否则取0；式(10)为计算在状态ω下路径l上的出行时间；式(11)为计算在状态ω下分配在路段a上的交通流量；式(12)计算整个疏散网络上每个路段的流量，进行算法设计时需要将该值返回给上层模型；式(13)为非负条件。需要说明的是，由式(4)～式(15)定义的理性疏忽用户均衡条件的解是存在的，其证明过程参见文献[8]。

2 求解算法

双层规划问题属于NP-hard 问题，其求解多采用非数值优化算法，基于迭代产生较优的全局解。粒子群优化(Particle Swarm Optimizer,PSO)算法是一种基于群智能(Swarm Intelligence)方法的演化计算技术，受人工生命的研究结果启发，PSO 的基本概念源于对鸟群捕食行为的研究。PSO中，每个优化问题的潜在解都是搜索空间中的一个粒子，所有粒子都有一个适应值(通常为待优化目标函数)，对应到本模型中，每个粒子都代表着一个单行策略，其适应值代表上层模型中的目标函数值(即系统总疏散时间)，每个粒子有速度属性和位置属性，PSO初始化为一群随机粒子，然后通过迭代找到最优解。假设粒子群规模为Ψ，粒子序号i，i=1,2,…,Ψ，粒子的维度D，对应本文上层模型中决策变量的个数，即路网中路段的个数，d为粒子维度序号或路段序号，k为迭代次数，为了增加搜索的随机性，设置r1和r2为区间[0,1]内的随机数。

粒子速度更新公式为

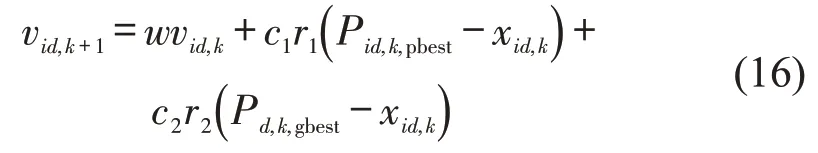
粒子位置更新公式为

式中：w为惯性权重；c1为个体学习因子；Pid,k,pbest为粒子i在第k次迭代中第d维的历史最优位置；c2为群体学习因子；Pd,k,gbest为群体在第k次迭代中第d维的历史最优位置，对应本问题中第k次迭代时当前最优单行策略的系统总疏散时间；xid,k为粒子i在第k次迭代中第d维的位置，对应本问题中第k次迭代时某单行策略的系统疏散时间，

式(16)中粒子速度由3部分组成：第1部分为粒子的惯性部分，由惯性权重w和粒子自身速度构成，表示粒子对先前自身运动状态的信任；第2 部分为粒子的认知部分，表示粒子本身的思考；第3部分为群体部分，表示粒子之间的信息共享与合作，来源于群体中其他优秀粒子的经验。

基本粒子群优化算法主要针对连续函数进行搜索运算，但本文属于离散变量优化问题，为了在计算上保留基本粒子群算法在速度更新中的连续运算规则，将离散变量转化为连续变量后再使用粒子群优化算法[10]，本文将基于连续空间的离散粒子群优化算法(Discrete Particle Swarm Optimization，DPSO)与逐次平均法(Method of successive averages,MSA)相结合，在代码程序中采用取整的方法对离散变量进行处理，针对路网中某疏散点对，设计了DPSO-MSA启发式算法。

Step 0 初始化粒子群参数。设置粒子群规模、粒子维度、最大迭代次数、惯性权重、学习因子等参数。

Step 1 采用取整的方法处理离散变量得到初始单行参数φa，随机初始化粒子的位置和速度，粒子的个体历史最优位置Pid,0,pbest设置为粒子的初始位置，随机地将Pid,0,pbest中某个位置设置为群体历史最优位置Pd,0,gbest。

Step 2 按照式(16)和式(17)更新每个粒子的速度和位置。

Step 3 利用MSA 算法求解下层基于理性疏忽出行者的路径选择模型。

①设置理性疏忽出行者的初始信息策略矩阵P(L|ω)，由式(4)和式(5)得到各路径的初始无条件概率p0(l)和初始交通流f0(l)；

②根据上层模型中传递的路段单行参数φa和交通流fk(l)，以及式(14)和式(15)计算路段出行时间成本ta，根据式(12)可得到各路段流量xa，将ta和xa返回给上层模型。

③计算下降方向，由式(8)和式(4)计算各路径的条件概率公式pk(l|ω)和无条件概率公式；

Step 4 粒子适应度评价。将下层模型返回的xa和ta代入到上层模型的目标函数中，计算出每个粒子的适应度值。

Step 5 更新每个粒子的个体历史最优位置Pid,k,pbest，以及粒子群的历史最优位置Pd,k,gbest。

Step 6 收敛检验。若上一次迭代后最优解的适应度值与本次迭代后最优解的适应度值之差满足设置的精度，或者达到最大迭代次数，则停止优化，得到路网的最优单行策略；否则返回Step 1。

本文疏散网络双层优化模型的求解算法流程如图1所示。

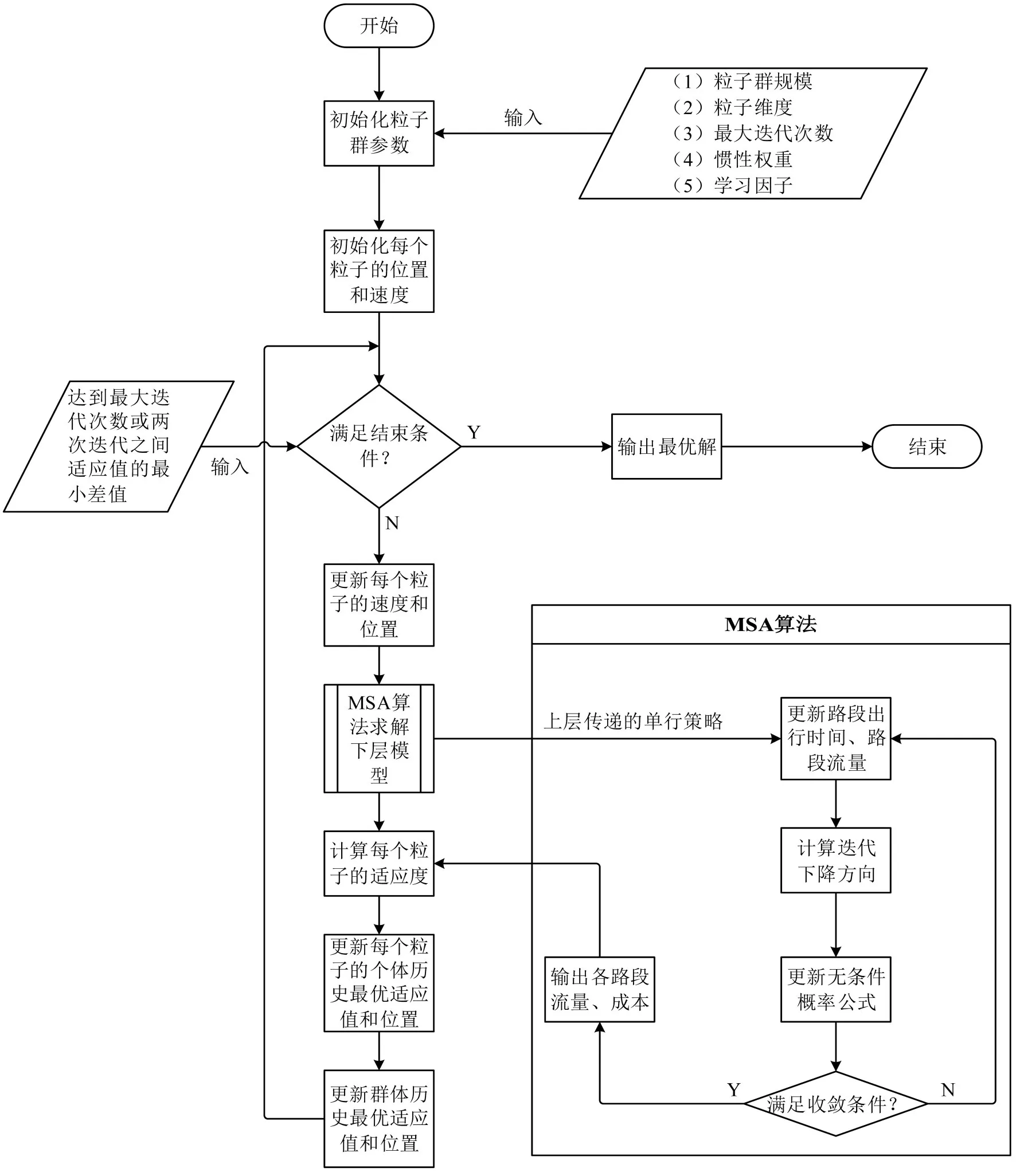
图1 算法流程图Fig.1 Algorithm flow chart

3 算例

3.1 算例描述

假定待疏散人数为3000 人。采用如图2所示的有向路网，包含9 个节点和12 条路段，每个路段都有两个通行方向，且两个方向车道数相同，路段参数如表1所示。假设每个路段存在两个交通状态，即“好的状态ωg”“坏的状态ωb”。“好的状态”对应95%的原通行能力，“坏的状态”对应50%的原通行能力，各路段两个交通状态对应的通行能力如表2所示。12条路段对应整个路网存在4096 个状态，假设状态分布服从均匀分布。针对本路网中的OD疏散点对，所有疏散路径可以直接枚举出来，如表3所示。

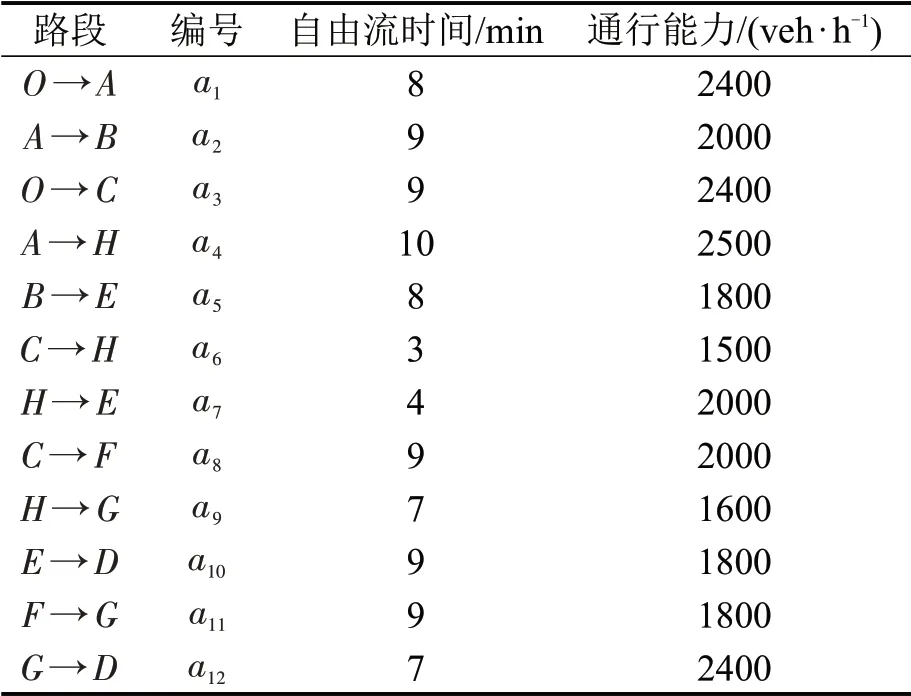
表1 各路段参数Table 1 Parameters of each link

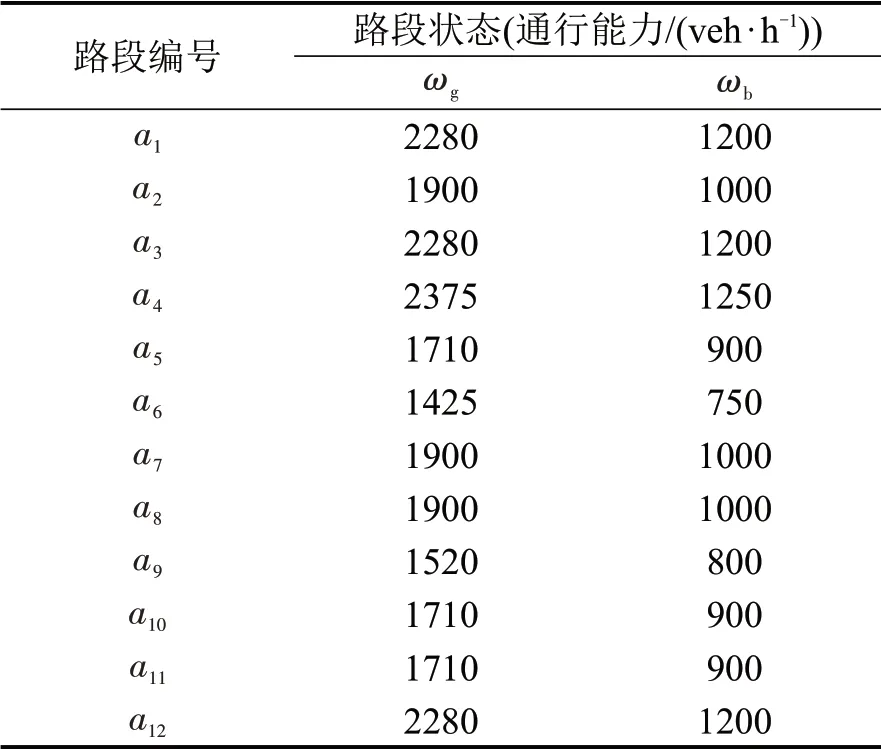
表2 各路段状态值Table 2 State value of each link

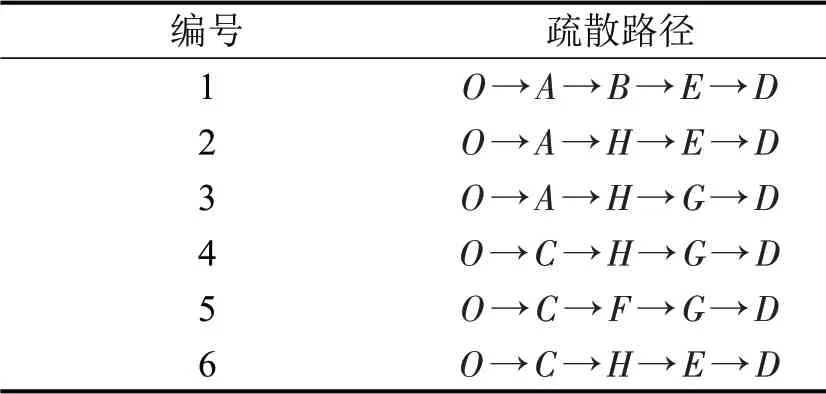
表3 疏散路径Table 3 Evacuation paths

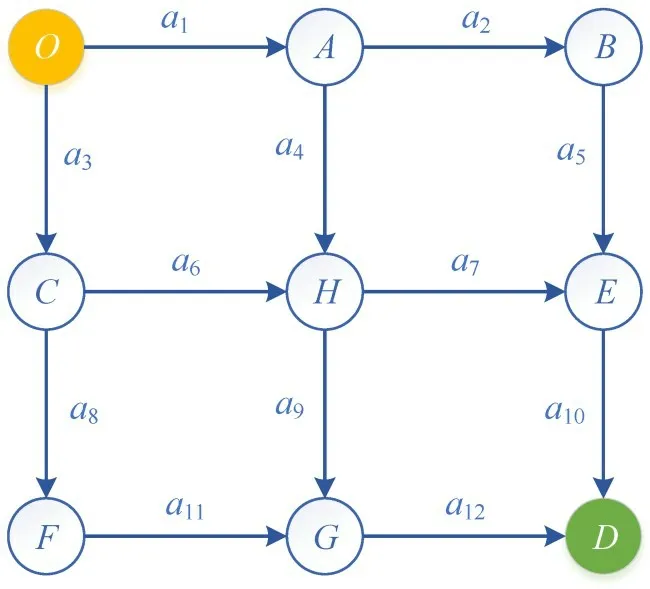
图2 疏散网络Fig.2 Evacuation network

DPSO 算法的各个参数如表4所示，MSA 算法中最大迭代次数设置为1000 次，迭代精度ρ取0.01，改进的BPR函数中参数β=0.15，参数γ=4。

表4 DPSO算法参数Table 4 DPSO algorithm parameters

3.2 结果分析

当待疏散人群的单位信息成本取值为40 时，得到路网疏散的最优单行策略为：φa1=1，φa2=1，φa3=0，φa4=0，φa5=1，φa6=0，φa7=0，φa8=0，φa9=1，φa10=1，φa11=0，φa12=1，即将路段a1、a2、a5、a9、a10、a12改为单向交通，其余路段保持双向通行，系统总疏散时间为161973.997 min。粒子群优化的历代群体最优值变化如图3所示，在此最优单行策略下，通过MSA 算法迭代的结果如图4所示，信息成本为0.0350，出行时间成本为32.453，出行总成本为32.489。图3和图4的结果说明，粒子群算法在求解本文的离散变量优化问题时体现了良好的稳定性和适用性。

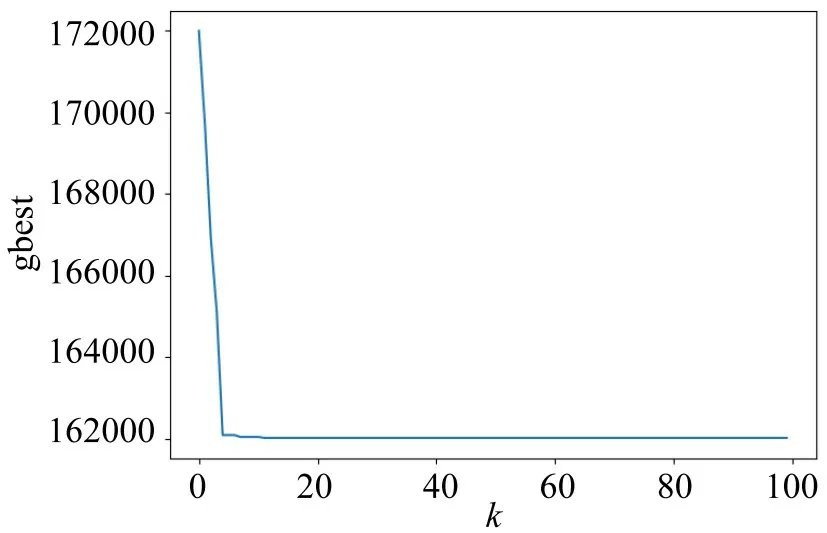
图3 历代群体最优值变化图Fig.3 Variation diagram of optimal value

图4 gap值变化图Fig.4 Gap value variation diagram

若采取非单行策略，系统总疏散时间为175627.6954 min，比最优单行策略的系统总疏散时间多了7.774%，证明将路网中部分路段设置为单向交通是利于疏散的；而采用全单行策略时，系统总疏散时间为168941.179 min，比最优单行策略下的系统总疏散时间多了4.124%，所以将路网中所有路段容量同时增大时并不一定能缩短总疏散时间，这验证最优单行策略有效性的同时，也证明了“Braess诡异现象”的存在。需要说明的是，由于粒子群算法本身的随机性，以及理性疏忽用户均衡解的非唯一性[8]，使得本文建立的DPSO-MSA算法在探索最优解的过程中，存在最优解不唯一的情况，但最优目标函数值是唯一的。

3.3 敏感度分析

针对单位信息成本λ进行敏感度分析。当λ在20～90之间变化时，得到最优单行策略下各路段使用情况如图5所示，路段a1、a2、a9、a10、a12的使用频率明显高于其他路段，这可以作为重要路段的判别依据，也可以为疏散管理者制定疏散策略时提供参考依据。最优单行策略下理性疏忽出行者的信息成本和系统总疏散时间的变化关系如图6所示，两者的变化趋势几乎一致，信息成本曲线的变化率体现了出行者获取信息量的大小，即随着λ的增加，出行者获取的信息量减少，对应的系统总疏散时间下降，也就是说，对于整个系统而言，信息量的减少反而有利于疏散，出行者获取的信息并非越多越好；当λ＞60 时，此时通过降低出行者获取信息量来减小系统总疏散时间的效果减弱。

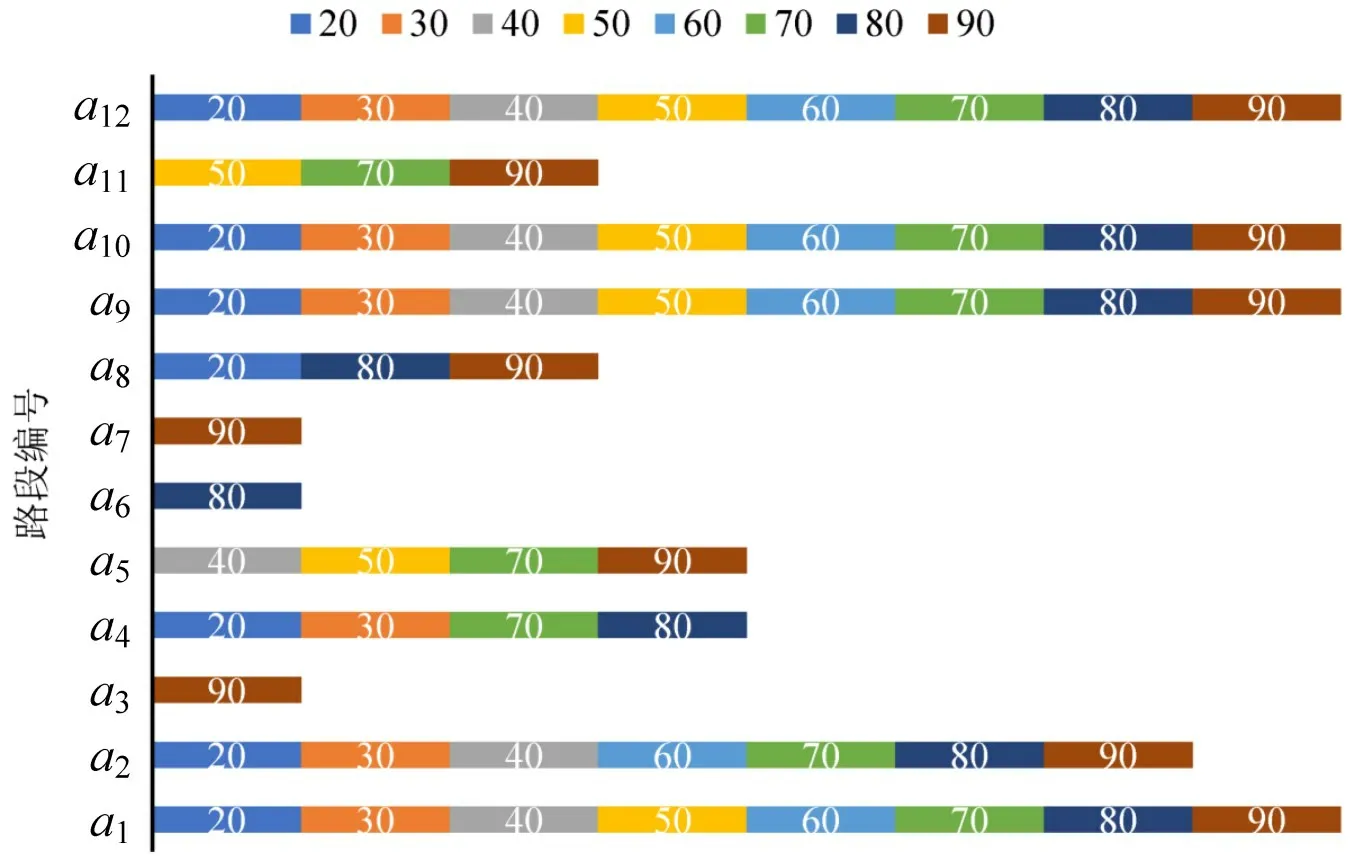
图5 最优单行策略下各路段使用情况Fig.5 Usage of each link

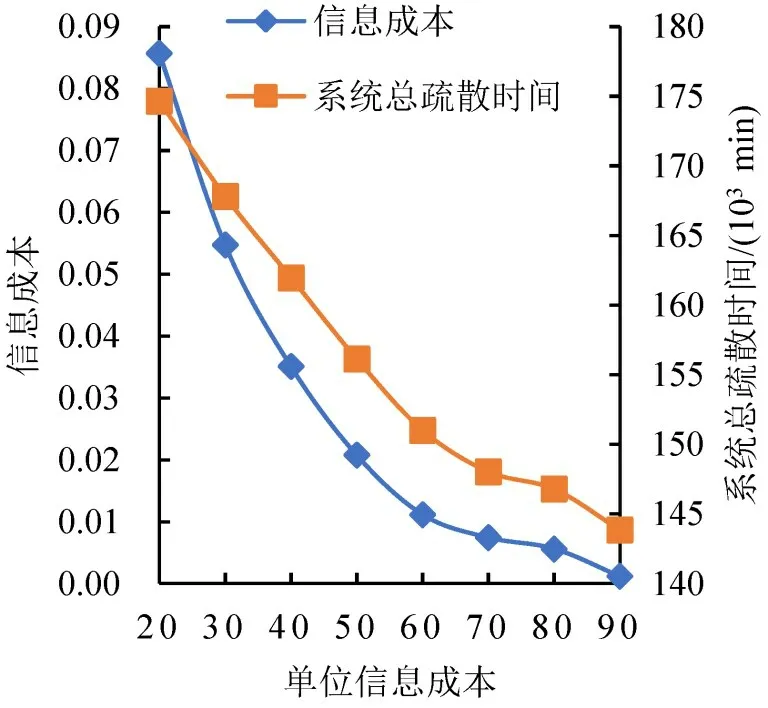
图6 最优单行策略下信息成本与系统总疏散时间变化Fig.6 Change of information cost and total evacuation time of system

将最优单行策略与全单行策略和非单行策略下的系统总疏散时间进行对比，如图7所示，当λ＜40 时，非单行策略出现不收敛现象，具体原因还有待后续深入研究。对于所有的λ值，三者的系统总疏散时间关系为，最优单行策略＜全单行策略＜非单行策略，通过本文双层优化模型得到的路网最优单行策略的疏散效果均优于其他两者，证明了模型的有效性。且随着λ的增大，最优单行策略与全单行策略越来越接近，所以当出行者所获取的信息量非常少时，可以将所有路段改为单向通行，同样可以取得与最优单行策略相当的效果。

图7 3种策略下的系统总疏散时间Fig.7 Total evacuation time of system under three strategies

4 结论

基于理性疏忽理论，本文建立了疏散网络双层优化模型，并设计了DPSO-MSA 启发式混合算法进行模型的求解。算例部分搭建了一个包含4096个交通状态的有向路网。结果表明，本文模型得到最优单行策略的系统总疏散时间比非单行策略下的系统总疏散时间少了7.774%，比全单行策略下的系统总疏散时间少了4.124%，证明本文模型有效性的同时，也验证了“Braess 诡异现象”的存在。通过对单位信息成本进行敏感度分析，识别到了疏散网络中的关键路段。还发现，随着单位信息成本的增加，出行者获得的信息量减少，系统总疏散时间也在逐渐减少，也就是说，对于整个疏散系统而言，信息量的减少反而有利于疏散，并不是出行者获取的信息越多越好，且随着单位信息成本的增大，全单行策略的疏散效果与最优单行策略越来越接近。本文模型的疏散时间是基于静态的BPR 函数，考虑疏散时间的动态性，疏散者的单位信息成本的异质性，以及单位信息成本取值的标定将是下一步研究的重点。