基于图像处理的集料颗粒特征参数研究*
2022-04-26林海翔洪嘉希殷作耀
林海翔 洪嘉希 荣 鑫 殷作耀
(1.福建省铁拓机械股份有限公司 泉州 362000; 2.沈阳铁路信号有限责任公司 沈阳 110026;3.长安大学道路施工技术与装备教育部重点实验室 西安 710064)
道路建筑材料中,混凝土的性质将直接决定道路建设的好坏。在水泥混凝土中,集料的含量有70%~85%,而在沥青混合料中集料的含量更是高达90%~95%,集料的形态特征将直接影响混合料的路用性能[1]。因此,对集料性质的研究是路面性能研究的重点。
当前已有不少专家学者采用数字图像处理技术对集料颗粒对混合料的影响进行了探究,取得了较好的成果。王文真等[2]基于统计学方法研究了粗集料各形状特征参数的分布规律,分析了各形状特征参数与级配的相关性并进行评价;耿超[3]使用一种分析集料几何特征的装置,对不同档位的集料颗粒形态特征进行定量评价和分析;秦雪[4]对不同类型集料进行了二维和三维形状特征分析,并进行了力学试验验证;汪海年等[5]利用自行研制的粗集料形态特征研究系统,提出粗糙度与分形维数2个指标对粗集料的棱角特征进行评价;李强等[6]结合CT扫描技术和有限元方法建立虚拟间接拉伸试验,从而评价粗集料形态特征对沥青混合料抗拉性能的影响;叶奋等[7]选取平面形状系数、圆度及分形维数3个粗集料形态特征参数,基于数理统计进行非参数检验,得到其分布规律及参数值;张肖宁等[8]采用激光三角测量技术对路面常用的粗集料表面微观纹理进行测量,对各表面轮廓线及其所对应的原始数据采用多种分维计算方法进行分析。
目前已有方法对于集料特征参数如扁平度、矩形度等,往往只采用一些定性的描述,缺乏定量的指标,而且分析的集料颗粒数量样本过少,代表性较差。因此本文提出一种集料颗粒二维简易采集分析装置,结合图像处理技术,对某一批次的集料颗粒扁平度、矩形度、形状因子、整体轮廓系数、粗糙度、棱角度,以及分形维数等特征参数分布情况进行整体研究,并进一步分析各参数指标与集料级配的关系,为判断混合料加工合格性、级配范围分布情况及路用性能提供理论依据。
1 研究方法
1.1 原材料
首先对0~19 mm的集料进行图像分析,集料采用石灰岩,其特征参数见表1和表2。
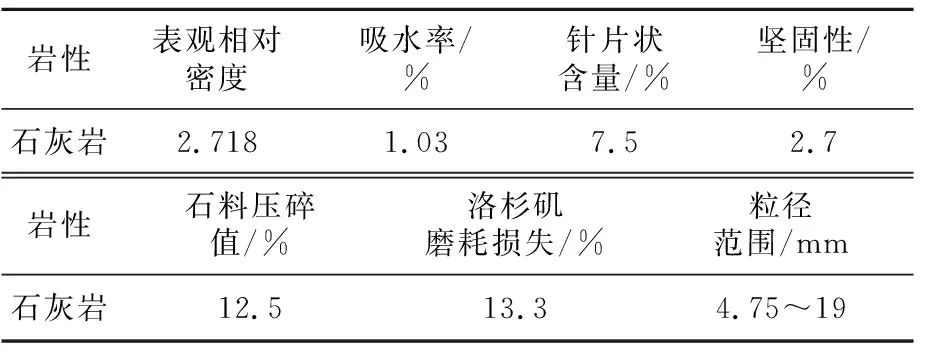
表1 石灰岩粗集料的指标
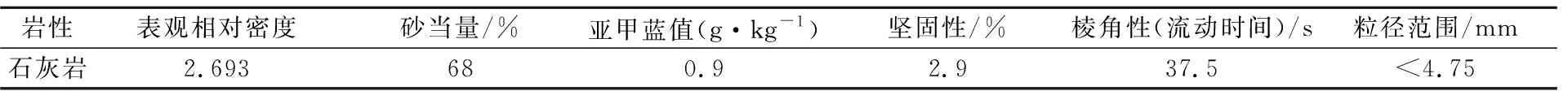
表2 石灰岩细集料的指标
1.2 试验流程
分别对同一批集料的粗集料和细集料进行特征参数的采集。在采集时,将集料随机撒布,待集料稳定后,对其最终投影面进行特征参数的采集。根据统计学规律,集料样本越大,得出的统计结果越接近真实情况[9]。本文选取的样本数量见表3。

表3 石灰岩集料的样本数量
首先,将试验原材料进行筛分,得到不同粒径范围的集料;其次将集料清洗干净,用烘箱烘干;最后,分别将不同粒径范围的集料分别均匀撒布在LED光源上,采集集料图像。
试验装置包括: MV-EM200M的CCD相机、BT-23C1214MP5的镜头(像素1 600×1 200)、LED光源、模拟控制器及面阵实验架。固定面阵实验架,使相机保持水平,将LED光源放置在镜头下,调节实验架高度至30 cm,保证光源发光面全部在镜头视野内,调节LED光源电压及镜头焦距,保证最佳的成像效果,且不能有阴影出现,避免影响读数的准确。将标定物放置在光源上,测量出此时标定物直径,并计算此时的标定系数,以此标定系数计算集料的真实粒径,如式(1)所示。
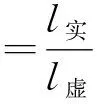
(1)
式中:l实为标定物的实际直径,mm;l虚为标定物成像的直径,mm。
1.3 图像处理
在获取试验集料图像后,使用MATLAB软件对图片进行处理,获取集料颗粒一次特征参数,见表4。
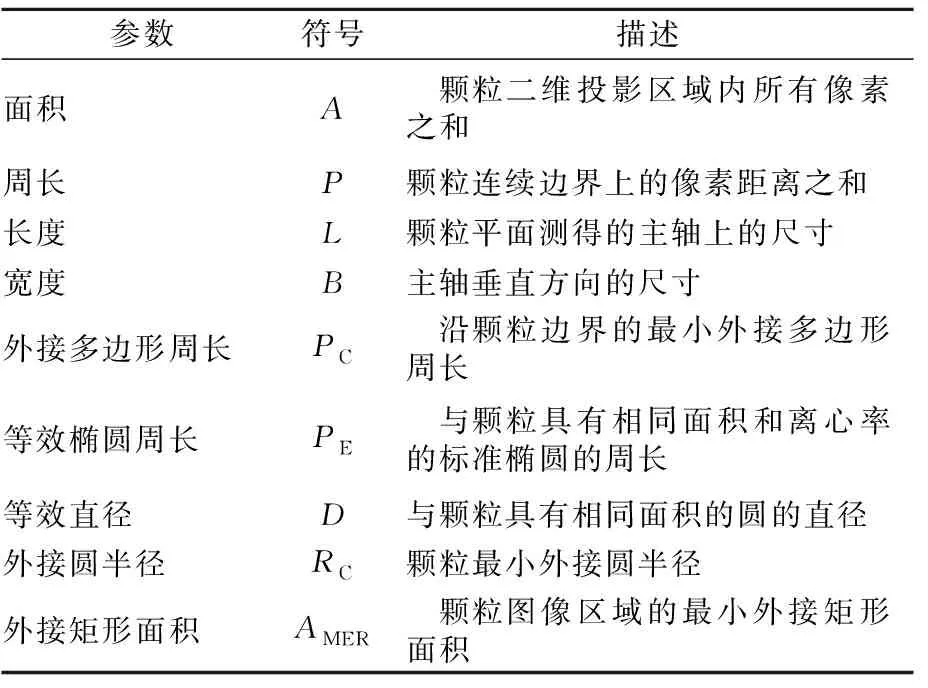
表4 集料一次特征参数
通过计算从而进一步计算集料图像的扁平度、矩形度、整体轮廓系数、形状因子、粗糙度、棱角性等二次特征参数。
首先将采集到的原始图像进行灰度化操作,然后通过MATLAB将Sigma=2,大小为5×5的Gaussian滤波作为采集到的集料图片的预处理模板(见图1),对图片进行降噪,再对图像进行二值化形态学操作,最后进行图像像素的翻转得到预处理后的图像,通过一系列处理能够减小外界因素对颗粒参数提取的影响,从而得到二值化无噪声的图像。图像处理流程见图2。

图1 Gaussian算子滤波模板
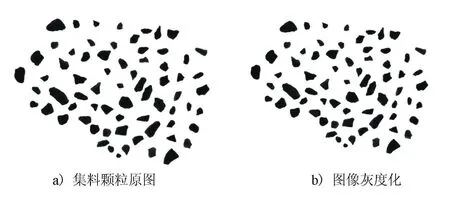
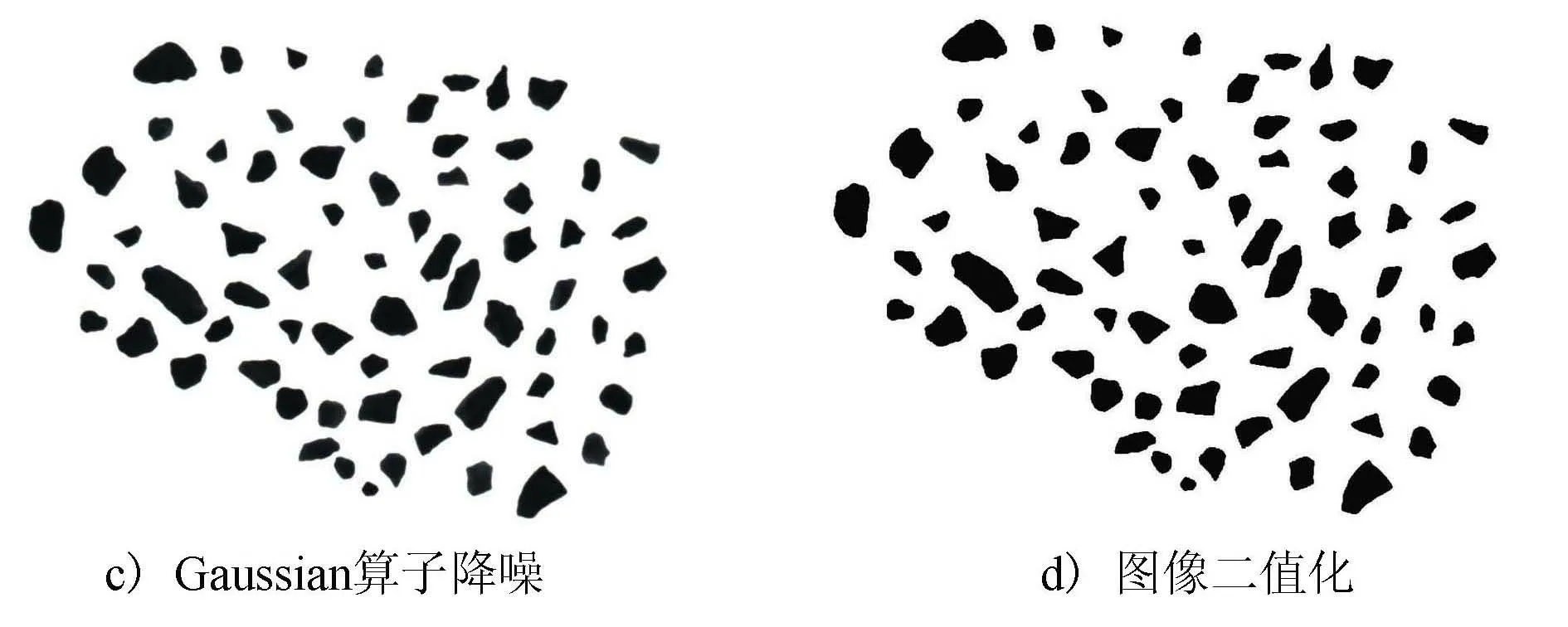

图2 图像处理流程
将现有的Sobel梯度算子直接作为边缘检测的算子,实现图像的边缘检测,见图3。为获取每颗集料颗粒的形状特征参数,采用矩形框和凸包标记等方式进一步处理集料图像,见图4。
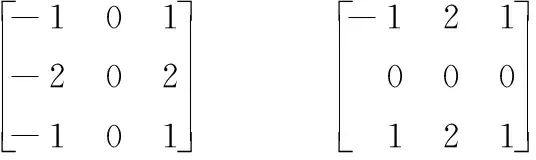
a) 模板1 b) 模板2

图4 集料特征标记
2 结果及分析
2.1 集料形状特征参数
1) 扁平度。
(2)
式中:L为颗粒主轴尺寸;B为与主轴垂直方向尺寸;e为扁平度。扁平度反映了颗粒的延长属性,e取值越大,颗粒轮廓越扁平、狭长,e≥1。
2) 矩形度。
(3)
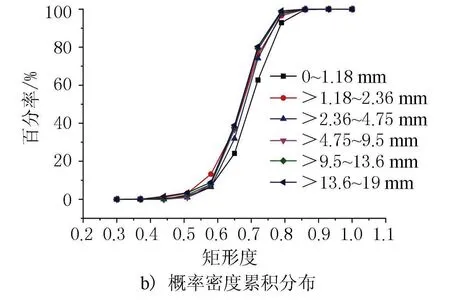
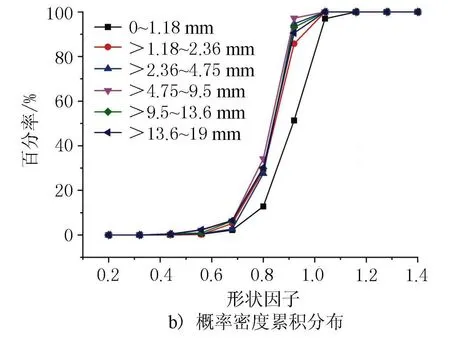
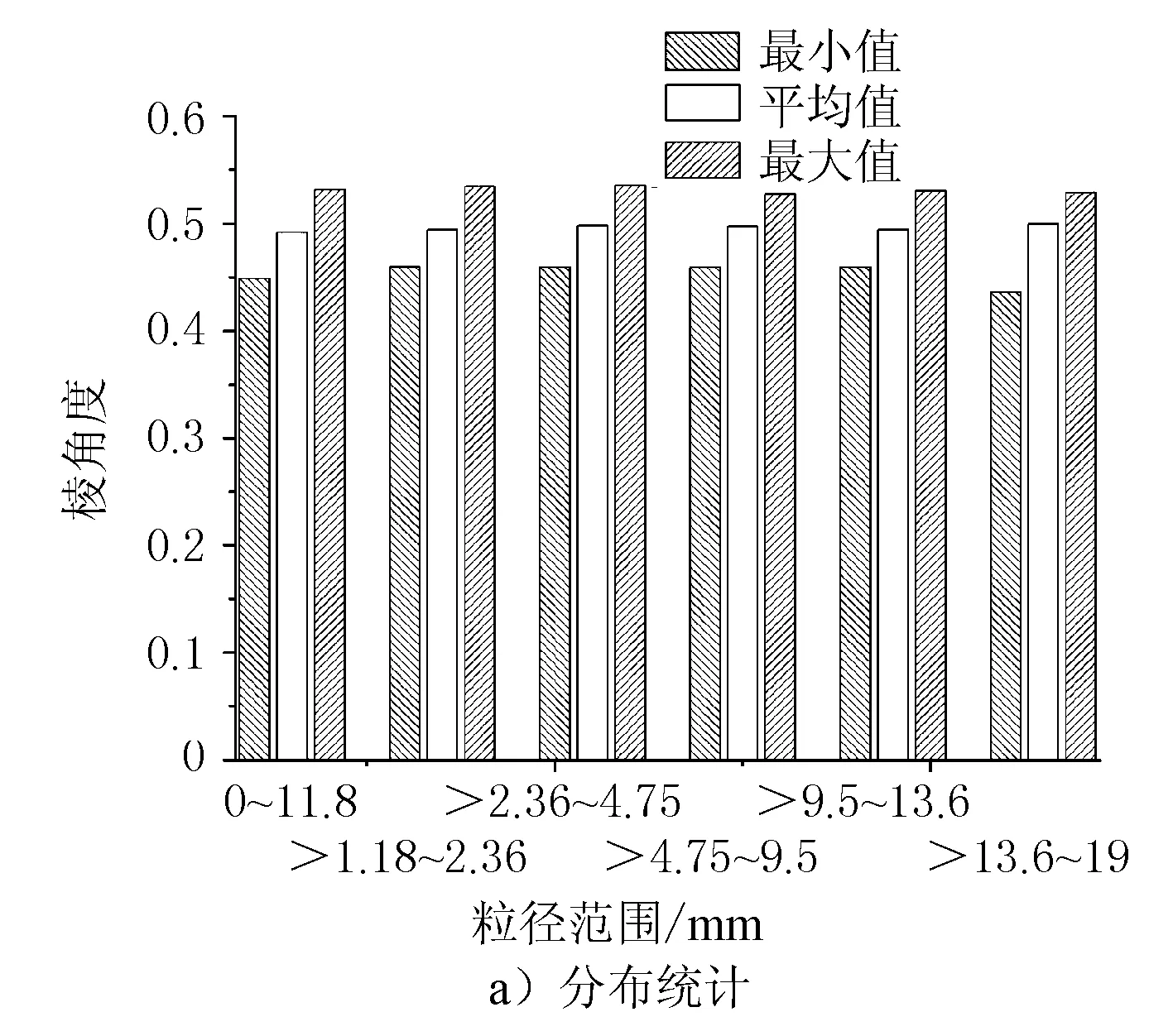
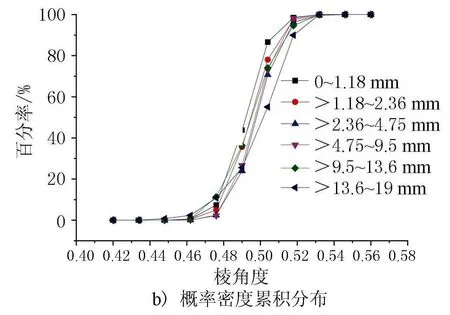
式中:A为颗粒二维投影面积;AMER为最小外接矩形面积;R为矩形度。R反映的是集料二维平面对最小外接矩形的充满程度,当图像为矩形时,R=1;当图像为圆形时,R=π/4;一般0 3) 形状因子。 (4) 式中:P为颗粒周长;F为形状因子。当颗粒形状为圆形时,F=1。F值越大,说明颗粒轮廓形状越接近圆形;一般F≤1。 4) 整体轮廓系数。集料的整体轮廓系数是描述集料整体形貌特征的重要参数,定义为等效面积圆周长与集料轮廓周长之比 (5) 式中:D为等效直径;α为整体轮廓系数。0<α≤1,α趋向于1时,集料轮廓越趋向于圆。在面积一定的情况下,整体形状越偏离圆形,颗粒的突出棱角及粗糙起伏度越大,颗粒周长越大,α值越小。 5) 粗糙度。 (6) 式中:PC为外接多边形周长;r为粗糙度。 6) 棱角度。 (7) 式中:PE为等效椭圆周长;Ag为棱角度。棱角度主要是用于表示颗粒表面的棱角数目及突出程度。 7) 分形维数。 (8) 式中:d为分形维数;ε为小立方体一边的长度;N(ε)为用此小立方体覆盖被测形体所得的数目。d用于反映颗粒的不规则性。 采用最小外接矩形框短边长度对集料颗粒粒径进行衡量,根据标定系数k标,将图像中集料粒径转换为真实粒径。根据数理统计原理进行统计分析,对不同粒径范围的石灰岩集料的总体特征参数进行计算。集料二次特征参数的分布结果及其概率密度累积分布见图5~图10。 图5 扁平度参数统计分布结果 由图5a)可见,不同粒径范围集料颗粒的扁平度均值随着粒径范围的增加呈现递增的状态。由图5b)可见,13.2~19 mm粒径范围集料颗粒的扁平度概率密度累积分布曲线较曲折,其余粒径范围集料颗粒分布地较平缓,集料颗粒扁平度主要集中在0.6~1.4之间。 图6 矩形度参数统计分布结果 由图6a)可见,不同粒径范围集料颗粒的矩形度平均值变化幅度很小,变化幅度小于6%,说明各粒径范围集料颗粒的矩形度差异性较小。由图6b)可见,集料颗粒矩形度主要集中在0.6~0.75之间,颗粒的概率密度累积分布接近“S”形曲线中线,说明集料矩形度分布较均匀。 图7 形状因子参数统计分布结果 由图7a)可见,集料颗粒的形状因子平均值随着粒径范围的增大而减小,说明随着集料粒径的增大集料颗粒形状差异性减小。由图7b)可见,集料颗粒形状因子主要集中在0.69~0.89 mm之间,0~1.18 mm集料颗粒概率密度累积分布较为曲折,说明形状差异性较大,其余粒径颗粒的形状因子分布曲线随着粒径的增大逐渐趋于平缓。 由图8a)可见,不同粒径范围集料颗粒的整体轮廓系数平均值与最大值变化呈现出一致性,且与形状因子呈现出相同的递减性,说明随着集料颗粒粒径的增大,集料颗粒整体轮廓系数差异性减小。由图8b)可见,整体轮廓系数主要集中在0.4~0.48 mm之间,且曲线上升速度较快,说明集料整体轮廓系数分布较为集中,集料整体轮廓系数差异性较小。 图9 粗糙度参数统计分布结果 由图9a)可见,集料颗粒粗糙度随着粒径范围的增大而增大,但增长幅度变化不大。由图9b)可见,集料颗粒粗糙度主要集中在0.98~1.01 mm,占比达到85%以上,说明集料颗粒粗糙度差异性较小。 图10 棱角度参数统计分布结果 由图10a)可见,集料颗粒棱角度最小值、平均值及最大值在不同粒径范围内差异性较小,且均值相差小于3%,说明颗粒棱角性分布较为均匀。由图10b)可见,集料颗粒棱角度主要集中在0.47~0.52 mm之间,在0.47 mm之前、0.52 mm之后颗粒数小于5%,说明颗粒棱角度分布较为集中。 为确定集料的二次特征参数对混合料级配的影响,配置了11组具有不同粒径颗粒含量的集料,放大集料间二次特征参数的差异性,为相关性分析提供更有利的数据支撑。具体操作如下。 挑选同一批石灰岩集料的6种粒径范围,按照不同比例进行合理组合,得到11组不同级配的混合料,其级配参数见表5。 利用集料简易采集系统对上述组合进行取样测试,利用MATLAB进行处理计算,分别得到不同粒径范围组合的集料的扁平度、矩形度、形状因子、整体轮廓系数、粗糙度、棱角度及分形维数的特征参数。基于最小二乘法的线性回归模型[10-11],分析集料二次特征参数与级配之间的关系,相关性分析结果见图11~图14。 表5 不同粒径范围集料组合 图11 集料特征参数与级配相关性 图12 集料特征参数相关性 图13 集料粒径范围与分形维数关系 图14 集料级配与分形维数关系 由图11可见,矩形度、形状因子、整体轮廓系数、粗糙度及棱角度与级配均现良好的相关性,其相关性指数R2分别为-0.990 94、-0.996 97、-0.995 9、0.992 95及0.963 99。由于扁平度反映的是集料内针片状的情况,针片状颗粒越多,级配越不稳定,故扁平度与级配的相关性较差,仅为0.762 38。 扁平度与级配的关系为:flatness=0.008 68×(particle size)+1.092 79;矩形度与级配的关系为:rec=-0.005 62×(particle size)+0.698 7;形状因子与级配的关系为:shape=-0.031 68×(particle size)+0.929 47;整体轮廓系数与级配的关系为:contour=-0.010 04×(particle size)+0.484 75;粗糙度与级配的关系为:roughness=0.023 16×(particle size)+0.941 96;棱角度与级配的关系为:angularity=0.000 392 4×(particle size)+0.492 01。随着集料粒径的增大,即混合料级配逐渐变粗时,扁平度、粗糙度及棱角度逐渐变大,矩形度、形状因子及整体轮廓系数逐渐变小,说明在前3个参数越大及后3个参数越小时,集料级配越粗。此外,由图12可以进一步看出,这6个特征参数间的相关性。如图12所示,扁平度只与棱角度相关性关系较好;而其余5个特征参数间相关性关系均较好。因此,可以用上述6个参数来表征级配的粗细程度,判断混合料配比情况,并为混合料级配设计提供理论依据。 由图13可见,集料的分形维数在同一粒径范围内具有相似性。随着粒径范围的增大,分形维数随之增大,且稳定在一个新的范围内。由图14、图15可见,集料粒径与分形维数的相关性指数为R2=0.981 85,相关性方程为fractal=0.090 33×(particale size)2-0.002 56×(particle size)+1.035 5;分形维数随着级配粒径的增大而增大,说明集料粗糙程度逐渐增大,越有利于提高路面抗滑性能,也符合实际应用情况。因此,可以用集料级配的整体分形维数来表征集料级配的粗糙及粗细程度,从而为集料抗滑性能情况提高理论依据。 1) 本文选用石灰岩集料,采集了不同粒径范围集料的面积、周长、矩形框长度、宽度、分形维数等一次特征参数,通过对其进一步分析得到了扁平度、矩形度、形状因子、整体轮廓系数、粗糙度及棱角度等二维特征参数。并进行了统计分析试验,结果表明不同粒径范围的石灰岩特征参数具有一定的统计规律。 2) 形状因子、整体轮廓系数、粗糙度及棱角度在所有特征参数中差异性较小,且集料颗粒分布较为集中。除扁平度外,其余5个二次特征参数相关性较大,均达到了0.94以上。 3) 矩形度、形状因子及整体轮廓系数与集料级配呈现负相关,扁平度、粗糙度及棱角度与集料级配呈现正相关,可以以此为级配设计提供理论依据。 4) 分形维数随着集料粒径范围的增大而增大,集料粒径范围在同一范围时,分形维数相差不大,可以以此来表征集料颗粒的粗糙及粗细程度,为抗滑性能提供理论依据。2.2 集料二次特征参数统计分析


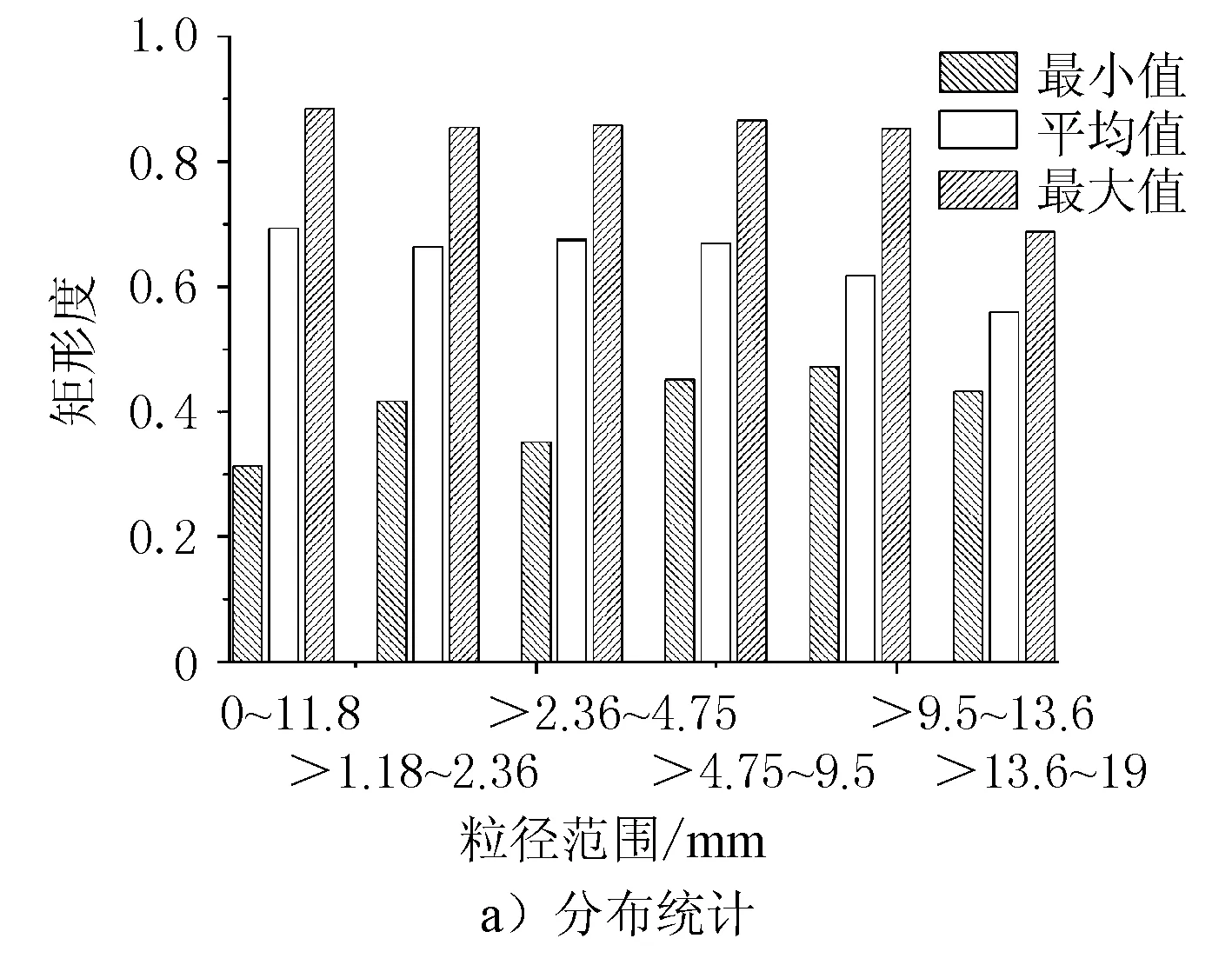




2.3 集料二次特征参数与级配的相关性




3 结论
