煤矿领导者和监管者的行为决策演化博弈分析*
2022-04-26刘纪坤
刘纪坤,黄 杰
(西安科技大学 安全科学与工程学院,陕西 西安 710054)
0 引言
煤炭行业是我国能源支柱产业,煤矿资源不断开采利用的同时也伴随着诸多生产事故。如何有效构建安全监管体系,落实安全监管工作,是解决安全管理工作问题的首要途径[1-2]。近年来,国内外学者[3-7]从经典博弈论角度出发研究了煤矿安全监管的相关问题,但经典博弈论存在固有缺陷:假设中的“完全理性”和“共同知识”,在实际情况中无法达到;经典博弈论缺乏动态变化调整。因此,有必要采取更为严谨的方法研究煤矿安全监管问题。
演化博弈论是Smith等[8]对生物进化过程进行分析时提出的,在经典博弈论的基础上引入了时间变量,研究对象是群体行为,并且假设研究对象都具有“有限理性”;Taylor等[9]在此基础上,提出了复制动态方程的概念,进一步完善了演化博弈论中的基本概念。如今演化博弈论作为一种更完善的研究方法已被广泛应用于解决煤矿安全监管问题[10-11]及工程项目的安全监管问题[12-13]。我国学者付茂林等[7]从监察机构的角度分析了存在监察变异时煤矿安全监察行为的进化稳定状态,提出监察成本、上级领导监督概率、认真监察的激励奖励是影响其稳定状态的主要因素;刘全龙[10]通过构建国家、地方政府、企业之间单边博弈、双边博弈和多方博弈探讨了我国煤矿安全监察监管的博弈变化与控制问题。
据上述相关研究发现,由于我国学者在工程管理领域引入演化博弈论理论时间较晚,且多数分析的都是宏观层面(国家与地方政府、政府与企业等),部分学者从企业内部入手进行研究(管理者与基层人员、人员自我博弈等),缺少对于企业领导决策者与监督管理者的博弈研究。为完善企业内部微观层次的演化博弈规律,本文基于有限理性的企业决策者和监督管理者,构建演化博弈模型,得到演化稳定策略(Evolutionary Stability Strategy,ESS)并分析讨论,进行数值模拟仿真进行验证,针对相关问题提出建议,为企业安全管理工作提供理论指导。
1 演化博弈模型的假设与构建
基于我国煤矿行业安全监察体制“国家监察、地方监管、企业负责”的垂直管理模式,对于演化博弈模型设定如下:
1)博弈双方主体均为大量群体,具有有限理性,且双方主体之间存在非对称博弈。领导决策者进行安全投入的概率为x,不进行安全投入的概率为1-x,x∈[0,1];监督管理者严格监管的概率为y,放松监管的概率为1-y,y∈[0,1]。
2)煤矿企业领导决策者进行安全投入所得到的收益为G1;监督管理者严格监管得到的收益为G2。领导决策者进行安全投入的费用为S;监督管理者可支配的安全项目款为s。事故发生率为γ,γ∈[0,1]。发生事故后对领导决策者和监督管理者的处罚分别为C1,C2。
3)由于煤矿企业受到多主体管理部门之间的相互影响作用,引入外部监管和舆论声誉的影响。监管部门对领导者不进行安全投入的处罚款为E;监管部门对监督者放松监管的处罚款为e。发生事故后,煤矿企业的财产损失和声誉损失总和为B。
据以上分析,构建博弈双方收益矩阵见表1。

表1 企业领导决策者和监督管理者的博弈收益矩阵Table 1 Game profit matrix of enterprise leading decision-maker and supervisor
2 模型分析
对企业领导决策者,进行安全投入的期望收益UA如式(1)所示:
UA=G1y+G1(1-y)=G1
(1)
式中:G1为领导决策者进行安全投入所得到的收益;y为监督管理者严格监管的概率,y∈[0,1]。
不进行安全投入的期望收益UB如式(2)所示:
(2)
式中:S为领导决策者进行安全投入的费用;E为对领导决策者的外部监管处罚;γ为事故发生率γ∈[0,1];B为发生事故后财产损失和声誉损失总和。
(3)
式中:x为领导决策者进行安全投入的概率,x∈[0,1]。
根据Malthusian动态方程[9]可知,策略的增长率等于该策略的相对适应性,设时间参数t,可得领导决策者在企业安全管理过程中选择进行安全投入策略的复制动态方程如式(4)所示:
(4)
同理对企业监督管理者,采取严格监管措施的期望收益ua如式(5)所示:
ua=G2x+(G2-s)(1-x)=G2-s+sx
(5)
式中:G2为监督管理者严格监管得到的收益;s为监督管理者可支配的安全项目款。
放松监管的期望收益ub如式(6)所示:
(6)
(7)
可得监督管理者在企业安全管理过程中选择严格监管策略的复制动态方程如式(8)所示:
(8)
由此可得复制动态方程的4个无条件均衡点O1(0,0),O2(0,1),O3(1,0),O4(1,1)。
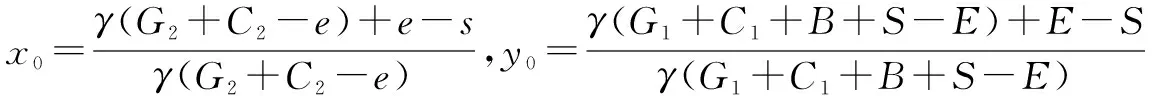
根据微分方程的稳定性定理可知,要使某一策略处于稳定状态,即演化稳定策略ESS[14],对于群体选择策略概率x和y需满足式(9):
(9)
2.1 领导决策者稳定性分析
由前文分析可得,当x=0,x=1并且y=y0时,根据稳定性定理,当F(x)=0,F′(x)≤0,x为ESS。
当y=y0时,对于所有的x,都可得F(x)=0,F′(x)=0,领导决策者的任何决策都是稳定策略。
当y≠y0时,进行如下分析:
1)E>S
γ(G1+C1+B+S-E)(1-y)+E-S>0,对方程的2个解x=0,x=1,可得F′(x)|x=0>0,F′(x)|x=1<0。因此,x=1是唯一的ESS,即有限理性的领导决策者选择进行安全投入。
2)E ①当S>γ(G1+C1+B+S-E)+E时,则γ(G1+C1+B+S-E)(1-y)+E-S<0,对方程的2个解x=0,x=1,可得F′(x)|x=0<0,F′(x)|x=1>0。因此,x=0是唯一的ESS,即有限理性的领导决策者选择不进行安全投入。 ②当S<γ(G1+C1+B+S-E)+E时,存在以下2种状况: 由前文分析可得,当y=0,y=1并且x=x0时,根据稳定性定理,当F(y)=0,F′(y)≤0,y为ESS。 当x=x0时,对于所有的y,都可得F(y)=0,F′(y)=0,监督管理者的任何决策都是稳定策略。 当x≠x0时,进行如下分析: 1)e>s 则有γ(G2+C2-e)(1-x)+e-s>0,对方程的2个解y=0,y=1,可得F′(y)|y=0>0,F′(y)|y=1<0。因此,可知y=1是唯一的ESS,即有限理性的监督管理者会选择严格监管策略。 2)e ①当s>γ(G2+C2-e)(1-x)+e时,则有γ(G2+C2-e)(1-x)+e-s<0,对于方程的2个解y=0,y=1,可得F′(y)|y=0<0,F′(y)|y=1>0。因此,可知y=0是唯一的ESS,即有限理性的监督管理者选择放松监管策略。 ②当s<γ(G2+C2-e)(1-x)+e时,存在2种情况: 根据Friedman[15]提出的观点,一个由微分方程系统描述的群体动态,其稳定策略可由雅可比矩阵的局部稳定性分析得出。此系统的雅可比矩阵如式(10): (10) 根据局部稳定分析法对5个均衡点进行稳定性分析,结果见表2。 由表2可知,领导决策者和监督管理者的博弈系统中存在4个局部稳定点:(0,0)(不进行安全投入,放松监管);(0,1)(不进行安全投入,严格监管);(1,0)(进行安全投入,放松监管);(1,1)(进行安全投入,严格监管)。 表2 局部稳定性分析结果Table 2 Results of local stability analysis 令: 以x-y坐标系画图表示领导决策者和监督管理者选择策略的动态演化趋势,共存在8种博弈类型,如图1所示。 根据图1(a)~(d)可知,存在4种特殊情况,博弈双方的行为决策并不受对方的影响和制约,仅取决于自己的获利与处罚。 根据图1(e),当S 图1 演化博弈相位图Fig.1 Phase diagram of evolutionary game 根据图1(g),当存在情况如:S<γ(G1+C1+B+S-E)+E,s 为更直观地体现本文关于煤矿安全管理中领导决策人员和监督管理人员的行为策略演化稳定性分析结果,以下对①:E>S,e ①G1=100,C1=80,G2=50,C2=40,B=10,E=40,S=30,e=10,s=15,γ=0.2。 ②G1=100,C1=80,G2=50,C2=40,B=10,E=25,S=35,e=10,s=15,γ=0.2。 本文绘制了不同情况下煤矿领导决策者和监督管理者的策略演化博弈图,如图2和图3所示。 图2 情形①下系统策略演化博弈Fig.2 Evolutionary game of system strategy under case 1 图3 情形②下系统策略演化博弈Fig.3 Evolutionary game of system strategy under case 2 1)图2中,图2(a)表示博弈双方决策随时间变化,由于高额处罚的存在,随时间变化领导决策者逐渐趋向于选择进行安全投入,而对于监督管理者,转移安全经费带来的利益大于承担的损失和处罚,因此,逐渐趋向于选择放松监管;图2(b)表示博弈双方决策相互影响演化,此博弈系统只存在1个均衡状态,最终收敛于(1,0),即领导决策者选择进行安全投入,监督管理者放松监管。 2)图3中,图3(a)表示博弈双方决策随时间变化,当领导决策者的进行安全投入的概率低于x′时,具有较高初始概率的监督管理者倾向于严格监管,反之,具有较低初始概率的监督管理者倾向于选择放松监管。而当领导监督者的进行安全投入概率高于x′时,具有较低初始概率的监督管理者越倾向于选择放松监管,反之,具有较高初始概率的监督管理者倾向于严格监管;图3(b)表示博弈双方决策相互影响演化,博弈系统收敛于2个稳定点(0,1)和(1,0),即稳定均衡策略有2个:领导决策者进行安全投入,监督管理者放松监管;领导决策者不进行安全投入,监督管理者严格监管。 1)安全投入对于领导决策者、监督管理者的安全监管策略选择具有显著影响。缺少专项安全投入经费或安全经费过少时,企业决策者和监督管理者往往都会选择不安全的生产策略。因此,企业应当设立安全专项经费并严格落实,将安全投入纳入企业考核指标,强调安全管理工作的重要性。 2)事故发生率、事故损失等因素对于博弈系统具有一定影响。事故发生频率与事故损失的严重程度越大,决策者和监督者越倾向于进行安全投入和严格监管。因此,可以将企业的不安全行为纳入社会信用体系,通过加大对企业声誉的影响力,从侧面引导企业进行安全管理工作,减少事故的发生。 3)当违规生产或是违规监管的处罚高于企业安全投入经费时,企业决策者会积极进行安全投入,监督管理者实施严格监管。因此,应当加强建设生产行业内外部监督机制。在企业内部,扩大安全监管队伍,鼓励员工自我监督、相互监督,实施动态奖惩机制;在外部,政府协同监管部门开展定期检查,提高检查标准,加大检查力度。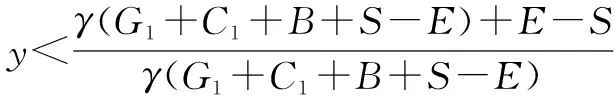
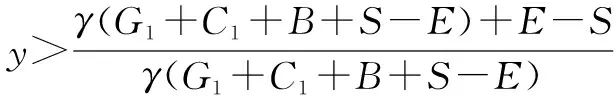
2.2 监督管理者稳定性分析
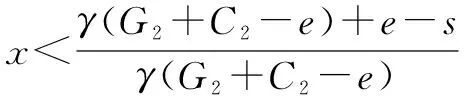
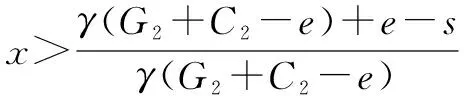
2.3 博弈双方间的ESS分析

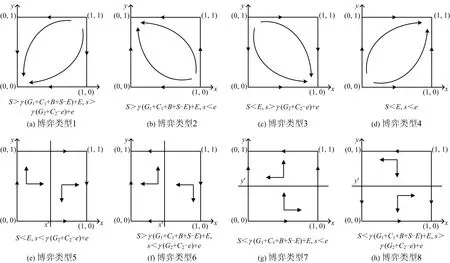
3 数值仿真模拟分析
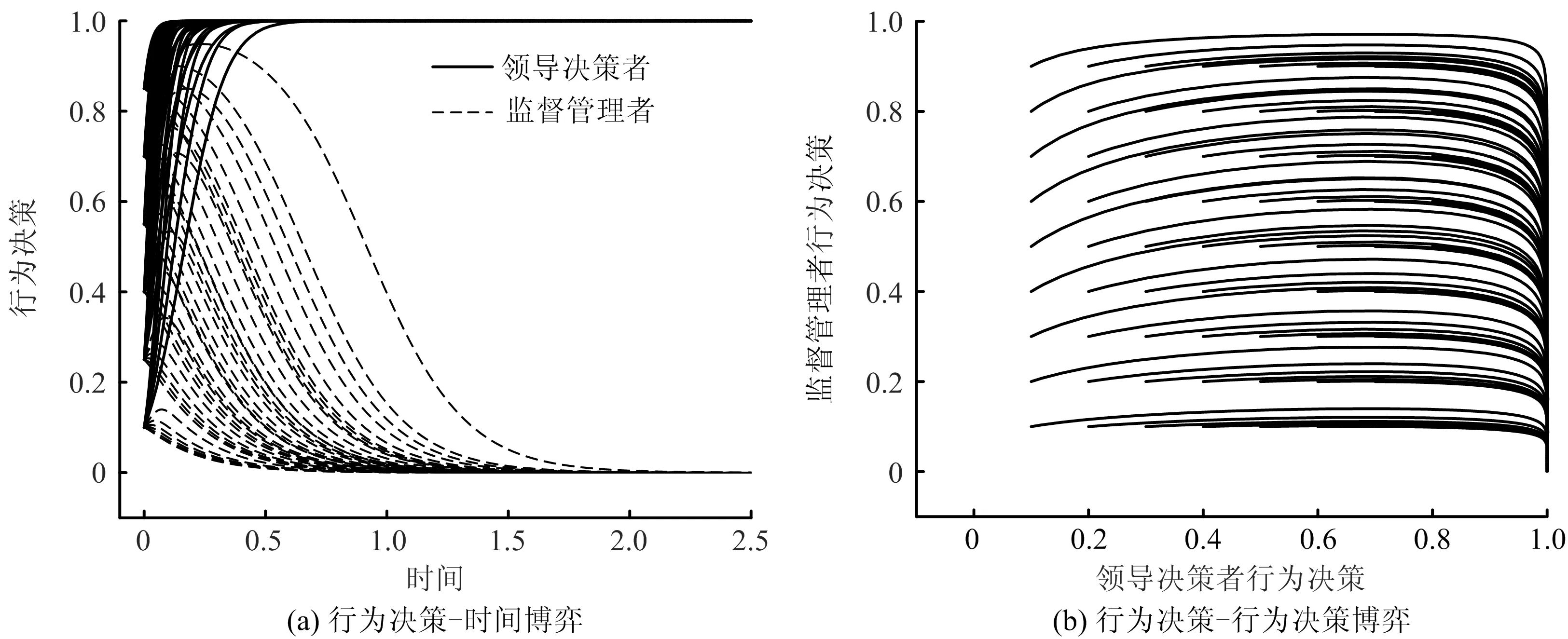
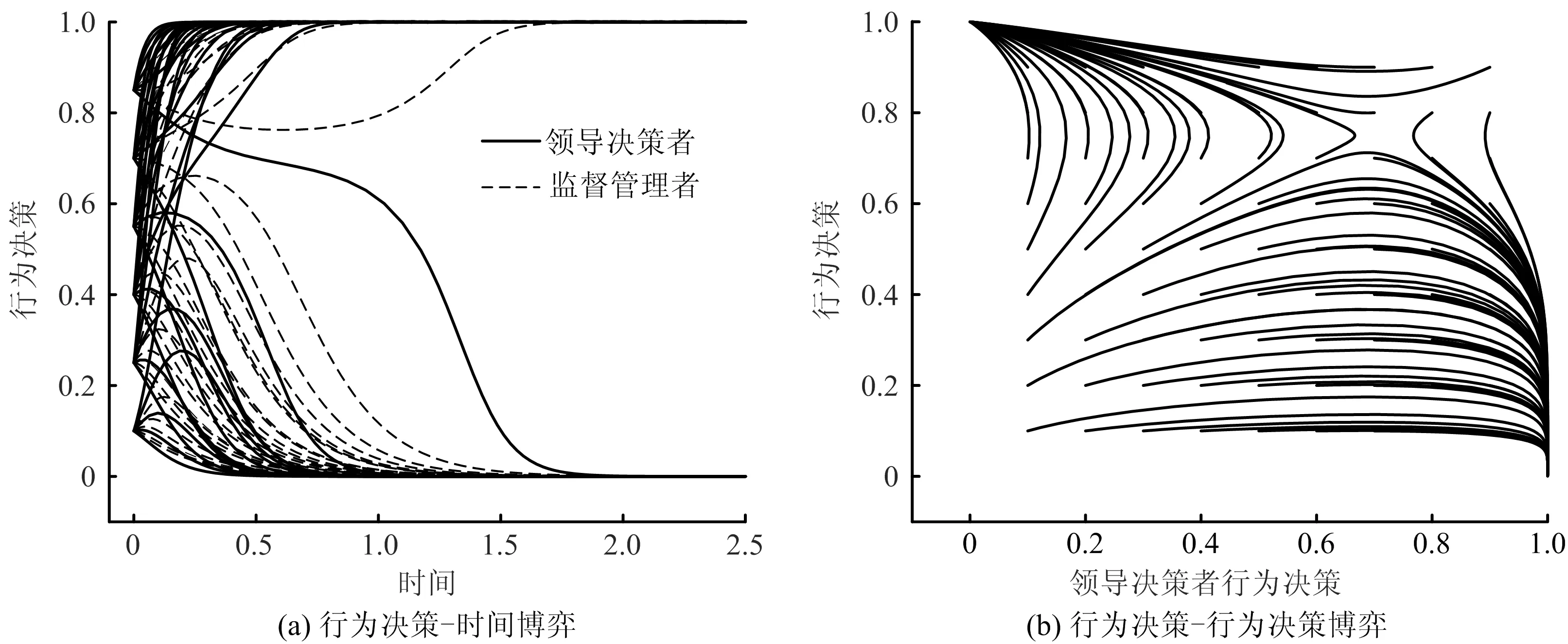
4 结论
