基于GPS钟差预测模型的列车定位技术研究
2022-04-26靳文军
郭 斐,靳文军
(中国铁路太原局集团有限公司侯马电务段,山西侯马 043000)
列车定位技术是列车运行控制系统的关键,高精度的列车位置信息在区间内安全运行至关重要。自动运行防护系统(Automatic Train Protection,ATP)通过采集GPS卫星定位提供的定位信息为列车正常运行提供安全评估策略。利用GPS定位方法实现列车完整性检查,为列车定位功能提供很好的技术参考,但是在实际的铁路应用中,列车运行环境复杂多变,安装在列车尾部的GPS接收机天线易受到运行环境的干扰,导致接收机的卫星信号不足而无法实现列车的精准定位。为解决上述问题,本文提出一种利用卫星钟差数据辅助实现列车GPS定位的方法,为列车安全运行提供信息保障。
1 灰色理论的钟差预测模型
灰色系统理论是关于信息不完备或不确定的控制理论,通过“部分”已知信息的生成、开发,实现对现实世界的确切描述和认知,能够通过对不完备信息建模来解决系统问题的算法,可以降低数据的随机性。所以通过灰色系统理论建立的钟差预测模型不需要对原始的钟差序列做出任何统计规律的假设。
将GPS接收机钟差序列的变化过程看做是一个灰色系统,对原始钟差序列Z=[Z(1),Z(2),…,Z(L)]建立模型。
对原始钟差序列进行一次累加,生成一个新的钟差序列Z(1),如公式(1)所示。

检验新钟差序列Z(1)的指数规律性,如公式(2)所示。

如果当t>3, 1<σ(t)<1.5时,则确定新钟差序列Z(1)具有指数规律。
对新钟差序列Z(1)建立微分方程式,如公式(3)所示。

依据最小二乘法的方法,估计a与u的参数,如公式(6)、(7)所示。

2 定位模型算法推导
2.1 定位模型建立
GPS伪距公式,如公式(9)所示。
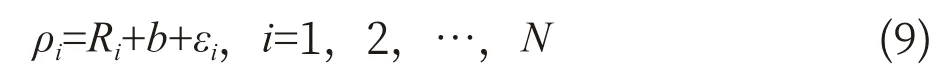
公式(9)中,ρ为伪距;Ri是第i颗卫星与GPS接收机之间的几何距离;b是GPS接收机天线与卫星的钟差;εi是系统误差。
将公式(9)用泰勒级数在接收机的概略坐标(x0,y0,z0)处展开,将其高次项忽略,便可得公式(10)的观测方程。

公 式(10)中,L∈RN×1是伪距差向 量;H∈RN×4是系数矩阵;X∈R4×1包含GPS接收概略坐标(x0,y0,z0)的改正数δx、δy、δz。
2.2 GPS接收机的定位算法推导
在列车运行过程中,GPS接收机天线持续不断的接收卫星信号,t时刻,列车GPS接收机天线受外界环境干扰,接收到GPS卫星信号不完备时,在上述观测方程中引入预测钟差值,并通过扩充观测矩阵的方式实现对列车的GPS的精准定位。
首先,将实际的钟差值b用预测得到的钟差值B代替,得到系统方程,如公式(11)所示。

公式(11)中,L'∈RN×1为扩展后的伪距差向量;H'∈RN×3为扩展后的系数矩阵;X'∈R3×1包含了列尾GPS接收机的概略坐标(x0,y0,z0)的改正数δx、δy、δz。

公式(12)中,l1、m1、n1为列尾GPS接收机与第i颗卫星之间的方向余弦,其中如公式(13)所示。
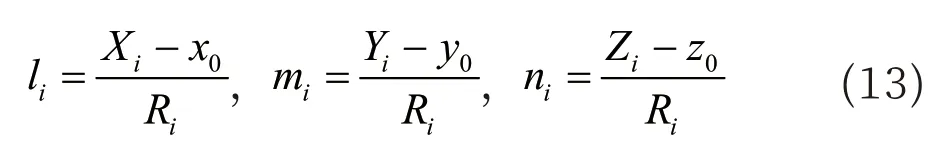
公式(13)中,(x0,y0,z0),(Xi,Yi,Zi)分别为t时刻GPS接收机的坐标和第i颗卫星的坐标。
由上述公式可以看出,建立钟差预测模型后,原来的4个未知参数变成3个。所以,在接收卫星信号不完备条件下,通过钟差模型辅助的方法可以实现对列车GPS接收机的定位。
3 定位验证
本文在静态情况下对钟差预测模型辅助的GPS定位方法进行验证。
3.1 实验条件
利用GPS接收机采集卫星定位数据:持续5 min,采样间隔为1 s,共收集定位数据300组。首先将前4 min所采集到的钟差数据进行提取,并建立钟差预测模型。通过建立的钟差预测模型对第5 min的钟差值进行预测,将预测值代入观测方程辅助完成列车GPS定位。如图1所示。

图1 实验所需钟差采集数据Fig.1 Samples of clock bias for the experiment
3.2 预测验证
由于GPS接收机的实际钟差数据较大,通过这些数据直接来建立钟差预测模型,最终的运算量必然会很大,对列车的定位计算造成一定的困难。所以先对该钟差序列进行了一次差分运算,然后再对差分运算得到新的钟差序列建立灰色预测模型,从而降低运算量。另外,在建立模型之前,还需要验证钟差序列的指数型规律,评价指标σ(t)。如图2所示。
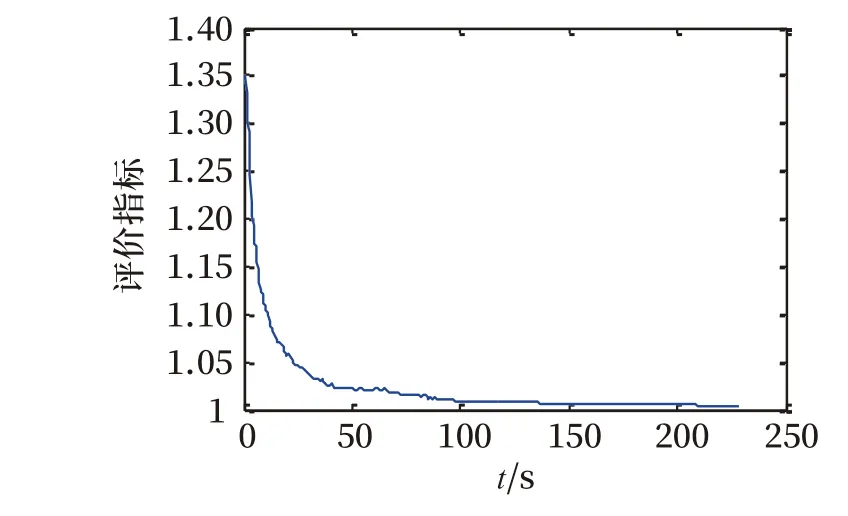
图2 钟差序列指数规律Fig.2 Exponential pattern of clock bias sequence
由图2可知,当1<σ(t)<1.35时,钟差序列满足指数规律,可以对其建立灰色模型。
如图3所示,钟差预测误差的值随时间而增大。其平均误差为14.47 m,但是在240~250 s之间,预测值变化较小,也就是说,模型在短时间内进行预测,可以较好的反应出钟差序列的变化趋势。因此,基于灰色理论的GPS接收机钟差预测模型能够适用于短期钟差预测。
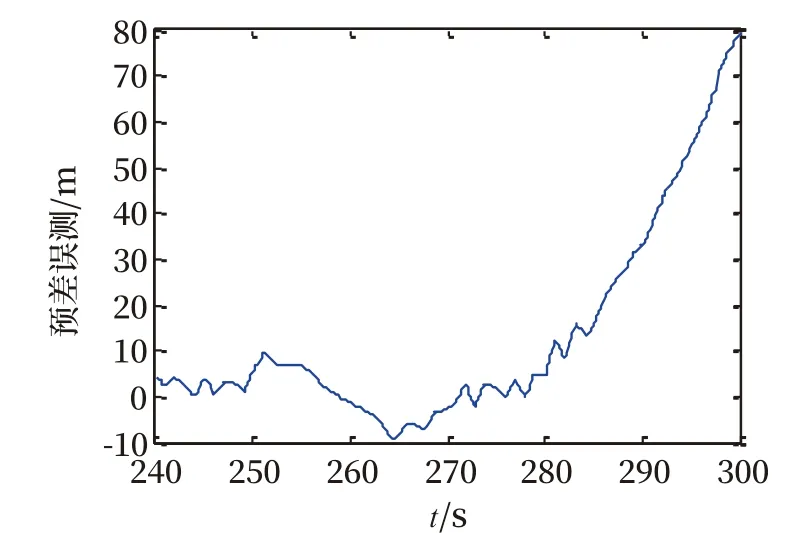
图3 钟差预测误差Fig.3 Errors in clock bias prediction
3.3 定位实现
通过上述模型来辅助GPS接收机以实现最终的坐标定位。
通过引入钟差预测模型解算的列车GPS定位,具有较高的精确度。如图4所示,在240~270 s之间,定位误差在20 m以内,该精度可以满足列车在短时间的定位要求。当时间超过300 s,误差也将超过75 m,定位解算误差稍大,仅具有一定的参考价值,不适用于列车安全运行的信息保障。
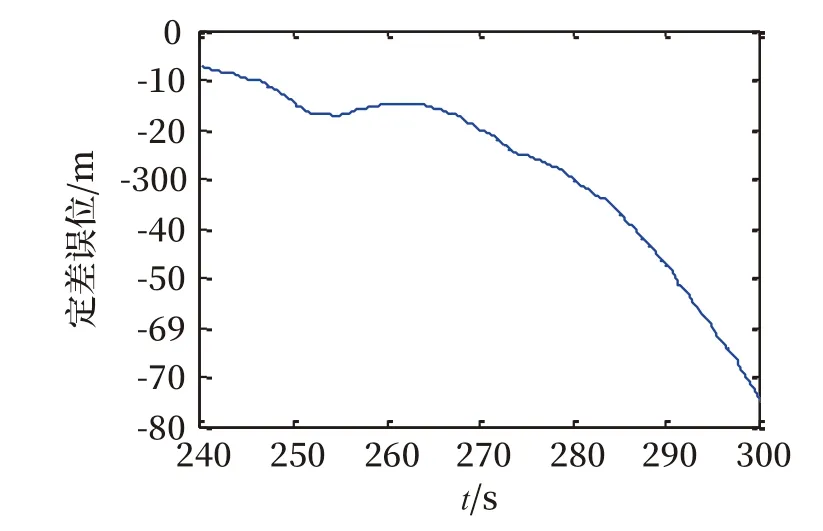
图4 X轴方向的定位误差Fig.4 Positioning errors in X-axis direction
4 结束语
本文根据列车实际运行状态下,GPS接收机在无法使用常规4星定位情况下,提出了一种新的GPS定位列车的解算方法,即将GPS接收机的钟差序列的变化过程看做是一个灰色系统,建立钟差预测模型,从而实现列车的GPS定位解算。验证结果表明,该方法具有较高的定位精度,能够满足列车在复杂环境下的GPS定位要求。
