毫米波MIMO的DNN混合预编码梯度优化方法

王 勇，王喜媛，任泽洋

(1.西安电子科技大学 网络与信息安全学院，陕西 西安 710071；2.西安电子科技大学 信息科学研究中心，陕西 西安 710071；3.北京邮电大学 国际学院，北京 100876)

在超高频段(如毫米波)中如何使用大量未充分利用的频谱，最近引起了研究界的极大兴趣。毫米波系统的频谱效率的最大化可近似归结为全数字预编码器和混合预编码器之间欧氏距离的最小化问题。AYACH等[1]将其转化为稀疏重建问题，并通过正交匹配追踪(OMP)算法加以解决。然而，这种对可行模拟预编码求解方案空间的限制导致了频谱效率的降低。YU等[2]提出了另一种交替最小化算法(AlgMin)，该算法基于流形优化技术，将模拟预编码器上的单位模成分嵌入复平面上多个圆的乘积中。尽管该算法提供了接近最优的频谱效率，但由于其在数字基带预编码器和模拟预编码器之间存在嵌套环路结构，不仅会减慢程序的收敛速度，而且由于克罗内克乘积，处理大型矩阵的复杂性极高。在文献[3]中，提出了一种基于连续干扰消除的混合预编码方法，该方法能够以较低的复杂度实现优异的性能，其中将具有非凸约束的和速率优化问题分解为若干个子速率优化问题。此后，ALKHATEEB[4]通过配置混合预编码器设计了一种用于多用户毫米波系统的低复杂度混合模拟/数字预编码。然而，由于过去提出的混合模拟/数字预编码方案是基于奇异值分解(SVD)的，因此在先前的工作中提出的这些预编码方案具有较高的计算复杂度，并且需要复杂的比特分配策略，得到用户的各子信道的等效信道增益差异化被放大，导致不同数据流的信噪比不同。此外，新提出的基于几何平均分解(GMD)的方案可以避免比特分配问题，但它在解决模拟预编码器的非凸约束和利用毫米波大规模多输入多输出系统的结构特性方面仍然带来了巨大的挑战。

尽管已经有大量的研究致力于提高混合预编码频谱效率，但仍然存在许多问题，例如基于几何平均分解的方案[5]，基于矩阵分解的混合预编码平均值方法[6]，基于射频的预编码方法以及基带信号处理和混合空间处理架构辅助预编码方法[7-8]等。此外，为了实现高频谱效率和低复杂度，提出了一种交替最小化方案，用于有效地设计混合预编码器[2]，并利用压缩感知检测器处理低维波束空间信道状态信息。由于传统方法没有充分利用毫米波多输入多输出系统的结构特征和稀疏统计特性，因此传统方法实现低复杂度的代价是降低系统的混合预编码性能。以往的工作未能从根本上解决这些问题，迫切需要提出新的方法来提高毫米波大规模多输入多输出的混合预编码性能。

最近几年，被称为深度学习[9]的新兴解决方案是一种处理海量数据和解决复杂非线性问题的优秀技术。事实证明，深度学习是处理复杂非凸问题和高计算量问题的优秀工具，其卓越的识别和表示能力决定了深度学习的优越性。将深度学习融入通信的一些前期工作，主要包括波束选择、非正交多址(NOMA)、大规模多输入多输出和异构网络[10-13]。文献[14]还研究了太赫兹通信中的混合预编码，其中部署了超大规模天线以克服巨大的传播损耗。随后，提出了一种动态子阵混合预编码方案，以平衡频谱效率和功耗。

针对上述问题，笔者引入了深度神经网络(DNN)的训练来选择混合预编码器。结合基于块对角化的几何平均分解，采用改进的梯度计算算法和单循环迭代结构，将预编码器的优化选择视为深度神经网络中的映射，以优化大规模多输入多输出的混合预编码过程。实验结果表明，与其他方案相比，笔者提出的混合预编码优化方案，当频谱效率为50 bit/(s·Hz)时，可节省信噪比 3 dB。若不同方案达到相同误码率，则可节省信噪比 5 dB以上，并具有更好的稳健性。

1 系统模型

x=VAVDs=Vs，

(1)

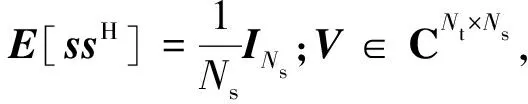
(2)

2 基于深度学习的GMD混合预编码优化设计

2.1 基于块对角化的几何均值分解

前期的研究发现，ZF预编码算法和BD预编码算法是将多输入多输出信道分解为平行的子信道，用户的各子信道的等效信道增益并不相同，导致不同数据流的信噪比不同，从而引起误码率的不同。而系统总误码率是由最差子信道来决定的。为了消除这种子信道之间信噪比差异导致部分子信道误码率较高进而影响整体误码率的情况，笔者使用基于块对角化的几何均值分解(GMD)[15]。

由于毫米波大规模多输入多输出信道中的有限散射，H具有低秩特性，可以利用有限数量的射频链路实现接近最佳吞吐量。频谱效率的最大化问题近似归结为全数字预编码器和混合预编码器之间的欧氏距离的最小化问题，该问题可进一步表述为全数字预编码器的矩阵分解问题，即优化数字基带预编码器矩阵和模拟射频预编码器矩阵的乘积。

H的块对角化几何均值分解可表示为

(3)

其中，W1∈CNr×Ns，为半酉矩阵，表示发射预编码矩阵；V1∈CNt×Ns，为半酉矩阵，表示接收合成矩阵。另外，Q1∈CNs×Ns，是对角线元素相等的上三角矩阵，对角线元素表示H特征值的几何均值，因此可获得增益相等的子信道。接收机获得的接收信号可表示为

(4)

优化目标可以直观地理解为：最优混合预编码器将无限逼近于无约束最优全数字预编码器。用Vopt表示最优全数字预编码器矩阵，因此优化目标可表示为

(5)

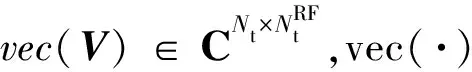
(6)

(7)

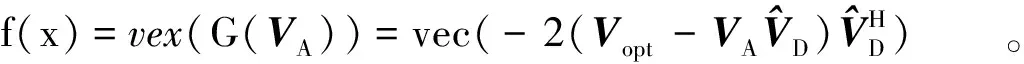
(8)

2.2 深度神经网络优化学习

深度神经网络是深度学习框架中最普遍的结构，可以看成是多层感知器。具体而言，与传统的神经网络相比，深度神经网络中任何存在的隐藏层都以增强其学习和映射能力为目标。在深度神经网络中，许多单元部署在各个隐藏层中，并且基于这些单元的输出借助激活函数生成最终的输出。在本文中，非线性运算中使用了校正线性单元(ReLU)函数。

为了实现混合预编码，笔者构建了一个两阶段深度神经网络框架，如图1所示。在输入层中，每个训练序列的长度由其维度决定，是一个具有128个单元的完全连接层，用于捕获输入数据的特征。用于处理编码操作的两个隐藏层也是完全连接层，分别包含400个单元和256个单元。接下来，为了用AWGN噪声加扰，需要一个由200个单元组成的噪声层，用于混合失真。随后，为了实现解码，笔者设计了另外两个隐藏层，分别具有128个单元和64个单元。最后，部署输出层以生成网络的预期输出信号ReLU函数，作为输入层和隐藏层的激活函数引入深度神经网络。

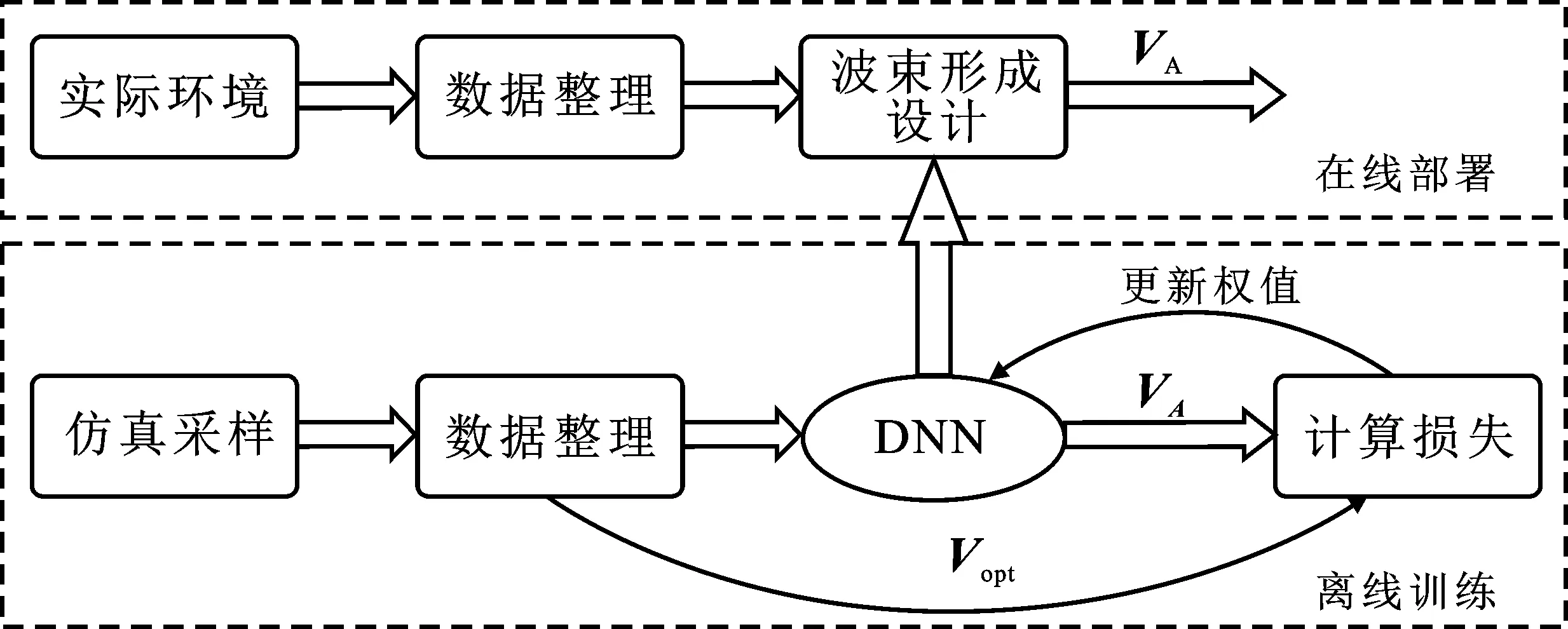
图1 两阶段深度神经网络框架

根据式(8)可知，x处的黎曼梯度通过将∇f(x)向切空间TxOB(m，C)投影获得，即

f(x)=Px∇f(x)=ξ，

(9)

其中，Px表示向TxOB(m，C)空间的投影算子；ξ∈TxOB(m，C)，表示f(x)的梯度下降方向。最终第k次迭代数据更新为

xk+1=Rxk(-αkξk) ，

(10)

基于深度神经网络的学习过程如下。

目标：获取最优预编码器Vopt。

① 初始化：迭代次数k=0，误差门限τ=10-7，任意选取初始x0；

② 产生训练数据集；

植物园中的盆栽桂花、银边翠、时令蔬菜，质量分数为4.2%的碳酸氢钠溶液、质量分数为25%的氢氧化钠溶液、质量分数为0.1%的碘液。

③ 构建紧度神经网络

④ while( error ≥τ)

⑥ 根据式(8)计算欧氏梯度∇f(xk)；

⑦ 根据式(9)计算黎曼梯度ξk；

⑧ 根据式(10)更新xk+1；

⑨ 从网络的输出层获取xk+1和xk的偏差；

从上述整个迭代过程，可以得到

(11)

2.3 计算复杂度分析

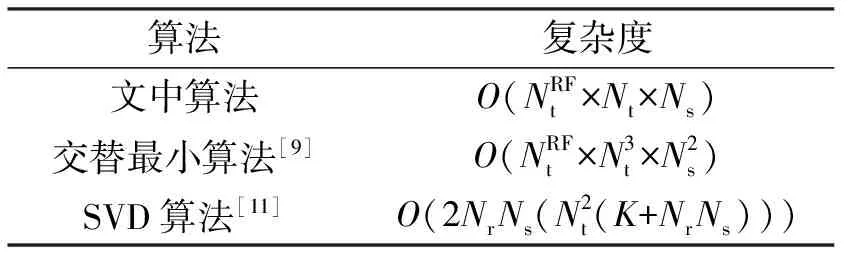
表1 不同预编码方案计算复杂度对比

3 算法仿真与分析

图2展示了基于深度神经网络的混合预编码方案、交替最小化算法[9]和奇异值分解方案[11]相对于信噪比的频谱效率。从图2中可以看到，所有方案中频谱效率随着信噪比的增加而提高。此外，从图2还可以看出，所提出的混合预编码方案优于其他策略，其通过深度学习的映射和学习能力实现了更好的混合预编码性能。此外，随着信噪比不断增加，基于深度学习方案的性能优势相对于其他算法愈加明显，更趋近于最优的全数字预编码，这进一步证明了所提出的混合预编码方案的有效性。

图2 不同方案下频谱效率对比

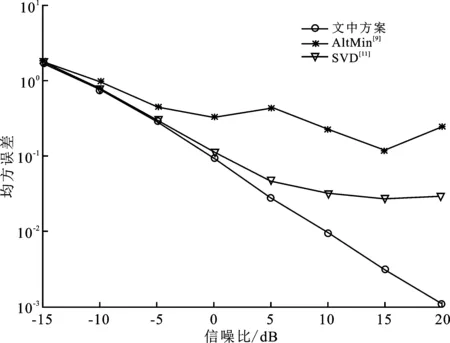
图3 不同方案下均方误差对比

图4 不同方案下误码率性能对比

为了研究混合预编码方法的鲁棒性和稳定性，引入均方误差(MSE)，即EMSE=E‖Vopt-VAVD‖2，探索基于深度学习策略与不同混合预编码方案之间的关系。如图3所示，所提出的基于深度学习的方案的均方误差性能优于其他方案，可知笔者提出的基于深度学习的方法与其他方案相比，在混合预编码精度方面性能优异。

如图4所示，因为几何平均分解方案对反馈误差较为敏感，当信噪比较低时，分层检测有误差传播效应。但是，当信噪比足够好时，奇异值分解算法得到用户的各子信道的等效信道增益差异化被放大，而基于块对角化的几何平均分解方案的误码率性能优于其他方案。基于深度学习策略与传统方法相比，由深度学习的优化能力导致性能改善更为明显。此外，由于深度神经网络利用了结构化信息，可以逼近混合预编码算法的每次迭代，验证了所提出的混合预编码策略优于基于AlgMin和奇异值分解的方案，这意味着可以借助深度学习解决混合预编码中存在的非凸优化问题。

4 结束语

笔者提出了一种基于毫米波系统混合预编码器设计的快速优化算法，可以显著地降低计算复杂度，并充分利用毫米波大规模多输入多输出场景中大型天线系统的空间统计特性。通过设计基于深度学习的混合预编码方法，分析和验证了基于深度神经网络方法的性能。利用实验仿真和现有方案比较可知，笔者提出的深度神经网络下快速优化算法具有很强的识别和映射能力，有利于混合预编码的快速收敛和性能提升。