基于准Karhunen-Loève 变换基的字典学习抗距离假目标干扰方法

于乐新，张慧，龚琳舒，姜弢*

1 哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001

2 上海机电工程研究所，上海 201109

0 引 言

舰载雷达是一种对海面或空中目标进行定位和跟踪的探测设备，是敌方干扰的重点对象[1-2]。近年来，电子对抗技术随着舰载雷达的发展而日臻成熟，其中最具特色的是发展迅猛的数字射频存储器（digital radio frequency memory, DRFM）技术，其为干扰方法提供了有效支撑[3]。由于DRFM技术形成的欺骗式干扰信号是一种与雷达发射信号具有很强相干性的信号，雷达系统难以正确获取目标物体的距离或速度信息，使得这种欺骗干扰成为舰载雷达的最大威胁[4]。

为此，在国外，Soumekh[5]首次将波形分集技术引入到了雷达抗干扰领域，通过在不同脉冲重复频率中的线性调频（linear frequency modulation,LFM）信号进行相位扰动或调频斜率变化，利用匹配滤波限幅处理达到欺骗干扰抑制的目的。以波形分集技术为基础，Akhtar[6]提出了一种正交脉冲块编码的方法用来对抗有源欺骗干扰。该方法设计了4 个具有特定结构的正交编码信号在脉冲重复间隔（pulse repeat interval，PRI）时间内连续发射，通过匹配滤波造成干扰信号失配，从而实现干扰抑制的目的。在国内，卢术平[7]提出基于雷达环境知识库中电子干扰先验知识的波形设计算法来实现对抗新体制干扰。近年来，随着波形分集技术的发展，又不断出现了脉间频率捷变信号、编码信号、时变的正交频分线性调频（orthogonal frequency division LFM，OFD-LFM）信号、基于混沌序列的雷达正交信号等雷达波形用于抗干扰研究[8-11]。然而，在强能量干扰条件下，干扰信号经过匹配滤波器而产生的失配会形成较高的距离旁瓣干扰。因此，上述文献中采用的技术方法在大功率干扰环境下无法保证雷达系统正常检测到真实目标。

本文将以波形分集技术为基础，采用捷变相位扰动线性调频（phase perturbation LFM, PPLFM）信号作为雷达系统发射波形，研究提出基于非齐次 线 性 均 方 估 计（non-homogeneous linear mean square estimation, NLMSE）模板[12]匹配准Karhunen-Loève 变换（quasi-Karhunen-Loève transform ，Q-KLT）基的抗距离假目标干扰方法，以解决强能量干扰下的雷达抗DRFM 欺骗式干扰问题。基本思路如下：首先，在一个距离波门内，利用含有距离维信息的雷达信号相关函数构造目标和干扰的初始化字典；然后，从字典中选取与雷达回波自相关矩阵对角向量之间具有最大相关系数的原子，将其原子与初始化字典生成自相关矩阵模板，采用NLMSE 方法求取各模板的线性组合系数，即计算出匹配系数；再通过计算模板与匹配系数构成目标和干扰的近似自相关矩阵，对其自相关矩阵进行特征值分解，分别得到目标和干扰对应的近似Q-KLT 基；最后，采用凸优化算法（convex optimization algorithnm）实现目标和干扰信号的分离，达到抑制大功率距离假目标干扰和距离旁瓣干扰的目的。

1 信号模型

PPLFM 波形是雷达在一个相干处理间隔（coherent process internal，CPI）时间内发射N个受到不同相位扰动的脉冲信号，其中第n个PRI 时间内发射的信号表示为

式中：k=B/T，为LFM 信号的调频斜率（其中B为信号带宽，T为信号时宽）；t为时间； θn(t)为随机信号，即表示为

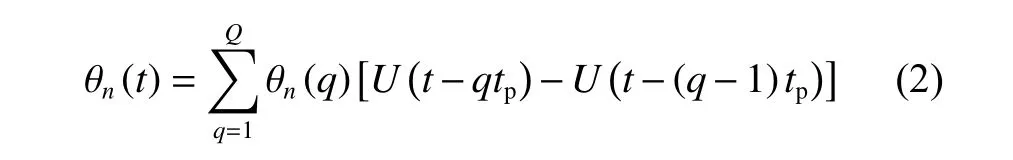
其中，信号被分为Q=T/tp个 子脉冲（tp为子脉冲的时 宽），U(t) 为 阶 跃 函 数， θn(q)为 第n个PPLFM信号第q个子脉冲相位编码（ θn(q)∈[-π,π]）。

雷达接收信号经匹配滤波处理后的输出为

式中：An(t)=Sn(t)⊗Sn(t)，为第n个PRI内的PPLFM信 号Sn(t) 自 相 关 函 数；Cn(t)=Sn(t)⊗J(t)，为第n个PRI 内的PPLFM 信号与干扰信号J(t)之间的互相关函数； σT和 σJ分别为目标和干扰信号的幅度； τT和 τJ分 别为目标和干扰的时延；Wn(t)为高斯噪声信号。

2 字典学习抗干扰方法

估计干扰信号滞后雷达发射信号的周期个数，采用干扰信号滞后周期个数作为抗干扰方法的先验信息。估计周期个数的方法是尖峰检测，其基本原理是根据目标回波与干扰信号在脉间初相捷变波形的相位方面上存在的差异性，采用小波变换估计相邻周期信号压缩尖峰的相位差，进而判断滞后的周期个数。工作流程如图1 所示。尖峰检测的具体步骤如下：

图1 尖峰检测法估计干扰滞后周期个数的工作流程图Fig. 1 Flow chart of estimating the number of jamming lag periods using spike detection method

雷达端在CPI 内发射一种特定的脉间初相捷变波形，第1 个捷变波形的初相设置为φ1=φ（ φ为参数），其他波形的初相都为φn=0。假定干扰滞后周期个数为3，则干扰机发出的捷变波形的初相为φ4=φ；其后，第1 个波形和第4 个波形脉冲压缩处理后的相位残差分别为 θ1=φ和 θ4=-φ；最后，估计第1 个脉压信号尖峰依次与后面N-1个脉压信号尖峰的相位差，在第3 次检测估计出的 相 位 差 为 θˆ1,4=2φ，而 其 他 估 计 的 相 位 差 为θˆ1,n=φ (n≠4)，最终，确定干扰机发出的干扰信号滞后发射信号的周期个数等于3。

根据以上方法获取到干扰信号滞后的周期个数，同时确定出干扰信号中的相位编码序列，从而构建出目标与干扰的初始化字典Di(i=1,2)，

式中： τp=2(dmin+p·d)/C，为信号时延，其中d表示最小分辨距离，雷达距离波门宽度范围是 [dmin,dmax]，C表示光速；P=(dmax-dmin)/d，为可确定的初始化字典中原子数目。

将初始化字典Di(i=1,2)中的原子转化成自相关矩阵对角向量，形成字典Gi(i=1,2)，生成自相关矩阵模板以及计算求得匹配系数，并构建目标和干扰信号的近似Q-KLT 基，再采用基追踪（basis pursuit，BP）算法[13]实现目标与干扰的分离重构，达到抑制距离假目标干扰的目的。

基于Q-KLT 基抗距离假目标干扰方法的具体步骤说明如下：

1） 计算雷达接收信号y的自相关矩阵Ry和对角向量dRy。雷达接收信号y经离散傅里叶变换（DFT）得到信号Y，计算接收信号的自相关矩阵：

对角向量为

2） 从字典Gi(i=1,2)中 选取与对角向量dRy的

相关系数最大的P个原子，g,g,···,g（其中，k为字典G中原子g的标号，m为原子g的个数）。

4） 采用NLMSE 方法计算模板的匹配系数a,a,a,···,a，使得式（7）最小化。

7）最后，将目标和干扰信号的近似Q-KLT基构成联合字典U=[U,U]，采用BP 算法求解下面的凸优化问题得到其最优解，即实现目标与干扰信号的分离。稀疏估计值为

式中:a为联合字典U下的稀疏系数；ε 为最小边界值。

3 模拟仿真

为了验证抗距离假目标干扰方法的有效性与优越性，本文利用Matlab 对算法进行了仿真。设置LFM 信号带宽B=10 MHz，信号时宽T=10 μs，脉冲重复间隔时间PRI=200 μs，相位编码序列的码 长 为100。设 置 干 信 比JSR=20 dB，信 噪比SNR=10 dB。假定目标回波时延为125 μs，干扰信号时延分别为126，126.5 和127 μs。

首先，利用遗传算法（GA）优化设计出具有较低自相关旁瓣的PPLFM 信号，进一步降低距离旁瓣干扰。然后，在单个假目标和多个假目标干扰的环境下，采用基于NLMSE 模板匹配Q-KLT 基的抗距离假目标干扰方法，实现目标和干扰信号的分离。

图2（a）和图2（c）为固定LFM 信号通过匹配滤波器输出的信号，干扰信号的增益幅度远高于目标回波，使得雷达系统无法甄别出正确目标的距离信息。图2（b）和图2（d）为优化设计后的PPLFM 信号结合字典学习抗干扰方法，此方法可以有效分离出强能量的干扰信号，从而达到抑制距离假目标干扰并获得真实目标信号的目的。

图2 干扰抑制仿真结果Fig. 2 Simulation results of jamming suppression

图3 给出了100 次蒙特卡洛仿真结果。由图可见，干扰信号投影向量的Gini 系数[14]随着JSR的增大而提高；目标信号的Gini 系数随着JSR的增加先增大后减小，且在1 个假目标场景下的目标投影向量稀疏性要好于3 个假目标场景下的稀疏性。

图4 给出了100 次蒙特卡洛仿真得到的干扰抑制后PSLR值随JSR的变化曲线，由图可见，峰值旁瓣比（peak side lobe ratio，PSLR) 值呈现出了先升后降的变化趋势，其与图3所示的目标信号投影向量的Gini 系数变化曲线几乎相同。

图3 Gini 系数随着JSR 变化曲线Fig. 3 The Gini coefficient varying with JSR

图4 干扰抑制后的PSLR 值随着JSR 变化曲线Fig. 4 The PSLR value after jamming suppression varying with JSR

对比图3 与图4 可以发现，在JSR较低且干扰和目标投影向量稀疏性较低时，对抗距离假目标干扰的性能也会较差（PSLR值较低）。在JSR提高后，干扰和目标投影向量的稀疏性得到提升，抗干扰性能也随之增强，进一步提高JSR后，干扰投影向量的稀疏性仍然提升，目标投影向量的稀疏性在下降，从而抗干扰性能也会变弱，但其性能优于低JSR条件下的抗干扰性能。从中可以看出，信号在自适应字典（基函数）下所具有的良好稀疏性可实现干扰与目标信号的完美分离，使得干扰抑制后的PSLR值相当于目标信号本身（无干扰影响）经过匹配滤波后的PSLR值，进而意味着本文方法的抗干扰性能会受到信号在Q-KLT基下稀疏性的影响。而在1 个假目标场景下干扰抑制后的PSLR值高于在3 个假目标场景下的PSLR值。当JSR=30 dB 时，PSLR值 依 然 可 以 达到15 dB 以上，进一步显示了本文所提出方法抑制大功率的距离假目标干扰的优越性。

4 结 语

针对舰载雷达系统在复杂电磁环境下受到转发式大功率欺骗干扰威胁的问题，本文以波形分集技术为基础，研究了一种用于对抗大功率距离假目标干扰的基于Q-KLT 基的字典学习方法。通过仿真，以Gini 系数和PSLR值为指标，分别衡量了所提方法在典型JSR条件下的稀疏性和抗干扰性能。仿真结果显示，PSLR值的变化趋势与目标信号投影向量的Gini 系数变化曲线几乎相同，说明目标信号在Q-KLT 基下的稀疏性表征了所提方法的良好抗干扰性能。当JSR=30 dB 时，干扰抑制后的PSLR值仍保持在15 dB 以上，这明确说明了该方法在强能量干扰环境下的优越性。