复杂加筋的锥-柱组合壳声振相似规律研究

彭才赓，张诗洋，张冠军*

1 武汉理工大学 高性能船舶技术教育部重点实验室，湖北 武汉 430063

3 武汉理工大学 能源与动力工程学院，湖北 武汉 430063

3 中国舰船研究设计中心，湖北 武汉 430064

0 引 言

随着声呐探测技术的发展，声隐身性能直接影响潜艇的作战能力和生命力，而振动噪声（以下简称“声振”）水平直接影响声隐身性能，是潜艇设计的关键性能指标之一[1]。潜艇在使用过程中需要长时间在水下活动，过高的声振水平不仅直接影响艇员的身心健康，还会对海洋生态环境造成一定破坏，故声振控制也是潜艇设计研究的重要内容。然而，潜艇实艇的声振试验给研究工作带来了诸多不便，例如实艇尺寸较大、试验成本高、试验周期长、难度大等，国内外学者更倾向于通过缩尺模型来开展相关试验，即将从缩尺模型获得的数据换算到实艇上。因此，关于缩尺模型的相似规律的研究显得尤为必要。目前，在壳体声振相似领域已取得了一些研究成果，但对于相对复杂的组合壳结构（例如结构较复杂的实艇），采用缩尺模型的声振试验结果仍难以准确预报原型的声振特性。

对于结构声振相似性问题，国内外学者开展了部分研究。例如：李瀚钦等[2]以加筋圆柱壳为对象，分析了不同相似条件对结构声振相似性的影响，对水下结构振动与声辐射相似机理进行了研究总结。Coutinho 等[3]总结了结构工程领域的相似理论（包括基于量纲分析法、微分方程法和能量法等的理论），为结构相似理论研究提供了支撑。Balawi[4]通过有限元分析（FEA）与试验测试相结合的方法，研究了壳体的振动相似比，结果表明，采用有限元法（FEM）研究壳体振动相似规律是可行的。俞孟萨等[5]研究了水下弹性结构体的耦合声振响应的相似性，采用有限元-边界元法（FEM-BEM）混合方法建立了弹性体结构水下振动方程，推导出了水下声振特性相似比，并结合试验验证了相似理论的准确性。白长玉[6]在总结不同相似分析方法的基础上，通过量纲分析法进行了相似理论的推导，进而采用有限元仿真计算验证了结构的振动相似性。Petrone 等[7]在完全相似的加筋圆柱壳基础上，采用FEM 研究了结构畸变时的振动相似性，结果表明，在考虑畸变结构时也可取得较好的预测结果。此外，施傲等[8]基于试验相似原理，采用量纲分析法得出了完全相似结构模型的模态与振动响应的相似比，荣吉利等[9]通过量纲分析法建立了结构缩尺模型的相似比，并采用FEM 进行计算验证，为缩尺结构的声振预测和试验提供了理论依据。

综上所述，在壳体声振相似性研究领域，现有研究主要集中于相对简单的壳体结构，并对圆柱壳或圆锥壳展开了相似性分析。而对于更复杂的结构（例如加筋组合壳）在流体耦合作用下的相似性研究并不充分。鉴此，本文将采用面单元模拟加筋方法构建复杂加筋锥-柱组合壳结构及其缩尺模型，基于ANSYS 构建的模型，计算空气中的结构模态和振动响应，再将有限元模型和模态数据导入Virtual.Lab Acoustics 声学计算软件中，采用BEM 计算水下耦合模态及振动响应。最后，通过模型试验，验证采用FEM-BEM 混合方法计算复杂组合壳结构振动响应的准确性，以及复杂组合壳结构的水下声辐射效率和声指向性，研究复杂组合壳结构声振相似规律。

1 复杂加筋锥-柱组合壳模型建立

为了研究复杂加筋锥-柱组合壳声振相似规律，构建了如图1 所示的复杂加筋锥-柱组合壳结构模型，以及壳体、横舱壁、纵筋腹板、环肋腹板的几何模型。该组合壳模型以锥壳小端圆心为原点，轴向为x向，垂向为y向，水平向为z向。原型组合壳的参数如下：壳体结构长12 m（锥壳部分长8 m，柱壳部分长4 m），柱壳半径3.5 m，外壳厚0.04 m，锥壳小端半径1 m，大端半径3.5 m；锥壳上环肋高0.4 m，尾轴承支撑环半径0.7 m，内部横舱壁及纵筋腹板厚度为0.025 m；柱壳中环肋高0.4 m，纵 筋 高0.5 m，环 肋 均 匀 分 布，间 距0.5 m。1:4 的缩尺模型与原型完全相似。

图1 加筋锥-柱组合壳几何结构及有限元模型Fig. 1 Geometric structure and finite element model of stiffened cone-cylinder combined shells

壳 体 材 料 属 性 如 下：杨 氏 模 量 2.1×1011N/m2，泊松比0.3，密度7 800 kg/m3，阻尼比0.003。在构建的有限元模型中，锥-柱壳体部分和环肋及纵筋的腹板均采用SHELL 181 面单元模拟，环肋和纵筋面板采用BEAM 188 梁单元模拟。根据壳体振动弯曲波的波长理论（即一个波长范围内有6 个单元），计算有限元模型单元网格的大小。原型的计算频率为10～100 Hz，单元大小0.138 m。1:4 缩尺模型的计算频率为40～400 Hz，单元尺寸对应比例相应缩小。

2 壳体声振相似理论推导

2.1 壳体的模态相似性

根据薄壳理论，壳体的无阻尼自由振动有限元方程[10]如下 ：

式中：K为总刚度矩阵；M为总质量矩阵；U为位移列矩阵； ω为固有频率。

假设缩尺模型与原型中相同类型的物理量比值由 λ 来表示，φ′表示缩尺模型的物理量（以下上标“′”均表示缩尺模型的物理量），φ表示对应的原型物理量，则可以得到

将缩尺模型与原型的半径r、长度l以及厚度h按 照相同的比例缩小，可以得到 λr=λl=λh，则壳体缩尺模型与原型的质量矩阵M和刚度矩阵K之间的关系表示为

式中： λl为 缩尺模型与原型的长度之比； λρ为缩尺模型与原型的密度之比； λE为缩尺模型与原型的杨氏模量之比。

缩尺模型的特征方程为

将（3）式代入（4）并与式（1）对比，可得式（5）所示的相似比。

式中， λω为缩尺模型与原型的固有频率之比。

因缩尺模型与原型满足几何相似、边界条件相同，且缩尺模型与原型的特征方程类似，故两者的模态振型相同，固有频率与几何尺寸成反比。

当壳体浸没于水中时，假设水的质量均匀分布在壳体表面，附连水质量与壳体质量叠加得到新的质量矩阵，壳体在水中产生的辐射阻尼与壳体结构阻尼叠加得到新的阻尼矩阵，则求解振动方程可得到壳体在水中的湿模态频率与模态振型。流体的负载力[10]可表示为

式中：p为流体压力列矩阵； ρa为流体密度；R¯为声辐射阻尼矩阵；M¯ 为 流体的等效质量矩阵；S为单元耦合矩阵；U˙为振动速度（U为振动位移）。

壳体在水中自由振动的有限元方程为

当缩尺模型与原型材料相同且壳体接触的流体也相同时，可得到壳体在水中的湿模态频率的相似比如下：

式中， λωf为缩尺模型与原型在水下的固有频率之比。

由式（8）可见，壳体在水中与空气中的固有频率相似规律一致，即固有频率与几何尺寸成反比。

2.2 壳体的振动响应相似性

壳体在受激振动作用下的有限元方程为

式中：C为总阻尼矩阵；F为激励力；U¨为振动加速度。根据上述分析，缩尺模型在受激振动下的有限元方程可表示为

在缩尺模型与原型施加相同的点激励力，则缩尺模型与原型单元节点力满足以下相似比：

当缩尺模型与原型完全相似时，缩尺模型与原型的总质量矩阵及总刚度矩阵的相似比依次表示为

将式（12）代入原型与缩尺模型的受激振动有限元方程式（9）和式（10）中，可得到振动位移响应的相似比为

当壳体浸没于水中，壳体振动时受到流体的反作用，此时在壳体表面产生流体负载力，影响了壳体的振动特性。在流体中，壳体受激振动的有限元方程[10]为

与空气中缩尺模型所采用的分析方法类似，也可得到壳体在水中的振动响应相似比为

2.3 辐射声场的相似性

原型的流固耦合有限元方程[10]可以表示为

式中：Mf为流体的质量矩阵；p为流体的压力；ηf为流体损耗因子； ωf为水下的固有频率。

结合式（2），经计算可以推导出缩尺模型与原型的耦合矩阵相似比为

式中， λρa为缩尺模型与原型的流体密度之比。

采用相似分析方法将式（17）代入式（16），比较缩尺模型与原型的表达式，可以得到如式（18）所示的声压相似比。

式中：pa为水下声压； λr0为空间中测点距离r0相似比。

将式（15）代入式（18），可得到声压相似比为

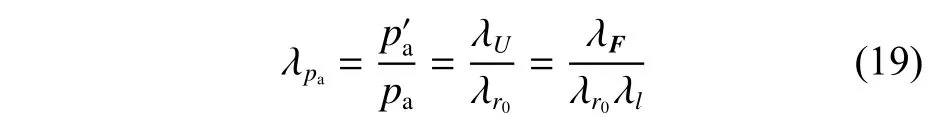
根据辐射效率的定义：

式中：ca为在水中的声速；S为结构表面积；V为结构表面平均振速；Pw为辐射声功率，且可写为

则缩尺模型与原型的辐射效率相似比为

由上式可知，在缩尺模型与原型几何相似且边界条件也相同时，两者辐射效率相同。

根据远场声压[2]表达式：

式中：pmn(r0)为声压，其中m为模态阶数，n为频散方 程 中 轴 向 波 数 解 的 序 号；h(kr)和h(kr0)为第1 类汉克尔函数，其中k为系数；Ym(θ,ψ)为勒让德函数（ θ,ψ为方位角）。

由上述可知，当结构完全相似时，缩尺模型与原型的远场声压表达式相同，若kr=k′r′、kr0=k′r，在远场下的声压相似条件和方位角无关，则缩尺模型与原型的声压指向性相同。

3 加筋圆锥壳模型试验验证

通过对已有加筋圆锥壳模型进行振动响应试验测试，分别得到模型在空气与水下的结构振动响应。试验时，模型两端开口不封闭，通过柔性绳索吊放浸没于水池中，模型内外侧均与流体接触。图2（a）所示为模型及加速度传感器测点的布置图，从1-1～7-1 每组4 个测点，均布在模型四周，其中锥壳顶端设置2 个测点，布置在水平方向和垂向方向；图2(b) 所示为在ANSYS 中分别采用梁单元与面单元模拟加筋构建的圆锥壳有限元模型。首先，采用模态叠加法计算空气中的结构振动响应，然后将有限元模型及其模态数据导入Virtual.Lab Acoustics 声 学 计 算 程 序 中，再 采用FEM-BEM 方法计算模型水下结构振动响应。仿真计算时，流体密度取 ρa=1 000 kg/m3，水中的声速ca=1 500 m/s。加筋圆锥壳模型固有频率与振动响应的计算、测试均为无边界约束的自由状态。

图2 加筋圆锥壳试验测点分布及有限元模型Fig. 2 Distribution of test points and finite element model of stiffened cone shell

对加筋圆锥壳模型结构在空气中的振动响应进行仿真计算。图3 所示为仿真与试验结果的对比。由图可见：试验测试与仿真计算的加速度级响应趋势一致，响应大小也比较接近，但峰值对应频率略有不同，试验测试结果第1 阶峰值频率为106 Hz，采用面单元模拟加筋方式构建的模型第1 阶峰值频率为102 Hz，采用梁单元模拟加筋方式构建的模型第1 阶峰值频率为99 Hz。

图3 空气中振动加速度级的试验与仿真结果对比Fig. 3 Comparison of acceleration level between experimental and simulation results in air

虽然试验测试与仿真计算得到的振动响应结果整体趋势一致，但采用面单元模拟加筋方式所构建模型的振动响应与试验结果吻合更好。其主要原因在于，该方式构建的模型在环肋和纵筋连接处可以模拟实际环肋腹板与纵筋腹板的连接，而采用梁单元模拟加筋方式构建的模型无法模拟实际环肋腹板与纵筋腹板的连接。

通过Virtual.Lab Acoustics 程序计算模型结构在流体耦合作用下的振动响应时，同样对采用两种模拟加筋方式构建的模型进行计算，然后与试验测试结果进行对比，以验证两种模型在计算水下加筋结构振动响应方面的合理性。

图4 所示为两种方式构建的模型水下振动响应加速度级的仿真与试验结果对比。由图4 可见，两者水下计算结果与试验结果基本一致，但部分频率处的振动响应差异明显。其中，采用梁单元模拟加筋方式构建的模型其水下振动响应幅值偏差更大，而采用面单元模拟加筋方式构建的模型其水下振动响应与试验结果吻合更好。其主要原因在于，运用BEM 计算结构水下振动响应时，由梁单元模拟加筋方式构建的模型无法实现环肋及纵筋与流体的耦合作用，表明在考虑流体耦合作用时与流体接触的加筋结构采用面单元模拟更合理。

图4 水下振动加速度级试验与仿真结果对比Fig. 4 Comparison of acceleration level between experimental and simulation results in water

通过对比空气中和水下加筋锥壳模型的试验与仿真振动响应结果，可以发现采用面单元模拟加筋方式构建的模型其振动响应计算结果与试验结果更吻合，其主要原因在于，此方式构建的模型在环肋及纵筋连接处可以更好地模拟环肋腹板和纵筋腹板的连接。当加筋结构与流体接触时，采用上述方式模拟加筋能较好地实现加筋结构与流体的耦合作用。通过对比，还发现采用FEM-BEM混合方法计算圆锥壳水下振动响应的结果与试验结果基本一致，表明采用FEM-BEM 方法计算水下壳体结构振动响应是可行的。

4 复杂加筋锥-柱组合壳结构相似规律计算分析

考虑到采用面单元模拟加筋方式构建的圆锥壳模型仿真计算与试验结果更吻合，故还采用此方式构建复杂加筋锥-柱组合壳模型进行仿真计算。根据声振相似有限元理论，采用FEM-BEM方法并基于ANSYS 和Virtual.Lab Acoustics 计算程序，研究上述组合壳结构的声振相似规律。

首先，在ANSYS 中计算该组合壳结构在空气中的干模态，经模态叠加法计算其振动响应。然后，将ANSYS 中构建的有限元模型与模态数据导入Virtual.Lab Acoustics 程序中，经BEM 方法计算组合壳在水下的湿模态、振动响应和声辐射。其中，组合壳模型的边界条件设置为无约束的自由状态。考虑到实际情况，模型锥段的内外两侧及圆柱段的外侧与流体接触，而圆柱段内侧结构不与流体接触。在计算水下声振响应时，将圆柱段边界元模型网格内侧声压设置为零的边界条件，以模拟柱段内侧不与流体接触。

4.1 加筋锥-柱组合壳固有频率相似性

计算复杂的加筋锥-柱组合壳模型原型及其1:4 缩尺模型在空气与水中的模态，提取前20 阶模态频率中除刚体模态外的固有频率。计算结果如表1 和表2 所示。

由表1 可见，该组合壳原型与其1:4 缩尺模型在空气中的模态频率相似倍率关系均在4 附近，体现出了较好的相似规律，符合模态频率与几何尺寸成反比的规律。

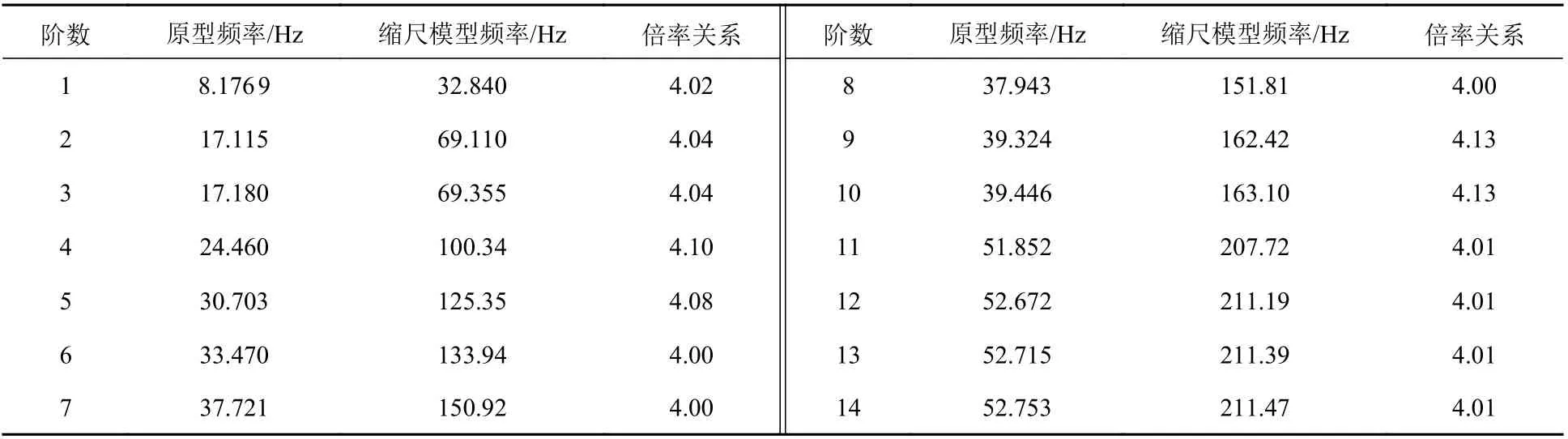
表1 加筋锥-柱组合壳模型干模态频率Table 1 Dry modal frequency of stiffened cone-cylinder combined shells

当此组合壳模型浸没于水中时，在流体耦合作用下壳体固有频率发生了变化并向低频偏移。通过将干模态计算结果导入Virtual.Lab Acoustics程序中，采用BEM 耦合流体作用以计算组合壳的湿模态。由表2可见，组合壳模型与其1:4 缩尺模型模态频率的相似倍率关系都在4 附近。通过固有频率的对比分析，发现该组合壳模型在空气中与水下的模态频率均表现出了模态频率相似比与几何尺寸成反比的规律。

表2 加筋锥-柱组合壳模型湿模态频率Table 2 Wet modal frequency of stiffened cone-cylinder combined shells

4.2 加筋锥-柱组合壳振动响应相似性

在空气中和水下的复杂加筋锥-柱组合壳模型具有相同的激励点与振动响应测点提取位置。其中，原型在坐标（0,0,1）处施加x方向的单位激励力，原型振动响应测点提取位置位于锥壳与柱壳交接处，坐标为（8,0,3.5）。缩尺模型的激励点和振动响应测点与原型所提取的位置对应。在ANSYS 中采用模态叠加法计算复杂加筋锥-柱组合壳模型在空气中的振动响应。原型计算频率范围为10～100 Hz，频率间隔1 Hz，1:4 缩尺模型计算频率范围为40～400 Hz，频率间隔为4 Hz。图5 所示为复杂加筋锥-柱组合壳模型原型与缩尺模型在空气中振动加速度级响应曲线对比，图6 所示为考虑了流体耦合作用时的两者振动加速度级响应对比。

图5 空气中的加筋锥-柱组合壳振动加速度级响应对比Fig. 5 Comparison of vibration acceleration level response of stiffened cone-cylinder combined shells in air

由图5 可见，在激励力及激励点位置相同、结构尺寸完全相似的情况下，缩尺模型与原型的振动响应曲线趋势一致，对应频率处的振动加速度级相似，模型振动响应与几何缩尺比成反比，满足式（13）表示的空气中模型振动响应相似比。

图6 水下加筋锥-柱组合壳的振动加速度级响应对比Fig. 6 Comparison of vibration acceleration level response of stiffened cone-cylinder combined shells in water

由图6 可见，当壳体浸没于水下时，流体耦合作用对结构水下振动响应产生了明显影响。相比空气中的模型，水下模型的振动响应曲线总体趋势一致但峰值更密集，其主要原因在于，流体的附连水质量效应导致结构固有频率降低。尽管受到流体耦合作用，缩尺模型与原型的振动加速度级响应曲线仍趋于一致，表明模型在水下受激振动时也能够表现出较好的振动相似性，且模型与原型的振动响应与几何缩尺近似成反比，符合式（15）表示的水下模型振动响应相似规律。

4.3 加筋锥-柱组合壳辐射声场相似性

计算复杂的锥-柱组合壳模型水下声辐射。将流体耦合作用下的模型振动位移响应施加到边界元模型，计算壳体在无限域流场中的辐射噪声，缩尺模型与原型施加激励力的位置、方向和大小均相同，取原型与缩尺模型对应位置的场点辐射声压进行分析。其中，原型场点坐标为（6，0，15），缩尺模型对应场点坐标为（1.5，0，3.75）。图7 所示为加筋锥-柱组合壳模型对应场点的水下辐射声压级曲线，由图可见，原型与缩尺模型对应场点的辐射声压级曲线基本一致，因辐射声场所受影响因素较多，部分频率点处声压存在一定偏差，但整体表现出辐射声压的相似性。

取缩尺模型与原型声场中对应的场点，提取其频率及辐射声压，表3 所示为频率比为4 倍的频率及其对应的辐射声压相似比。结合式（19）可知，缩尺模型的长度比为4，测点距离比为4 时，声辐射相似比为16，而表3 中所示各对应点的辐射声压倍率都在16 附近。

由表3 和图7 可见，在缩尺模型和原型对应的分析频率中，声压频率响应曲线趋势总体一致，表明声辐射具有相似性，且满足式（19）声压与缩尺比和场点距离比的乘积成反比的相似规律。

图7 水下加筋锥-柱组合壳的场点辐射声压对比Fig. 7 Comparison of field radiated sound pressure of stiffened cone-cylinder combined shells in water

表3 辐射声压相似关系Table 3 Similarity relation of radiated sound pressure

图8 所示为水下加筋锥-柱组合壳及其缩尺模型对应位置的声压指向性图。图8（a）为原型60 Hz 处声压指向性，图8（b）为缩尺模型240 Hz处声压指向性。其中，原型指向性半径为60 m，缩尺模型指向性半径为15 m，指向性图均位于xoy面上。对比图8 中水下组合壳模型及其缩尺模型可知，在满足几何相似、材料和流体属性相同、载荷及激励位置相同的条件下，缩尺模型在水中的声压指向性与原型的基本相同。

图 8 水下加筋锥-柱组合壳的辐射声压指向性对比Fig. 8 Comparison of acoustic directivity of stiffened cone-cylinder combined shells in water

5 结 论

本文使用面单元模拟加筋方法构建了复杂加筋锥-柱组合壳模型及其缩尺模型，采用FEMBEM 混合方法建立了该组合壳模型在空气和水下振动有限元方程及流体中的模型声学有限元方程，推导出了此复杂组合壳振动、声-固耦合振动及水下声场之间的相似比。通过模型试验，验证了采用FEM-BEM 混合方法进行声振求解的准确性，研究了复杂加筋锥-柱组合壳结构声振相似规律，主要得到如下结论：

1） 对水下壳体结构进行声振仿真计算时，若加筋结构与流场存在耦合，采用面单元模拟加筋方法比梁单元模拟加筋更合理。

2） 对于复杂加筋锥-柱组合壳结构，在材料属性、边界条件和激励力相同时，其模态频率与几何缩尺比成反比，对应频率的模态振型相同；在激励力相同时，复杂组合壳结构的振动响应与几何缩尺比成反比，而声压与几何缩尺比和场点距离比的乘积成反比。

3） 缩尺模型与原型的辐射效率及声压指向性相同。

本文研究结果可为水下复杂加筋壳结构的声振缩尺模型试验提供支撑和依据。