基于变权重的水库滑坡稳定性模糊综合评价
2022-04-25高明贺可强刘洪华王忠胜全恩伟
高明,贺可强*,刘洪华,王忠胜,全恩伟
(1.青岛理工大学土木工程学院,青岛 266400;2.青岛地质工程勘察院(青岛地质勘查开发局),青岛 266100; 3.山东华通路桥工程有限公司,临沂 276000)
滑坡影响范围大、治理难度高、危害性强,水库型滑坡大规模的坡体下滑会堵塞河道、阻碍交通,造成巨大的经济损失,甚至导致人员伤亡。因此,如何准确确定滑坡所处的稳定性状态,从而及时预警或采取有效的防治措施,对预防巨大灾害的发生至关重要。
中外针对滑坡稳定性的评价主要分为基于假定简化模型计算的方法和基于统计学、数学的不确定性方法[1-4]。近年来,随着人们对滑坡非线性的认识,模糊数学综合评价法作为一种非线性分析方法,以其模型简单、多层次和定量化的突出优点[5],在滑坡稳定性评估、预测工作中得到了广泛的应用并不断发展[6-8]。而在其应用过程中,评价指标的选择及其权重的确定是研究的难点和重点。Beyabanaki等[9]得出地下水、土体参数、天气条件等均为滑坡稳定性影响因素指标;朱德明等[10]对金沙江白格滑坡进行野外调查,并结合其实际工程地质条件及残留体变形特征选取评价指标;李聪等[11]运用层次分析及关联函数确定指标主客观权重,并将其赋权得到动态权重;王春燕等[12]通过灰色关联分析法得到一级模糊综合评价因素权重值;宋华艳等[13]借助地理信息系统(geographic information system,GIS)空间加权叠加分析技术对评价因子进行分析得到滑坡易发性分级。这些研究都是为了客观评价滑坡稳定性,减少滑坡稳定性评价结果被主观因素干扰,合理评价滑坡稳定性,减少事故的发生。
综上所述,虽然目前存在各种滑坡稳定性状态评价指标,但由于其结构层次和相互影响程度较为复杂,很难系统地建立它们之间的关联性[14];此外,常规赋权方法得到的评价结果仅代表评价时滑坡体的稳定性状态,但随着其内外部条件的不断改变,滑坡变形情况也会发生变化,应该将这种情况考虑在评价指标的赋权中,使评价结果随着变形情况发生动态变化,从而更加符合客观实际。
鉴于此,现结合水库型滑坡内、外部条件及相关规范[15-16]规定选择滑坡稳定性影响因素,基于指标因素间的客观规律和相关函数,确定各评价指标对稳定性等级的隶属度,运用层次分析法和专家经验确定评价指标权重,并结合实际监测数据的变化对权重进行改变,构建模糊综合评价模型;并以三峡库区白水河滑坡为例,进行变权重稳定性模糊综合评价,验证该方法的可行性,以期为类似滑坡稳定性评价提供科学思路。
1 滑坡稳定性评价指标的选取
影响水库型滑坡稳定性的因素繁多,关系错综复杂,因此,确定科学可靠、系统完整的指标体系是滑坡稳定性评价的前提。滑坡内部因素对坡体稳定性产生直接影响,坡度和坡高会影响坡体滑动面剩余下滑力;岩体物质组成决定了坡体抗外部荷载和人为扰动的能力,不同的组成物质其渗透性也不尽相同,从而影响水径流与入渗的程度。此外,外部环境条件也会间接影响坡体稳定性,水库型滑坡受库水位波动以及降雨等影响较大,其所在地区大部分地表水系较发育,并且受季节性冲沟冲刷的影响,滑坡前缘极易出现错移的现象。
为了使评价指标体系能全面、准确地反映对滑坡稳定性状态的影响程度,在指标体系设计时,尽量确保其科学完整、客观实用,同时将影响程度小的评价指标筛除,避免因素过多而分散主要指标的作用。综合研究中外典型滑坡稳定性影响因素,结合水库型滑坡成因和地质水文结构等特征并考虑各指标监测的可操作性,将滑坡稳定性评价指标概括为4项10个因素,如表1所示。

表1 水库型滑坡稳定性评价指标
2 滑坡稳定性评价模型
基于滑坡监测数据和相关稳定性安全指标等,运用层次分析法将复杂的滑坡稳定性问题的定性和定量因素分层简化,计算各层次结构的权重;运用模糊综合原理,将定性因素定量化并进行评价。
2.1 确定稳定性评价指标集和评语集
确定影响效果明显并且具有代表性的m个指标,分别定义为u1,u2,…,um,则
U={u1,u2,…,um}
(1)
即评价指标集。
确定评价结果等级为n个,分别定义为v1,v2,…,vn,则模糊综合评价评语集可表示为
V={v1,v2,…,vn}
(2)
2.2 确定隶属度及模糊关系矩阵
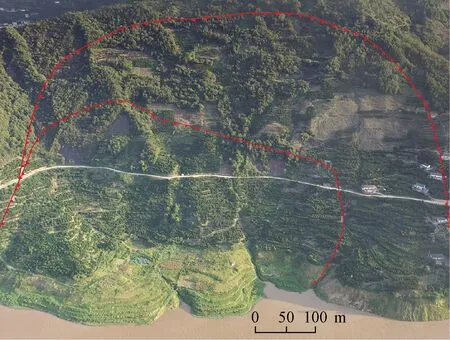
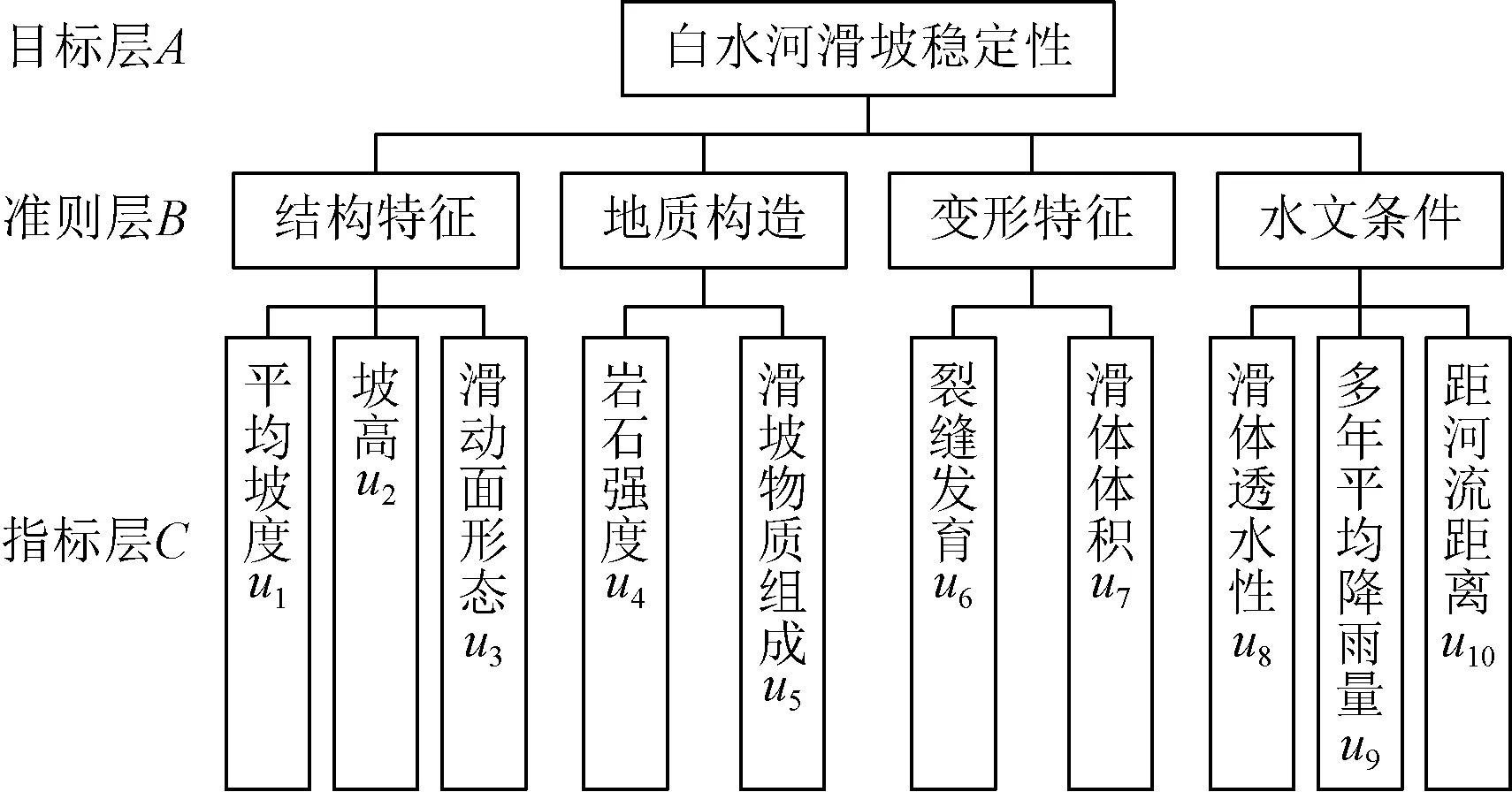
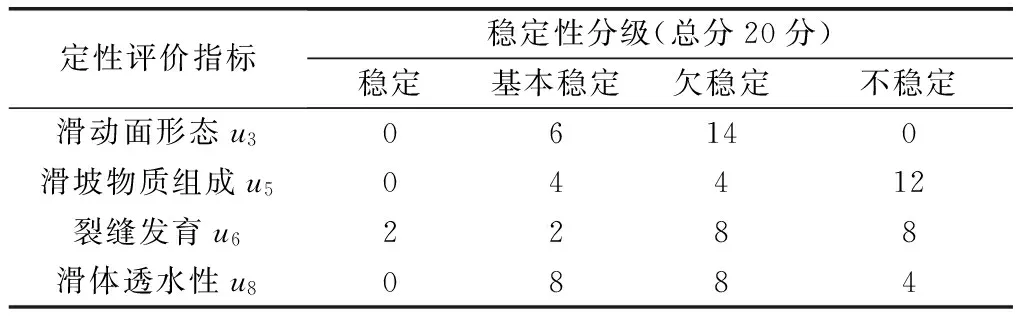
定量评价指标根据数值大小和评价等级分为4个范围,可统一表示为: (3) (4) (5) (6) 其中,对于数值越大越好的定量指标,采用升半梯形分布隶属度函数,对于数值越小越好的定量指标,采用降半梯形分布隶属函数[18]。 运用上述方法,基于评价指标集和评语集,首先确定每个单因素指标隶属度子集合Ri,进而确定如下形式的模糊关系矩阵: (7) 式(7)中:rij为指标ui隶属于评价等级vj的程度,取值范围0~1。 选用的权重不同得到的结论也会完全不同。 2.3.1 应用层次分析法确定初始权重 将复杂的滑坡稳定性评价问题按照元素类别不同分解为目标、准则、指标三个层次,在此基础上进行分析。 为了提供下层元素对上层元素影响程度的具体可靠数据,采用1~9标度法[19],比较同层元素相对重要性,构成判断矩阵: (8) 式(8)中:uij>0,表示对于与之相关的上一层元素而言,ui相较于uj的重要性数值;uij=1/uji;uii=1。 采用特征根法计算各元素权重,过程为 (9) (10) 则W=(W1,W2,…,Wm)即属于同一上级的各评价指标的初始权重向量。 一致性检验的计算公式为 (11) 式(11)中: (12) (13) 式中:RI为随机平均一致性指标,其取值如表2所示;CI为一致性指标;λmax为矩阵的最大特征根;Wi为参与计算指标的初始权重;m为指标数量。如果计算得出CR>0.1,则判断矩阵不一致,需重新取值;若CR<0.1,则矩阵一致性通过检验;当矩阵阶数为1和2时,RI=0,此时矩阵不会出现权重分配不一致,自动通过检验。 表2 随机一致性指标RI值 2.3.2 基于评价指标的变动进行变权重 常权重仅表示在理想状态下各评价因素之间的相对重要性,可能会隐没较差等级的评价指标对评判结果的影响,而变权重同时还考虑了各因素之间的均衡性,体现了在不同目标等级状态下各个因素不同的组态变化。为减少确定评价指标初始权重时的主观因素并避免关键性指标被平均化,使用变权理论修正各指标权重,以突显各指标在评价中的均衡性。 采用惩罚型变权向量[20]: W(x)=[ω1(x),ω2(x),…,ωm(x)] (14) 并采用Hardarmard乘积计算: (15) 式中:W为常权向量,W=(W1,W2,…,Wm);S(x)为状态变权向量,S(x)=[S1(x),S2(x),…,Sm(x)];选用均衡函数[21]: (16) 由权重向量W与模糊关系矩阵R可得评价结果S为 S=W°R=[W1,W2,…,Wm]° (17) 式(17)中:°为模糊算子。 白水河滑坡位于秭归县白水河村,属于典型的三峡库区深层堆积层滑坡,毗邻长江南岸。“靠椅状”滑坡,整体坡度约30°,南部高北部低,平均厚度大约为30 m,以岩体材料分界,后缘最高处约400 m,坡度约36°;中部由于道路修建等出现多级平台,较为平缓;前缘135 m以下长期处在江水浸没中,约120 m高程以下为坡度约29°的陡坎。滑体体积1 260×104m3。滑坡全貌如图1所示。 图1 白水河滑坡全貌 根据白水河滑坡地层勘探,第四系残坡积碎石土和块石占比较高,粉质黏土所占比例也很大,结构松散,靠近滑面处多为砂岩,孔隙率变化较大,含水性不均匀。下伏基岩主要成分是含碳质粉沙质泥岩,大多数呈现中风化—强风化状,岩体完整性不同,裂隙高度发育切割岩体。白水河是历史上频繁滑动的堆积体顺层滑坡,年平均降雨量约982 mm,其滑动和变形大多出现在雨季,主要表现为裂缝、坍塌和下沉。2006—2015年间,每逢雨季,滑坡均会有多条地裂缝出现或发育,呈羽状或阶梯状,宽约50 mm,延伸超过50 m,滑坡局部出现变形和拉裂坍塌。 将表1元素按属性不同分为目标层A、准则层B和指标层C,如图2所示。图2中指标层各元素即构成了模糊综合评价指标集U。 图2 白水河滑坡稳定性评价层次体系 根据《滑坡防治工程勘查规范》[22]中12.4.6条规定确定评语集V,即将滑坡稳定性状态分为稳定、基本稳定、欠稳定、不稳定4个等级。 根据白水河滑坡工程概况,提取出稳定性评价指标所需要的数据。 选择有经验的专家以总分20对定性指标打分,如表3所示,归一化标准处理后得单指标隶属度矩阵为 表3 白水河滑坡定性指标专家打分 R3=[0 0.3 0.7 0] (18) R5=[0 0.2 0.2 0.6] (19) R6=[0.1 0.1 0.4 0.4] (20) R8=[0 0.4 0.4 0.2] (21) 定量指标以滑坡平均坡度为例,白水河滑坡平均坡度为29°~34°,根据2.2节隶属度函数计算公式[式(3)~式(6)],可得平均坡度对稳定性等级的隶属度为 R1=[0 0.5 0.5 0] (22) 同理可得其他定量指标的隶属度: R2=[0 0 0 1] (23) R4=[0 0.2 0.8 0] (24) R7=[0.8 0.2 0 0] (25) R9=[0 0 0.5 0.5] (26) R10=[0 0 0 1] (27) 由各指标隶属度即构成模糊关系矩阵R。 构造各层次子因素之间的比较判断矩阵。一级指标判断矩阵为 (28) 基础指标层各因素判断矩阵为 (29) (30) (31) (32) 其中,A-B为目标层A对应的下层准则层B;B1-Ci为准则层第一个类型相应的下层指标层各元素,其余同理。 表4 白水河滑坡稳定性评价指标权重 表5 一致性检验结果 在滑坡发生变化时,将实际工程监测数据作为动态指标的数据来源。 首先需要合理确定均衡函数变权系数t,取值为0~1,根据相关研究,取t>0.5时更趋向于常权结果,忽视了因素间的平衡关系,而取t<0.5时的结果弥补了这一不足。因此,若保守评价或某个特殊因素对体系安全性影响重大,则取t<0.5,相反取t>0.5。 文献[23]中将该变权公式应用于储气库舱体稳定性评价中,并取t=0.2计算,取得了良好的评价效果。而滑坡稳定性影响重大,评价应严格,偏向保守严谨,故选择t=0.2进行计算,根据式(15)和式(16),结果如表4所示。 将指标层各单指标隶属度矩阵与其权重向量进行计算,即得准则层因子对评价等级的隶属向量,以结构特征因素的评价向量为例: =[0 0.312 0.528 0.160] (33) 则准则层各因素的评价向量为 (34) 将RB与相应的权重向量通过加权平均型模糊算子运算可得滑坡稳定性对评语集合的隶属向量为 S=WB°RB =[0.17 0.12 0.32 0.39]° =[0.088 0.200 0.401 0.311] (35) 根据最大隶属度原则,从向量矩阵中最大值出 现的位置,可判断其对应的评语集结果,即白水河滑坡处于欠稳定状态。 采用变权重向量与隶属度矩阵进行运算,得出准则层各因素对评语集的隶属向量为 (36) 则变权重得到的稳定性对评语集合的隶属向量为 (37) 可得白水河滑坡处于不稳定等级。 依据滑坡的监测数据分析(来源:湖北长江三峡滑坡国家野外科学观测研究站),在降雨和库水位波动等的耦合变动作用下,白水河滑坡稳定性稍差,2003年三峡水库蓄水水位高度达到135 m,坡体出现明显滑动周界以及滑动面,某些监测点宏观位移甚至已接近3 m。并且文献[24]通过试验与数值模拟也得出的滑坡在库水位反复波动干扰下会造成失稳情况。本文提出的基于变权重水库滑坡稳定性模糊综合评价方法得出的稳定性结果与现场实际情况基本一致,滑坡变为欠稳定状态。 此外,根据白水河滑坡监测数据,滑坡区的裂缝发育、库水位升降、年降雨量等都在发生变化,以水位波动及降雨引发的裂缝变形为例:水位于2007年2—7月首次由154 m下降到145 m,滑坡东侧和后缘边界基本贯通,西侧裂缝大量展布;2008—2014年,在强降雨的影响下,滑坡局部出现浅层坍滑,裂缝依然存在但未发育;2015年6—7月,降雨频繁,总降雨量达到约215 mm,白水河滑坡出现了较大宏观变形,滑坡局部变形速率将近14.60 mm/d[25]。结合3.5节可以得知,分别运用初始权重和变权重进行模糊综合评价,最终得出了不同的结果,这正显示了随着时间的推移,滑坡变形情况发生了变化,而变权后的评价结果随着变形情况也发生动态变化,更加符合客观实际。 针对水库型滑坡的特点,分析了影响滑坡稳定性因素并考虑因素间的关联性,提取重要因素,构建评价指标体系;提出结合变权重的模糊综合评价模型,以白水河滑坡为例,进行稳定性综合评价,进行了实例验证,并给出防治对策。 (1)研究水库型滑坡特点,结合理论分析和规范规定,筛选出适合该研究对象的评价指标,分为结构特征、地质构造、变形特征、水文条件4大项,共包含10个因素。 (2)采用定性与定量相结合的方法计算指标隶属度;运用层次分析原理得出评价指标权重,并根据滑坡特征的变化进行变权重,建立模糊综合评价模型。 (3)评价结果表明,白水河滑坡稳定性不佳,且变权前后评价结果有欠稳定和不稳定的区别,体现了变权的科学合理,评价结果随着变形情况发生动态变化,更符合客观实际。

2.3 确定初始权重并进行变权重
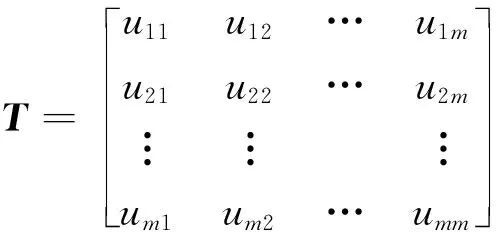





2.4 模糊综合评判结果
3 白水河滑坡稳定性的变权重模糊综合评价
3.1 白水河滑坡工程概况
3.2 白水河滑坡评价因子的层次分析
3.3 建立模糊关系矩阵
3.4 确定初始权重及变权重

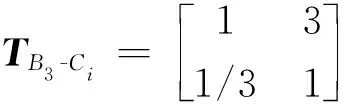

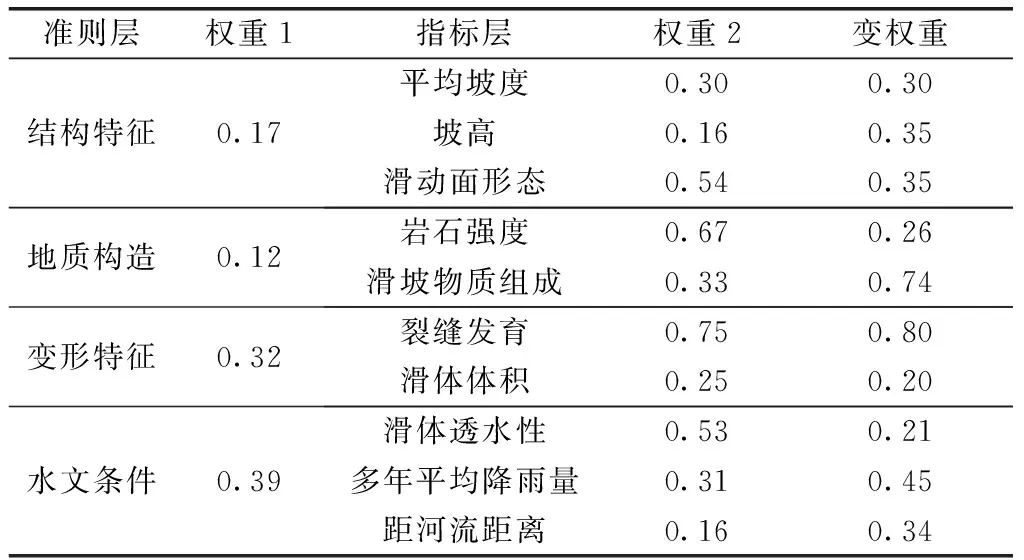
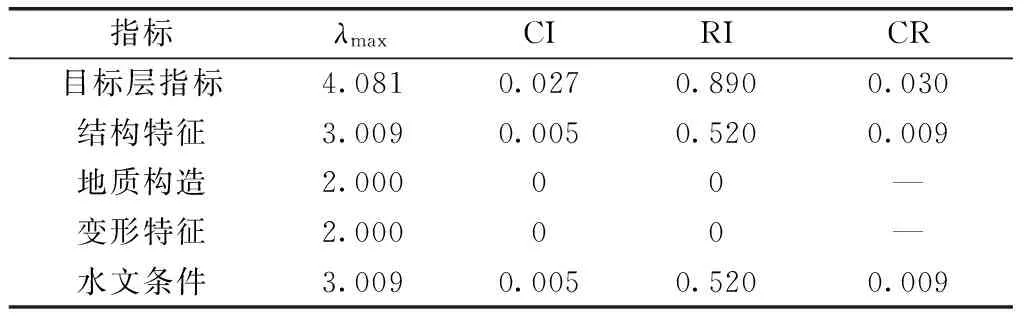
3.5 白水河滑坡稳定性综合评价
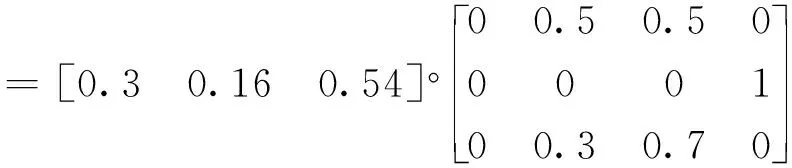

3.6 白水河滑坡稳定性评价结果分析
4 结论
