计及停电损失的电力系统黑启动分区策略

李婧斐，黎琦，罗萍萍，方日升，姚历毅，林济铿

(1. 上海电力大学电气工程学院，上海 200090；2. 国网江西省电力有限公司抚州供电分公司，江西 抚州 344000；3. 国网福建省电力有限公司电力科学研究院，福州 350007；4. 国网福建省电力有限公司漳州供电公司，福建 漳州 363000；5. 同济大学电子与信息工程学院，上海201804)

0 引言

定期制定黑启动及系统恢复应急预案，已变成各级电力公司的日常工作[1 - 3]。该应急预案一般由系统分区方案、分区黑启动方案组成，而分区黑启动方案由黑启动路径[4 - 5]、网架恢复[6 - 7]以及负荷恢复[8 - 9]等组成。不难看出，系统分区是黑启动及系统恢复的重要步骤和环节，直接影响着系统恢复方案的总时间及相应停电损失，因此科学合理地确定分区方案的研究即成为一个非常有意义的研究课题。

近年来国内外学者已对电力系统黑启动并行恢复分区问题进行了大量的研究。相关研究大致可以分成两类。

第一类，基于复杂网络理论进行的系统分区方法。文献[10]采用谱聚类算法，将电网拓扑对应的Laplace矩阵的特征向量通过k-means聚类得到子系统分区方案。文献[11]基于GN(Girvan and Newman)分裂算法，实现电网的快速自动分区，并给出了子区并列顺序；文献[12]将分区过程分为“凝聚”与“分裂”两个阶段，凝聚阶段根据负荷的重要程度将厂站节点进行聚合得到简化网络，分裂阶段根据线路的重要程度直接断开相关线路而得到系统分区；文献[13]考虑停电前系统的潮流分布，采用改进标签传播算法实现子系统的划分。上述文献均是从复杂网络理论角度进行系统分区，使得子系统内部节点联系紧密而子系统之间联系较弱，但由于忽略电网的电气特性，难以考虑如分区功率平衡量等约束条件，使得其所得到的分区只是网络拓扑方面是最优的，并不一定保证分区间的电气特性是最优的。

第二类，基于0- 1整数混合规划技术的系统分区方法。其基本思想是将电力系统并行恢复最优分区问题构建为混合整数规划模型，并采用商业软件求解。文献[14]建立以联络线数量最少为目标的混合整数线性规划模型，并引入“割”约束以获得多个子系统划分方案供调度人员选择；文献[15]讨论了分区对系统可观测性的影响，并基于节点可观测度提出了相应的拓扑图简化方法以缩减解空间的范围。文献[16]提出计及分区间联络线数量与功率交换最小的电力系统最优分区模型，并采用基于递归二分思想对网络进行多次划分，相应降低了分区问题求解的复杂度，但未引入连通性约束，可能存在子系统内部不连通的问题。

上述黑启动分区研究未能充分考虑分区后子系统并行恢复过程的影响，大多是在求得最优分区方案后，再进行子系统的恢复。黑启动子区域的划分是为了加快系统的恢复过程，相应地子系统并行恢复效果应是衡量分区方案优劣的重要指标之一，因此有必要在进行系统分区模型中考虑该分区方案对系统恢复进程的影响。文献[17]构建了以用户停电损失最小为目标的混合整数规划模型，在求解最优分区的同时，考虑了子系统DG、负荷的恢复问题，但并不能保证子系统在最短的时间内实现负荷恢复的最大化。文献[18]在谱聚类算法的基础上，建立了以系统恢复时间最短的分区优化模型，并基于粗糙集理论对初始分区进行修正，相应计算时间较长，在对需调整的机组进行筛选时，有可能会遗漏某个机组，导致所得分区并不一定是最优分区。

针对已有研究的不足，本文提出了计及子系统并行恢复过程影响的系统最优分区模型及求解算法。该模型近似计及了分区恢复时间的影响，并以分区停电损失及分区间的联络线数目最小为目标函数，以机组归属唯一性、分区功率平衡、分区连通性等为约束条件。该模型为复杂的混合整数非线性规划模型，直接求解比较困难，本文提出了分解求解策略，即把该问题分解为单纯的已知各负荷点恢复时间的分区问题和已知分区的各子系统恢复问题，此时描述该两个子问题的模型均为混合整数线性规划问题，可分别采用CPLEX求解器直接求解，通过两个子问题之间的迭代求解，即可获得原模型的解。算例证明了本文模型的有效性。

1 计及子系统恢复过程影响的系统最优分区问题的新模型

电力系统并行恢复是指在电网发生大面积停电之后，根据电网黑启动电源的个数，将电力系统划分为多个子区域同时进行恢复供电，并经子系统同期互联而实现整个系统恢复供电。系统最优分区问题实质上是图分割问题，但与传统的图分割问题不同，黑启动并行恢复分区问题具有以下几个特点[19 - 21]：1)每个子系统必须包含一个黑启动电源；2)各子系统规模不宜相差过大，否则会产生较长的并网等待时间；3)各子区域内部必须是连通的，以避免部分网络及负荷无法恢复。

电力系统并行分区的目的是为了加速全网恢复，尽快恢复停运的火电机组，减少重要负荷的停电损失，因此有必要在分区时考虑各负荷节点的停电损失；同时子系统间联络线的恢复需要经过电压检验、合闸角调整及频率调整等复杂的同期操作或合环操作，联络线的数量影响后续的系统同步并列过程，因此在分区时应使子系统之间的联络线数量尽量少。考虑以上两个因素，建立如下的目标函数：

(1)

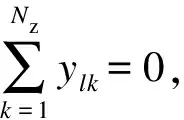
子系统分区模型的约束条件为：

1)黑启动电源约束

(2)

式中：bi为节点i是否为黑启动电源节点，若节点i为黑启动电源，则bi=1， 否则bi=0； 式(2)表示每个区域必须有一个黑启动电源节点。

2)节点支路分区约束

(3)

(4)

式(3)表示每个节点只能属于一个分区。式(4)表示每条支路最多只能属于一个分区，当某条支路不属于任何一个分区时，表示该支路为联络线支路。

3)连通性约束

为保证各子区域内部连通，子区域之间保持孤立，本文基于网络流理论构建子系统连通性约束。网络流理论基本原理为：从系统中源点注入流量，流量通过线路到达每一个节点，所有节点消耗单位流量，当每一个节点都有流量到达时，则可以确保网络的连通性。因此，可将黑启动机组节点定义为系统源点，待启动机组及负荷节点定义为汇点，当网络满足网络流约束时，则可保证所得子区域的连通性。定义整数变量Flk为子系统k中线路l上的虚拟流量，同时规定由节点编号小的节点流向节点编号大的节点为线路虚拟流量的正方向。

(5)

(6)

(7)

(8)

(9)

式中：M为一足够大的正数；l(m,i)表示终点为i的支路；l(i,n)表示起点为i的支路。式(5)表示虚拟流量仅在子系统内部线路上流动，区间联络线上无流量，ylk为0- 1变量，ylk=1意味着Flk≥1， 即线路上有流量，ylk=0意味着Flk=0， 即线路上无流量。式(6)表示除黑启动电源节点外，其他节点消耗的流量值大于等于1个单位。式(7)表示子系统内除黑启动电源外，其他节点流入的流量大于1。式(8)表示黑启动电源节点流出的流量等于该区域节点总数减1，式(9)表示黑启动电源节点流入的流量为0。

4)分区功率平衡约束

(10)

式中：Punb为每个子区域所允许的最大功率不平衡量；Pi,d为节点i的有功负荷；Pi,g为节点i处机组额定功率，式(10)表示每个区域的功率不平衡量必须在阈值范围之内。

5)其他约束

yl(m,n)k=xmkxnk∀k,∀l

(11)

式中xmk、xnk分别为支路l首末端的节点是否属于区域k的0- 1变量，该约束表示若支路l两端都为子区域k的节点，则该支路为区域k内的支路。将该式进行线性化处理后，可用式(12)表达。

(12)

此外若节点为子系统k内的节点，则与节点相连的所有支路中必有一条支路为区域k内的支路。

(13)

2 求解策略

由式(1)—(13)组成的模型是一个大规模混合整数非线性规划问题，直接对其求解存在一定的困难。因此，本文提出了迭代求解的策略。其基本思想如下：首先采用迪杰斯特拉算法计算各负荷节点i到子系统k黑启动电源点的最短恢复路径，根据最短路径法进行初始分区，并根据该初始分区确定各个负荷节点的初始恢复时间Tik； 然后，基于负荷节点的恢复时间Tik， 进行分区的优化和更新，获得新的分区，然后再根据新的分区，更新各个负荷节点的恢复时间Tik； 如此反复迭代，直至收敛，也就得到了最佳分区。

2.1 子系统中负荷节点恢复时间的计算

对于既定的分区，各个子系统的最佳恢复过程是使得其分区的停电损失最小(或系统发电能力恢复最快)，可通过求解其最优恢复模型而获得。本文建立子系统最佳恢复模型，获得其最佳恢复过程；相应地也就获得子系统中各个负荷节点的恢复时间Tik。本文所构建的子系统最佳恢复模型如下。

将子系统恢复过程分为NT个时段，每一时段时间长度为ΔT， ΔT为恢复一条线路及变电站的时间，NT为分区负荷节点到最近黑启动路径所需要经过的线路数。相应地，以停电损失最少的子系统最优恢复模型目标函数为：

(14)

子系统恢复的约束条件如下。

1)发电机爬坡约束

火力发电机启动过程机组出力特性采用近似简化启动特性曲线，分为发电机厂用电启动、发电机并网运行和发电机达到最小出力开始向上爬坡3个阶段，如图1所示。

图1 发电机启动出力曲线Fig.1 Output curve during the generator starting

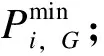
(15)

(16)

(17)

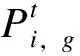
2)机组启动时间约束

(18)

(19)

3)直流潮流约束

为简化模型，加快求解速度，本文采用直流潮流对网络进行建模，直流潮流约束如下：

(20)

4)其他约束

系统中各个设备的恢复过程须满足相应的恢复顺序约束如下。

(1)负荷与发电机恢复时，其所相连的母线必须处于恢复状态。

(2)输电线路恢复时，其端点的母线必须恢复。

(3)母线、输电线路、负荷、发电机一旦恢复之后便不再失电。

由目标函数式(14)及约束(15)—(20)组成的模型为混合整数线性规划问题，可以直接调用求解器CPLEX进行求解，而获得子系统的最佳恢复过程的同时，相应获得子系统中各个负荷节点的恢复时间Tik。其具体求解过程如下：

(1)获得既定分区内的所有机组参数，网络参数及负荷参数；

(2)根据分区负荷分布，确定NT；

(3)构建如式(14)及约束(15)—(20)组成的模型；

(4)调用CPLEX求解由(3)构建的模型；

(5)获得分区近似恢复顺序，相应获得分区中各个负荷的恢复时间Tik。

2.2 最佳分区的求解过程

基于2.1节得到的各个负荷的恢复时间，本文进一步给出式(1)—(13)分区模型的求解算法。具体算法如下：

1)输入全网的网络参数，确定黑启动机组所在位置，确定子区域个数。

2)将线路赋权为电抗值，采用迪杰斯特拉算法计算各节点到黑启动电源节点的最短电气距离，根据电气距离形成初始分区方案。

3)利用2.1节所提出的子系统中负荷节点恢复时间的计算方法，计算各个分区中的各个负荷恢复时间。

4)基于所得到的各个节点负荷恢复时间，由式(1)—(13)所组成的模型是一混合整数线性规划模型，调用CPLEX求解器进行求解，可获得分区方案。

应用所提出的ACMLGD结合文本挖掘和情感分析技术，提取在线评论中正面评价、反面评价及综合评分等信息开发了自动一致性系统，该一致性系统可集成到现有的ERP系统中，用于支持企业的大型群决策活动，也可用于集结互联网产品用户偏好、挖掘发现客户总的一致性意见。现以自动计算面向在线客户偏好的大群客户偏好为例，说明ACMLGD的应用。

5)判断当前的方案和上一次的方案是否有区别，若区别很小或没有区别，计算结束，得到最优的分区方案；否则，转向3)。

所提算法求解流程图如图2所示。

图2 算法流程图Fig.2 Flowchart of algorithm

3 算例分析

本文基于C语言编程实现上述分区算法，并以修改后的IEEE 39节点系统和某实际省级电力系统为算例验证了本文模型算法的正确性和有效性。

3.1 IEEE 39节点系统

IEEE 39节点含有46条支路、10台发电机组，节点30、节点31、节点34为黑启动机组所在节点，且均在0时刻同时启动。重要负荷权重设为1，其他非重要负荷权重设置为0.3，假设节点8、16、18、27所在负荷为重要负荷。

首先，采用迪杰斯特拉算法计算各节点到黑启动电源的电气距离得到初始分区结果如图3所示，初始分区方案未考虑各负荷恢复时间，各子区域规模相差较大。针对初始子系统划分，调用分区恢复模型得到3个子系统的恢复方案，全系统经13个时段恢复完成。

图3 IEEE 39节点系统初始划分方案Fig.3 IEEE 39-bus system initial partition result

采用本文2.2节最优分区算法，经过2次迭代后收敛，最终所得的分区结果如图4所示。为说明本文算法的有效性，图4中同时给出了文献[16]和文献[22]方法子区域的划分方案。

图4 IEEE 39节点系统分区方案对比Fig.4 Comparison of IEEE 39-bus system partition result

由分区方案可以看出3种方法中存在如下两个方面的不同。

1)节点39所在机组的分区归属不同，39号节点到子区2的黑启动电源至少需要经过5条支路，而到子区1的黑启动电源则仅需经过3条支路，从机组恢复结果来看，在本文和文献[16]分区恢复方案中，机组39在时段3从子区1黑启动电源获得启动功率开始启动，而在文献[22]所得分区恢复方案中，机组39在时段5从子区1黑启动电源获得启动功率。故本文分区算法相对于文献[22]算法，使得39号节点的发电机更快地启动。

2)节点18、39所在负荷的分区归属不同，其中负荷18为重要负荷，从负荷恢复结果来看，在本文所得分区恢复方案中，负荷18在时段8恢复，而在文献[16]和文献[22]所得分区恢复方案中，负荷18在时段12恢复。故本文分区算法相对于文献[16]和文献[22]方法，重要负荷更快地得到恢复。

表1为采用3种方法得到的分区不平衡量对比结果，本文所得分区不平衡功率略小于文献[16]和文献[22]，各子系统规模相当，故本文方法所得分区结果更有利于整个系统的快速恢复。

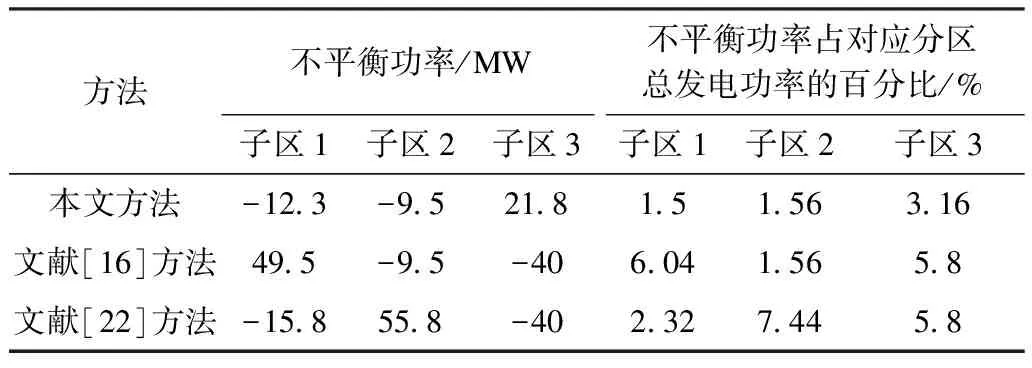
表1 采用3种方法得到的分区不平衡量对比结果Tab.1 Comparison results of unbalanced power by three methods

图5表示采用本文方法与文献[16]、文献[22]方法所得到的分区进行分区恢复所得到的各个恢复时段系统负荷的恢复情况。图中横坐标表示恢复时段，纵坐标表示加权负荷恢复量，曲线1、曲线2、曲线3分别为本文所得分区方案中子区1、子区2、子区3的负荷恢复曲线，曲线4为本文分区方案全系统负荷恢复曲线，曲线5、曲线6分别为文献[16]、文献[22]所得分区方案全系统负荷恢复曲线。

图5 39节点系统恢复过程负荷恢复量对比Fig.5 Comparison of load recovery during system restoration process of IEEE39 system

对比曲线4和曲线5、6可知，本文所得子系统分区方案的全系统加权负荷恢复量在所有恢复时段均大于文献[16]和文献[22]方法，由于文献[16]和文献[22]在分区时未考虑各节点的负荷恢复时间，在经过10个时段的恢复过程后，仍有部分负荷未恢复，其中包括节点18所在的重要负荷；而本文算法则实现所有负荷的恢复。

因此，本文模型及算法所得到的分区划分方案各项指标均明显优于文献[16]和文献[22]方法。

3.2 某实际电网

本文继续以包含68个节点，97条线路，22台发电机组的某省500 kV以上网络分区为例，进一步验证所提模型算法的有效性。机组BHP、GBP和NSP为该系统的黑启动电源，其余为被启动电源，节点WXM、JH、FC、HC、PY所在负荷为重要负荷，其余负荷为一般负荷。

本文算法所得到的初始分区结果如图6所示。初始分区经过3次迭代后收敛，最终所得的分区结果如图7所示。为了进行对比和分析，图7中也给出了根据文献[16]和文献[22]方法所得到的子区域划分方案。

图6 某实际电网初始划分方案Fig.6 The initial partition result of some practical power grid

图7 不同方法对于某实际电网的分区方案对比Fig.7 Comparison of partition results of some practical power grid by different methods

由分区方案可以看出3种方法中存在如下两个方面的不同。

1)机组XNP的分区归属不同，在本文分区恢复方案中，机组XNP在时段3从子区2黑启动电源获得启动功率开始启动，而在文献[16]和文献[22]所得分区恢复方案中，XNP在时段5从子区1黑启动电源获得启动功率。

2)负荷RB、FC、CS的分区归属不同，其中FC为重要负荷，在本文所得分区恢复方案中，负荷FC在时段7恢复，而在文献[16]和文献[22]所得分区恢复方案中，FC在时段13恢复。

表2为采用3种方法得到的分区结果，经计算本文各子区功率不平衡量占对应分区机组总发电量的百分数均在合理范围内。

表2 采用3种方法得到的分区不平衡量对比结果Tab.2 Comparison results of unbalanced power by three methods

图8给出了根据本文方法与文献[16]和文献[22]方法所得到的分区进行分区恢复所得到的各个恢复时段系统负荷的恢复情况。因本文曲线4明显高于对比方法曲线5、6，再次证明本文所得子系统分区方案全系统负荷恢复量在所有恢复时段均明显大于文献[16]和文献[22]方法，相应证明本文方法的优越性。

图8 根据不同分区方案的某实际电网恢复过程负荷恢复量对比Fig.8 Comparison of load recovery during system restoration process of some practical power grid by different partition methods

为了进一步验证本文并行算法相对于串行算法的优越性，定义加速比为串行计算时间与分区系统中最大计算时间的比值，表3列出了39节点系统和某实际电网的串行与并行计算时间，由表中的加速比可以看出并行计算可以大大提高计算的效率，且规模越大的系统，并行算法相对于串行算法的优势越大。

表3 系统恢复的串行与并行计算时间Tab.3 Serial and parallel computing time of system recovery

4 结论

针对大停电后的并行恢复分区模型尚不完善问题，本文提出了计及子系统恢复过程影响的最优分区新模型。该模型以分区停电损失及分区间的联络线数目最小为目标函数，以机组归属唯一性、分区功率平衡、分区连通性等为约束；并进而提出了分解求解策略，即把该问题分解为单纯的已知各负荷点恢复时间的分区问题和已知分区的各子系统恢复问题，此时描述该两个子问题的模型均为混合整数线性规划问题，可分别采用CPLEX求解器直接求解，通过两个子问题之间的迭代求解，即可获得原模型的解。多个算例证明了本文模型及求解算法的有效性和正确性。