Churchill-Chu关系式在极薄金属层内传热的适用性研究

李宗洋，常华健,，韩 昆，陈 炼，房芳芳

(1.清华大学 核能与新能源技术研究院，北京 100084；2.国核华清(北京)核电技术研发中心有限公司，北京 102209)

在假想的反应堆严重事故中，如失水事故(LOCA)，堆芯因失去冷却水，使得堆芯升温熔化并落入到压力容器下封头内，形成分层的熔池结构。高温的熔池对压力容器的完整性造成威胁，有可能会使放射性物质泄漏到环境中。堆内熔融物滞留(IVR)通过对压力容器外部进行冷却(ERVC)可将熔融物隔离在压力容器内，避免了放射性物质的泄漏[1-2]。IVR策略最早应用于AP600和VVER-400[3-4]。AP600和AP1000也开展了相应的熔池传热、熔融物滞留研究[5-7]。之后，基于ERVC-IVR思想，开展了许多针对熔池顶部金属层的研究，如MELAD试验[5]和HELM试验[8]。

在分层的熔池结构中，主要有2层和3层熔池结构。在2层熔池结构中，底部是带有衰变功率的氧化物层，而顶部是包含Zr、不锈钢的金属层[6,9]。MASCA试验[10]发现，位于顶部的金属层中Zr会将氧化物层中的重金属U析出，使得U迁移到顶部。由于U的密度较氧化物层的大，因此其最终会落入到下封头底部，逐渐形成1层重金属层。Carénini等[11]的研究指出，这种重金属层的厚度能达到0.4 m。而重金属层的形成将会使顶部的金属层高度降低。熔池结构从上到下可能转为薄金属层、氧化物层和重金属层。

随着薄金属层高度逐渐降低，其侧壁处的热流密度逐渐增大，这会使压力容器壁面的热载荷逐渐加大，热聚焦效应逐渐增强，进而使压力容器有失效的风险。在薄金属层的传热计算中，常用Globe-Dropkin关系式[12]和Churchill-Chu关系式[13]分别计算轴向和径向的传热。在之前的研究中，如MELAD试验和HELM试验，都用到这两个关系式去预测薄金属层内的传热，且预测结果较好。但随着薄金属层高度逐渐降低，Churchill-Chu关系式是否仍适用，还有待进一步验证。随着薄金属层高度逐渐降低至0.15 m以下时，BALI试验[14]发现，计算结果和试验结果偏差逐渐增大，且计算结果较试验结果更大。

在分层的熔池结构中，认为氧化物层底部和顶部因为有冷却边界，因此氧化物层边界处结壳，形成了等温边界。而NUREG[6]计算发现，随着薄金属层高度逐渐降低后，其底部的温度也在逐渐增高，但未超过氧化物层壳层的熔点。NUREG中只给出了0.8～1.0 m之间的计算，对于更低的薄金属层高度，或更高衰变功率的情况并没有给出相应的计算结果。随着反应堆功率的提升，如中国的CAP1400和韩国的APR1400，熔池内的衰变功率也将进一步提高。且随着薄金属层高度逐渐降低，其底部的温度有可能会超过壳层的熔点，进而使等温边界假设失效。等温边界假设失效后的传热过程仍待进一步研究。

本文研究出现假想的反应堆严重事故后，堆芯形成稳定分层熔池结构后的传热情况。通过HELM-LR试验验证Churchill-Chu关系式在极低高径比条件下的适用性，并将Churchill-Chu关系式运用到NUREG的反应堆融毁事故序列分析案例中，研究随着薄金属层高度逐渐降低，侧壁处的热聚焦效应的变化情况，以及氧化物层的等温边界假设在薄金属层高度降低时是否会失效。

1 试验装置

1.1 试验段

HELM-LR的试验段主要由膨胀水箱、上盖板、可改变高度的圆柱桶节、下加热底板和可调节支架构成。圆柱桶节外面和上冷却盖板中布置有冷却流道，可实现对试验段的冷却。上冷却盖板可更换为带有保温材料的盖板，实现对试验段顶部的保温，如图1所示。试验段内径为1.0 m，高度分别为0.16 m(包含3个圆柱桶节0.06 m+0.06 m+0.04 m)、0.10 m(包含2个圆柱桶节0.06 m+0.04 m)和0.04 m(包含1个圆柱桶节)。

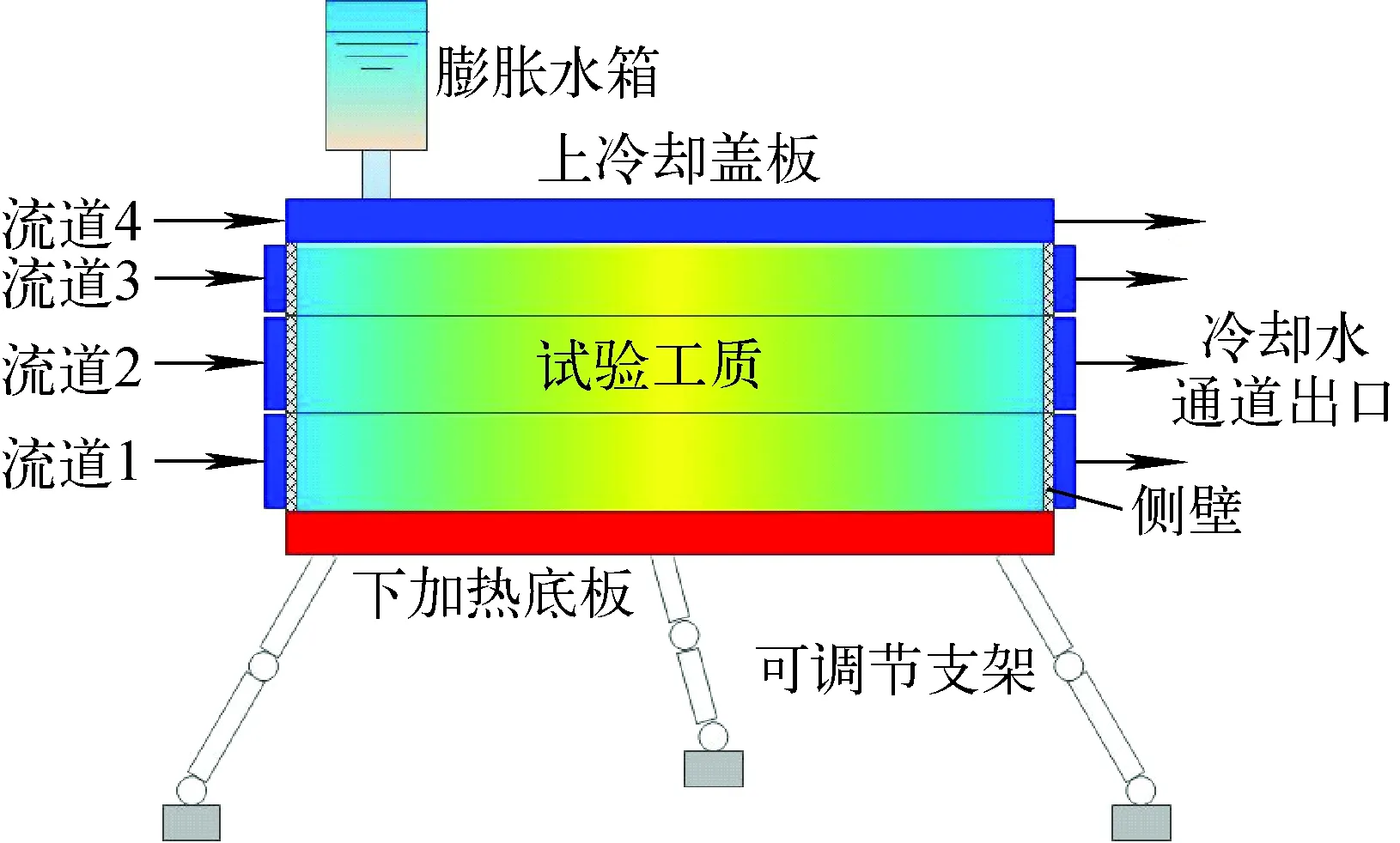
图1 HELM-LR试验装置系统流程图Fig.1 Schematic of HELM-LR experimental apparatus

试验段由底部加热、侧壁冷却，顶部可实现冷却或绝热。下加热底板用来模拟从氧化物层向金属层传递的热量，侧壁冷却通道模拟薄金属层的侧壁冷却边界。这些冷却通道和循环冷却水系统连接，进而提供稳定的冷却水流量和温度。膨胀水箱可确保每次试验时，水都能充满整个试验段。因水作为试验工质具有很好的经济性、适用性，在熔池传热相关试验中广泛使用，所以HELM-LR试验也采用水作为模拟工质。

1.2 温度测量

在上盖板和下加热底板处，分别布置有14个热电偶以监测上、下板的温度。对各测量温度取平均，即可得到上盖板或下加热底板的温度；试验段的内壁面和内部共安装有27个热电偶，以监测不同位置处的温度，如图2所示。此外，在各冷却流道进出口位置也安装热电偶，温度测量误差小于0.1 ℃。在试验开始前，通过计算冷却水带走的热量和输入能量之间的比值，可得热平衡效率约为95%。参考MELAD试验[5]和HELM试验[8]中主流温度选取方法，选取试验段中心位置温度为主流温度。对于高度为0.16 m的试验，选取TE10、TE11和TE12的平均温度为主流温度；对于高度为0.10 m的试验，选取TE10、TE11、TE12、TE19、TE20和TE21的平均温度为主流温度；对于高度为0.04 m的试验，选取TE19、TE20和TE21的平均温度为主流温度。

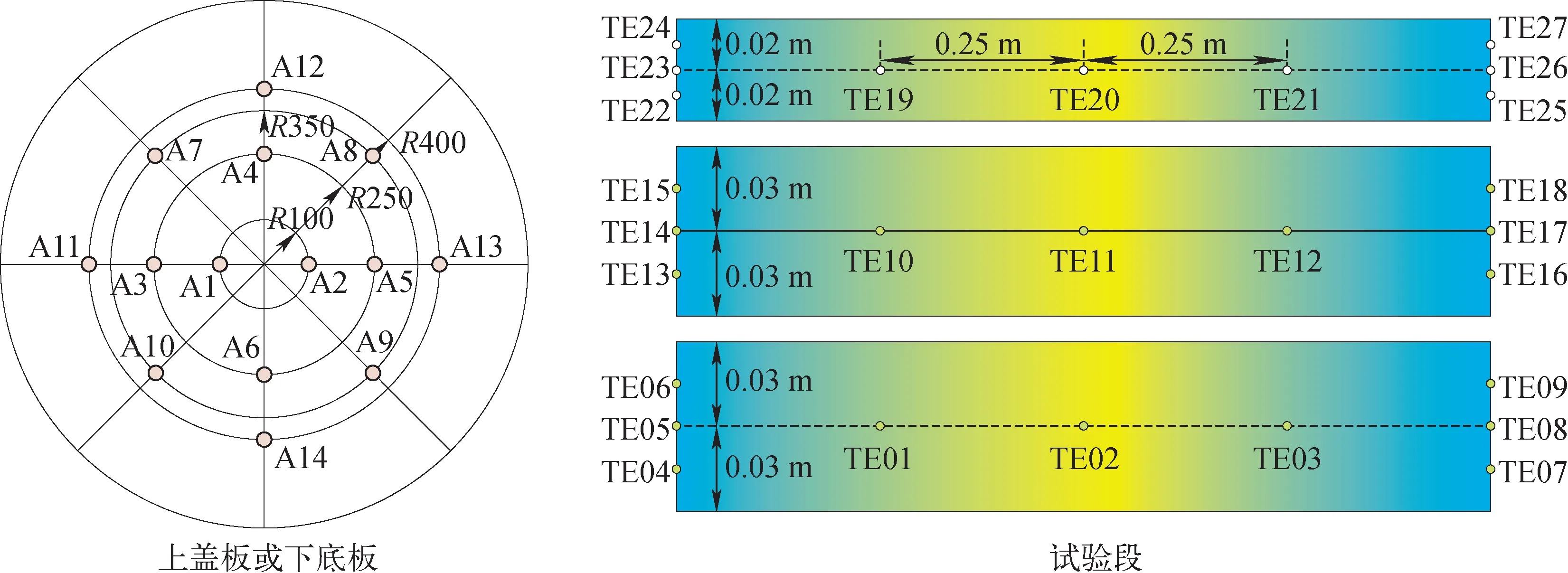
图2 壁面和内部热电偶安装位置示意图Fig.2 Schematic of wall and melt temperature measure points

1.3 关键传热参数计算式

Nu计算式：

(1)

其中：q为热流密度；H为薄金属层高度；λ为导热系数；ΔT为主流温度与顶部或底部的温差。

Ra计算式：

(2)

其中：g为重力加速度；β为热膨胀系数；υ为运动黏度；α为热扩散率。

薄金属层的轴向传热用Globe-Dropkin关系式计算，在MELAD试验[5]中，对Globe-Dropkin关系式进行变换，可得到：

Nu=0.174Ra1/3Pr0.074

(3)

薄金属层的径向传热用Churchill-Chu关系式计算：

(4)

2 结果和分析

2.1 侧向Nu

HELM-LR试验共开展了9个试验工况，包括3次上盖板绝热和侧壁冷却试验工况、6次上盖板和侧壁均冷却试验工况，如图3所示。图中，Test016(Top/Side)表示该试验的金属层高度为0.16 m，且金属层顶部和侧壁的冷却流道都通有冷却水对试验段进行冷却；Test016(Side)则表示该试验的金属层高度为0.16 m，只有金属层侧壁的冷却流道通有冷却水对试验段进行冷却，上冷却盖板更换为保温盖板，金属层顶部则为保温绝热状态。

图3 侧向Nu的HELM-LR试验值和Churchill-Chu关系式计算值比较Fig.3 Comparison of HELM-LR experiment result and Churchill-Chu correlation calculation result

比较HELM-LR试验值和Churchill-Chu关系式计算值可知，Churchill-Chu关系式能较好地预测薄金属层在低高度条件下的Nu，说明Churchill-Chu关系式仍可用于计算薄金属层高度在极低条件下的径向传热。

2.2 Churchill-Chu关系式在HELM-LR试验中的预测

结合Churchill-Chu径向换热关系式和变换后的Globe-Dropkin轴向传热关系式，以及HELM-LR试验参数，来预测HELM-LR试验中的热流密度和温度等热工参数。

从薄金属层中部传递到其顶部的热流密度ql,t为：

ql,t=hl,t(Tl,bulk-Tl,t)

(5)

其中：hl,t为薄金属层向其顶部的换热系数；Tl,bulk为主流温度；Tl,t为表面温度。

从薄金属层中部传递到其侧壁的热流密度ql,w为：

ql,w=hl,w(Tl,bulk-Tl,w)

(6)

其中：hl,w为薄金属层侧向换热系数；Tl,w为侧壁温度。

从薄金属层底部传递到其内部的热流密度ql,b为：

ql,b=hl,b(Tl,b-Tl,bulk)

(7)

其中：hl,b为薄金属层底部向上的换热系数；Tl,b为底部温度。

能量守恒方程为：

ql,bAl,b=ql,tAl,t+ql,wAl,w

(8)

其中，Al,t、Al,w、Al,b分别为薄金属层顶部、侧壁和底部的面积。

式(5)和(7)中的轴向换热系数按照变换后的Globe-Dropkin关系式计算，变换后的Globe-Dropkin关系式在计算轴向传热方面的适用性在MELAD试验中已得到验证。每次计算中，给定每个HELM-LR试验工况的3个条件作为已知参数，即ql,b、Tl,t、Tl,w，通过循环迭代的方式可求得相应的热流密度和温度等参数，计算结果如图4所示。HELM-LR试验的工质为水，因此式(5)～(8)中工质的物性参数均参照水的物性参数。

在薄金属层传热研究中，侧壁热流密度过大会使壁面热载荷过大，热聚焦效应增强，从而造成压力容器有失效风险。而图4中qw的计算值较试验值偏低，说明计算结果还不够保守。在IVR策略设计过程中，如果用到Churchill-Chu关系式和Globe-Dropkin关系式来计算低高径比的薄金属层传热问题时，建议在计算得到的侧壁热流密度基础上乘一个大于1的因子，进而可使设计结果更加保守可靠。根据HELM-LR试验结果，建议在Churchill-Chu关系式计算得到的换热系数基础上乘以1.3，从而使其在IVR设计计算中更加保守。

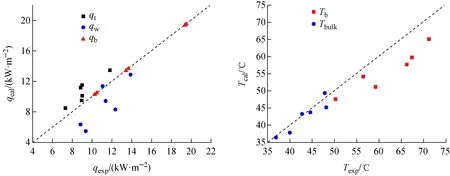
图4 热流密度和温度的计算值和试验值比较Fig.4 Comparison of experiment and calculation values of heat flux and temperature

2.3 Churchill-Chu关系式在IVR中的预测

反应堆出现堆芯融毁事故时，压力容器下封头内逐渐形成了稳定的熔池结构，如图5所示。NUREG研究中用Churchill-Chu关系式计算稳定熔池中的薄金属层径向传热。在NUREG的堆芯融毁案例中，给出了氧化物层衰变功率为1 300 kW/m3时的传热情况，并认为顶部金属层和氧化物层的传热不耦合[6]。但随着反应堆功率的逐渐增大，熔池内的衰变功率也逐渐加大。因此，本文将讨论更大的衰变功率条件对于熔池传热的影响。除氧化物层的内热源外，相应各层的传热方程和物性参数若无特殊说明，均参考NUREG，通过迭代计算可得到相应的计算结果。薄金属层径向传热的换热系数仍用Churchill-Chu关系式计算，但需要在计算时乘以HELM-LR试验得到的放大因子，使计算结果更加保守。

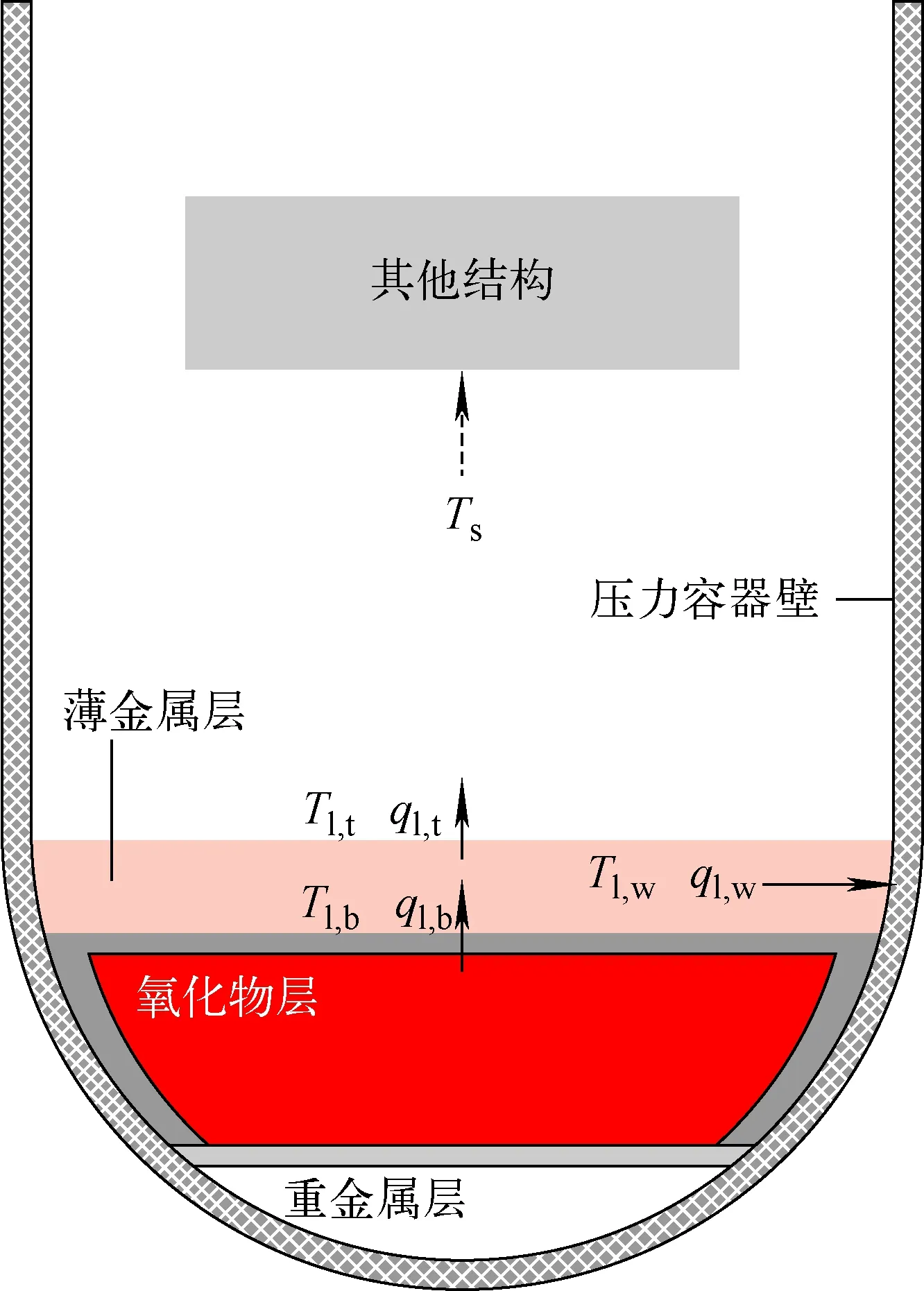
图5 3层熔池结构示意图Fig.5 Schematic of three-layer configuration of molten pool

当氧化物层等温边界假设存在时，氧化物层和薄金属层之间的传热关系式不耦合。在这种不耦合传热关系中，无论薄金属层的高径比为多少，氧化物层内由于等温边界假设的存在，其向上和向侧壁的能量分配比始终保持不变。而在氧化物层等温边界假设失效后，其顶部温度不再是壳层熔点，而是可能随着薄金属层底部温度变化的温度。此时，两者之间的传热耦合，且氧化物层向上和向下的能量分配比不再是确定值。本文旨在研究熔池中薄金属层和氧化物层之间的耦合与非耦合传热计算关系，因此只考虑在不同内热源、不同薄金属层高度下对于熔池内传热的影响。对于RPV壁面的传热和熔化情况均不在本文的研究范围内，故均假设壁面处充分冷却，熔池与RPV壁面接触处都生成了壳层。

1)衰变功率为1 955 kW/m3情况

从薄金属层上表面通过辐射传热传递到吊篮等堆芯其他结构的热流密度ql,t为：

(9)

其中：σ为斯蒂芬-玻尔兹曼常数；Ts为堆芯吊篮等其他结构的温度；As为堆芯吊篮等其他结构的面积；εt和εs分别为薄金属层上表面和堆芯吊篮等其他结构的发射率。

氧化物层内能量守恒方程为：

QoVo=qo,tAo,t+qo,wAo,w

(10)

其中：Qo为氧化物层的体积释热率；Vo为氧化物层的体积；Ao,t和Ao,w分别为氧化物层顶部和侧面的面积；qo,t和qo,w分别为氧化物层向上和向下传递的热流密度。

从氧化物层传递到侧面壳层的热流密度qo,w为：

qo,w=ho,w(To,max-To,melt)

(11)

其中：ho,w为氧化物层侧面的传热系数；To,max和To,melt分别为氧化物层的最大温度和熔点。

从氧化物层向上传递到薄金属层的热流密度qo,t为：

qo,t=ho,t(To,max-To,melt)

(12)

其中，ho,t为氧化物层上部的换热系数。

氧化物层向上传热的换热系数采用UCLA关系式[15]计算：

Nuup=0.403Ra0.226

(13)

氧化物层向下传热的换热系数采用UCLA关系式[15]计算：

Nudn=0.54Ra0.2(H/R)0.25

(14)

在Carénini等[11]的分析中，认为氧化物层的壳层熔点为2 327 ℃(2 600 K)，并给出了从氧化物层传递到薄金属层的热流密度，约为1 000 kW/m2。根据以上传热方程计算可知，对应的氧化物层内热源为1 955 kW/m3。因此选用该条件下的工况作为参考分析。计算结果如图6所示，随着薄金属层高度逐渐降低，其底部温度逐渐升高，但仍低于氧化物层的壳层熔点(2 327 ℃)。此时，氧化物层的壳层等温边界假设仍适用，氧化物层和薄金属层内的传热计算仍不耦合。随着薄金属层高度逐渐降低，侧壁热流密度逐渐增大，侧壁热聚焦效应逐渐增强。该结果和NUREG结果一致。

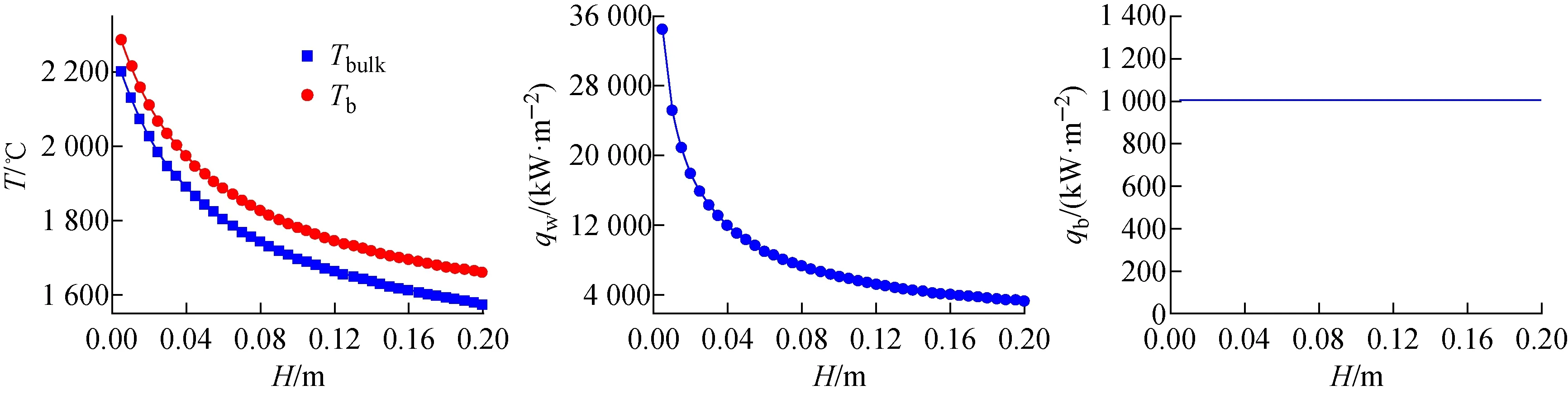
图6 Qo=1 955 kW/m3下不同薄金属层高度对温度和热流密度的影响Fig.6 Effect of different heights of thin metallic layer on temperature and heat flux at Qo=1 955 kW/m3

2)衰变功率为2 500 kW/m3情况

APR1400在出现大破口失水事故(LBLOCA)时，堆芯衰变功率能达到2 500 kW/m3[16]。当衰变功率为2 500 kW/m3且壳层边界假设仍有效时，对应的薄金属层底部热流密度为1 285 kW/m2，此时氧化物层向上和向下的能量分配比为1.28。但当薄金属层高度降低到0.015 m以下时，其底部温度已超过氧化物壳层的熔点。此时，氧化物层顶部壳层熔化，相应的等温边界假设不再适用，需给定新的模型计算向上传热情况，如图7所示。

图7 Qo=2 500 kW/m3下不同薄金属层高度对底部温度和热流密度的影响Fig.7 Effect of different heights of thin metallic layer on bottom temperature and heat flux at Qo=2 500 kW/m3

在不同的严重事故序列条件下，顶部金属层的高度不同。因此，这种顶部金属层极薄条件使得氧化物层的等温边界假设失效是有可能发生的。尤其是在3层熔池形成过程中，重金属层的形成会使薄金属层高度降低。在极端条件下，顶部金属层有可能会全部落入到下封头底部，形成氧化物层在上、金属层在底部的极端情况。

当氧化物层的顶部壳层熔化后，等温边界假设不再适用，其顶部不再是壳层熔点。在之后的计算中，需给定新的计算模型。可认为氧化物层顶部的温度与薄金属层底部的温度相等，将式(12)中的To,melt用Tl,b替换进行新的迭代计算，计算结果如图7a中的红色圆点所示。

考虑等温边界假设不适用时，氧化物层顶部的温度不再是固定的壳层熔点，而是随着薄金属层高度降低而增大的温度，此时薄金属层的传热和氧化物层的传热需要耦合计算，氧化物层向上的传热更难，使得向上传递到薄金属层的热流密度较不考虑等温边界条件时的热流密度更低，如图7b、c所示。同时，也使得考虑壳层熔化后的薄金属层底部温度和侧向的热流密度较假设壳层未熔化的情况(图7a、b中蓝色三角形)更低，但仍呈现增长趋势。考虑氧化物层顶部壳层熔化后，侧向的热聚焦效应仍随着薄金属层高度降低而逐渐加强，该趋势并没有改变。考虑氧化物层顶部壳层熔化，只是减缓了热聚焦效应增长的趋势。

3)无顶部金属层特殊情况

由图7a计算结果可知，随着薄金属层高度逐渐降低，氧化物层顶部的壳层逐渐消失。在这种极端情况下，氧化物层顶部通过辐射的形式向堆芯吊篮等其他结构换热。辐射换热计算方程如下：

(15)

其中，To,t为氧化物层顶部的温度。将式(12)中的To,melt用To,t替换，通过迭代计算可得到此时氧化物层向侧壁传热的热流密度平均值。当只有氧化物层存在时，它对应的向上和向下的能量分配比为1.10。该数值较壳层等温边界假设得到的1.28更低，说明此时通过辐射向上传递的能量更低，向上传热更难。氧化物层顶部存在薄金属层时，有利于氧化物层的热量向上传递，从而减小了氧化物层向侧壁传递能量，使得氧化物层处的侧壁失效风险降低。

而氧化物层最大热流密度在其顶部，根据其热流密度分布关系，在平均值的基础上乘以1.8[11]，即可得到其最大值。图8为不同薄金属层高度对应的薄金属层处RPV壁面的qw-metal和只有氧化物层存在时氧化物层处RPV壁面的qw-oxide最大值的比值，该比值皆大于1。当氧化物层顶部存在的薄金属层厚度较小时，虽然有助于降低氧化物层侧壁处的热流密度，但却增强了薄金属层处的侧壁热聚焦效应，下封头失效的风险增加。因此需要给薄金属层通过进一步注水冷却，从而达到降低薄金属层处的壁面热聚焦效应。

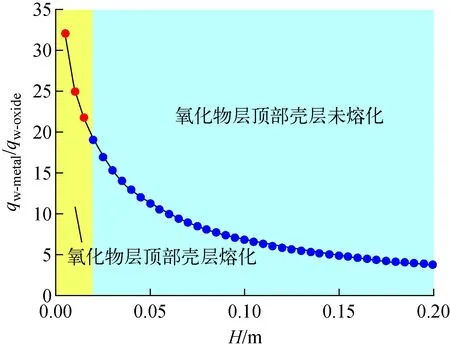
图8 Qo=2 500 kW/m3下不同薄金属层高度对qw-metal/qw-oxide的影响Fig.8 qw-metal/qw-oxide depending on different heights of thin metallic layer at Qo=2 500 kW/m3

3 结论

HELM-LR试验研究了极低高径比条件下薄金属层的传热特性，加深了对IVR策略条件下熔池传热的理解。HELM-LR试验采用水作为试验工质，通过成功开展系列试验研究，获得了有效的试验数据，用以验证Churchill-Chu关系式对于低高径比条件时薄金属层内径向传热计算的适用性，得到如下结论：

1)Churchill-Chu关系式对于低高径比条件下薄金属层径向传热的适用性好，能很好地预测试验结果。HELM-LR试验的侧向热流密度计算值较试验值偏低，使得计算结果更不保守。在IVR策略设计中，应在Churchill-Chu关系式计算得到的侧向热流密度基础上乘一个大于1的因子，从而使得设计结果更加保守。

2)Churchill-Chu关系式能很好地预测薄金属层中的热聚焦效应。

3)当衰变功率密度逐渐升高至2 500 kW/m3，且薄金属层高度逐渐降低至0.015 m以下时，薄金属层底部的温度将会超过氧化物层壳层熔点，氧化物层的等温边界假设失效。通过给定新的氧化物层顶部温度去计算，结果表明当氧化物层顶部的壳层熔化后，氧化物层向上传递的热流密度降低；虽然考虑壳层熔化后的薄金属层的热聚焦效应较不考虑壳层熔化的热聚焦效应弱，但仍会随其高度的降低而逐渐增强。

4)在出现熔池顶部无金属层的极端情况时，氧化物层向上和向下的能量分配比(1.10)较壳层等温边界假设得到的能量分配比(1.28)更低。此时，氧化物层向上传递的能量降低，向侧壁传递的能量增大，RPV壁面热载荷增大。