页岩储层黏土矿物水化膨胀致裂数值模拟研究

金浩增，赵志红，唐鹏程，张 鑫

(1. 西南石油大学 油气藏地质及开发工程国家重点实验室，成都 610500； 2. 中国石化西南油气分公司石油工程技术研究院，四川 德阳 618000； 3. 中国石油新疆油田分公司 工程技术研究院，新疆 克拉玛依 834000)

0 引言

页岩储层属于低孔低渗储层，相对于常规储层，其开发难度较大，为获得较好的产气效果，90%的页岩气井需要通过水力压裂技术对储层进行改造[1]。由于页岩储层黏土含量高，纳米级孔隙和微裂缝层理发育[2-3]，使得页岩储层天然具有极强的吸液能力[4-5]，进而导致页岩压后自然返排率低[6-7]。据一些现场统计显示，页岩气产量与返排率呈负相关关系[8-9]，闷井后产水量降低而产气量增加[10-11]，这主要是由于页岩吸水后对物性产生了重要影响。目前关于吸水对页岩物性参数的影响是否有利尚无一致认识，对页岩气井最终产量的影响尚不明确。因此，研究页岩吸水后对孔隙结构的影响机理对页岩气勘探开发具有重要意义。

国内外学者针对页岩吸水诱导微裂缝方面开展了大量的实验研究，Dehghanpour[12]观察吸水后页岩表面裂缝并分析微裂缝扩展特征；赵向原[13]从地质因素和工程因素分析水化诱导微裂缝的原因；蒙冕模等人[14]利用核磁共振方法分析了页岩吸水微裂缝扩展规律；石秉忠等人[15]使用CT扫描技术分析了诱导裂缝萌生与扩展的规律。YANG等人[16]用基于颗粒填充的离散模型研究由吸水引起的裂纹，当拉伸应力超过拉伸强度时，裂纹将扩展。ZHOU等人[4]认为诱导微裂缝是由于岩石剪切拉张破坏以及黏土水化使得原有裂缝重新张开。BONNELYE等人[17]指出，页岩富含黏土矿物，水相进入页理面与定向排列的黏土矿物发生水化作用，晶格膨胀，产生巨大水化应力，当应力强度因子大于岩石的断裂韧性时，微裂缝开始缓慢扩展。

目前国内外对页岩吸水诱导裂缝的认识分为两类，一是基于Özkaya的椭圆孔受力物理模型或二维平面内一条单裂缝受力建立数学模型；二是页岩吸水后由内部膨胀不均匀而导致的内应力场诱导微裂缝的起裂和扩展，但还没有建立相应的模型。该文以四川盆地龙马溪组页岩为研究对象，根据复合材料理论，建立双组分页岩膨胀模型，分析黏土矿物水化膨胀诱导微裂缝起裂扩展过程，为促进页岩水化诱导微裂缝膨胀提供新思路。

1 页岩水化膨胀致裂模型

1.1 几何模型

页岩细观上是由随机非均质分布的颗粒结合而成的层状矿物，而在组成页岩的众多矿物中仅有黏土矿物与水相接触后会发生物理化学反应，从而引起水化应力场的改变和黏土矿物体积的膨胀。故此，该文建立的模型分为水化膨胀的黏土矿物和石英两相，为了方便计算，将黏土考虑为各向同性膨胀的弹性圆形矿物，其直径d为页岩边长的1/20，这样保证页岩足够大以将场条件表示为无限边界，并通过ABAQUS中的cohesive单元将黏土矿物嵌入到非黏土矿物中。由于黏土矿物吸水后体积膨胀，因此利用温度膨胀来模拟黏土自发吸水膨胀过程。假设样品在z方向上的厚度小于平面尺寸，该几何模型如图1所示。

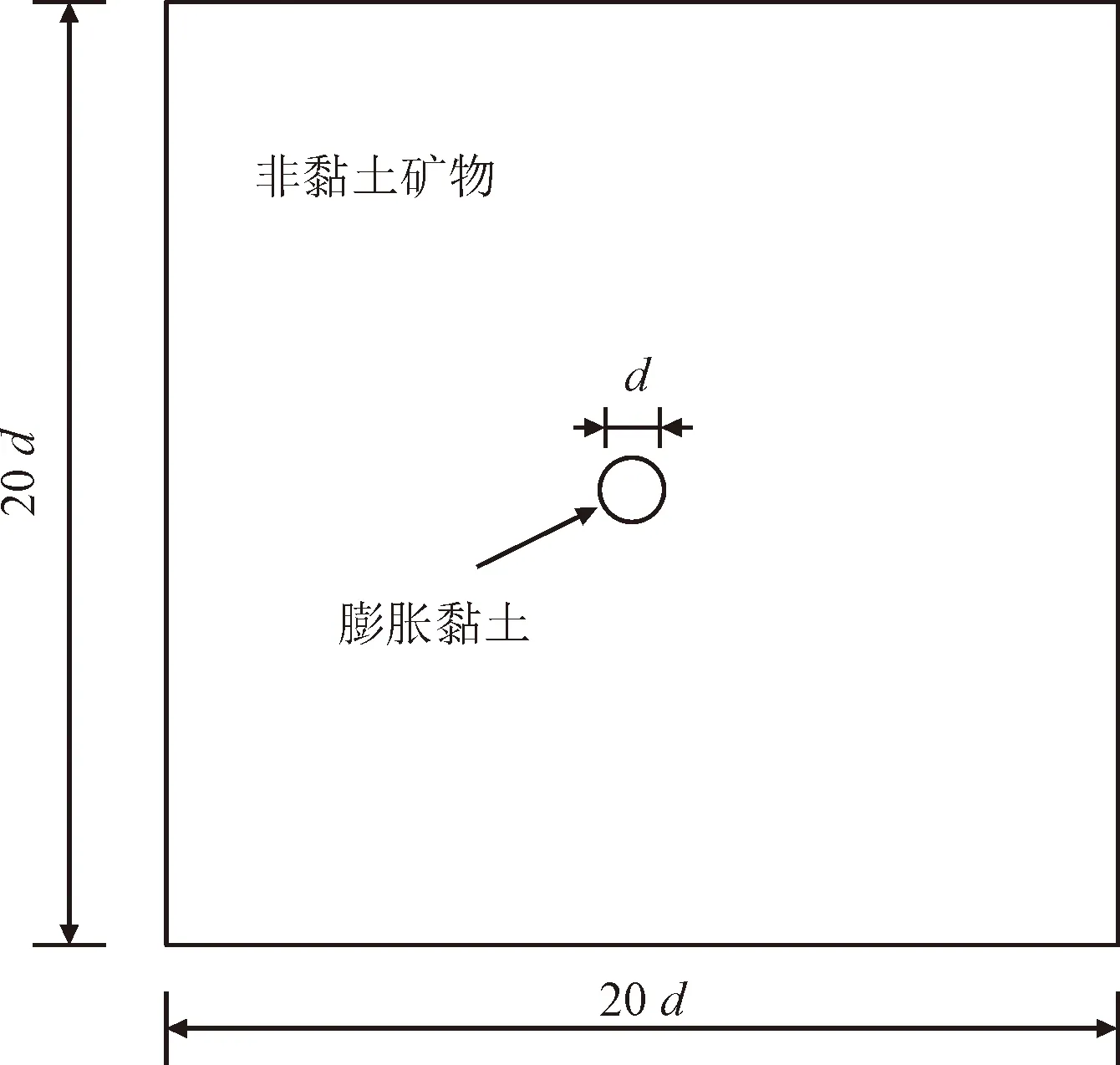
图1 几何模型Fig.1 Geometric model

1.2 双组分页岩模型

假设黏土矿物和石英宏观上是均质各向同性的。对龙马溪组页岩进行单轴抗压强度分析，实验结果表明，龙马溪组页岩单轴抗压强度为40.00～65.30 MPa，平均值为53.38 MPa；杨氏模量为16.05～19.68 GPa，平均为17.73 GPa；泊松比为0.182～0.493，平均为0.313。龙马溪组页岩和石英的部分力学参数如表1所示，从这些参数估计黏土矿物成分的力学参数。

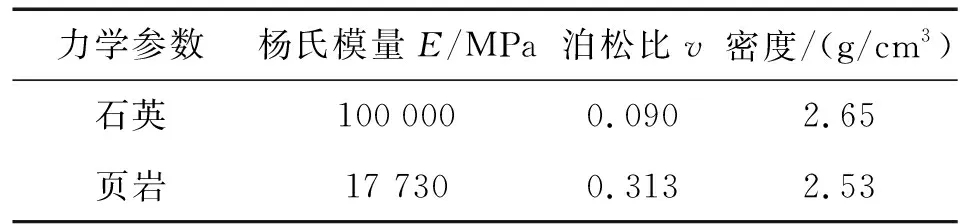
表1 黏土矿物和非黏土矿物的部分力学参数

令页岩总体积分数n为1，那么，石英和黏土矿物的体积分数可以计算如下：

(1)

(2)

(3)

nc=1-nq

(4)

式中：Vsh和Vq分别为页岩中黏土矿物和石英的体积，cm3；nc和nq分别为页岩中黏土矿物和石英的体积分数。

借用复合材料理论[18]，可以使用等应变和等应力模型来估计可接受的黏土矿物的杨氏模量Ec的范围。

对于等应变模型，下界可以计算为：

Esh≤nqEq+ncEc

(5)

对于等应力模型，可以将上限计算为：

(6)

1.3 模型验证分析

由于页岩吸水后，在距离自吸端面不同位置处其含水量不同，则黏土矿物吸水量不同，必将导致其水化膨胀程度不同。依据CHENEVERT[19]实验，硬脆性泥页岩的径向应变最大值为0.5%，所以，为了研究含水量梯度对黏土矿物膨胀的影响情况，假设距离自吸端面的由近及远的黏土矿物的膨胀率分别为0.5%，0.2%和0.1%，且样品在z方向上的厚度小于平面尺寸。因此，该几何模型如图2所示。

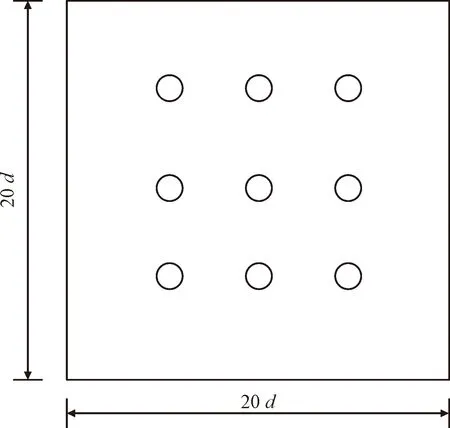
图2 几何模型Fig.2 Geometric model

在模型中，黏土矿物半径为2 μm，杨氏模量为4 000 MPa，泊松比为0.313，膨胀率由近及远分别为0.5%，0.2%和0.1%，地层杨氏模量为17 730 MPa，泊松比为0.20，剪胀角为36.31°，渗透系数为0.667，其他参数如图3所示。

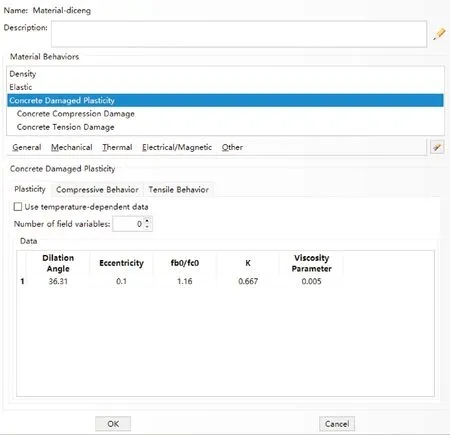
图3 地层参数Fig.3 Formation parameters

模拟结果如图4所示，由图可知，距自吸端面距离越近的地方，由于黏土矿物水化膨胀率高，其诱导的内应力高，微裂缝起裂扩展也更明显；随着自吸时间的增加，页岩孔隙中的水相向前推进，导致微裂缝不断扩展。这与石秉忠[15]用CT观察到的现象一致。图5所示为试样淡水水化5 min自下而上不同位横切面图，从图中可以看出微裂缝不断扩展延伸的整个过程。

图4 模拟结果Fig.4 Simulation results

图5 试样淡水水化5 min自下而上不同位横切面图Fig.5 Cross section of fresh water hydration for 5 min from bottom to top

2 页岩吸水致裂模拟

2.1 计算基本参数

计算参数取自四川盆地龙马溪组页岩，其黏土含量为17.3%～48.1%，平均含量为22.3%，由于该文研究黏土矿物水化膨胀致裂，所以将模型简化为膨胀黏土矿物和非膨胀黏土矿物。取黏土矿物含量为20.0%，则非黏土矿物含量为80.0%，页岩总质量为m=1 g，那么，

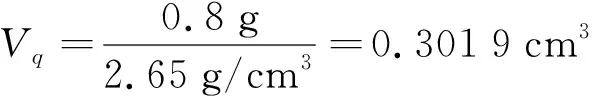
nc=1-nq=0.236 3

将上述数据分别代入式(5)和式(6)，计算黏土矿物的杨氏模量的范围。

对于等应变模型，其杨氏模量下限为：

Esh≤nqEq+ncEc⟹17 730≤0.763 7×100 000+

0.236 3×Ec⟹Ec≥0

对于等应力模型，计算其上限为：

⟹Ec≤484 6 MPa

根据上述结果，确定黏土矿物的杨氏模量Ec为0≤Ec≤ 4 846 MPa。

模型基本参数如表3所示，该文取黏土矿物的杨氏模量为4 000 MPa。

表3 模型基本参数

2.2 单黏土矿物膨胀致裂

几何模型如图6所示, 将页岩考虑为一个弹性圆形黏土矿物嵌入非黏土矿物中, 页岩尺寸为80 μm×80 μm的正方形。该黏土矿物水化导致均匀的各向同性膨胀。黏土矿物选择直径d是页岩边长的1/20，这样页岩足够大以将场条件表示为一无限边界。假设样品在z方向的厚度远小于平面尺寸，因此，该二维模型采用平面应力状态。

图6 几何模型Fig.6 geometric model

在模型中，黏土矿物半径为2 μm，杨氏模量为4 000 MPa，泊松比为0.313，膨胀率0.2%，地层杨氏模量为31 027 MPa，泊松比为0.20，剪胀角为36.31°，渗透系数为0.667，其他参数如图3所示。模拟结果如图7所示。由模拟结果可知，膨胀的黏土矿物与非黏土矿物的相互作用产生了内应力，应力在黏土矿物与非黏土矿物的界面处最大，并随距黏土矿物中心的距离的增大而减小，最大处Mises应力可达40.86 MPa。这与康毅力[20]定量表征的页岩水化微观作用力接近。因此，页岩储层为平衡黏土自吸作用产生的内应力，在黏土矿物与非黏土矿物界面处诱导7条向外延伸的微裂缝。

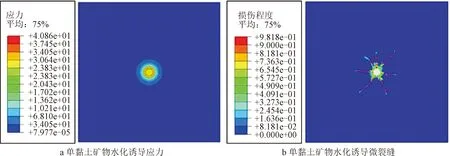
图7 模拟结果Fig.7 Simulation results

2.3 双黏土矿物膨胀致裂

前面的模型涉及单黏土矿物嵌入非黏土矿物中，只考虑了黏土矿物和非黏土矿物的相互作用。然而，页岩的内应力场也受黏土矿物之间相互作用的控制。为了研究这些相互作用，将2个圆形黏土矿物嵌入到非黏土矿物中，页岩尺寸为80 μm×80 μm的正方形。该黏土矿物水化导致均匀的各向同性膨胀，选择黏土矿物直径d是页岩边长的1/20，这样页岩足够大以将场条件表示为一无限边界。假设样品在z方向的厚度远小于平面尺寸，模拟了2个圆形黏土矿物嵌入非黏土矿物的情况，它们总是处于平面应力状态。由于相互作用受黏土矿物之间距离的强烈控制，因此研究了各种D值(2个黏土矿物中心之间的距离)的影响。几何模型如图8所示。

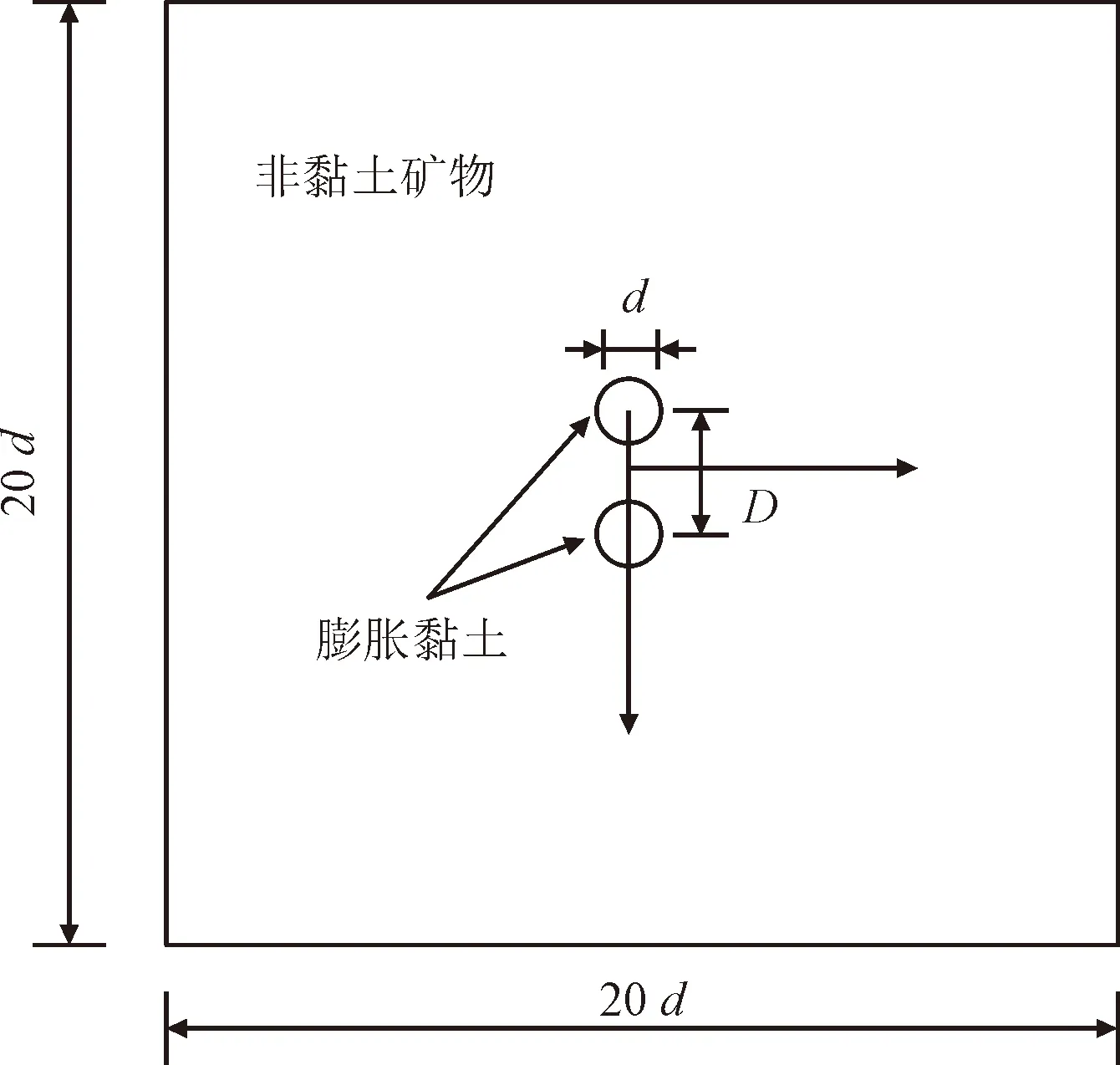
图8 几何模型Fig.8 Geometric model

从模拟结果图9中可以看出, 当2个黏土矿物间距D=2d时, 2个黏土矿物产生的内应力场是对称分布的, 由于膨胀相互挤压导致黏土矿物和非黏土矿物界面处的应力放大，且随着黏土矿物中心距离的增加而降低，最大处Mises应力为47.45 MPa，诱导微裂缝形态为对称双缝。当2个黏土矿物间距离D=3d时(如图10所示)，由于黏土矿物间距离的增加导致应力放大程度减小，最大应力仍出现在黏土矿物与非黏土矿物的界面处，且最大处Mises应力为42.19 MPa，诱导微裂缝形态为对称单缝。当2个黏土矿物之间的距离由D=2d增加到D=4d时(如图11所示)，黏土矿物与非黏土矿物界面处最大Mises应力由47.45 MPa降低到40.81 MPa，与单黏土矿物作用时界面处的应力大致相等，这表明当2个黏土矿物之间的距离D>4d时，由于膨胀互相挤压导致黏土矿物与非黏土矿物界面处的应力放大效应消失。黏土矿物间距离为4d相比于2d和3d时，诱导微裂缝复杂程度较高；相比于单黏土矿物水化诱导微裂缝复杂程度较低，但诱导微裂缝的缝长较长。

图9 模拟结果(D=2d)Fig.9 Simulation results(D=2d)

图10 模拟结果(D=3d)Fig.10 Simulation results(D=3d)

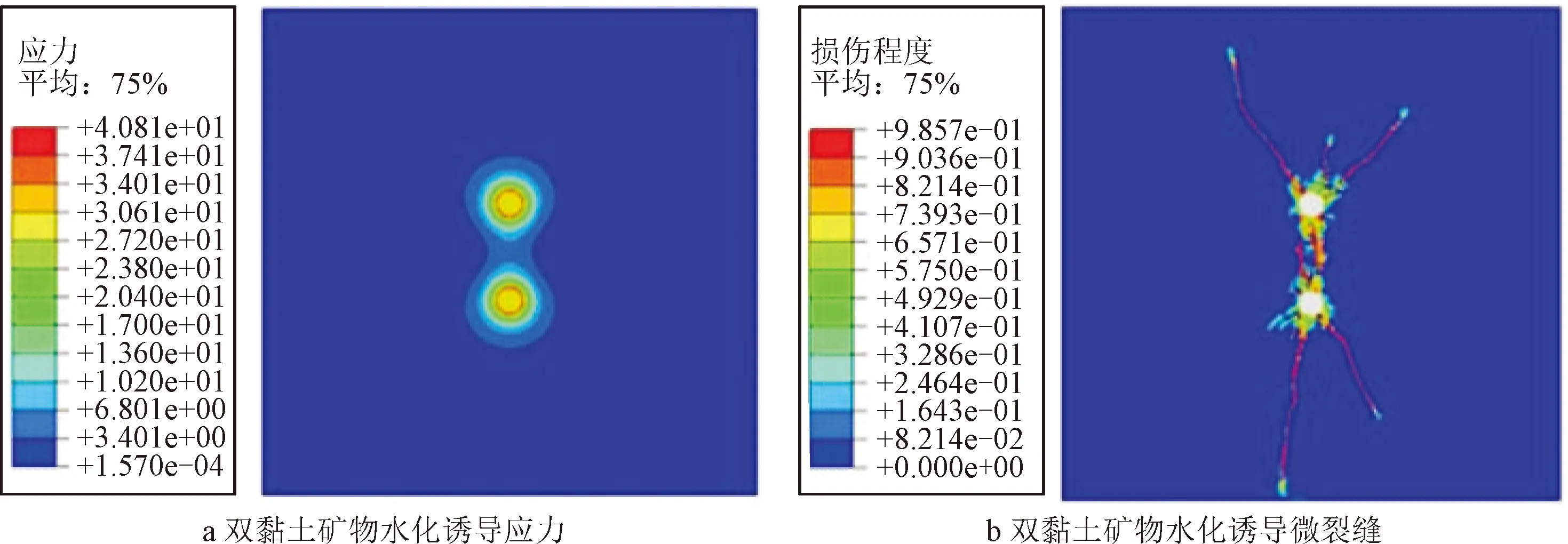
图11 模拟结果(D=4d)Fig.11 Simulation results(D=4d)

3 结论

该文应用复合材料理论的等应力和等应变理论，采用数值模拟方法实现了黏土矿物吸水膨胀后诱导微裂缝扩展的规律研究，得到以下结论：

1)页岩自吸过程中，距自吸端面距离越近的地方，由于黏土矿物水化膨胀率高，其诱导的内应力高，微裂缝起裂扩展也更明显；随着自吸时间的增加，页岩孔隙中的水相向前推进，导致微裂缝不断扩展。

2)黏土矿物吸水膨胀导致内应力场变化, 且这种应力在黏土矿物与非黏土矿物界面处最大, 并随着与黏土矿物中心距离的增加而减小, 页岩储层为平衡内应力的作用在黏土矿物和非黏土矿物界面处诱导微裂缝。2个黏土矿物产生的内应力场是对称分布的，且由于膨胀挤压导致这种应力被放大，当2个黏土矿物间距离D>4d以后, 这种应力放大效应消失。

3)黏土矿物水化诱导微裂缝的复杂程度随着黏土矿物间距离的增加而减小, 当2个黏土矿物间距离为D=2d时, 诱导微裂缝形态为对称双缝；当2个黏土矿物间距离为D=3d时, 诱导微裂缝形态为对称单缝；而当2个黏土矿物间距离为D=4d时, 诱导内应力场与单黏土矿物诱导的内应力场相似, 诱导微裂缝复杂程度较单黏土矿物简单，但是缝长较长。