基于干预模型的酒驾违法查处与事故关联分析*
2022-04-24许卉莹瞿伟斌公安部交通管理科学研究所
许卉莹 瞿伟斌 公安部交通管理科学研究所
引言
世界卫生组织的调查显示:酒后驾驶是车祸致人死亡的一个主要原因。在多数国家,酒驾是导致交通事故的首要原因,例如美国、南非等。在我国目前仍处于酒驾事故的高发期,起数、死亡人数总量比较大,造成了巨大的生命财产损失。据统计,每年酒驾肇事事故超过万起,占到事故总数的6%。近年来,随着查处执法力度的进一步加大,酒驾违法行为大幅减少,酒驾事故也在相应减少。2020年因受疫情影响,酒驾行为的查处稍有减弱,与此相对的,酒驾醉驾事故有所抬头。从近年酒驾违法和事故数据可以看出,酒驾查处力度对于酒驾事故的发生有比较明显的影响,可以通过分析两者之间的关联关系,更加客观的了解交通事故的发生机理,从而为交管部门的管理决策提供数据依据和技术支撑。
一、酒驾违法与事故相关性分析
在酒驾的情况下,驾驶人对外界的反应能力及控制能力下降,导致运动反射神经迟钝、易疲劳等,容易发生事故。而交警查处酒驾,一方面使得饮酒的驾驶人无法继续驾驶,避免事故发生;另一方面会对驾驶人酒驾起到震慑作用,从而达到预防酒驾事故的效果。可以认为,酒驾查处力度和酒驾事故发生之间存在一定的相关关系。
(一)数据集说明
本文以江苏省某城市2018年5月至2020年4月间酒驾违法查处数据与酒驾交通事故数据为例,具体分析其相关性。
从酒驾违法查处情况看,大致分为四个阶段:2018年5月至2019年5月,较为平稳的阶段;2019年6月至12月,因受查处酒驾专项行动影响,酒驾查处数逐月递增,至9月达到峰值,然后稍有回落;2020年1月至2月,因受疫情影响,酒驾违法查处数处于历年最低水平;2020年3月至5月,酒驾违法查处数快速回升,恢复至2019年平均水平。而相对应的,事故数据也分为4个阶段,基本与违法查处时段吻合:2018年5月至2019年5月是上升阶段;2019年6月至2019年9月是下降阶段;2019年10月至2020年1月,酒驾事故数有所回升;2020年1月至2020年5月,该阶段酒驾事故数先大幅下降后快速上升,如图1所示。

(二)相关性分析
相关系数是研究变量之间线性相关程度的量,以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度。本文采用皮尔逊相关系数法,公式如下:

其中,X是酒驾违法查处数,Y事故数。为方便分析,以一周作为时间间隔,将酒驾事故与违法查处数分段计数。以自2018年5月以来每周的酒驾违法查处与酒驾事故数据,计算其相关系数,结果为-0.38,说明两者呈较明显的负相关性。
二、时间序列干预模型建立
时间序列模型可以用于寻找序列值之间相关关系的统计规律,并构建适当的数学模型来描述这种规律,进而利用这个拟合模型来预测序列未来的走势。酒驾事故数据存在明显趋势,符合某种统计规律,可以用时间序列模型来进行预测。而时间序列经常会受到特殊事件及态势的影响,一般称这类外部事件为干预。从上文的相关系数结果来看,酒驾违法查处力度与酒驾事故发生趋势之间具有相关性。提升酒驾违法查处力度,对于酒驾事故的发生来说可以认为是一种特殊干预,可以建立干预分析模型,从定量分析的角度来评估酒驾违法查处力度对酒驾事故的具体影响。具体思路:
(1)利用受干预影响之前的事故数据,建立一个时间序列模型,并利用此模型进行外推预测,得到假设不受干预影响情况下的预测值;
(2)分析预测值与受干预影响的实际值,识别干预效应的形式,确定干预效应函数的参数,构建干预分析时间序列模型;
(3)通过干预分析模型进行事故趋势预测。
(一)酒驾事故受干预影响前的时间序列模型
利用受干预影响之前的酒驾事故数据,建立时间序列模型,预测酒驾事故的发生情况。具体思路:首先识别酒驾事故是否为平稳时间序列,若不为平稳时间序列,则需要对原始序列做平稳化处理;然后再建立差分自回归滑动平均(ARIMA)模型。
1. 数据预处理
数据预处理,就是在建模之前先对原始数据做平稳化处理、白噪声检验和离群值检验,使得处理后的数据满足ARMA模型的假设,为建模做好准备工作。
首先检验序列{Xt}的平稳性。对原始序列做adf检验,当滞后阶数为2时,P值就大于0.1,所以有理由相信序列{Xt} 不为平稳序列,属于非平稳时间序列。然后对序列进行平稳化。使用一阶差分运算后得到一个新序列{Yt} ,Yt=Xt-Xt-1,序列代表每周的环比变化量。在建模之前,还需检验序列是否为白噪声序列。再采用常用的Ljung-Box检验法对新序列{Yt}做随机性检验,检验的结果详见表1。

?
这说明,在0.01的显著水平下,序列{Yt}不为纯随机性序列,即每月的环比变化序列{Yt}是有规律可循的,可以对其建立ARMA模型。
2. 模型识别
模型识别,就是对于给定的时间序列,选取适当的模型阶数p,d,q。在前面预处理过程中,通过一阶差分,将非平稳序列{Xt} 转换为平稳序列{Yt}。因此选定差分阶数d=1。对于平稳序列,识别p,q的主要根据是序列的自相关函数(ACF)和偏自相关函数(PACF)的特征。若序列的偏自相关函数在滞后阶以后截尾,而且它的自相关函数拖尾,则可判断此序列是ARMA(p,0)序列。若序列的自相关函数在滞后q阶以后截尾,而且它的偏自相关函数拖尾,则可判断此序列是ARMA(0,q)序列。若序列的自相关函数、偏相关函数都呈拖尾形态,则此序列是ARMA序列。根据序列{Yt}的样本自相关函数和偏相关函数,初步选定模型的阶数为p=1,q=1。
3. 参数估计
在选定模型阶数之后,对已识别模型中的若干参数进行估计计算。为更准确的选择模型,采用模型的AIC信息检验值进行筛选,根据最小信息量准则选取最优模型,详见表2。

?
将模型修正为ARMA(0,1),得到序列{Yt}的ARMA (2.0)模型,该模型的所有系数估计值都比较显著。
4. 模型诊断
模型的显著性检验即检验残差序列是否为白噪声序列。一个好的拟合模型应该能够提取观察值序列中几乎所有的样本相关信息,即残差序列应该为白噪声序列。反之,如果残差序列为非白噪声序列,那就意味着残差序列中还残留着相关信息未被提取,这就说明拟合模型不够有效。令Xt代表模型对观测值Xt的 估计值(拟合值),定义et=Xt-Xt为拟合残差。采用Ljung-Box检验法对残差序列在自由度分别为6、12、18的情况下做三次白噪声检验,检验结果均显著,可以认为序列{et}为白噪声序列,模型通过模型显著性检验,详见表3。

?
(二)时间序列干预分析模型
1. 模型说明
时间序列干预分析模型可以表示为:

其中,mt代 表干预效应项,它是干预变量的函数,Nt为 ARIMA模型,代表着未受干预影响的基础时间序列。干预变量有多种形式:第一种是持续性的干预变量,可以用阶跃函数式(3)表示;第二种是短暂性的干预变量,用单位脉冲函数式(4)表示。

其中,T为干预时间。干预效应对于模型的影响体现在mt的变化上。当发生持续性干预时,干预效应项可记为m=ωS T,其表示在T时刻发生的干预在经过d个时间单位延迟后干预作用显现;同理当短暂性干预发生时,干预效应项可记为表示T时刻发生的干预在该时刻瞬间对模型产生了ω的影响。
干预效应除了有一定的延迟,同时还可能与自身有一定的相关性,或者干预的强弱也有可能随时间而变化,所以在实际问题中需要将以上基本形式结合起来,对干预效应建模。
2. 建模过程描述
酒驾违法查处行动是非连续且有梯度的干扰,不像简单持续性干扰一样一次行动便始终维持,也不像短暂性干扰只对序列作用一次。在假定酒驾人群比例在短时间内不会改变的前提下,酒驾查处力度与酒驾违法查处数呈正相关。酒驾违法查处数越多,象征着酒驾查处力度越大。一段时间内酒驾查处力度的直接体现就是酒驾违法的查处数量。将TT时间的酒驾查处力度记为ωT, 干预模型如下:

其中,xt为 时间序列的干预项,ηt为去除干预项的ARIMA时间序列模型。
3. 模型诊断
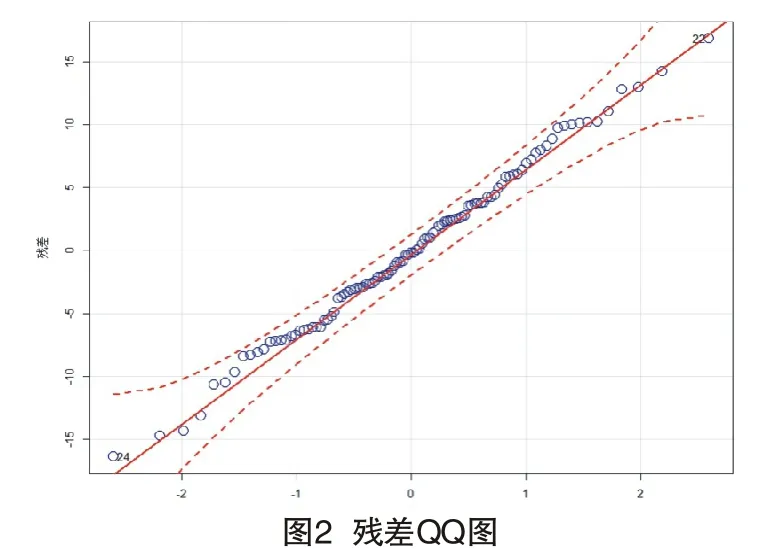
为诊断模型的有效性,需要对模型残差进行检验,通过分析其是否服从正态分布以及是否为白噪声来判断模型是否显著。如图2所示,其残差服从正态分布。采用LjungBox 检验法对上述模型的残差序列{et}做模型显著性检验,检验的结果详见表4,残差序列为白噪声序列的可能性大于99%,模型通过显著性检验。

?
三、模型应用
(一)酒驾事故受干预影响前的时间序列模型应用
从前文数据集的时间特征可知,2019年6月至12月是查处酒驾专项行动影响时段。因此笔者采用2018年5月-2019年5月间酒驾违法查处数据与酒驾交通事故数据,建立受干预影响之前的时间序列模型,并预测2019年6月至2019年9月的酒驾事故数据。预测结果如图3所示,其中实线为实际每周发生的酒驾事故数,虚线为模型预测的酒驾事故数,灰色区域为95%置信区间。根据模型结果来看,在未受干预影响的情况下,序列呈现一个平稳波动的趋势,当前一周的数据与前一周相关,与更早的历史数据关系不大。模型预测2019年6月至9月每周的酒驾事故数应在35附近波动,其95%的置信区间为[21,48]。

(二)干预分析模型应用
将受干预影响前的时间序列模型的预测结果与实际数据进行对比发现,酒驾事故数量自2019年6月以来呈现下降趋势,并且持续位于预测值置信区间以外。可以认为因2019年6月查处酒驾专项行动,酒驾查处力度加大,对酒驾事故数产生了干预影响。接下来将通过干预分析模型来分析具体干预影响的程度。
首先利用kmeans方法将某城市酒驾违法查处数量进行划分,酒驾违法查处数量最高时段的查处力度标记为3,次高的时段标记为2,以此类推,最少的时段的查处力度标记为0。具体划分结果详见表5。

?
然后,基于现有数据集进行参数估计,模型的数学表达式如下:

模型的拟合结果如图4所示。其中红色实线为模型的拟合结果,两条蓝色虚线间的范围为模型置信区间。可以看到,在置信区间下,对于数据的拟合较为符合。

图4 干预模型拟合
通过模型对2020年6月以后的三个月数据进行预测,结果如图5所示,当保持违法查处力度为0时,酒驾事故将维持原有水平;当查处力度为1时,酒驾事故相比原有水平下降8.57%;当违法查处力度为2时,酒驾事故相比原有水平下降17.14%;当违法查处力度为3时,酒驾事故相比原有水平下降28.57%。以上分析说明酒驾查处力度对酒驾事故发生有干预影响。在酒驾查处力度加大时,酒驾事故有下降的趋势。

四、结语
通过建立干预分析模型发现,酒驾违法查处力度对于事故发生的干预效用明显。干预模型能够用来定量分析交通违法行为查处力度对交通事故的干预影响,明确优化执勤执法排班、调整执法力度对事故的干预影响程度,进而可以应用于交通事故预防效果评估、事故趋势预测,为有效预防酒驾事故提供技术支撑。
研究重点在干预模型的建立与分析,而在酒驾违法与酒驾事故数据相关性方面,仅进行了初步探讨,在未来需要进行深入研究。
