利用X-Bar & R chart控制图对混凝土强度波动控制的讨论
2022-04-24李庚
李庚
(信阳市新县月华加工有限公司,河南 信阳 464000)
统计过程控制(Statistical Process Control,简称SPC),指应用统计分析技术对生产过程进行实时监控,科学地区分出生产过程中产品质量的随机波动与异常波动,从而对生产过程的异常趋势提出预警,以便生产管理人员及时采取措施,消除异常,恢复过程的稳定,从而达到提高和控制质量的目的。SPC 管制图建立在数理统计学的基础上,是由美国贝尔电话公司休哈特工程师发明的一种非常实用的管制方法,他把统计学中的“发现异常”作为控制生产过程中的一种工具。因此,“发现异常”成为 SPC 管制图的基础。它利用有效数据建立管制界限,一般分上管制限(UCL)和下管制限(LCL),上管制限通常设为管制中心线 CL+3σ,σ 为标准偏差,下管制限设为 CL-3σ。如果该过程不受系统原因影响,那么,得到的观测数据将不会超出管制界限。强度波动控制主要以平均值与移动极差的波动折线图加上几条水平控制线来分析需要控制的参数的波动情况。控制线与正态分布的关系见图 2。

图1 控制线与正态分布的关系
首先了解一下与 SPC 相关的几个重要的概念:
(1)变差
任何一个工厂,无论其多么先进,从其生产线出来的同一种产品或多或少总会存在一些差异,这种差异就是变差。
(2)普通原因和特殊原因
导致普遍的、固有的、可接受的变差的原因,叫做普通原因。
若不再是常见的、普通的变差,而是有某种特殊原因导致的变差,比如员工的操作的失误,我们把导致这种非普遍的、非固有的、异常的变差的原因叫做特殊原因。
(3)受控和不受控
如果一个过程仅仅只有普通原因引起的变差,我们就说这个过程受控,如果一个过程存在特殊原因引起的变差,我们就说这个过程不受控。
控制图的使命就是帮助我们发现并消除导致过程变异的特殊原因,这是一个使过程从不受控变成受控的过程。
(4)中心极限定理
中心极限定理是 SPC 的重要理论依据。
这个定理是这样的:“设 X1,X2,...,Xn为 n 个相互独立同分布随机变量,其总体的分布未知,但其均值和方差都存在,当样本容量足够大时,样本均值的分布将趋近于正态分布”。
样本容量与正态分布的关系见图 2。

图2 样本容量与正态分布的关系
(5)合理的抽样
抽样就是从研究总体中选取一部分代表性样本的方法。
合理抽样涉及到几个问题:样本大小、抽样频率、抽样类型(连续取样、随机取样或其他结构化取样)。抽样大小(子组大小)会影响控制图的敏感度,样本越大能探测到的均值偏移越小。一般来说,混凝土的强度可以度量,计量取样优于计数取量,我们采用计量型。计量型数据中最常用的是 X-Bar & R chart(均值—极差控制图)。
(6)控制图综合观察
控制图所反应的是“过程”的变化。生产的过程输入的要项为 5M1E(人、机、料、法、环、量),5M1E 的任何变化都可能对生产出来的产品造成影响。换句话说,如果产品的变差过大,那是由 5M1E 其中的一项或多项变动所引起的。如果这些变动会引起产品平均值或产品变差较大的变化,那么,这些变化就会在X-Bar & R chart 上反映出来,我们通过查找管制图中记录的重大事项就可以明了。
1 建立管制界限的条件
1.1 标准差的预估
利用鲍罗米强度经验式以误差传递的方法推导出标准差:

式中:
σ——标准差;
f——混凝土强度;
CVc——水泥强度误差变异系数;
CVt——试验误差变异系数;
CVc/w——胶水比误差变异系数;
m——一组试模的试块数量;
a, b——影响系数;
C——水泥强度。
其中 CVc/w是由水泥用量变异系数和用水量变异系数共同组成,水泥用量误差即水泥称量误差,用水量的误差除了水的称量误差外,还有其他很多因素,所以搅拌站主要控制的是用水量的误差。
CVc/w、CVc、CVt、三者中 CVt最小,CVc次之,CVc/w最大,按照公式做出了控制水平优秀、良好和普通三个等级,利用这三个等级分别求出了不同的标准差。如表 1。
从表 1 中可以看出:随着控制水平的逐渐降低,标准差 σ 越来越大。相应可以求出混凝土强度的变异系数 CV = σ/f,代入公式 (1),已知混凝土强度的截距 B(混凝土强度回归后的截距 B),一组试件 m=3,以及 CVc、CVt和 CVc/w的上限值,代入式 (1),得到了不同强度等级的标准差与变异系数 CV(上限值)图(图3),不同控制水平的条件见表 2。

表1 三个不同控制水平的标准差

表2 不同控制水平的条件
从图 3 可以看出,标准差随着混凝土强度等级变大从接近 0 开始逐渐变大,变异系数随着强度等级变大从无穷大逐渐变小。
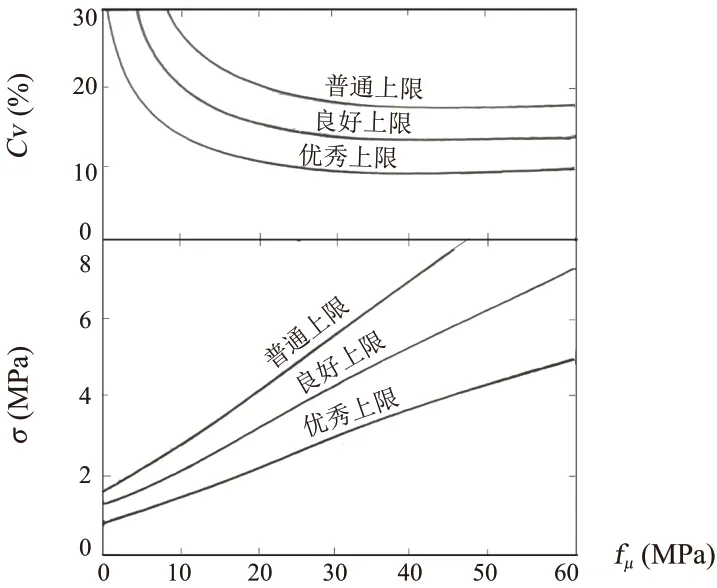
图3 不同强度等级的标准差与变异系数
1.2 试件组数 n 与概率度
随机抽样必然存在客观与主观因素影响,当试件组数 n 足够多,这种误差影响才会降低。根据中心极限理论,当样本容量足够大时,样本均值的分布将趋近于正态分布,客观与主观因素影响正态分布曲线集中分布正态分布的左右边,对概率度造成影响。根据不同结构不同试件组数 n 得到的概率度统计表见表 3。
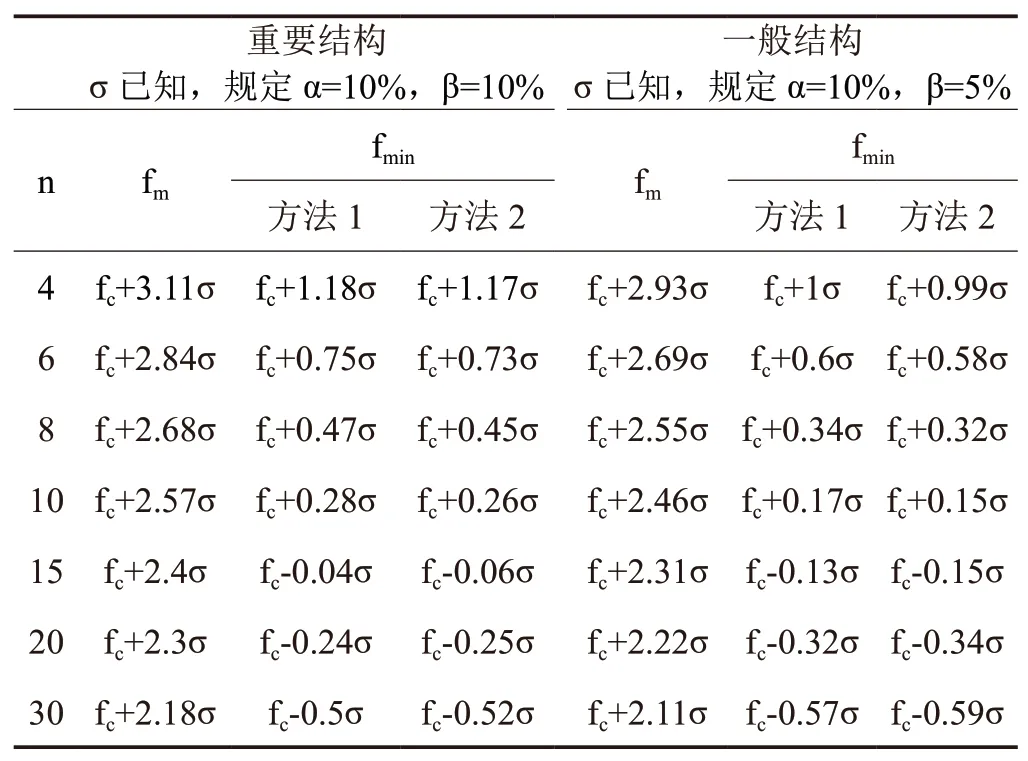
表3 不同结构不同试件组数 n 得到的概率度统计表
本文只讨论方法 1。方法 1 按样本最小值随样本容量增大而减小的统计规律确定。
对于 n 的选择可以根据实际情况选择,在这里我们取 n=30。
1.3 预测强度均值(配制强度)
由于混凝土强度的变异性和抽样的随机性,抽样必然对试件强度有影响,影响因素有试件组数 n 和两类错误 α 和 β。α 为抽样检验的第一类错误,生产方损失,把低于验收强度 fa的错判为不合格,α 一般取 10%;β为第二类错误,使用方风险,将不合格漏判为合格。β 根据工程施工养护情况可以取 5% 和 10%,要求两类错误越小,则配制强度越高,允许两类错误越大,则配制强度越小。根据图 4 确定了预测强度均值的计算公式(式 (2))。根据工程类型和混凝土强度等级、试件组数 n,以及两类错误 α 和 β 的取值,可以求得配制强度。
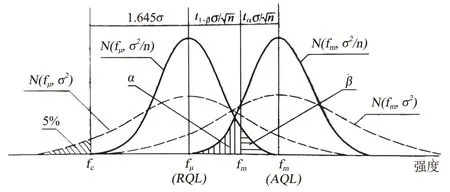
图4 试件强度平均值的验收强度 fa配制强度 fm 的确定方法图示

2 X-Bar & R chart 控制图
在这里不分析标准差很大的情况,只分析标准差最小的情况。根据 GB 50164—2011《混凝土质量控制标准》,C35 选取最小标准差 3.5MPa。
(1)C35 混凝土的 28 天强度 30 组数据见表 4。

表4 30 组混凝土的 28 天强度统计表 MPa
由表 3 得:预期强度为 35+2.18×3.5=42.6(MPa),再算出上控制线为:42.6+3×3.5=53.1(MPa),下控制线为:42.6-3×3.5=32.1(MPa),上警戒线为 42.6+2×3.5=49.6(MPa),合格下限为 35-0.5×3.5= 33.25(MPa),实际平均值为 42.8MPa,实际标准差为 2.5MPa。根据表 4及算出的线值作图,见图 5。
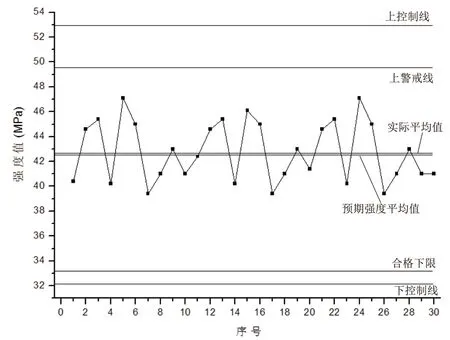
图5 C35 混凝土强度控制图
从图 5 明显可以看出预测强度平均值与实际强度平均值距离相不大,但是预估强度平均值在实际强度平均值下面,说明有普通原因导致的变差,还是处于受控状态。
(2)假如表 4 强度数据是 C30 混凝土 28 天强度,预估标准差为 3.5MPa,由式(2) 得:预估强度平均值为 37.4MPa,再算出上控制线为 47.9MPa,下控制线为26.9MPa,上警戒线为 44.4MPa,合格下限为 28.25。作图见图 6。

图6 C30 混凝土强度控制图
从图 6 明显可以看出预测强度平均值在实际强度平均值之下,而且距离相差很大,部分已经超出了上警戒线。这是由特殊原因造成的失控状态,例如砂含水测量偏高,水泥强度测量偏低,外加剂多计量。
(3)假如表 4 强度数据是 C45 混凝土 28 天强度,预估标准差为 3.5MPa,由式 (2) 得:预估强度平均值为 52.4MPa,上控制线为 62.9MPa,下控制线为 41.9MPa,上警戒线为 59.4MPa,合格下限为43.25MPa。作图见图 7。
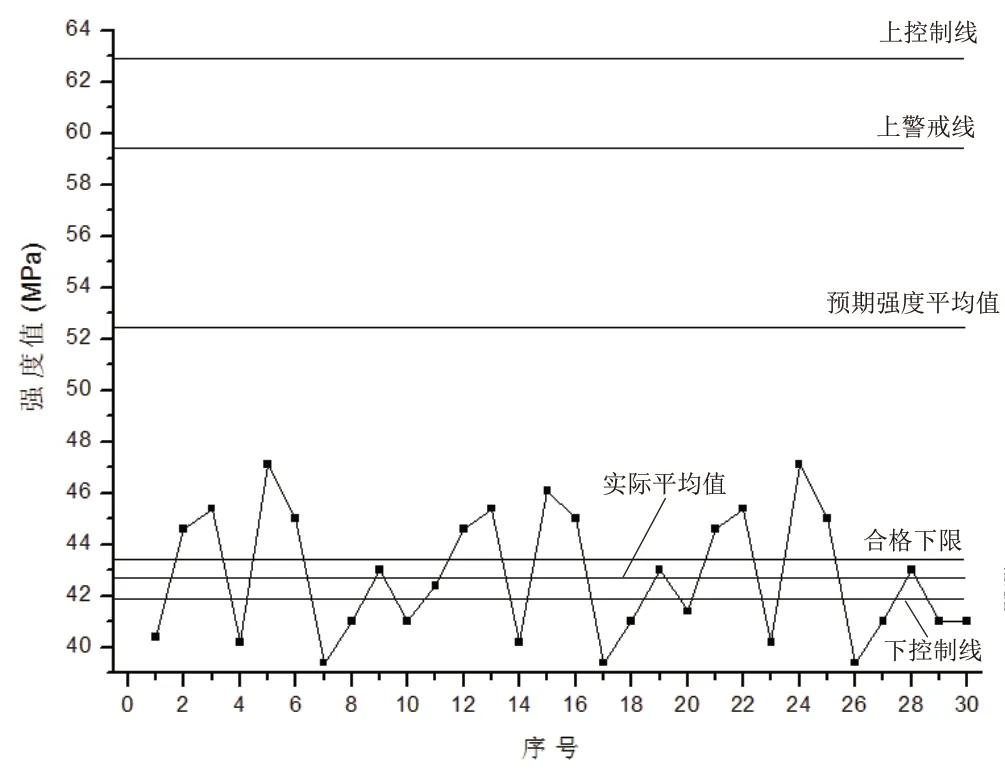
图7 C45 混凝土强度控制图
从图 7 明显可以看出预测强度平均值在实际强度平均值之上,而且距离相差较远,并达到了合格下线边缘,说明砂含水测量偏低,水称计量出错,操作加水,砂含泥量增大等问题,处于失控状态,继续下去会造成安全质量事故。
控制水平普通,选取标准差 σ=5MPa,同样的强度数据,如图 8 所示,预测强度平均值在实际强度平均值之上,距离相差不远,说明控制水平良好。

图8 标准差为 5 的 C35 混凝土强度控制图
移动极差 Rs 数据详见表 5。通过移动极差明显可以看出每个值之间的波动情况(图 9)。移动极差平均值为 2.1。移动极差没有最低值,但限制上限值,我们需要做的就是不能超过上警戒线。
3 结语
混凝土的强度波动可以用 X-Bar & R chart 控制图,三条线与预测均值的比较,方便明了,直观反映控制水平。对于强度的预警作用非常明显。在实施时主要做好标准差、概率度和配制强度的准确把握。

表5 移动极差表 MPa

图9 移动极差波动图
