风西湖相复杂混积岩储层矿物组分及孔隙度计算方法

陈文安,李纲,郭正权,谢琳,刘国良,李贵梅

(中国石油青海油田公司勘探开发研究院,甘肃敦煌736202)

0 引 言

风西地区位于柴达木盆地西部坳陷区大风山构造带西段,N1—N21时期为浅湖—半深湖沉积环境,发育灰云坪、藻席及砂坝沉积微相,储层岩性以碳酸盐岩为主、混杂陆源碎屑及泥质,具有明显的混积特征。根据成因类型和沉积机制将碳酸盐岩归纳为生物成因、物理化学复合成因2大类,结合成分和结构特征,有效储层细分为藻灰岩和灰云岩这2类碳酸盐岩。藻灰岩碳酸盐含量通常大于60%,在弱水动力条件下,藻呈水平纹层状或波状生长,通过早期固结作用形成藻架孔。在高能环境中,由藻体分泌的黏液不断捕集黏结灰泥形成藻团块,呈不规则的多边形或团块状,胶结程度较低,内部碎屑物、泥质含量较高,压实作用使得藻团块紧密相接,团块之间易发生淡水淋溶,形成藻格架次生溶孔,溶孔发育,但藻团块自身几乎不溶解[1]。灰云岩碳酸盐含量在30%～86%,形成于低能环境,几乎全由颗粒直径为0.001～0.004 mm的灰泥组成,含陆源碎屑与石膏,孔隙主要为白云石晶间孔加少量微裂缝。有效储层孔隙度分布在5.0%～15.0%,平均为7.6%,中值为6.6%,60.4%的样品渗透率小于0.02 mD(1)非法定计量单位,1 mD=9.87×10-4 μm2,下同,属特低孔隙度特低渗透率型储层。储层孔喉结构复杂,藻灰岩与灰云岩孔喉结构差异大,藻灰岩平均孔喉半径为224.4 nm,灰云岩平均孔喉半径为86.3 nm,相比较而言藻灰岩的孔喉结构好、渗透性更优。

由于多种因素的相互干扰,湖相复杂混积岩储层定量评价遇到困难,为有效、有针对性地解决这些复杂问题,形成了将岩性扫描、高分辨率电成像、核磁共振与常规资料结合的精细储层评价方法。岩心X衍射及岩心孔隙度资料表明,风西湖相复杂混积岩储层岩性控制物性的特征明显,有效储层的孔隙度与碳酸盐含量呈正相关,与黏土含量、砂质含量呈负相关。岩性扫描测井可以准确确定地层矿物组分[2],核磁共振测井能提供储层测井评价所需要的基本参数,如总孔隙度、有效孔隙度、可动流体孔隙度等。但对于未进行岩性扫描和核磁共振测井的井,要准确确定储层矿物组分及孔隙度,需要其它的可替代方法。本文通过储层参数影响因素分析、岩心标定,与理论模型结合形成了利用常规测井资料计算储层矿物组分和孔隙度的新方法,解决了只有常规测井资料时储层评价所面临的困难。

1 矿物组分计算方法

风西湖相复杂混积岩储层矿物组分复杂,包括白云石、方解石、石英、长石、伊利石、黄铁矿、石膏等。面对如此多的矿物组分,可以利用岩性扫描测井基于元素测量反演地层的矿物组分,但利用常规测井系列很难实现矿物组分的准确定量计算。因此,将复杂混积岩储层矿物组分合并简化为碳酸盐、砂质及黏土这3种组分。

通过敏感性分析发现,储层自然伽马、声波时差、中子孔隙度与矿物组分关系密切,相关性较好,能较好地体现岩性差异。为消除不同井各测井系列本身可能存在的系统差异,降低由平面上存在埋深、构造等因素导致的岩性评价系统误差,提高常规测井曲线计算矿物组分含量的精度,故把校正后的测井曲线进行归一化处理[见式(1)、式(2)、式(3)],并转换为相对曲线,选择N21地层横向对比显示全区稳定性好的Ⅲ-Ⅳ砂组为标准层。

ACp=AC/AC0

(1)

CNLp=CNL/CNL0

(2)

GRp=GR/GR0

(3)

式中,ACp为声波时差归一化后的值;AC为声波时差,μs/m;AC0为标准层声波时差峰值,μs/m;CNLp为中子孔隙度归一化后的值;CNL为中子孔隙度,%;CNL0为标准层中子孔隙度峰值,%;GRp为自然伽马归一化后的值;GR为自然伽马,API;GR0为标准层自然伽马峰值,API。

对测井曲线进行归一化处理的目的是有效提高矿物组分含量的求取精度,归一化后的曲线不应用于孔隙度等物性参数的计算。储层黏土含量、碳酸盐含量以X衍射分析及岩性扫描测井资料为依据,建立解释模型。黏土含量计算模型见式(4),碳酸盐含量计算模型见式(5)。

Vsh=-26.3807+40.8026GRp+

20.0984CNLp-1.5194GRp×CNLp

(4)

Vca=142.3371-59.2026GRp-

35.8392ACp-5.0606GRp×ACp

(5)

式中,Vsh为黏土含量,%;Vca为碳酸盐含量,%。

利用上述模型计算的黏土含量和碳酸盐含量与岩性扫描测井和X衍射实验结果具有较好的一致性,表明计算模型可靠(见图1)。

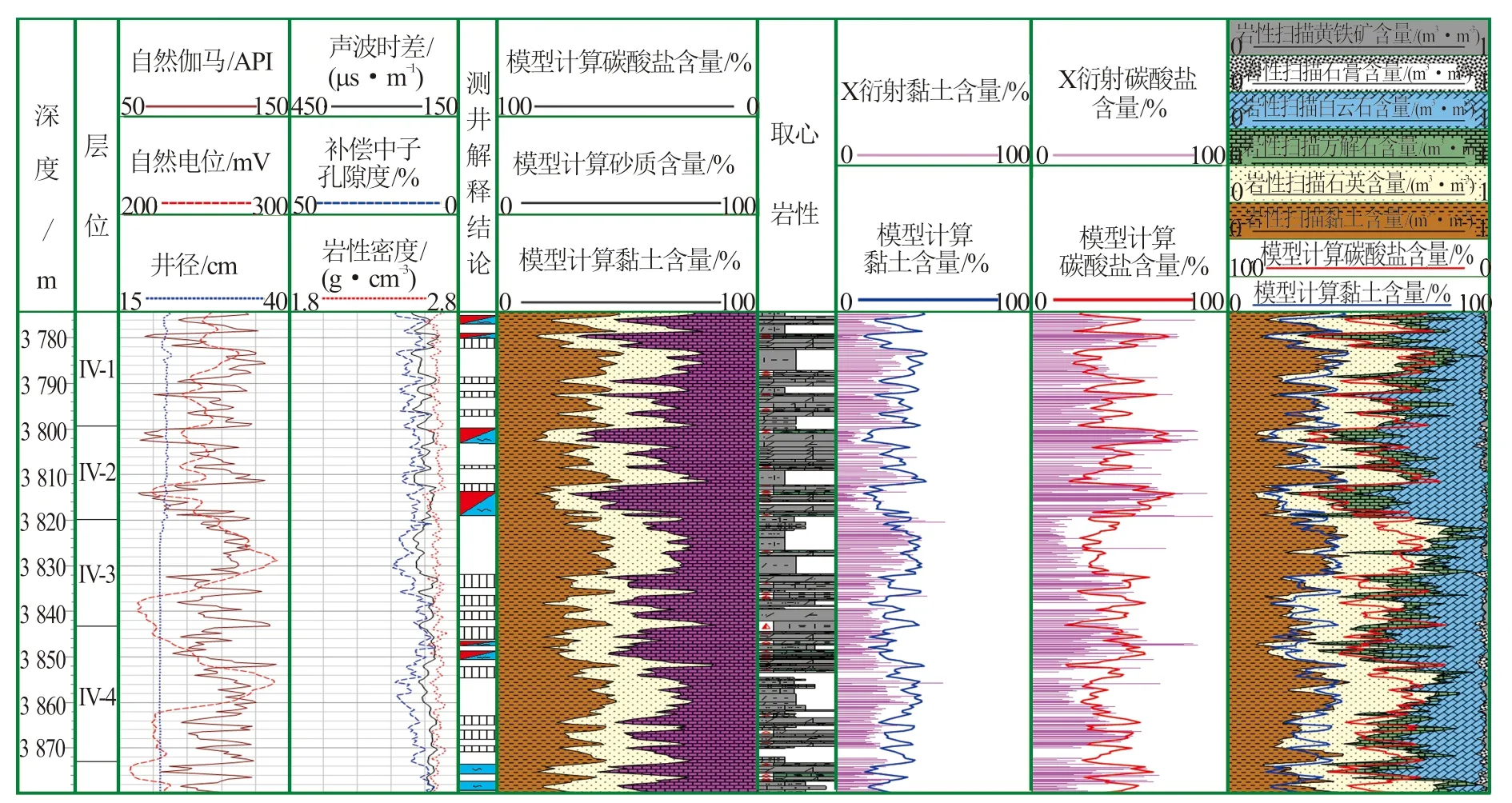
图1 风西X-3井矿物组分计算模型解释剖面验证

2 孔隙度计算方法

2.1 总孔隙度计算模型

2.1.1总孔隙度计算模型的建立

选用92个层段的样品,利用岩心分析孔隙度与岩性密度得到岩心刻度密度模型

φ=-69.272ρ+189.78

(6)

式中,φ为孔隙度,%;ρ为岩性密度,g/cm3。根据式(6)得到的相关系数为0.900 8。

2.1.2岩心刻度密度模型样本层段的矿物组分代表性分析

岩心刻度密度模型代表了储层孔隙度与岩性密度经验统计关系,可以较好地体现储层孔隙度情况,但模型中应用的岩心样本数据大多来源于灰云岩、泥质灰云岩等岩样,高碳酸盐含量的储层样品数量较少。依据岩心X衍射资料,样本层段的碳酸盐岩含量平均为42.3%、黏土含量平均为26.6%、砂质含量平均为25.2%,即建立的岩心刻度密度模型样本层段的岩石骨架值与上述矿物组分匹配的骨架值相当(见表1)。

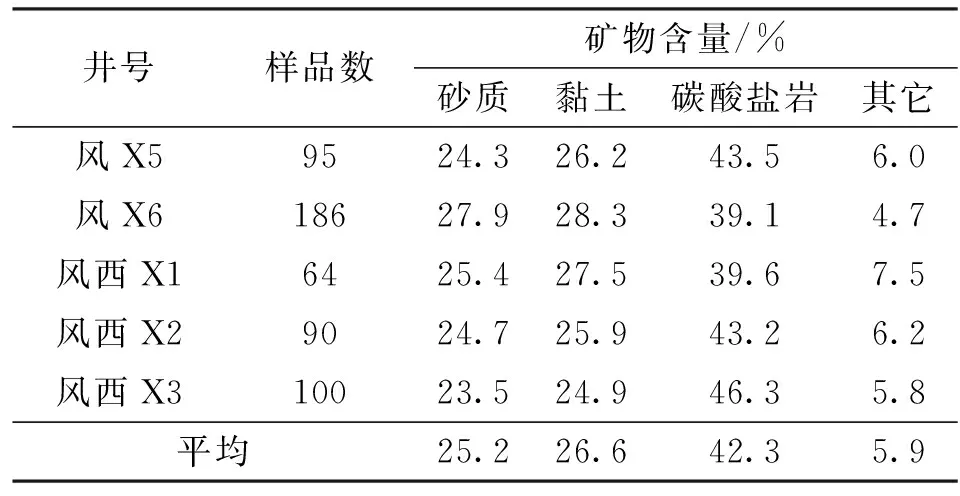
表1 岩心刻度密度模型样本层段X衍射矿物组分统计

由于部分储层碳酸盐含量较高,其骨架组分碳酸盐含量可以达到50%以上,典型藻灰岩层段碳酸盐含量超过65%,导致利用岩心刻度密度模型计算高碳酸盐含量储层孔隙度会偏低,需要对该模型进行修正,以提高高碳酸盐岩储层孔隙度的计算精度。

2.1.3总孔隙度校正模型的确定

由全岩矿物组分测试数据表明,碳酸盐组分中方解石含量在9%～24%、白云石含量在8%～73%,以铁白云石为主。因此,以纯白云石骨架密度2.87 g/cm3作为纯碳酸盐岩骨架密度值。研究区地层水矿化度平均为150 000 mg/L,地层流体密度取1.10 g/cm3,代入密度测井孔隙度理论计算公式,化简得到纯碳酸盐岩孔隙度计算公式

φ0=-56.497ρ+162.15

(7)

式中,φ0为纯碳酸盐岩孔隙度,%;ρ为岩性密度,g/cm3。

对比岩心刻度密度模型趋势线与纯碳酸盐岩理论线,可以看到差别较大(见图2),表明风西湖相复杂混积岩储层的矿物组分复杂,其骨架值与纯碳酸盐岩骨架值有较大区别。从理论上分析,岩石从混积岩过渡到纯碳酸盐岩,其孔隙度—密度关系就会符合碳酸盐含量100%的理论线。岩心刻度密度模型趋势线主要受混积岩矿物组分控制,基本代表了碳酸盐含量在42.3%左右的趋势。两者的不同之处在于斜率和截距的大小。因此,在岩心刻度密度模型趋势线和纯碳酸盐岩理论线之间进行插值,即可确定不同碳酸盐含量情况下的总孔隙度计算模型,并消除用固定模型带来的误差,尤其可以提高碳酸盐含量较高的储层孔隙度计算精度。依据式(6)和式(7),得到风西湖相复杂混积岩储层总孔隙度校正模型

φt=A0×ρ+B0

(8)

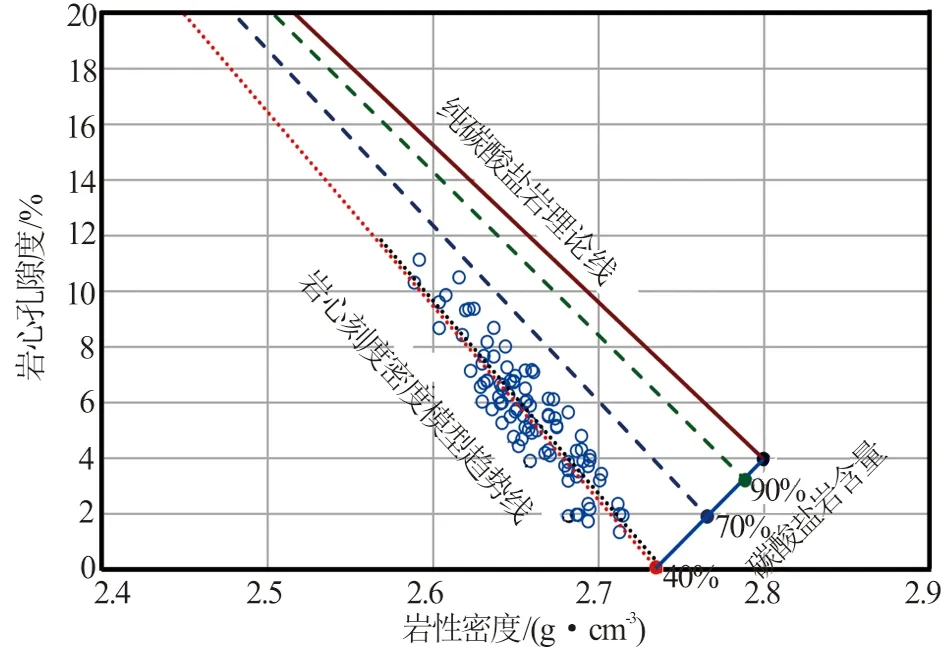
图2 风西湖相复杂混积岩储层(N1—N21)孔隙度校正图版

A0=-78.523+0.2203Vca

(9)

B0=209.79-0.4764Vca

(10)

式中,A0、B0为与碳酸盐含量相关的系数;φt为总孔隙度,%。

利用风西湖相复杂混积岩储层的总孔隙度校正模型对风西X3井X X12.25～X X12.55 m藻灰岩层段进行孔隙度计算。该段X衍射分析得到的碳酸盐含量为73.2%,岩心分析得到的孔隙度为11.3%,岩性密度为2.618 g/cm3,岩心刻度密度模型计算的孔隙度为8.4%;采用总孔隙度校正模型计算的储层孔隙度为11.6%,该值与岩心分析得到的孔隙度误差较小,表明总孔隙度校正模型提高了高碳酸盐含量储层孔隙度的解释精度,提高了模型对岩性频繁变化的适用性。

2.2 有效孔隙度计算模型

由于风西湖相复杂混积岩储层岩性复杂,主要的碳酸盐组分、砂质组分、黏土组分对孔隙有效性的影响不一。为此,以混积岩孔隙的分布和岩性间的相互影响为出发点,提出了孔隙度分配“假想”模型。假设混积岩各组分颗粒是均质的,储层总孔隙度可以表示为3种不同矿物的孔隙度之和,而不同矿物的孔隙度可以按照矿物组分的体积百分比将总孔隙度分配给各种矿物(见图3)。碳酸盐孔隙度模型为式(11),砂质孔隙度模型为式(12),黏土孔隙度模型为式(13)。

φca0=φt×Vca

(11)

φsand0=φt×Vsand

(12)

φsh0=φt×Vsh

(13)

式中,φca0为一次分配后的碳酸盐孔隙度,%;φsand0为一次分配后的砂质孔隙度,%;Vsand为砂质含量,%;φsh0为一次分配后的黏土孔隙度,%。

图3 混积岩储层孔隙度一次分配模型

研究表明,风西复杂混积岩储层孔隙度随着碳酸盐含量的增加而增大、随着黏土含量和砂质含量的增加而减小。因此,设碳酸盐孔隙是有效的,则有效孔隙度表示为

φe0=φca0=φt×Vca

(14)

式中,φe0为一次分配后的有效孔隙度,%。

实际上,储层颗粒存在非均质性,在求取碳酸盐孔隙度时,一次分配后砂质组分和黏土组分中仍可能存在碳酸盐组分,需要多次将砂质孔隙度和黏土孔隙度按照矿物组分的体积百分比进行重新分配,利用多次迭代逼近碳酸盐组分实际的孔隙度(见图4)。二次分配后有效孔隙度模型见式(15),将式(11)～式(13)代入式(15),则式(15)化简为式(16)。

φe=φca0+φsand0×Vca+φsh0×Vca

(15)

φe=φt×Vca×(1+Vsand+Vsh)

(16)

式中,φe为二次分配后的有效孔隙度,%。

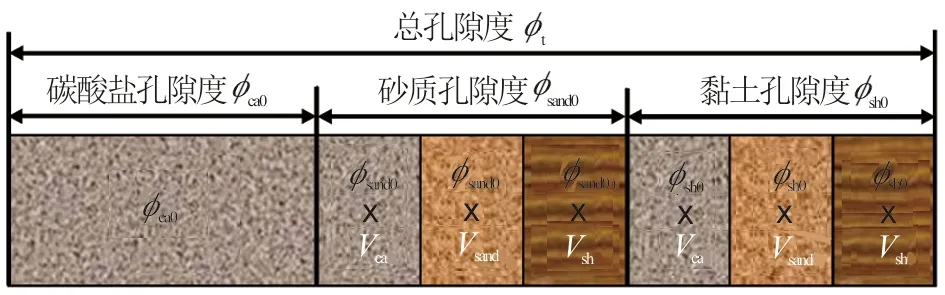
图4 混积岩储层孔隙度二次分配模型

利用核磁共振测井有效孔隙度对不同分配次数的有效孔隙度进行标定。图5为风西X-3井根据常规测井曲线计算的有效孔隙度,可以看出,按各种矿物组分的体积比一次分配得到的有效孔隙度(φe0)与核磁共振测井有效孔隙度具有一定的相关性,但精度较差。按各种矿物组分的体积比二次分配得到的有效孔隙度(φe)与核磁共振测井有效孔隙度相关性好,表明风西地区总孔隙度分配2次后得到的有效孔隙度就可以满足解释的需要。

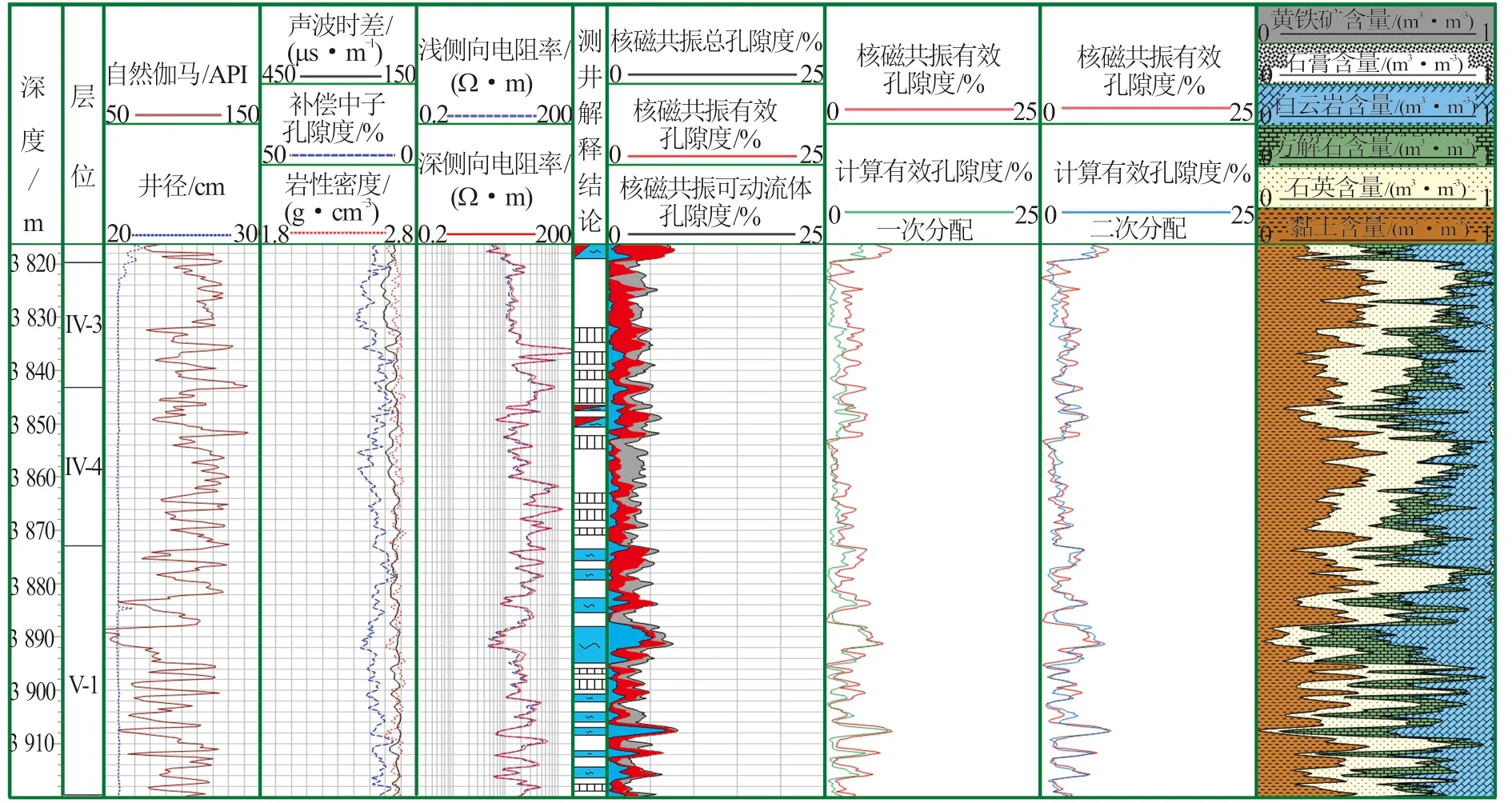
图5 风西X-3井有效孔隙度模型验证

2.3 混积岩储层可动流体孔隙度计算模型

岩心分析表明,风西复杂混积岩储层孔隙度随着黏土含量、砂质含量的增加,孔隙度减小,呈负相关关系。因此,建立束缚水孔隙度与黏土孔隙度、砂质孔隙度的关系就可以求取可动流体孔隙度。根据岩石体积模型(见图6),提出可动流体孔隙度(φf)的基本计算模型

φf=φt-φb

(17)

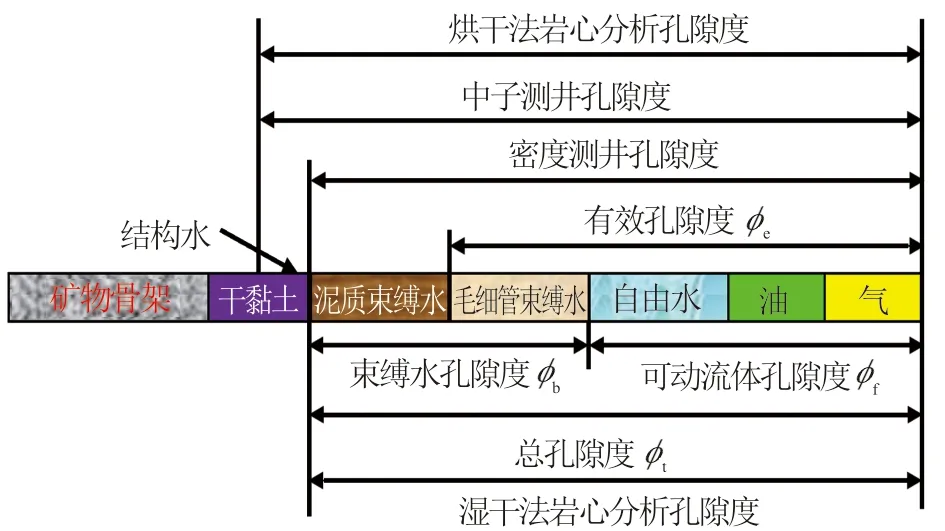
图6 岩石体积模型

式中,φf为可动流体孔隙度,%;φb为束缚水孔隙度,%。

同样,考虑储层颗粒的非均质性,在求取黏土孔隙度或砂质孔隙度时,一次分配后其他2种组分需要进行再次分配。二次分配后,黏土孔隙度的计算模型见式(18),砂质孔隙度的计算模型见式(19)。

φsh=φt×Vsh×(1+Vca+Vsand)

(18)

φsand=φt×Vsand×(1+Vca+Vsh)

(19)

式中,φsh为黏土孔隙度,%;φsand为砂质孔隙度,%。

利用核磁共振测井得到的束缚水孔隙度对黏土孔隙度和砂质孔隙度之和进行标定(见图7),通过对比分析,按照各种矿物的体积比一次分配得到的φsh0和φsand0之和与核磁共振测井束缚水孔隙度具有一定的相关性,但精度较差。二次分配得到的φsh和φsand之和与核磁共振测井束缚水孔隙度相关性好,表明总孔隙度分配2次后得到的φsh和φsand之和可以表征束缚水孔隙度。由式(18)和式(19)可得束缚水孔隙度计算模型为

φb=φt×Vsh×(1+Vca+Vsand)+

φt×Vsand×(1+Vca+Vsh)

(20)

将式(20)代入式(17),则可动流体孔隙度计算模型为

φf=φt-φt×Vsh×(1+Vca+Vsand)-

φt×Vsand×(1+Vca+Vsh)

(21)

图7 风西X-3井束缚水孔隙度模型验证

3 结论与建议

(1)通过敏感曲线分析,应用归一化处理的相对曲线建立了矿物组分解释模型,提高了矿物组分计算的精度。

(2)岩心刻度与理论模型结合,建立的混积岩储层孔隙度校正模型,大幅度提高了混积岩储层总孔隙度计算精度,提高了模型对岩性频繁变化的适用性。

(3)以混积岩储层孔隙的分布和矿物组分间的相互影响为出发点,提出了孔隙度分配“假想”模型,尽管岩石的有效孔隙度和可动流体孔隙度的计算方法可能和实际情况存在一定差距,但最终利用岩心分析数据和核磁共振测井结果进行标定验证,建立的计算方法满足风西复杂混积岩储层有效孔隙度和可动流体孔隙度解释的需要。

(4)本文采用的技术对柴达木盆地柴西北复杂混积岩储层的测井评价具有推广和借鉴意义,可以降低特殊测井成本。