中低速动车组弹性复合圆柱滚子轴承承载能力分析*

杨 文,姚齐水,余江鸿,童忠文,黄剑锋*

(1.湖南铁道职业技术学院 轨道交通装备智能制造学院,湖南 株洲 412001;2.湖南工业大学 机械工程学院,湖南 株洲 412007)

0 引 言

提高列车的运行速度,以及在普通铁轨(俗称既有线)上运行中低速动车组,是我国经济发展的战略需要。动车组在服役过程中,由于受到来自普通轨道不平顺作用下复杂载荷的作用,其运行的安全性和可靠性成为了相关部门关注的焦点[1]。

转向架轮对是机车行走部集成式功能部件,由车轮、车轴及轴箱轴承等构成[2]。在其服役过程中,列车车重载荷自上而下通过轴箱轴承、车轴以及车轮传递到铁轨,各部件均承受着普通轨道不平顺作用下的复杂载荷。

轴箱轴承失效是动车组轮对主要失效形式之一。在普通轨道的不平顺作用下,动车组轮对轴箱轴承承受车辆随机振动载荷、弯扭载荷及冲击载荷,使其内部各组件会产生剧烈的相互作用,从而造成较大的接触疲劳,再加上其长期复杂且恶劣的工作环境,会最终导致轴箱轴承的疲劳损坏。这是轴箱轴承的主要失效形式之一[3,4]。

为了提高轴箱轴承的承载能力,国内外学者都已经做了大量的研究工作。LUNDBERG G[5]对母线进行了修形理论分析,提出了Lundberg凸度公式。SINGH K P[6,7]和HARMETT M J[8]提出了一种简单的离散化数值解法,并构造了线性方程组,对带凸度圆柱体进行了接触应力计算。

上述的母线修型和凸度计算方法有效地降低了轴承因“边缘效应”而导致的疲劳破坏程度,然而并没有能够有效地改善轴承的承载能力。

在针对滚动轴承疲劳寿命数值仿真技术的研究中,吕华强等人[9]提出了一种滚动轴承疲劳寿命预测系统。杨继运等人[10]通过分析损伤力学理论,建立了一种基于损伤力学—有限元法的理论体系。张雪等人[11]采用有限元法对交叉滚子转盘轴承的接触应力和次表面应力进行了分析。

以上学者针对轴承疲劳寿命进行了预测系统、损伤机理等方面的研究,然而也没有从根本上改善轴承的承载能力。

黄运生[12]对轨道不平顺下轴箱轴承受到冲击载荷进行了分析,对轴箱轴承的剩余寿命进行了评估。在轴箱轴承方面,很多学者的研究主要集中在对轴箱轴承疲劳寿命进行分析,以及轨道不平顺对轴箱轴承疲劳寿命的影响上。研究的出发点是为了给轴箱轴承的选型和应用提供较好的方案,然而这并未改变轴箱轴承易摩损的特征。轨道不平顺作用下轴箱轴承各组件间发生疲劳破坏的原因主要是接触碰撞和磨损,因此,上述研究也没有从结构上改善轴箱轴承的承载能力。

弹性复合圆柱滚子轴承是一种新型的滚动轴承[13,14]。有研究人员通过对弹性复合圆柱滚子轴承进行结构创新,即在空心圆柱滚子内嵌高分子材料PTFE,形成了刚柔耦合的滚子,增大了滚子与其他组件的接触面积,降低了低组件间的接触应力,有效提升了圆柱滚子轴承的承载性能[15]。

因此,笔者构建基于新型轴承的动车组轮对力学模型,在轨道不平顺引起的复杂载荷下,通过有限元方法确定应用于动车组轮对的弹性复合圆柱滚子轴承滚子最优结构,对比分析相同工况下弹性复合圆柱滚子轴承和普通圆柱滚子轴承的承载能力各项指标,从而提升轮对结构的承载能力,提高其安全性和可靠性,为拓宽动车组轮对支承系统设计提供思路。

1 动车组轮对力学模型

轮对是动车组行走部核心部件,其在运行过程中承受复杂且随机的载荷。在轨道不平顺作用下,动车组轮对疲劳失效主要考虑超常载荷和常规载荷。其中,超常载荷是动车组轮对在轨道不平顺等因素作用下产生的较大冲击载荷,它可作为动车组轮对的静态设计依据。动车组轮对在运行中基本上是承受交变载荷,较为频繁的交变载荷对整个动车组轮对的使用寿命有着重要影响,它为动车组轮对疲劳分析和试验提供了准静态和动态载荷值。

在轨道不平顺等因素作用下,笔者主要考虑弹性复合圆柱滚子轴承对动车组轮对结构超常载荷的影响。动车组转向架承受车辆载荷并传递到轮对,承受整车车体及转向架的载荷,包括作用于轴箱轴承座的垂向载荷、横向载荷和纵向载荷。

依据载荷分布,笔者构建了动车组转向架力学模型[16],如图1所示。

图1 动车组转向架主要载荷示意图

(1)垂向载荷

垂向载荷的表达式为:

(1)

式中:Fz—构架超常垂向静载荷,N;G—车辆的重量,N;G1—旅客和行李的重量,N;G2—转向架的重量,N;nb—转向架数;k—动荷系数,一般取1.4。

轮对轴颈载荷为:

Q1V=Q2V=Fzmax/4

(2)

(2)横向载荷

横向载荷的表达式为:

(3)

式中:nb—转向架数;ne—轮对数。

如果二系悬挂的横向刚度为L,横向止挡间隙为M,则二系悬挂所分得的载荷为:

Fy1=Fy2=LM

(4)

一个横向止挡所分得的载荷为:

Q1H=Q2H=Fymax-(Fy1+Fy2)

(5)

(3)纵向载荷

在转向架构架上施加一个纵向牵引载荷,该载荷为:

Fx=kxgmb

(6)

其中:kx一般取3。

笔者结合转向架静力学分析,对动车组轮对的力学模型进行重构,确定动车组轮对在服役中承载的力学模型,如图2所示。

图2 动车组轮对力学模型

动车组轮对通过两侧轴箱体以及悬挂系统与转向架连接,承受整车车体及转向架的载荷,将轨道不平顺作用下形成的冲击载荷通过叠加,有效反馈到轴箱体上,包括作用于轴箱体的垂向力P1V、P2V,横向力P1H、P2H和纵向力P1L、P2L;铁轨承载源于轮对的整车车体及转向架的载荷,作用于左右车轮的垂向力Q1V、Q1H,横向力Q1L及Q2V和纵向力Q2H和Q2L。

2 有限元模型及分析

基于动车组轮对受到的复杂载荷作用,并考虑到动车组轮对各部件之间相互作用,以及弹性复合圆柱滚子轴承刚柔耦合结构的特性,无法通过Hertz接触理论对复杂的轮轨接触问题和刚柔耦合问题进行理论分析计算,而采取数值分析法是解决该问题更有效的方法。因此,笔者利用ABAQUS仿真软件对动车组轮对进行有限元建模和数值分析。

2.1 几何模型和材料特性

针对轮对的分析,主要是考虑车轮—车轴、车轴—轴承、车轮—轨道之间的联系和相互影响。由于车轮、车轴、轴承以及轨道的受力是相互的,而且比较复杂,需要对轮对系统进行整体分析。

笔者建立了包含2个机车车轮、1根车轴、轴箱(包括轴承和轴箱体)及部分轨道的轮对有限元模型,如图3所示。

图3 轮对三维模型

为了保证有限元分析的准确性,同时兼顾计算的效率,笔者在建模时简化了结构[17],并忽略了轮对系统不影响接触分析的微小几何特征。

轮对各个部件名称以及材料性能参数如表1所示。

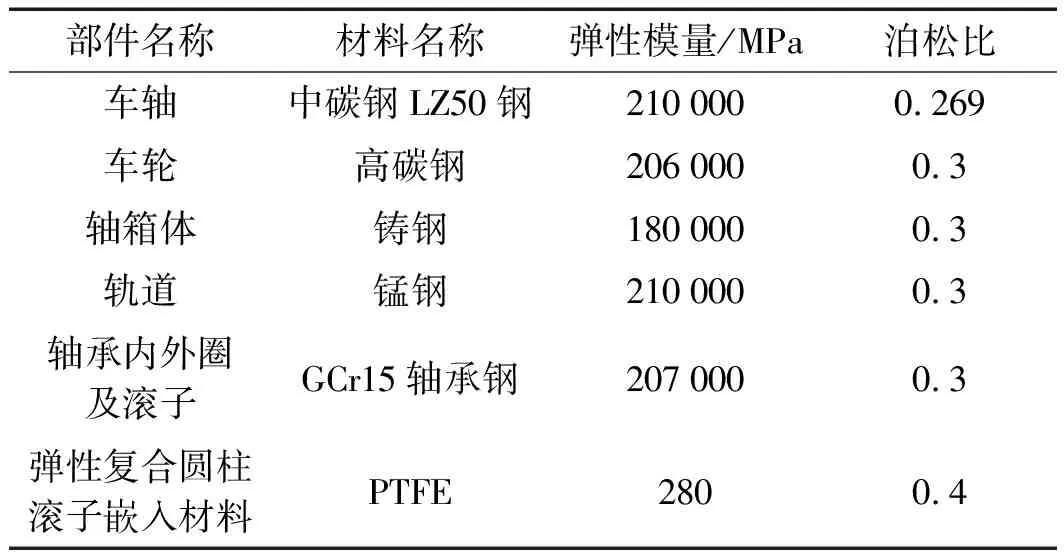
表1 轮对各部件材料属性

2.2 边界和载荷定义

根据整体模型的特点,笔者对轨道底部建立全约束,车轴端面约束U2、UR1和UR3 3个方向的自由度,车轮侧面约束U1、U2和UR3 3个方向的自由度,轴承侧面约束U2方向的自由度,轴箱体侧面约束U1、UR1、UR2和UR3 4个方向的自由度。

笔者对动车组轮对的载荷约束采取静态分析力学模型进行重构,主要包括垂直载荷、横向载荷和纵向载荷,即设作用于轴箱体的垂向力P1V、P2V,横向力P1H、P2H和纵向力P1L、P2L,并将上述作用力加载于轴箱体上。

2.3 接触建立和网格划分

在模型中,车轮与轨道、车轮与车轴、车轴与轴承内圈、轴承外圈与轴箱体以及弹性复合圆柱滚子中两种材料之间都形成紧密配合,通过车轮接触面、车轴接触面、轴承内圈接触面、轴承外圈接触面和滚子内圈分别与轨道接触面、车轮接触面、车轴接触面、轴箱体接触面和填充材料外圈之间建立接触对。

网格的精确性直接关系到数值计算的效率以及计算结果的准确性。笔者通过数值计算,并考虑分析对象的几何形状、载荷条件、材料组合等因素,进行了网格划分。合理的模型网格划分结果为:动车组轮对的实体单元数1 168 944个,节点数1 489 635个。

2.4 计算方案

根据上述有限元网格划分结果可知,结构大而杂的轮对结构需要超大的计算量,且其对于较小的轴承结构不能进行精准计算。为此,笔者通过将轮对有限元计算过程分“整体”、“局部”两个部分分别进行,以避免超大计算和计算不精准问题,具体的做法如下:

(1)整体计算。先设置弹性复合圆柱滚子轴承和轴箱体之间的关系固定不变,内部建立集成消除滚动接触接触副,滚子-滚道实体建立连接,模拟刚度接近的“等效轴承”;采用修正的二次四面体单元(C3D10M)划分网格。这样,车轮-车轴-虚拟轴承-轴箱-轨道构成了轮对有限元整体计算模型,共有1 168 944个单元、1 489 635个节点;

(2)局部计算。以整体计算模拟圆柱滚子轴承和轴箱体的产生的当量载荷作为约束,轴承的滚子-内外圈恢复接触关系,形成局部计算模型,其网格单元数271 962个,节点数325 729个。

3 直道工况算例

此处以直道运行工况为例,笔者根据AARS660标准以及EN13979-1标准,由上述平衡力系计算获得动车组轮对直道运行的常规载荷,并考虑轨道不平顺作用下产生的超常载荷,获得了动车组直道运行工况下总体载荷。

具体载荷值如表2所示。

表2 动车组直道运行工况载荷

笔者采用有限元方法先进行整体计算,再以当量载荷作为约束,对轴承进行局部计算。

首先,笔者在考虑常规载荷和超常载荷工况下,对应用于动车组轮对的弹性复合圆柱滚子轴承的填充度进行优选;再以弹性复合圆柱滚子轴承和普通圆柱滚子轴承作为动车组轮对关键支撑零部件,对其承载能力进行对比计算。

3.1 弹性复合圆柱滚子轴承填充度优选

弹性复合圆柱滚子轴承滚子由深穴空心圆柱滚子内嵌高分子材料PTFE形成,其结构示意图如图4所示。

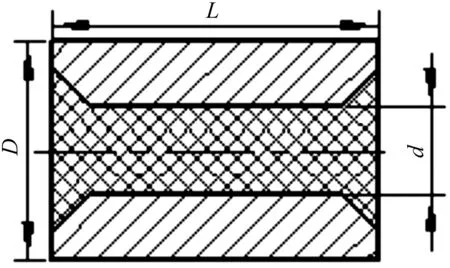
图4 弹性复合圆柱滚子结构示意图

笔者定义弹性复合圆柱滚子的填充度为:

K=d/D

(7)

式中:K—填充度;d—弹性复合圆柱滚子内孔直径,mm;D—弹性复合圆柱滚子直径,mm。

接触应力、等效应力是轴承承载能力的重要指标,笔者结合动车组轮对直道运行的实际工况,并考虑了常规载荷和超常载荷,对不同填充度的弹性复合圆柱滚子轴承进行了数值分析计算。填充度过小,则无法体现弹性复合圆柱滚子性能优势;填充度过大,则轴承的承载能力过低。

因此,此处笔者选择填充度为40%～70%(跨度为5%)的弹性复合圆柱滚子轴承进行分析和优选。不同填充度情况下,弹性复合圆柱滚子与内外圈接触的最大接触应力和最大等效应力,如图5所示。

由图5(a)可知,常规和超常两种载荷下,填充度60%的弹性复合圆柱滚子的最大接触应力最小;据图5(b)可知,常规载荷下的弹性复合圆柱滚子轴承填充度为65%时,其最大等效应力最小,而超常载荷下填充度为60%时,其最大等效应力最小。

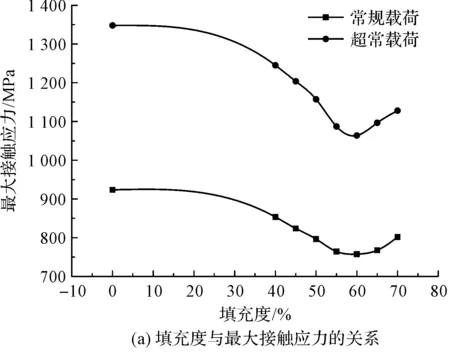
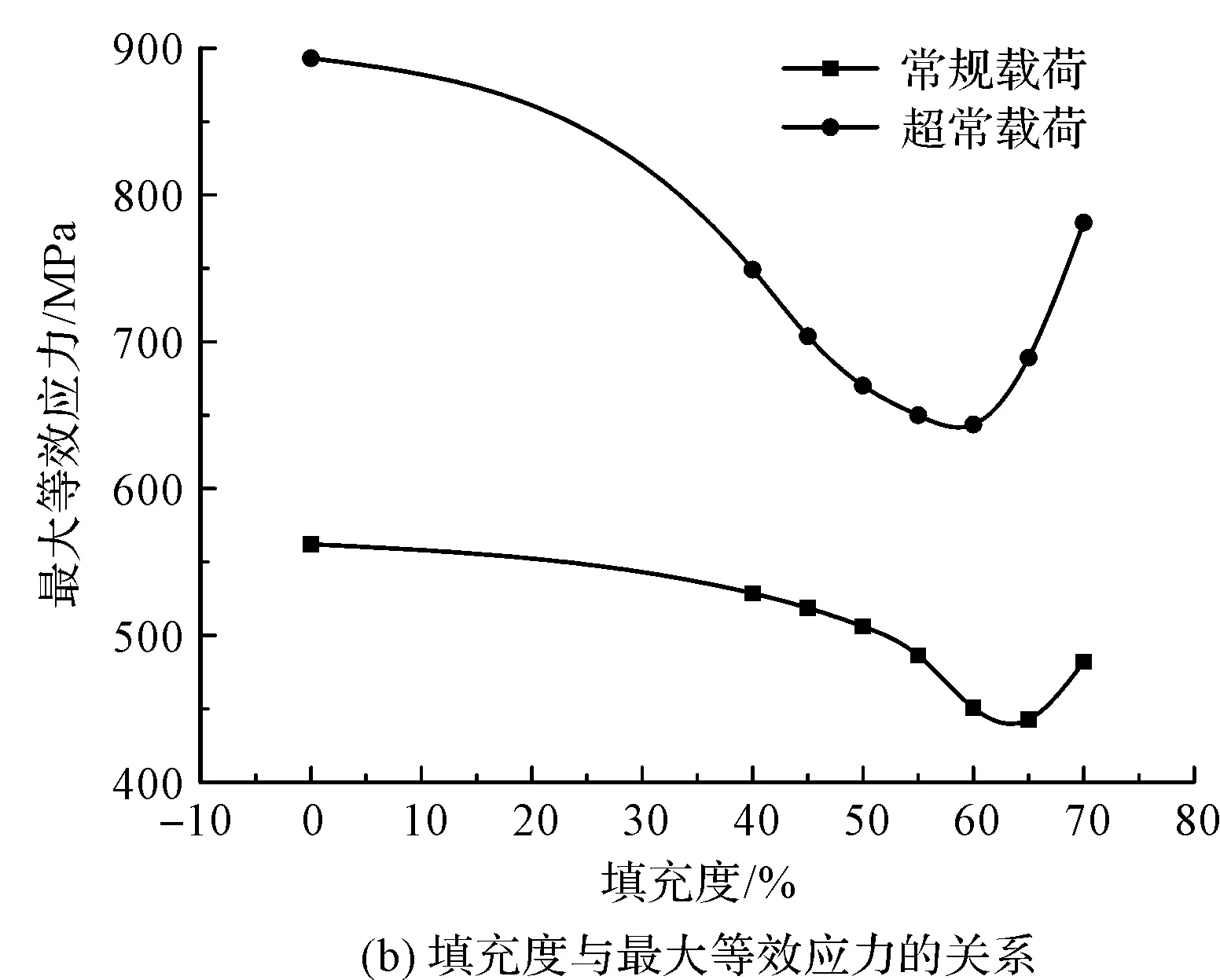
图5 填充度与最大应力的关系

由于等效应力是轴承疲劳寿命的关键因素,笔者经综合考虑确定最优填充度K为60%。

3.2 两种轴承对比

在常规载荷和超常载荷下,普通圆柱滚子轴承和弹性复合圆柱滚子轴承的有限元对比计算结果如表3所示。

表3 有限元计算两种轴承的等效应力结果

由表3可知:

(1)在相同载荷下,两种轴承处在载荷复杂的轮对结构中所受的应力不同;

(2)在常规载荷下,普通圆柱滚子轴承的最大应力值为562.1 MPa,位于最下端滚子与内圈接触的次表面,而弹性复合圆柱滚子轴承最大应力值为450.7 MPa,所处位置也在最下端滚子与内圈接触的次表面,后者较前者接触应力要小21.2%;

(3)在超常载荷下,弹性复合圆柱滚子轴承的最大等效应力较普通圆柱滚子轴承降低了27.92%,其最大等效应力位置也处在滚子与内圈接触的次表面,表明了弹性复合圆柱滚子轴承应用于动车组轮对的承载能力较普通圆柱滚子轴承更具有优势。

4 接触应力试验

接下来笔者通过轴承试验台对接触应力进行试验研究。此处笔者选择ZNXGZ-50B新型滚动轴承综合试验台。该轴承综合试验台采用模块化设计,实现了数据采集、工况控制以及结果输出的自动化,具有测试精度高等的特点。

ZNXGZ-50B新型滚动轴承综合试验台实物图如图6所示。

图6 ZNXGZ-50B型滚动轴承综合试验台

4.1 方案

在相同载荷试验条件下,笔者通过测试试验,对比分析应用于动车组轮对的两种轴承的等效应力。

笔者将试验轴承安装在轴承试验台上,通过加载系统模拟动车组轮对的受力,给试验轴承施加垂向、横向和纵向3个方向的载荷。

被施加载荷后的轴承滚子会出现接触变形,轴承内外圈也会发生变形,轴承内外圈各个测试点也会将对应的应变大小通过动静态电阻应变仪显示出来,从而得出试验轴承滚子的接触应力大小。

4.2 结果与分析

笔者通过加载系统和压力传感器,对试验台进行径向加载(垂向载荷与纵向载荷合成为径向载荷)和横向加载。其中,径向加载依次增大分别为0 kN、20.5 kN、41 kN、61.5 kN、82 kN,结合动车组轮对直道运行常规载荷的工况,横向加载为0。

笔者通过动静态应变测试仪记录了3个通道的试验数据,得到了普通圆柱滚子轴承和弹性复合圆柱滚子轴承的最大接触应力情况,如表4所示。

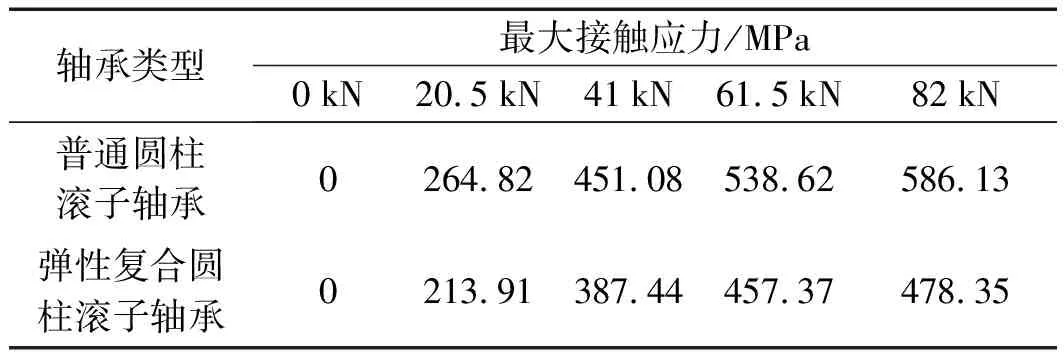
表4 不同载荷下两种轴承的最大接触应力(MPa)

根据表4可知,随着载荷的不断增大,两种轴承接触应力均增大,且呈现非线性增大。当试验载荷增加到与仿真载荷82 kN相等时,两种轴承的最大接触应力分别为478.35 MPa和586.13 MPa。

两种轴承的试验结果与仿真结果对比如表5所示。

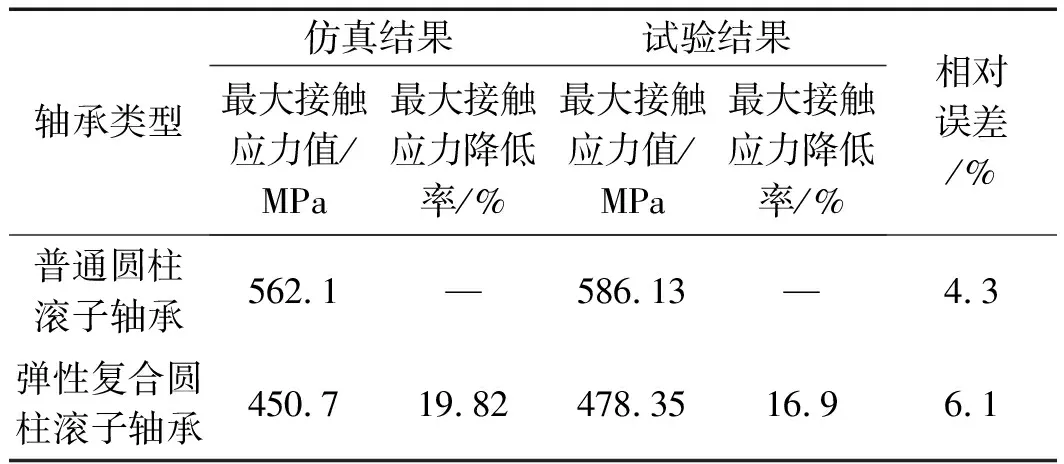
表5 两种轴承的试验结果与仿真结果对比

从表5对比可知:试验结果与仿真结果基本吻合,存在误差在10%以内。这主要是因为仿真模型是在对实物作了部分假设的基础上建立的,而且试验设备自身存在的误差,总体上该误差在工程分析允许的范围内。

综上所述,笔者建立上述仿真模型,用于分析动车组轮对轴承,具有较高的准确性,也体现了弹性复合圆柱滚子轴承应用于动车组轮对的优越性。

5 结束语

为了有效改善动车组轴承的承载能力,笔者提出了一种弹性复合圆柱滚子轴承应用于动车组轮对,并对其支承性能进行了研究,最后通过试验进行了验证。

研究结果表明:

(1)通过结合动车组轮对的常规载荷和超常载荷实际工况对弹性复合圆柱滚子轴承进行有限元计算,确定其最优填充度为60%;

(2)在常规载荷和超常载荷下,通过基于弹性复合圆柱滚子轴承和普通圆柱滚子轴承的动车组轮对有限元对比计算,结果表明,两种载荷下前者较后者最大等效应力分别下降了19.82%和27.92%,试验结果与仿真结果基本吻合。

综上所述,弹性复合圆柱滚子轴承应用于动车组轮对具有良好的承载能力。笔者在后续的工作中,将对动车组弹性复合圆柱滚子轴承动力学特性及其振动机理进行研究。