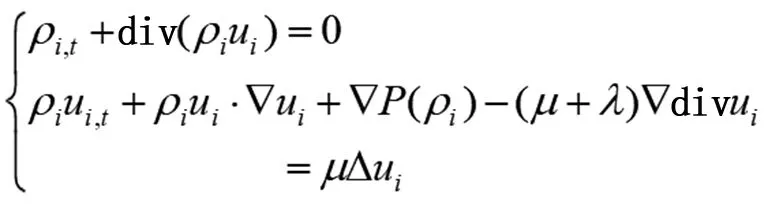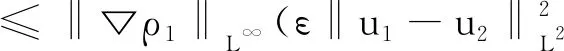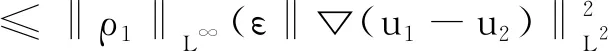三维可压缩 Navier-Stokes 方程解的连续性

王朋杰, 张 洁

( 贵州师范大学 数学科学学院，贵州 贵阳 550025 )

我们考虑如下方程

(1)

其中t≥0,x∈Ω,Ω为R3中一个带有紧支撑集和有光滑边界的区域。其边界条件为

u|∂Ω=0

式中u=(u1,u2,u3),ρ分别是流体运动的速度和密度，p(ρ)是压强，μ和λ是黏性系数，并且满足2μ+3λ≥0。 任何物质的运动都受到一定的自然规律(如物理定律)的制约。 常见的一些数学物理方程作为描写物质运动的数学模型，是从数量形式上刻画了由相应的物理定律所确立的某些物理量之间的关系[1]。质量守恒、动量守恒和能量守恒是自然界一切遵循的定律，根据守恒律,能够列出符合问题的微分方程。利用能量法, 人们已经知道经典的三大方程解具有稳定性。对于三维可压缩 Navier-Stokes方程，用类比的方法同样能得出其解的稳定性。

1 预备知识

引理1[2]Gronwall不等式的微分形式。设η(t)是[0,T]上的非负、绝对连续函数，且几乎处处满足微分不等式

η′(t)≤φ(t)η(t)+ψ(t)

其中，φ(t)和ψ(t)在[0,T]上非负可积，则有

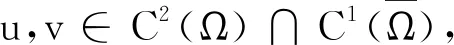
其中n是∂Ω上的单位外法向。

引理3[2]Poincare不等式。设Ω是Rn中的有界连通开集且在边界取值为0，1≤p≤∞，则成立不等式

‖u‖Lp(Ω)≤C‖Du‖Lp(Ω)

其中C与n,p,Ω有关。

2 主要结论

定理对于三维可压缩Navier-Stokes方程组(1)在其初值条件(ρ,u)|t=0=(ρ0,u0)，边值条件u|∂Ω=0条件下，此问题的解在平方模的意义下对初始值具有连续依赖性，即初始数据变化很小时，对应的解变化也很小。

证明假设(ρ0,1,u0,1)和(ρ0,2,u0,2)为问题 (1)的两个光滑初始值，且0

(2)

其中i=1,2。当i=1和i=2时，两式分别作差得到

(ρ1-ρ2)t+div[ρ1(u1-u2)+u2(ρ1-ρ2)]=0

两端同时乘以(ρ1-ρ2) , 并在Ω上积分可得

对上式右端变形得到

+divu2(ρ1-ρ2)+u2▽(ρ1-ρ2)]dx

对于I1有

(3)

同理对于I2有

(4)

对于I3有

(5)

对于I4有

(6)

综上有

(7)

同理对于(2)中的第二个式子我们有

ρ1(u1-u2)t+u2,t(ρ1-ρ2)

+(ρ1-ρ2)u2▽u2+ρ1[(u1-u2)▽u2

+u1▽(u1-u2)]+▽(ρ1γ-ρ2γ)

-(μ+λ)▽div(u1-u2)

=μΔ(u1-u2)

(8)

在上式两端同时乘以(u1-u2), 并在Ω积分可得

(9)

对(9)左端逐项估计， 注意到

ρ1(u1-u2)t(u1-u2)

对K1的估计有

(10)

对 (10)的第二项估计有

(11)

对K2有

|K2|≤‖u2,t‖L∞‖ρ1-ρ2‖L2‖u1-u2‖L2

(12)

同理对K3,K5,K6有

(13)

(14)

(15)

对于K4来说

(16)

(17)

同理对于 (9)右端

(18)

取ε适当小

(19)

考虑到(7)和 (19), 两式相加可得

(20)

注意到m≤ρ1≤M，进一步有

(21)

对 (21)应用Gronwall 不等式得

(22)

由 (22) 知道三维可压缩 Navier-Stokes 方程初边值问题的解对初值的依赖性， 即当初始数据变化很小时,对应的解也只是有相应的微小变化,说明这个问题的解是稳定的。