基于集中式变流器的风电机群功率输出控制
2022-04-22熊国专杨培文张金强张悦超
熊国专 胡 鹏 杨培文 张金强 张悦超
(龙源(北京)风电工程技术有限公司)
0 引言
近海风电具有风速高、湍流强度小、风速风向稳定等优点,且我国海岸线长,具备大规模发展海上风电的资源条件,同时沿海地区矿产资源匮乏,电力需求巨大,海上风电可以就近吸纳,因此近海风电的发展具有巨大的潜力[1-2]。受极端天气和海洋环境的制约,海上机组维护成本高、维护难度大,长时间故障停机导致的发电量损失巨大[3-4]。对此,有国内外研究学者提出风电机群集中控制的思想,即利用单台变流器控制多台风机取代单台变流器控制单台风力机,这将有利于减少单台变流器独立控制带来的建设和维护成本[5-7]。其中部分研究提出采用结构坚固可靠的鼠笼式异步发电机取代其他机组,来进一步提高风电系统的可靠性,延长机组有效发电时长[6-7]。对于风电机群集中控制而言,连接至同一条变频交流母线上的所有风力机转速相同,即运行于风电机群同一转速。当各台风力机处的风速大小不一时,则会存在风力机偏离于最佳的叶尖速比,从而导致一定的风速损失。AgustíEgea-Àlvarez等人通过磁链观测器计算出风电机群的转速平均值,进而得到含有转速平均值变量的转矩公式,并通过风电场功率控制器使系统转矩给定值最优来获得最佳的风能捕获状态[6],但其未考虑到如何控制风速较高的风电机组输出功率不超过额定值。Si-Zhe Chen提出利用粒子群搜索算法对风电机群同一转速和全体风力机桨距角进行协同优化,来进一步提高风能利用率,同时实现恒功率控制[7]。粒子群算法作为一种模糊搜索算法,当风电机群规模扩大时,待求解变量增多,其收敛速度快的优势将不明显,且易陷入局部最优解。基于以上不足,本文采用了一种简易的功率输出控制算法,能够根据风速变化实时快速求解最优解。在低风速时,将风机的桨距角置零,简化风能利用系数公式,从而求解最优的风电机群同一转速,来获得较高的风能利用率,对于风速过高的风力机可利用桨距角的调节作用来达到恒功率输出的目的。
1 集中变流控制拓扑结构
图1为基于高压直流输电的分布式变流发电与集中式变流发电拓扑结构图。
传统的海上分布式变流发电技术为每台机组提供局部变流器,经变频交流母线汇流后连接至风电场侧变流器转为高压直流,用于长距离传输至岸上。国外学者提出了一种基于多端口的高压直流输电近海风电机群集中控制拓扑[5],如图1下部分,每条变频交流母线上连接一组风力发电机,通过各自的集中式变流器转为直流电后汇聚一起,再进行高电压传输。集中式变流器大大减少了为每台机组配备变流器的昂贵支出,且省去了中间变流环节导致的电力消耗。然而对于集中式变流发电而言,同一条变频交流母线上的所有风力机均运行于同一转速,受尾流效应影响各台风力机处的风速大小不一致时,存在风力机偏离于自身的最佳叶尖速比,这将会导致一定的风能损失。这种损失是不可避免的,只能通过寻找最优的风能捕获算法去尽可能减少。

图1 分布式变流与集中式变流拓扑结构图
2 变最大功率输出控制算法
根据贝茨理论,风力机的机械输出功率输出公式:

式中,Pt为风力机输出的机械功率;A为叶片扫掠面积;ρ为空气密度;V为风速;Cp为风能利用率,是叶尖速比和桨距角的函数:

式(2)中,β为桨距角;λ为叶尖速比,可表示为:

式(3)中,ωt为风力机转速;R为叶片长度。
根据式(2)绘制不同桨距角下的风能利用系数曲线,如图2所示。
由图2可见,不同的桨距角β所对应的最大风能利用系数不同,当桨距角β=0o时的风能利用系数最大,为0.48。
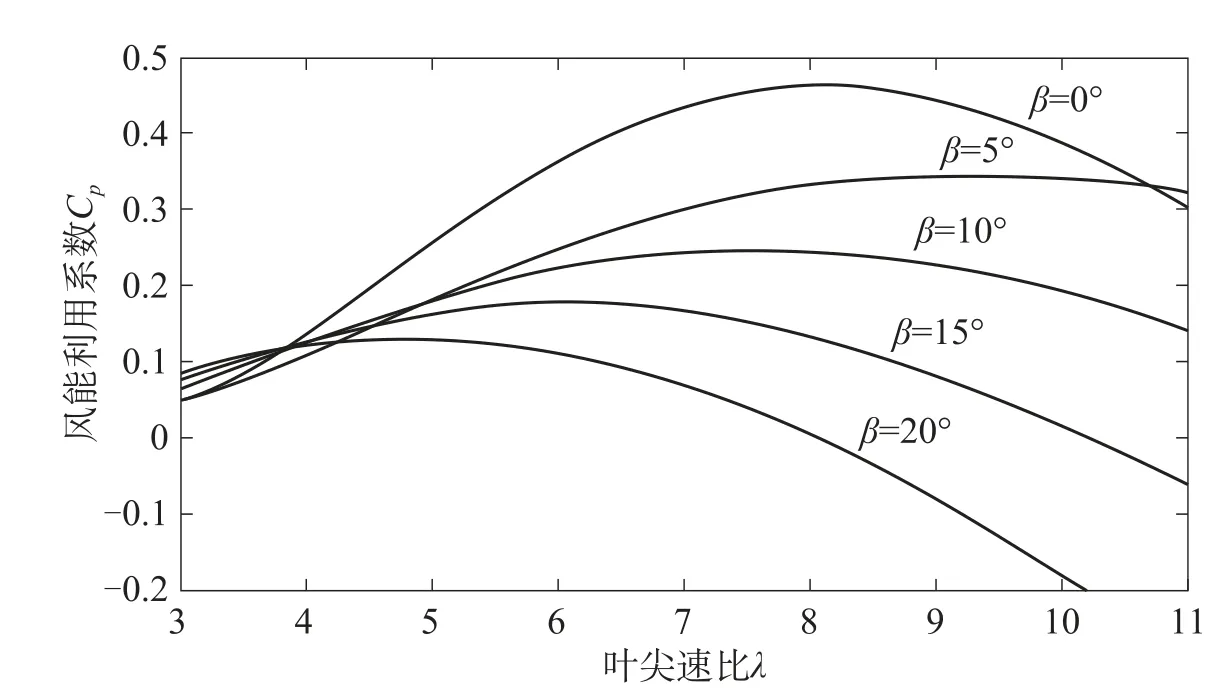
图2 不同桨距角下的风能利用系数曲线
考虑到桨距角β=0时,风力机的风能利用系数Cp最大,故可将式(2)中的桨距角β置0,同时通过曲线拟合算法将式(2)简化为如式(4)所示的五次幂多项式:
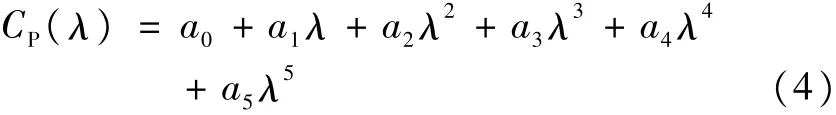
其中,a0~a5依次为0.68557493、-0.65617388、0.21623231、-0.02688719、0.00145086、-0.00002965。
M台并联运行的风电机组总输出功率如下:
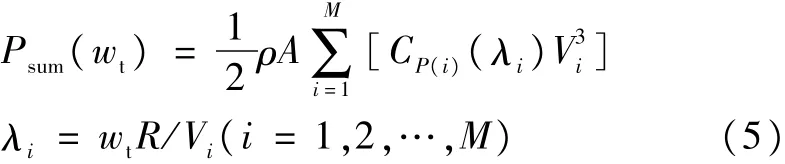
由式(5)可知,当各台风力机处风速已知的情况下,风电机组总输出功率仅与风电机群同一转速ωt有关,对M台风电机组总输出功率求导,求导公式如下:

对式(6)中的四次五项式求根,即可得出最佳的风力机群同一转速ωopt。当风速过高时,存在发电机输出功率将超过额定值,此刻可控制发电机运行于额定转速ωn,由式(1)~式(3)可知,若要使发电机运行于额定功率输出,可通过桨距角的调节作用来实现。
3 笼型异步发电机群直接转矩控制策略
笼型异步发电机在两相静止坐标系α、β下的数学模型如下[8]:
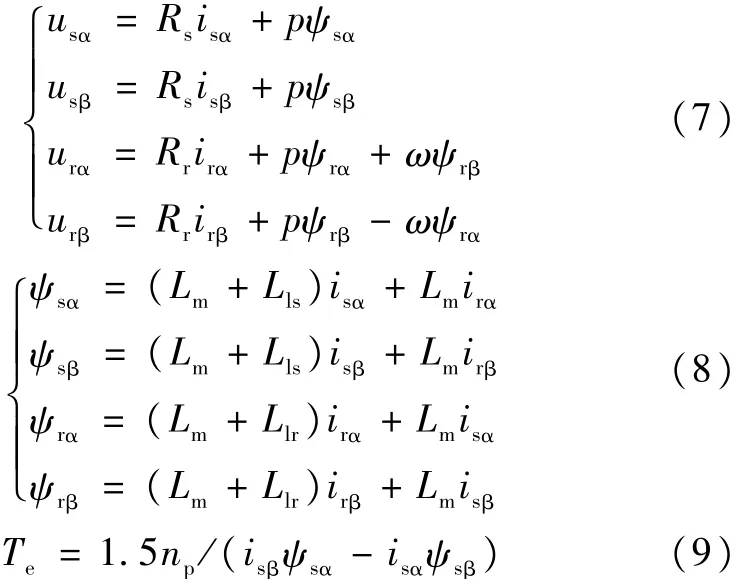
其中,usα、usβ、urα、urβ表示发电机定、转子电压在α、β轴上的分量;isα、isβ、irα、irβ表示发电机定、转子电流在α、β轴上的分量;ψsα、ψsβ、ψrα、ψrβ表示发电机定、转子磁链在α、β轴上的分量;Te表示发电机的电磁转矩;np表示发电机的极对数。
笼型异步发电机与风力机之间的运动方程式如下:
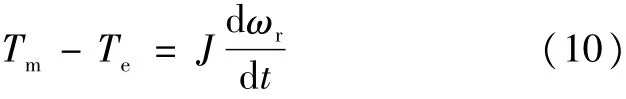
笼型异步发电机群直接转矩控制策略框图如图3所示,采集各台风力机的实时风速输入功率输出算法模块,产生对应于最大功率输出的风电机群同一给定转速和各风力机桨距角的给定值。将风电机群同一转速给定值与反馈值的偏差输入PI调节器,产生转矩电流给定值;转矩电流给定值与反馈值的偏差经PI调节器产生q轴输出电压;磁链给定值与反馈值的偏差经PI调节器产生励磁电流给定值,励磁电流给定值与反馈值的偏差经PI调节器产生d轴输出电压;dq轴电压经旋转/静止变换和SVPWM调制后,产生风电场变流器的驱动脉冲。
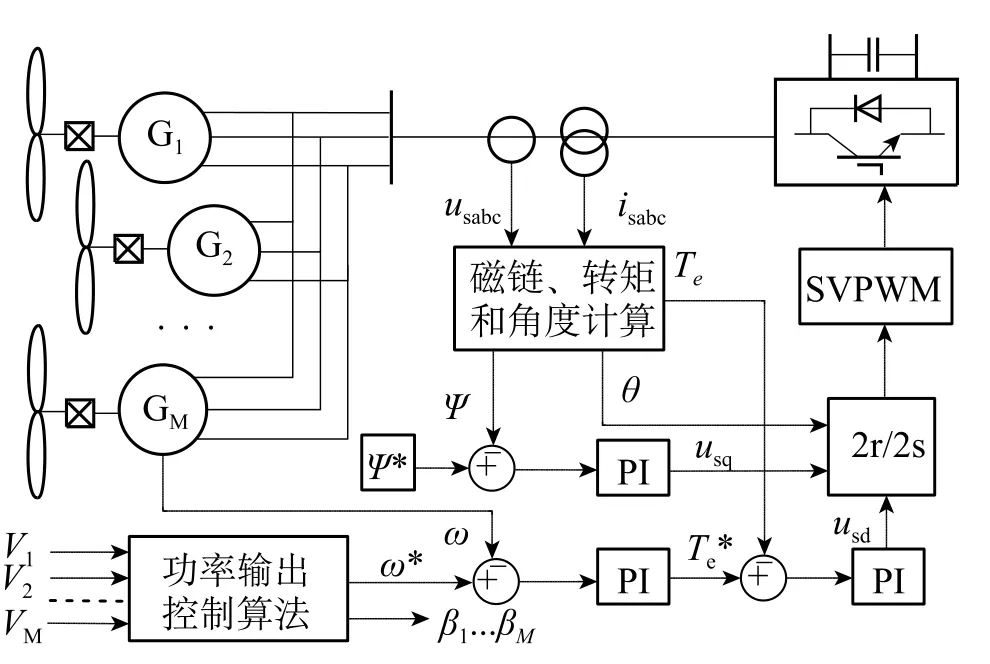
图3 笼型异步发电机群直接转矩控制策略框图
其中,磁链和角度计算公式如下:

其中,Rs为发电机定子绕组阻值。
4 笼型异步发电机群直接转矩控制策略
为验证本文所提出的功率输出控制算法的有效性,在Matlab/Simulink仿真平台搭建如图3所示的笼型异步发电机群,为加快系统的仿真速度,选取了4台额定功率为149.2kW的笼型异步发电机进行仿真分析。其中,标幺值系统中的基准值为:风速vbase=12m/s,最佳叶尖速比λopt=8.1,风能利用系数Cp_max=0.48,额定转速ωn=1800r/min。其余系统仿真参数如下表所示。

表 笼型异步发电机参数
考虑到风电场各台风力机处风速之间的差异,给出了由基本风速、斜坡风速、阵风和湍流叠加组成的四组低风速,如图4所示,实时计算的仿真结果如图5、图6所示。
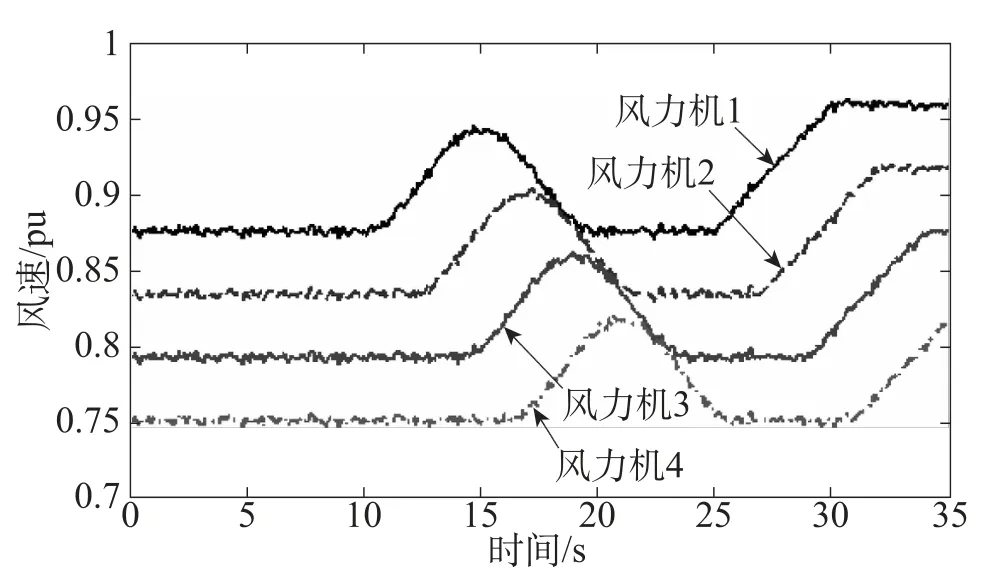
图4 各台风力机处的风速
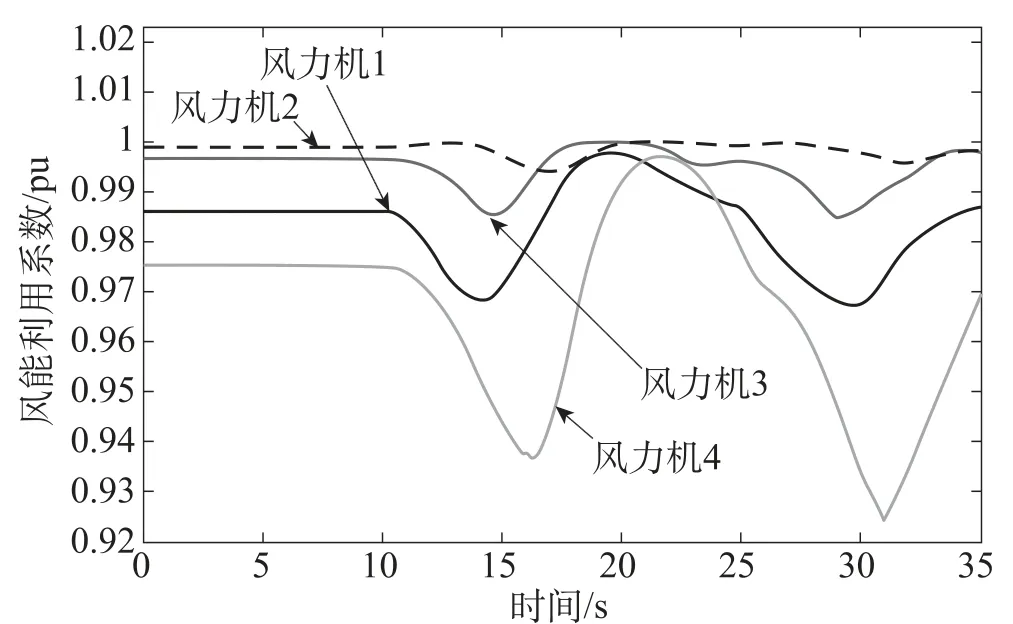
图5 各台风力机的风能利用系数
由图4~图6可知,当各台风力机处的风速存在一定的偏差时,所述的功率输出控制算法计算出的各台风力机的风能利用系数标幺值均在0.9以上,其中风力机4的风能利用系数较低,这是鉴于风力机输出功率为风速的三次方,尽可能使风速较高的风力机获得较好的风能利用系数,从而使发电机输出更多的功率,即可从整体上提高风电场的风能利用率。
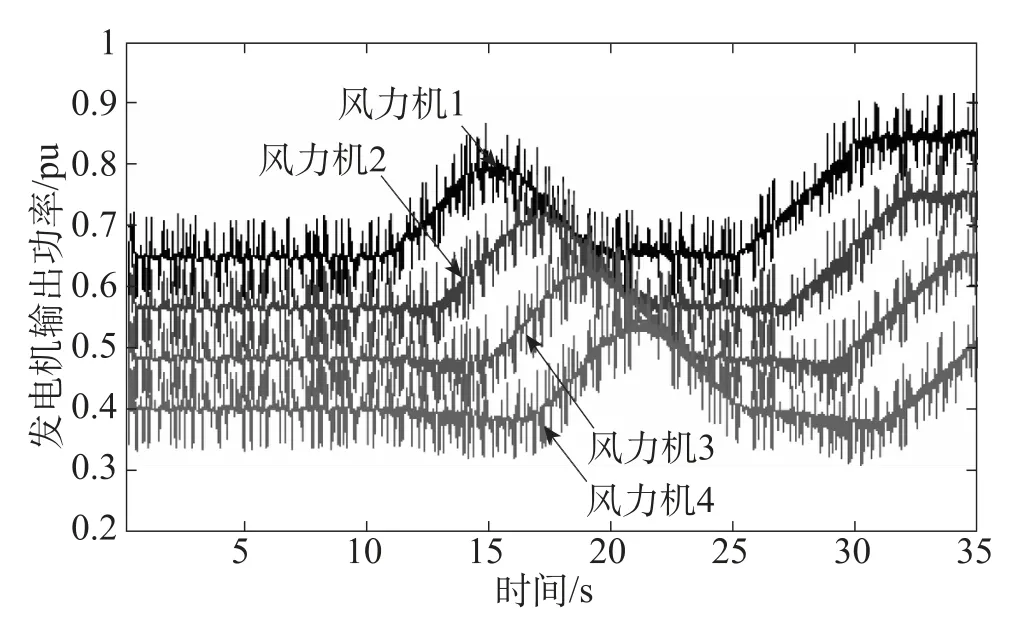
图6 各台发电机的输出功率
图7给出了四组高风速,实时计算的仿真结果如图8~图10所示。
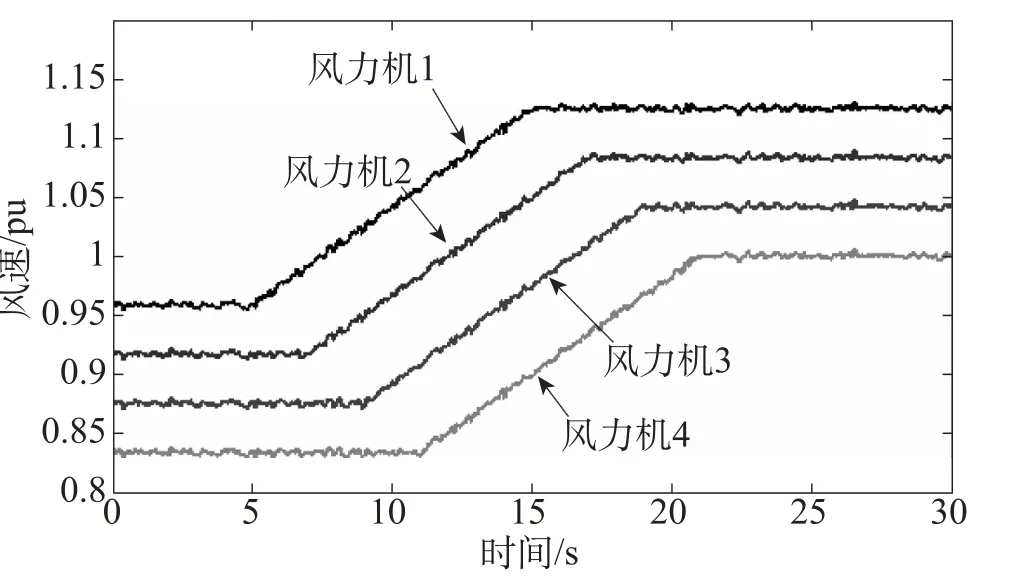
图7 各台风力机处的风速
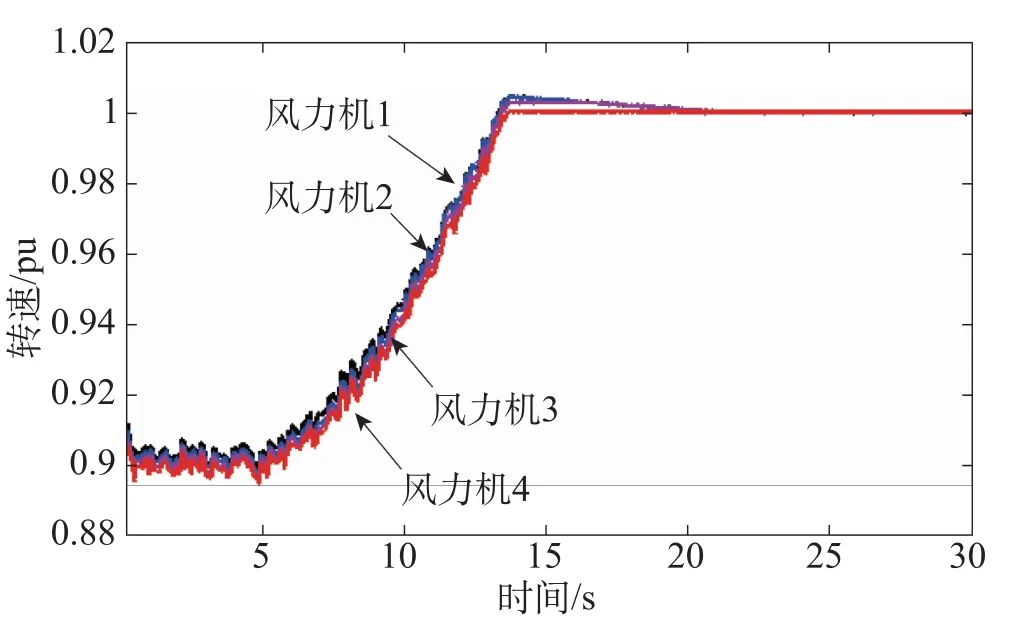
图8 各台发电机的转速
图8为各台发电机的转速,可见同一条变频交流母线上各台发电机组的转速基本一致,存在细微差异的原因是由于各台风力机处的风速存在差异,各台风力机的输出力矩不同导致。当风速超过额定转速时,各台发电机的转速运行于额定值。对于风速过高的风力机,可通过桨距角的调节作用,如图9所示,控制其运行于恒功率发电模式,如图10所示。对于图6、图10所示的发电机输出功率波形存在的针刺波动现象,这是由于受风速湍流的影响,实时计算得出的发电机转速也跟随波动上下变化,风力机捕获的风能与发电机的旋转动能之间相互转化,这是无法避免的。
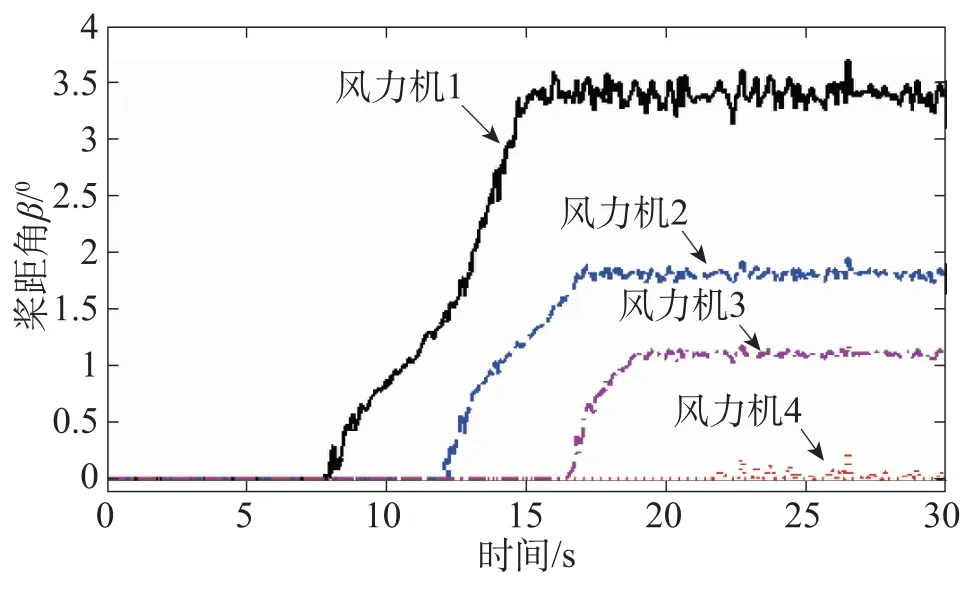
图9 各台发电机的转速

图10 各台发电机的输出功率
5 结束语
本文提出了一种基于集中式变流器的风电机群功率输出控制方法,在低风速时,忽略桨距角的调节作用,将各台风力机的风能利用系数公式简化为叶尖速比λ的多项式,进而将公式简化求导求解最佳的风电机群同一转速。对于风速过高的风力机,利用桨距角的调节作用使其运行于额定功率。仿真结果表明,所提出的功率输出控制算法在一定程度上减少了风电机群集中控制所带来的风能损失,且能够控制风速过高的风电机组运行于恒功率发电模式。
