面向振动信号的滚动轴承故障诊断算法综述*

李军宁，罗文广，陈武阁

(西安工业大学 机电工程学院，西安 710021)

轴承作为国民经济中机械行业的基础，在某种程度上其发展水平代表整个国家机械行业的发展程度。在现代国民经济中，滚动轴承被誉为“工业的关节”[1]。滚动轴承因为其显著的性能特点和优势被广泛地应用于工业的生产生活中，例如航天航空、发动机、车床、电机、雷达、船舶以及各种矿山机械、农业机械、轻纺工程、仪器仪表工程等[2]。滚动轴承良好的运行状态对于整个设备的平稳运行起着至关重要的作用。同时，滚动轴承在使用过程中会随着运转时间的增加极可能会出现疲劳剥落、磨损、腐蚀和断裂等故障，对机械设备的正常运转造成影响，更加严重的还会造成人员伤亡，尤其对于那些使用在高速条件下的滚动轴承所出现故障概率会更高，危害更大。所以对于滚动轴承所出现的故障及时发现并做出相应的措施，非常具有实用价值，已经成为当代研究领域的一个热点问题。

近年来，对于滚动轴承的故障诊断方法如雨后春笋般不断涌现和发展。总体来说，滚动轴承的故障诊断技术有：基于振动信号、声信号、电信号[3]和温度信号等方式。其中以振动信号的应用更加广泛和普遍，也更加直观和简单[4]，因为其最能表征轴承运转过程中的故障特征信息。从故障诊断的流程出发，滚动轴承故障诊断的过程大体分为数据的采集并处理、故障特征提取和故障特征识别三个阶段。

文中主要是针对滚动轴承故障诊断的各种常用算法从数据预处理、故障特征提取和故障特征识别三个方面进行论述，并对典型故障诊断综合方法进行对比分析，验证了算法的可行性。

1 数据预处理研究

在实际工作环境中，获取的滚动轴承故障特征信号多为非平稳序列信号，无法避免含有较大程度的噪声，掩盖原有故障特征信号。为准确获取滚动轴承故障特征信号，降低噪声、提高信噪比，需对其进行数据降噪预处理。同时，选取的数据降噪方法也应该与后续特征提取和特征识别相结合，综合考虑才更加有效。常见的数据预处理方法有：小波阈值降噪、经验模态分解(Empirical Mode Decomposition,EMD)、奇异值分解(Singular Value Decomposition,SVD)、滤波去噪等[5-8]。

1.1 基于小波阈值的降噪预处理

小波具备较高的适应性，在时间尺度上对高频信号敏感；而在频率尺度上对低频信号敏感。小波降噪的方法有许多种，其中最常用的是小波阈值降噪，具有简单、有效性的特点。文献[9]提出了小波阈值降噪的基本方法为分解过程、阈值处理过程和重构信号，如图1所示。

根据前文中国35个大中城市地价、房价和物价的收敛性分析结果可知，2010年之前各城市的地价呈现σ发散现象，而在2010年之后才有了一定的收敛趋势。此外，2010年之前我国房价不断持续高涨，2010年中央政府出台了一系列房地产调控政策，从抑制需求、增加供给、加强监管等方面对房地产市场进行全方位调控，进而抑制房价过快上涨。增加住房供给无疑又冲击了土地市场，引发北京等热点城市频现“地王”。因此，本文以2010年为分割点，将样本期2002—2016年划分为2002—2010年和2010—2016年两个时段进行实证检验，以考察地价、房价和物价三者之间互动关系的时序差异。估计结果如表6所示：

图1 基于小波阈值降噪的流程

2013年，文献[10]采用改进的小波阈值降噪方法对滚动轴承振动信号进行降噪预处理，综合运用了软、硬阈值函数的优点，并验证了去噪方法的有效性和保证了故障特征的提取。2015年，文献[11]提出了一种正交小波优化阈值降噪的方法，有效的降低了信号中的噪声干扰。2017年，文献[12]提出了改进的小波阈值算法进行降噪处理，采用小波能量熵与小波阈值相结合的方法，可以很好的滤除掉故障信号中的噪声。2019年，文献[13]针对带有大量外部环境噪声的信号，采用非线性小波阈值方法来去除包含噪声的信号分量；文献[14]提出一种基于小波包阈值降噪的方法，可以有效的抑制噪声，提高信号的处理精度。2020年，文献[15]为削弱噪声对轴承有效故障特征信号的影响，提出了一种小波包多阈值的方法对其进行降噪处理；文献[16]提出小波阈值降噪方法有效的抑制噪声信号，并且获取了最佳的小波基和分解层数；文献[17]基于小波软阈值函数进行去噪，利用Matlab中的Wden函数验证了去噪的效果，表明了小波软阈值降噪的有效性，并保留了故障信号的成分，为后续的特征提取奠定基础，对比效果见图2。2021年，文献[18]提出了一种新小波阈值的降噪方法，为达到最优信噪比，采用计算每层分解的数据和原始数据的相关系数，改变阈值调节因子，在不同的分解层选取阈值函数的方法，增强了新阈值的灵活性和降噪效果；文献[19]为更好地抑制噪声与保留信号的细节信息，同时以减小小波系数恒定偏差为原则，提出了一个基于双曲正切函数具有高阶可导性和自适应小波系数收缩能力的阈值函数，并且通过试验仿真验证了其自适应性和提高了小波阈值的降噪能力。

微生物品种种类多、应用范围广，并能够促进有机物料腐熟，改善农产品品质，改良和修复土壤。截至2018年9月，我国微生物肥料年产量在1600万吨，年产总值达到300亿元。微生物肥料累积应用面积3亿亩以上，应用范围包括蔬菜、果树等。微生物肥料已成为新型肥料中年产量最大、应用面积最广的品种。可以说，微生物肥料具备国家战略需求特征。

1.2 基于EMD的降噪预处理

EMD信号降噪的基本原理是通过对基本的模态分量(Intrinsic Mode Function,IMF)与原信号的相关分析去除伪分量，采用基本IMF的自相关分析方法识别噪声分量,再进行信号重构以达到降噪的目的[20]。

图2 软阈值函数降噪前后对比

2012年，文献[21]基于EMD与小波变换创建了一种新的去噪方法；为了处理滚动轴承早期故障诊断信号的信噪比比较小不易采集的问题，文献[22]提出了基于样本熵准则的EMD滤波处理噪声的方法。2013年，文献[23]采用EMD降噪的方法解决了噪声对微弱故障信号干扰导致诊断效果模糊的问题。2015年，文献[24]提出基于EMD和独立成分分析相结合的去噪法，并且通过仿真验证了信噪分离的有效性。2016年，文献[25]运用EMD滤波降噪的原理对滚动轴承振动信号进行降噪，有效的增强了滚动轴承故障诊断的效果。2020年，文献[26]采用EMD对原振动信号处理获得了一组IMF，为消除混在原振动信号的噪声对IMF进行了重构。

ρs,ci=max(Rs,ci(τ))/max(Rs(τ)),

(1)

式中:ρ为相关系数；s为原信号；ci为第i个基本IMF;R(τ)为相关性。

各自的自相关性为

(2)

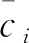
采用SPSS 18.0统计学软件对数据进行处理，计量资料以“±s”表示，计数资料采用x2检验，采用t检验，以P＜0.05为差异有统计学意义。

各IMF与原信号的相关系数为

同时，在EMD算法的基础上演化出一种集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)的去噪方法。2014年，文献[27]为了提高故障信号中的信噪比，采用EEMD对故障信号进行降噪处理。2015年，文献[28]利用EEMD分解原始故障信号得到多个本征IMF分量，并且采用峭度准则筛选出最优的IMF分量进行重构，进而实现降噪目的。2018年，文献[29]针对早期滚动轴承故障信号非平稳和噪声强等问题，提出了一种EEMD和空域相关降噪相结合的方法，有效的抑制了信号分解的模态混叠效应和故障信号噪声影响。2019年，文献[30]为减少噪声对滚动轴承故障特征提取的影响，提出了一种基于EEMD和自相关阈值降噪相结合的降噪方法。

在物质景观类，洪江古商城古商业特色显著，主要为商贸建筑与设施遗存。黔阳古城的物质景观更多地表现了古代城市的完整面貌。高椅古村和荆坪古村作为历史上纯粹的生活空间，其物质景观偏向传统乡土生活设施，高椅古村表现为各个完整院落，荆坪古村表现为以宗祠为纽带的完整村寨。

1.3 其他降噪预处理的方法

近年来，对于滚动轴承故障诊断所获取的数据信号进行预处理的方法不断更新和发展，都取得了良好的去噪效果。文献[31]利用SVD对机械设备的振动信号进行降噪处理,获得了不错的结果；为了改进SVD去噪倾向于保留能量显著的奇异分量而对于微弱的奇异分量经常会被忽略，进而会弱化诊断轴承早期故障的能力，文献[32]提出一种基于累积分量峭度的SVD重构方法来对振动信号进行降噪处理，以检测早期的故障，并通过仿真和试验分析表明比传统的方法更加有效；针对早期滚动轴承故障信号的能量小，极易受到噪声的干扰而被淹没的问题，文献[33]提出一种基于奇异谱分解(又称SVD)和独立分量分析的降噪方法，根据试验和仿真分析验证该方法满足对滚动轴承振动信号的降噪处理。文献[34]以形态滤波方法为基础，提出基于多尺度运算的平均组合形态滤波降噪方法，很好地去除滚动轴承振动信号的噪声干扰；文献[35]提出一种对变转速工况下的滚动轴承振动信号进行降噪的方法，利用分数阶傅里叶变换滤波和最小均方算法相结合，很好的降低了噪声问题；文献[36]由于信号中的噪声影响滚动轴承复合故障的诊断和分离，提出了一种基于周期性加权峰度-稀疏去噪与周期性滤波相结合的方法。文献[37]采用时频流形(Time-Frequency Manifold,TFM)的方法来处理信号，利用TMF具有强大降噪能力的优势来降低信号的噪声；文献[38]提出一种时频联合降噪的信号预处理算法，可有效的抑制信号中的噪声分量。为了解决滚动轴承获取振动信号被强烈噪声干扰的问题，文献[39]提出一种堆叠降噪自编码器(Stacked Denoising Autoencoder,SDAE)的算法，SDAE被用来处理时间序列数据与多个维度和噪声干扰的问题。

1.4 数据预处理方法对比分析

机器学习是人工智能的一个分支，它的内容已经涉及到各个领域，具体可以细分为经典的机器学习模型和深度学习模型。经典的机器学习模型常用的有ANN、DT和SVM等。近年来，深度学习作为机器学习的一部分也在不断的发展，常用的算法有卷积神经网络(Convolutional Neural Network,CNN)、自编码神经网络等。

每年的四五月份，成群结队的飞鱼便会迫不及待地来到靠近陆地、岛礁的地方，寻找适合产卵的场所。而漂浮在岸边的棕榈叶，对于它们来说是再合适不过的产卵地（海藻丛生的海域，也是飞鱼喜欢的产卵地点）。

表1 数据预处理方法的对比

2 故障特征提取方法研究

故障特征提取，是指通过变换，将高维度的原始特征空间的模式向量降为低维度的特征空间的新模式向量，进而从中找出最具有代表性和最有效的故障特征。在实际的工作环境中，滚动轴承处于稳态时，获取的振动信号多为平稳的，而当发生故障时，获取的振动信号多为非平稳的。传统的时域、频域分析方法大多是基于平稳理论提出的，比如傅里叶变换主要应用于平稳信号，对非平稳信号分析则会产生较大的误差。因此时频域特征提取方法被提出，它将时间和频率联合起来表明非平稳信号的特征随时间的变化情况[40]。常用的方法有短时傅里叶变换(Short-Time Fourier Transform,STFT)、EMD分解、希尔伯特-黄变换(Hilbert-Huang Transform,HHT)、魏格纳-威尔分布(Wigner-Ville Distribution,WVD)、小波变换、SVD等。

视听说注重培养学生语言基本功，而课堂学习认知活动中的表现最能直观反映学生的语言素质。因此，课堂学习认知活动考评尤为重要。

2.1 短时傅里叶变换(STFT)

利用遗传算法(Genetic Algorithm,GA)对VMD进行参数寻优，可获取更加精确的参数值，最终获取最小的适应度值和最佳的参数值，再重新设定VMD的分解参数，以提取到更精确的故障特征频率。在转速3 000 r·min-1时，滚动轴承内圈的理论故障频率为462.4 Hz，图4为GA-VMD分解重构后内圈故障的包络谱图，可知实际的故障特征频率为454.86 Hz和倍频谱线幅值十分突出，表明故障特征信息已被提取出。

(3)

式中:e-jωt为基函数；f(t)为时域信号；g(t)为窗函数。

2012年，早期滚动轴承故障信号能量小，频带分布广，传统的包络谱分析会在强干扰下对滚动轴承故障提取失效，文献[42]提出一种基于STFT的能量谱和独立分量分析的抗干扰滚动轴承包络分析新方法，通过试验验证了对滚动轴承故障提取的有效性。2015年，文献[43]利用STFT对振动信号进行时频分布来描述局部故障，再采用有监督的非负矩阵分解从时频分布中提取故障特征，有效提取了滚动轴承的故障特征。2018年，文献[44]提出一种STFT和卷积神经网络(CNN)相结合的滚动轴承故障诊断方法，综合考虑时域和频域信息，并结合CNN实现了故障特征的自适应提取。2020年，为了诊断变速滚动轴承的故障，文献[45]提出基于STFT和SVD相结合的无回声跟踪方法，并验证了该方法的性能。

进一步地，在第一阶段我们还向学生介绍魔方简史，让学生简单了解魔方的类别，最后还观看了魔方视频，有单手还原视频、盲拧视频，还有魔方比赛的视频。这些生动的事实激发了学生的学习动力，他们爱上了魔方。

虽然STFT可以用于非平稳信号的特征提取，但其对于不同信号的窗函数并不是很容易就能找到合适的，同时STFT的分辨率较差。

2.2 基于EMD的希尔伯特-黄变换(HHT)

HHT是由美籍华人黄谔提出的，其主要包含两个方面的内容：EMD与希尔伯特变换(Hilbert Transform,HT)。EMD可以将信号分解成由高到低的频率分量，然后对其进行HT，进而将时域转变为频域，就可以提取出含有轴承故障特征频率的成分。HHT在时域和频域中都具有较好的分辨率，并且具有自适应性。其具体的步骤[46]为：① 对原始信号进行EMD，获取一系列满足IMF条件的内模函数；② 使用HT处理内模函数，得到一系列的HT谱；③ 综合所有HT谱，取联合分布，得到信号幅值随时频的变化情况。

2014年，为提取到具有非线性、非平稳的特征信号，文献[47]采用具有自适应性的HHT方法，并引入变体能量法来减少分解信号中的计算量，该方法有效的诊断到滚动轴承的故障类别，并且发现故障规律是振动信号故障特征频率幅值随负载的增加而变化的趋势；文献[48]利用HHT、SVD和Elman神经网络相结合用于处理变工况下滚动轴承的故障诊断精度问题，通过试验表明该方法可以有效地对不同工况下的故障模式进行高精度分类。2016年，针对EMD存在的端点效应和虚假IMF问题，严重干扰了HHT方法的诊断精度，文献[49]提出基于改进的HHT能量熵和SVM相结合的诊断方法，并证明为滚动轴承故障诊断提供了一种切实可行的方法。2017年，文献[50]提出一种改进的HHT方法，将其与卷积神经网络相结合，该方法有效解决了振动数据耦合程度高、数据特征提取困难和故障特征识别模型难以建立的问题。2018年，针对传统HHT故障特征信息提取受到EMD模式混淆问题的限制，文献[51]提出ESMD(极点对称模态分解)方法，提高了滚动轴承故障特征提取的精度，将ESMD与HT相结合，结果显示要优于其他传统算法。2021年，文献[52]提出VMD-HHT边际谱方法，用于处理滚动轴承非线性、非平稳的振动信号，进行故障特征的分量提取，并证明该方法在特征提取方面具有良好的表现。

2.3 魏格纳-威尔分布(WVD)

WVD是典型的二次型时频表现形式,其本身满足大部分所期望的数学性质,并且有较好的时频分辨率和聚集性，但WVD也存在交叉项，产生虚假信号的问题，影响诊断的准确性[53]。信号s(t)的WVD可定义为

经过探索性因子分析，科学公信力的七个指标采用主成分因子法，可以提取一个公因子，KMO值也达到非常理想的水平，其因子负荷矩阵如表4所示。统计结果显示，每个构成变量的因子负荷值基本都高于0.6，这意味着七个变量的内涵有较大的共同度，能够作为衡量某个隐藏变量的指标。

(4)

式中:z(t)为s(t)的解析信号；t为时域变量；f为频域变量。

“政银企户保”模式下资金池内资金，作为贫困户贷款的担保金、还款的缓冲金、金融机构的激励金，“一金”抵“三金”，发挥贷款担保、损失缓冲和激励放贷三重功效，明确政府主导作用，解决传统小额信贷模式下贫困户贷款抵押担保难、贷款风险过大、金融机构贷款积极性低等难题。

2012年，对滚动轴承故障信号的非平稳、非高斯的问题，文献[54]提出了基于伪Wigner-Ville分布的滚动轴承内、外圈故障诊断方法，通过对WVD进行加窗处理，有效的抑制了交叉项的影响，并提取到轴承的故障特征信息。2014年，文献[55]提出一种基于EMD和平滑伪WVD谱熵的诊断方法，用于提取不同工作状态下的滚动轴承故障特征信息，提高了诊断的精度。2016年，文献[56]结合局部均值分解(LMD)和Wigner高矩谱(WHOS),提出了一种轴承故障诊断方法,与WVD方法进行对比，结果表明该方法保留了LED和WHOS的优点，同时也有效抑制了WVD谱中出现的交叉项效应。2019年，针对传统的EMD-WVD方法在提取时频图像信息不充分的问题，文献[57]提出基于CEEMD-WVD多尺度时频图像的滚动轴承故障诊断方法，并通过试验表明该方法具有较强的自适应性，故障识别率高，诊断的准确率达到99.75%。

2.4 基于CEEMDAN和VMD的故障特征提取

所建立的故障诊断方法在特征提取方面，分别采用了两种基本算法：自适应噪声的完备经验模态分解(CEEMDAN)和变分模态分解(Variational Model Decomposition,VMD)。

为准确识别轴承故障，应准确的提取到轴承的故障特征向量。CEEMDAN是在EEMD的基础上进行的特征提取，但会产生虚假的IMF分量，因此采用相关系数和方差贡献率结合对分解后的有效的特征分量进行提取，图3为轴承内圈故障的相关系数与方差贡献率。从图3可知，前6阶的IMF含有主要的故障特征信息，因此采用前6阶作为提取的特征向量，其他的作为虚假分量去除。

2017年，为提取噪声信号中微弱的故障特征信息，文献[58]提出一种基于CEEMDAN的滚动轴承故障诊断新方法，经诊断结果证明该方法可以更好地揭示轴承的故障特征信息，获取更准确的IMF分量。2019年，针对传统的特征提取方法无法准确的识别滚动轴承早期的故障特征频率，文献[59]提出基于CEEMDAN和改进的自适应欠阻尼随机共振(AUSR)相结合的方法，分析结果表明该方法可以显著增强故障特征频率，并证明了在工程应用中的有效性和优越性。2020年，对于在传统方法难以处理非线性振动信号的条件下故障诊断效果较差的问题，文献[60]提出基于角域重采样的变工况下轴承智能故障诊断方法，对角域信号利用CEEMDAN进行去噪与重构，结果表明该方法可以有效的诊断可变条件下的轴承故障，提高了诊断的准确率。

图3 内圈故障相关系数与方差贡献率

短时傅里叶变换也称为窗口傅里叶变换，是在傅里叶变换的基函数前乘上有限长度的窗函数，基函数起到限频的作用，窗函数起到限时的作用，以此来对信号进行时频局部化分析[41]，数学表达式为

2016年，针对滚动轴承振动信号的非平稳、非高斯特征，文献[61]提出一种基于变分模态分解(VMD)和自回归(AR)模型参数的故障特征提取方法，验证了该方法故障诊断的有效性和优越性。2017年，针对滚动轴承早期故障振动信号提取困难的问题，文献[62]提出了一种基于VMD和随机共振(QPSO-SR)去噪的提取方法，采用VMD对去噪后的信号进行分解，实现对微弱故障信号的提取，提高了噪声背景下VMD的计算精度。2019年，文献[63]提出了一种基于最优VMD的新方法来提取滚动轴承故障特征，采用鲸鱼优化算法优化VMD，并经过对比表明了该方法的有效性。2020年，对于早期滚动轴承的振动信号是非线性、非平稳的，故障信号微弱且难以提取的问题，文献[64]提出基因突变粒子群优化变分模态分解(GMPSO-VMD)算法，准确的提取到轴承故障状态的特征频率。2021年，为了提取滚动轴承的非线性、非平稳的振动特征信号，文献[65]提出改进的变分模态分解(IVMD)算法，具有从分解模态中提取最优故障特征和克服噪声干扰的优点，结果表明，该方法能够提高信号的分解精度和影响参数的适应性，实现轴承振动信号的有效提取，文献[66]提出用多目标多岛遗传算法(MIGA)来优化VMD的参数,并将其应用于滚动轴承故障的特征提取，提高了故障诊断的准确率。

图4 模态分量的包络谱图

2.5 基于其他方法的故障特征提取

除了上述的时频域故障特征提取外，还有一些其他类型的故障提取方法，也取得了不错的效果。2013年，基于独立分量分析(ICA)和倒谱的优点，文献[67]采用改进的ICA和倒谱分析滚动轴承故障特征提取方法，实现了弱故障的有效提取。2014年，为了从滚动轴承复杂的振动信号中提取微弱的故障信号，文献[68]将递归最小二乘格子阶梯算法引入，提出一种自适应特征提取方法。2016年，为了提取轴承的非平稳和非线性特征，文献[69]提出局部均值分解(LMD)和三阶累积量对角切片谱相结合的故障特征检测方法，其应用在轴承内圈的故障有效特征提取验证了该方法的有效性和实用性。2018年，为了准确地提取复杂的非周期滚动轴承的故障数据，文献[70]提出基于局部频谱的轴承数据特征提取方法，该方法减少了虚假频率的产生，并兼容了时域和频域的分析能力，在故障诊断方面具有很高的实用价值。2020年，为了解决复杂非平稳滚动轴承信号的初期故障检测难度较大，干扰源成分较多的问题，文献[71]提出融合混沌理论和数学形态学的新型故障特征提取方法，采用复合多尺度形态分形维数(CMMFD)的方法从去噪的信号中提取CMMFD 特征，并通过分析模拟和试验结果，对比了不同方法的准确性和效率；文献[72]基于变工况下轴承故障难以识别和分类的问题，提出一种基于多维故障能量特性优化并结合改进的最小二乘支持向量机(LSSVM)的新方法,在详细分析小波能量特征提取的基础上，提出了多维故障能量特征提取结合传递分量方法的协同方法,并证明该方法能够有效提取变工况下的多维故障特征。2021年，为了提取滚动轴承的潜在故障特征，文献[73]提出一种基于自学习稀疏原子和频带熵的滚动轴承潜在故障成分特征提取方法，将自学习稀疏原子方法应用于滚动轴承早期故障微弱的振动信号，取得了不错的成效；针对早期轴承故障特征频率提取困难，文献[74]提出一种自适应特征提取方案，采用自适应复合量子形态分析方法，对信号进行自适应解调分析，最后提取包络谱中的故障特征，结果表明该方法表现良好；文献[75]提出一种新的指标和周期增强群稀疏(PEGS)模型，用于滚动轴承的早期故障提取，该模型可以提高故障信号的稀疏性和提取故障特征的能力；为了提取足够有效的轴承信息，文献[76]提出一种新的提取方法—多尺度一维混合模式(1D-HBP)，用于滚动轴承的故障诊断，该方法用于提取故障信号的局部和全局的纹理统计信息以反映轴承的情况，并验证了所提出的诊断模型的有效性和实用性。

2.6 故障特征提取方法对比分析

对常用的几种时频域故障特征提取方法：STFT、HHT和WVD，和两种优化算法：CEEMDAN与VMD，从主要原理、应用难点和应用场合方面进行比较见表2。

最小二乘支持向量机(Least Squares Support Vector Machines,LSSVM)是在SVM算法上进行的改进，大大提高了其解算的效率。2017年，对于出现在滚动轴承故障诊断中的多故障识别与诊断的困扰，文献[90]采用多核的LSSVM算法对滚动轴承进行分类识别和诊断，结果表明该方法具有更好的故障识别率。2019年，为了从原始的振动数据中自适应地提取滚动轴承的固有故障特征，文献[91]提出深度堆叠的LSSVM算法，识别不同的故障类型，不同算法的识别准确率效果如图5所示。2021年，为了解决非平稳、非线性的振动信号对诊断精度的影响，文献[92]采用多尺度模糊熵获取特征向量，将其输入到LSSVM进行故障识别，试验结果证明该算法的识别精度达到97%。

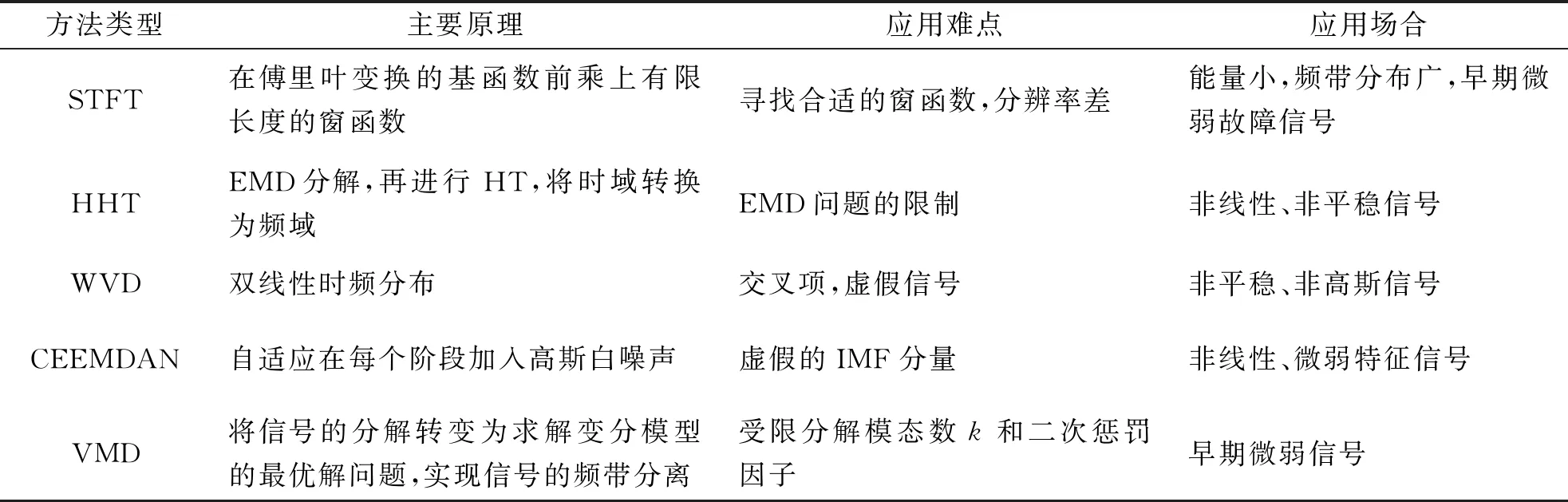
表2 故障特征提取方法的对比

3 故障特征识别方法研究

在进行完滚动轴承故障提取后要实现故障状态的识别，如今随着机器学习和人工智能的不断发展，越来越多的研究者将轴承故障诊断与此相结合起来。常用故障识别方法有深度学习(Deep Learning,DL)、人工神经网络(Artificial Neural Network,ANN)、决策树(Decision Tree,DT)以及支持向量机 (Support Vector Machines,SVM)等。同时，近年来各种智能优化算法层出不穷，如粒子群算法(Particle Swarm Optimization,PSO)、鲸鱼算法(Whale Optimization Algorithm,WOA)、蚁群算法(Ant Colony Optimization,ACO)、遗传算法(Genetic Algorithm,GA)、免疫算法(Immune Algorithm,IA)和禁忌搜索算法(Tabu Search or Taboo Search,TS)等，不断与其他算法相结合和改进也取得了不错的效果。

对应用在滚动轴承故障诊断的常用几种数据预处理方法从主要原理、优缺点和应用场合进行比较，见表1，主要有小波阈值降噪、EMD分解降噪、EEMD降噪、SVD降噪和形态滤波去噪。

3.1 基于经典的机器学习算法故障识别

ANN的结构经常由经验决定，其识别精度与训练样本的数量有关。其中，误差反向传播(Back Propagation,BP)算法是ANN中最常用的一种算法。2017年，文献[77]为提高BP神经网络的诊断效率，提出改进的BP神经网络算法Levenberg-Maquardt算法。2019年，针对故障振动信号含有剧烈噪声，故障特征难以识别的问题，文献[78]采用SVD去噪、EEMD分解，并将归一化后的故障特征参数作为BP神经网络输入参数进行轴承故障诊断，通过试验证明该方法可以有效识别滚动轴承的故障类型。2021年，文献[79]提出基于修正的傅里叶模态分解(MFMD)和多尺度置换熵的故障提取新方法，并结合BP神经网络对故障模式识别进行了研究，经试验表明该方法对不同类型的故障具有较高的识别准确率，达到98%以上。

DT对节点数据样本测试，并依据结果的不同划分数据集，DT的分支过多会导致过拟合现象。2016年，针对滚动轴承的混合故障诊断问题，文献[80]采用小波包能量与决策树算法相结合，利用小波包能量进行故障提取，然后用决策树模型进行故障的识别分类，试验表明该方法具有原理简单、准确率高的优点。2017年，为更好的识别出故障的类型，文献[81]提出一种包络样本熵和决策树门限值自适应调节算法相结合的算法，采用决策树自适应调节门限值来准确诊断出故障类型，经结果表明该算法可以有效的提高故障的识别率，综合识别率达到96.75%。2020年，针对滚动轴承故障诊断率不高的情况，文献[82]提出小波包分解和梯度提升决策树(GBDT)的方法，将提取到的故障特征数据集，输入到梯度提升决策树分类模型中进行故障诊断，采用凯斯西储大学轴承测试数据进行验证，表明该算法具备良好的故障识别能力。2021年，文献[83]采用正则化逻辑交替决策树(RLADTree)算法进行智能识别滚动轴承的故障状态，提高了故障诊断的精度与效率。

SVM是一种小样本模式分解方法，将低维线性不可分转变为高维线性的可分数据，并用最优超平面使间隔最大化[84]，其具备适应性强、效率高、全局性强等优点。2017年，文献[85]利用尺度不变特征变换(SIFT)和核主成分分析(KPCA)进行故障的提取，并结合SVM分类器以实现故障的分类，结果表明该方法的故障分类精度较高。2019年，文献[86]将SVM应用到滚动轴承的故障状态识别当中，取得了良好的效果；文献[87]采用SVM算法对提取后的数据进行故障诊断，试验表明其保证了较高的故障识别能力。2020年，为改进SVM的参数过多和局部最优解的问题，文献[88]提出单形进化算法优化SVM的滚动轴承故障诊断方法，结果表明该方法有效的完成了故障信号的诊断与识别。2021年，针对滚动轴承的故障诊断精度低的问题，文献[89]采用小波包变换、主成分分析和SVM相结合方法，结果表明可以有效地识别出不同故障位置的故障程度。

治山治水治穷 建设生态家园——四川省坡耕地水土流失综合治理试点工程建设纪实…………………………………………………………………… （20）

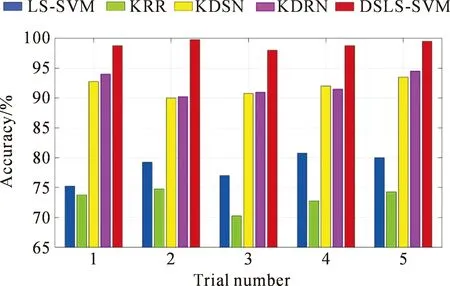
图5 不同算法准确率对比效果

3.2 基于智能优化算法改进SVM的故障识别

其他常用的智能优化算法优化SVM如下。2017年，文献[93]通过遗传算法(GA)优化SVM，以实现故障特征的分类，根据凯斯西储大学轴承数据进行试验，结果表明对七个类别的故障特征分类准确率为99.75%。2018年，为解决常用的故障分类框架中一般使用单域特征分类器模式，容易导致识别的准确率低等问题，文献[94]采用PSO优化SVM，实现滚动轴承多故障状态的识别。2019年，文献[95]采用灰狼优化算法(GWO)对SVM的核函数参数进行全局优化，进而使SVM达到最佳的分类性能，提高分类识别的准确率。2020年，针对轴承振动信号混合噪声对有用信息提取的影响，文献[96]提出基于多尺度排列熵和布谷鸟搜索算法(CS)的故障诊断优化分类器，采用CS对SVM的全局最优解进行优化，集成故障识别率高达90%。2021年，针对传统智能算法优化SVM时容易出现局部最优值、寻优速度慢和调节参数多等问题，文献[97]采用麻雀搜索算法(SSA)对SVM的惩罚因子和核函数参数进行优化，研究表明该方法可以以较高的准确率识别出故障信息，且分类性能较好；文献[98]提出基于量子行为粒子群优化算法(QPSO)、多尺度置换熵和SVM的方法构建故障特征集，实现滚动轴承的故障识别，识别准确率可以达到95%。

图6 PSO-LSSVM模型诊断

图7为滚动轴承无故障、内圈故障和滚动体故障三种不同故障状态下的混淆矩阵结果，根据最终的测试结果表明其识别精度可以达到97.14%。

品种始终是提高蔬菜产品质量及产品竞争力最有效手段。要尽力推广使用优良新品种。积极与国内外知名种苗公司合作，引进推广优质新品种。引种原则：兼顾生产者、经营者和消费者三方的利益。要让品种使用的生产者认可，适合当地的气候条件，抗性强，便于田间管理，高产优质。其次，要让蔬菜产品经营者认可，产品耐贮、耐运，质量优异，售价高。第三，还要让消费者认可，产品商品性好，符合消费习惯。

本研究采用两种智能算法优化LSSVM进行滚动轴承的故障识别。一种是采用粒子群算法(PSO)对LSSVM进行系统优化，很好的避免了参数设置的随机性，其最终的诊断结果见图6，可知其识别精度为95.71%。另外一种是用改进的鲸鱼优化算法(VNWOA)优化LSSVM，其中采用冯诺依曼拓扑结构对鲸鱼算法改进，提高了全局的最优解和收敛精度。

图7 VNWOA-LSSVM混淆矩阵

3.3 基于深度学习算法故障诊断

作为具有多层架构的深度学习模型，CNN主要是依赖于自主学习[99]，CNN典型的架构包括卷积层、池化层和全连接层[100]，它的基本结构如图8所示。

b.Shefelt a flood of relief.（Halliday&Matthiessen 1999：232）

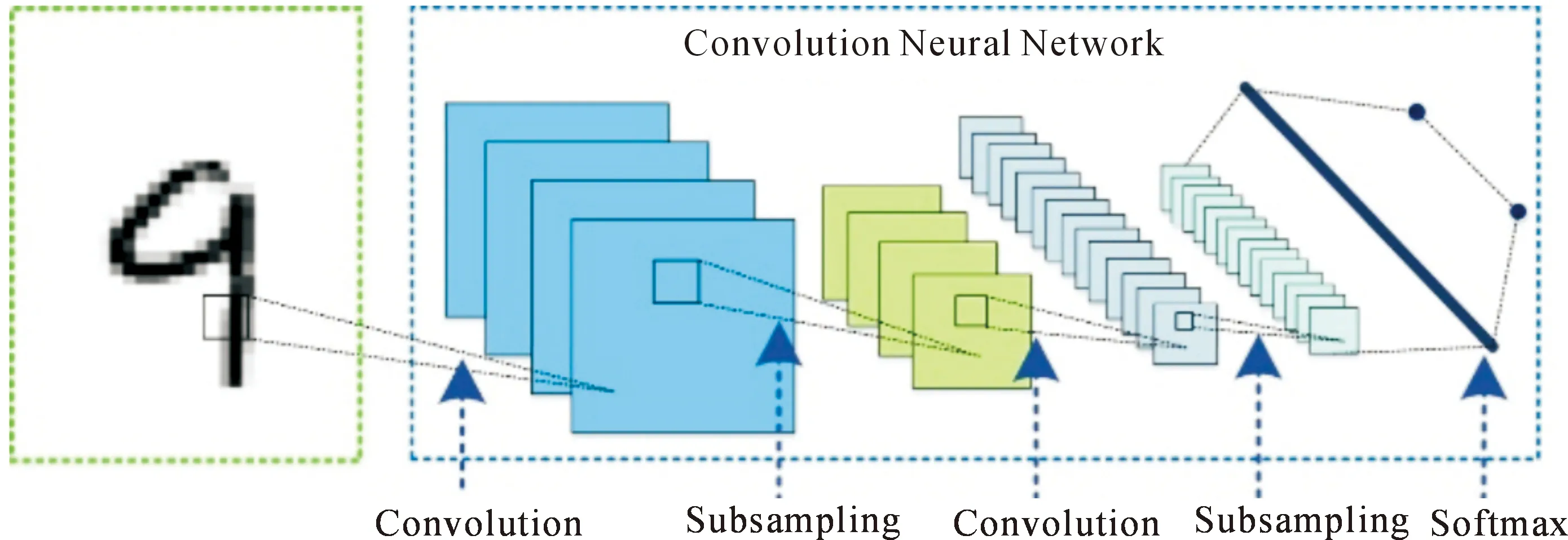
图8 CNN的结构

2019年，针对滚动轴承在不同转速下工作，导致了其故障特征提取困难，文献[101]提出在CNN的损失函数中加入冗余属性投影，从原始数据中学习故障特征，结果表明该算法具有更高的精度和更简单的框架；为了解决传统的智能诊断模型鲁棒性差的问题，文献[102]提出采用多维输入的CNN进行故障诊断，提高了识别的精度和抗干扰的能力。2020年，针对滚动轴承工况复杂多变，传统的算法适应性较差和信号处理依赖于人工特征提取与专家经验的问题，文献[103]提出一种基于“端到端”的一维CNN故障识别算法，经试验表明该方法具有99%以上的识别准确率，同时可以诊断出故障的损伤程度；为解决传统CNN在不稳定和复杂的工况下性能不佳的问题，文献[104]开发了一种改进的多尺度CNN与特征注意机制(IMS)相结合的方法，在工况变化时的识别准确率见图9，可以看出该算法的准确率还是较高的。2021年，为了提高故障诊断的效率和准确性，文献[105]提出改进的具有多尺度卷积核的深度CNN，实现滚动轴承的智能故障诊断；针对多工况下工作轴承的动态变化，导致获取的振动数据不足，文献[106]设计了一种可变形CNN、深度长短期记忆和迁移学习的新故障诊断方法，根据试验表明该方法可以有效的识别出新工况下的滚动轴承故障类型。

自编码器(Auto-Encoder,AE)是一种由三层神经元组成的无监督学习方法[107]，其结构如图10所示。

按照铅锌矿的充填集料应用工艺落实效果分析，将其整体的充填集料应用进行了优化设计，整个优化设计中，将-3cm尾矿砂，冶炼水淬渣作为整个集料充填中的材料应用，并且按照对应的充填集料控制需求，将整体充填工艺应用中的材料控制做出了优化，借助这种充填材料的优化控制，能够将整体矿产充填开采工艺实施好，对于保障该矿产的开采能力提升具有重要性保障意义。结合具体的矿产充填工艺开采现状，将对应的充填集料中的材料应用膏体性能进行了分析，对应的材料性能分析如表1所示：

2018年，文献[108]提出一种深度小波自动编码器(DWAE)和极限学习机(ELM)相结合的新方法，用于滚动轴承的智能故障诊断，DWAE用于增强无监督特征学习能力，ELM识别不同的故障类型。2019年，针对在变转速变负载下对滚动轴承的故障诊断影响较大的情况，文献[109]提出基于TCO谱和堆栈AE的新型诊断方法，诊断结果表明其识别准确率达到95.72%，高于其他对比方法。2020年，为提高复杂工作条件下深度自编码器(DAE)的性能，文献[110]提出采用布谷鸟搜索算法优化DAE的新诊断方法，可以有效的区分滚动轴承在不同工况下的故障类别和严重程度。2021年，为增强DAE的特征提取能力，文献[111]提出增强的深度自编码网络算法，提高了故障特征提取的稳定性和对变工况下振动数据的识别精度。

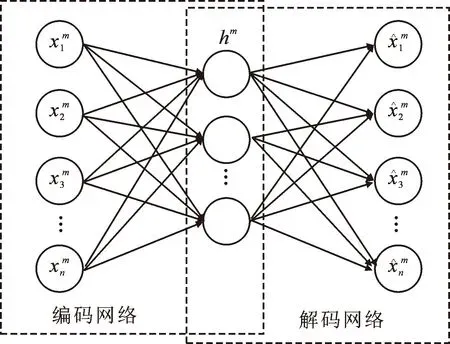
图10 AE模型的结构

3.4 故障特征识别方法对比分析

针对上述经典机器学习算法：BP、DT、SVM与LSSVM，智能优化算法改进SVM和深度学习算法：CNN与AE，从主要原理、应用难点和应用场合方面进行比较，见表3。

表3 故障特征识别方法的对比

4 典型故障诊断综合方法结果对比

为了验证所构建方法对高速滚动轴承故障诊断效果要比其他经典的故障诊断方法更加良好，进行了不同算法的综合性能对比研究，其中所列举的故障诊断算法都是经过小波阈值降噪后进行的数据处理。分别从两种所构建的故障诊断方法出发进行对比分析，一种是基于小波阈值降噪-CEEMDAN能量熵-PSO-LSSVM故障诊断方法，另一种是基于小波阈值降噪-GA-VMD-VNWOA-LSSVM故障诊断方法。

在所获取的数据中任意选取210组能量熵作为训练集，70组当作测试集，不同方法的对比效果的结果见表4。从表4中可以看出，所构建的CEEMDAN能量熵-PSO-LSSVM故障诊断方法无论从训练精度还是测试精度方面都要高于其他两种算法，其平均诊断效果可达到95.18%，而且它的训练均方差较小，可以说明所提出的高速滚动轴承故障诊断方法的有效性和优越性。

表4 不同算法综合性能对比

为了体现优化的VMD和改进的WOA算法可以有效的实现高速滚动轴承故障诊断，选取相同的样本数据进行不同算法的对比研究，其对比结果见表5，其中为了使获取的结果更加精准，表5中的结果是每种方法做10次重复试验的平均值。从中可知，利用GA对VMD进行参数寻优，可以有效的提取到轴承的故障特征信息；同时改进的鲸鱼优化算法也明显地提高了LSSVM的识别精度，其平均故障识别精度达到97.00%，可以对轴承的不同损伤部位和损伤程度得以有效的识别。综合可以看出该方法具有较高的故障诊断效率。

表5 不同算法综合性能数据对比

5 结 语

1) 在所构建的两种滚动轴承故障诊断方法的基础上，从故障诊断的基本流程出发，对主要应用在处理基于振动信号所获取数据的经典算法，从数据预处理、故障特征提取和故障特征识别三方面进行梳理，并详细论述了各种算法的主要原理、特征和应用场合，有助于推动滚动轴承故障诊断方法更好更快的发展。

2) 针对所建立的算法与经典轴承故障诊断方法进行对比分析，结果表明该方法的有效性和优越性，提高了故障诊断的准确率，有助于提升滚动轴承故障诊断方法的效率。

3) 随着数据预处理、故障特征提取和故障特征识别各方面新方法的不断丰富和融入，在提升每一方面应用效果的同时也将有效促进滚动轴承整体故障诊断技术的进步。目前，大部分故障诊断的算法常用在离线状态下的滚动轴承故障诊断，未来可聚焦于提出更加实时和智能的在线故障诊断技术，实现高速滚动轴承实时状态监测与故障诊断，以确保机械设备的安全稳定运行。对于滚动轴承的寿命预测也是未来研究热点，应不断提高和完善预测的准确性和有效性，为轴承故障的预先维修提供可靠的理论依据。