一种新型混联机构及其运动学研究

张营 张宾

摘 要：针对目前大负载并联机构工作空间小、曲面加工难度大的问题，现基于2-UPR+RPU并联机构，提出一种新型6自由度混联机构，以期能够在工业机器人加工领域得以应用。研究方法为利用并联机构逆解对混联机构整体进行运动学分析，通过MATLAB与ADAMS联合对比仿真结果的正确性。

关键词：混联机构;运动学;位姿逆解;虚拟仿真

中图分类号：TP24   文献标志码：A     文章编号：1003-5168（2022）6-0028-05

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.06.006

Research on a New Hybrid Mechanism and Its Kinematics

ZHANG Ying  ZHANG Bin

（School of Mechanical Engineering， North China University of Water Resources and Electric Power， Zhengzhou 450045，China）

Abstract：Aiming at the problems of small workspace and difficult surface machining of high-load parallel mechanism， based on 2-UPR+RPU parallel mechanism， a new 6-DOF hybrid mechanism was proposed， which was expected to be applied in the field of industrial robot processing. The research method is to use the inverse solution of parallel mechanism to carry out kinematics analysis of the hybrid mechanism as a whole. The correctness of simulation results is compared by MATLAB and ADAMS

Keywords：hybrid mechanism;kinematics;position inverse solution;virtual simulation

0 前言

工業4.0的提出，加快了制造业转型升级，一般的机床越来越难以满足柔性加工的需求。1978年，Hunt[1]首次提出把Stewart 6自由度机构作为并联机器人操作器，直到20世纪90年代初，并联机器人才引起众多学者的关注[2]。由于其在结构、刚度、载荷和精度方面的优势，使它在众多领域得到了广泛的应用，如航空航天、军工、船舶大型复杂结构件的加工。其中1T2R型并联机构的研究较为突出[3]，通常在动平台的末端添加2自由度转头，形成5自由度混联机器人，典型代表有Tricept[4]和Exechon[5]等。这使得并联机构在应用上得到了很大的改善，但是其所呈现的工作空间依旧有限。对于机构学的研究，冗余驱动并联机构具有高刚度、奇异性少的优点，典型的两类并联机构驱动冗余：在不改变并联机构机动性的前提下增加主动肢体，以及将主动关节替换为被动关节。前者提高了刚度、优化了力分配，但使机构更为复杂;后者在控制上则更加精确。其中Shin等人[6]对冗余驱动并联机构的设计和优化做出了许多贡献。贺磊盈等人[7]对一种可整周回转的新型3T1R并联机构的运动学进行了研究，并找到了奇异位型。

本研究以三条主动支链的1T2R并联机构为基础，采用新的串联方式，研究整体混联机构及其运动学，并基于并联机构运动学逆解，得到关于混联机构逆解的表现形式，利用ADAMS仿真与MATLAB理论计算对比，验证模型正确性，为后续求解工作空间及动力学分析提供依据。

1 新型混联机构构型分析

2-UPR+RPU并联机构为1T2R并联机构（其中U表示虎克副，相当于两个转动副;P表示移动副;R表示转动副），由于其对称布置，中间恰约束链在坐标系下位姿耦合，在动平台滑轨上串联可伸缩刀具构成混联机构，它的逆解简单且正解解耦方便，稳定性好。该混联机构具备两个特点：①工作空间大，且整体呈锥形，即插即用可重构;②适用于复杂的曲线、曲面加工作业。如图1所示。

1.1 机构描述

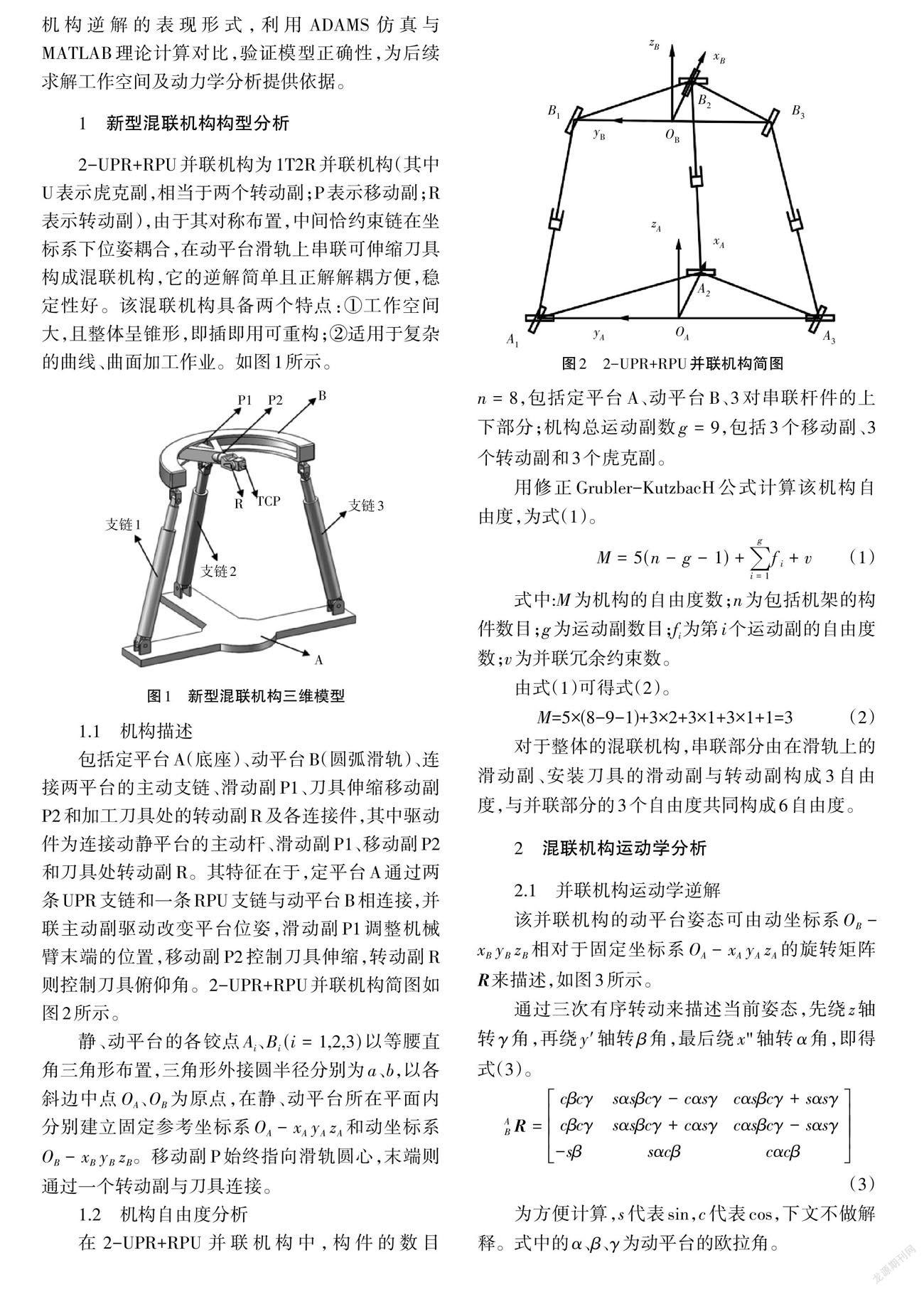
包括定平台A（底座）、动平台B（圆弧滑轨）、连接两平台的主动支链、滑动副P1、刀具伸缩移动副P2和加工刀具处的转动副R及各连接件，其中驱动件为连接动静平台的主动杆、滑动副P1、移动副P2和刀具处转动副R。其特征在于，定平台A通过两条UPR支链和一条RPU支链与动平台B相连接，并联主动副驱动改变平台位姿，滑动副P1调整机械臂末端的位置，移动副P2控制刀具伸缩，转动副R则控制刀具俯仰角。2-UPR+RPU并联机构简图如图2所示。

静、动平台的各铰点[Ai]、[Bi（i=1，2，3）]以等腰直角三角形布置，三角形外接圆半径分别为[a]、[b]，以各斜边中点[OA]、[OB]为原点，在静、动平台所在平面内分别建立固定参考坐标系[OA-xAyAzA]和动坐标系[OB-xByBzB]。移动副P始终指向滑轨圆心，末端则通过一个转动副与刀具连接。

1.2 机构自由度分析

在2-UPR+RPU并联机构中，构件的数目[n=8]，包括定平台[A]、动平台[B]、3对串联杆件的上下部分;机构总运动副数[g=9]，包括3个移动副、3个转动副和3个虎克副。

用修正Grubler-KutzbacH公式计算该机构自由度，为式（1）。

[M=5（n-g-1）+i=1gfi+v]  （1）

式中：M为机构的自由度数;n为包括机架的构件数目;g为运动副数目;fi为第i个运动副的自由度数;v为并联冗余约束数。

由式（1）可得式（2）。

M=5×（8-9-1）+3×2+3×1+3×1+1=3   （2）

对于整体的混联机构，串联部分由在滑轨上的滑动副、安装刀具的滑动副与转动副构成3自由度，与并联部分的3个自由度共同构成6自由度。

2 混联机构运动学分析

2.1 并联机构运动学逆解

该并联机构的动平台姿态可由动坐标系[OB-xByBzB]相对于固定坐标系[OA-xAyAzA]的旋转矩阵R来描述，如图3所示。

通过三次有序转动来描述当前姿态，先绕[z]轴转[γ]角，再绕[y']轴转[β]角，最后绕[x"]轴转[α]角，即得式（3）。

[ABR=cβcγ     sαsβcγ-cαsγ    cαsβcγ+sαsγcβcγ     sαsβcγ+cαsγ    cαsβcγ-sαsγ-sβ                 sαcβ                      cαcβ           ]

（3）

為方便计算，[s]代表[sin]，[c]代表cos，下文不做解释。式中的[α]、[β]、[γ]为动平台的欧拉角。

用闭环矢量法构建2-UPR+RPU并联机构的位置逆解方程，动平台参考点[OB]的向量[r=（x   y   z）T]在坐标系[OA-xAyAzA]的表达式为式（4）。

[r=αi+liωi-Rbio，（i=1，2，3）]   （4）

式中：[li]、[ωi]分别为支链[i]的杆长及其方向矢量;[bio]为点[Bi]在动坐标系下的方向矢量;[ai]为点[Ai]在静坐标系下的方向矢量。

[OBBi]可表示为式（5）。

[OBBi=R0     b    0b     0    -b0     0     0]    （5）

由机构的两个约束条件：①在[B1]和[B3]处的转动副轴线始终与平面[A1A3B3B1]垂直，②分支2的移动副轴线始终被约束在平面[OAA2B2OB]内，可以建立三个约束方程，为式（6）。

[（r-a1）TuB1=0（r-a2）TuB2=0n2y=0]     （6）

整理可得到三个结论，即[xz=tanβ]，[y=0]和[γ=0]，因此得出式（7）。

[R=ux     vx     wxuy     vy     wyuz     vz     wz=cβ     sαsβ     cαsβ0       cα       -sα-sβ     sαcβ     cαcβ] （7）

将方程写成闭环形式为式（8）。

[liwi=r-αi+Rbio]     （8）

对式两端取模后平方可得并联机构逆解，为式（9）。

[l12=（x+vxb）2+（vyb-a）2+（z+vzb）2l22=（x-a+uxb）2+（z+uzb）2l32=（x-vxb）2+（a-vyb）2+（z-vzb）2] （9）

2.2 串联部分正解

连接在动平台滑轨上的串联部分可以采用D-H坐标法对滑动副P4、移动副P5和转动副末端R建立相应的坐标系，如图4所示。

在已知滑轨与机械臂串联点时，坐标系[B]到坐标系[4]的转换需要先在[x]轴平移[x4]和[y]轴平移[y4]，此时分两种情况。

①当[y4≥0]时，绕[z4]旋转[-σ]，其中[tanσ=x4/y4]。

②当[y4<0]时，绕[z4]旋转其中[σ-π][tanσ=-x4/y4]。

此后，再绕[y4]旋转-90°;由坐标系[4]到[P]的D-H转换参数如表1所示，其中[θ]是旋转关节的关节变量，[Δd]是滑动关节的关节变量。

根据上述各连杆参数，可建立各坐标系之间的转换矩阵[B4T]、[45T]、[5PT]，令[φ=-σ，y4≥0σ-π，y4<0]，则机械臂末端相对于动平台的坐标系转换矩阵为[BTP]。

此为串联部分RP的运动学正解，分析可得：从末端坐标系[p]到动坐标系[p]，再到静坐标系[A]的转变，即[T=ARB×BTP]。

由于末端刀具采用小尺寸转动副，对机构理论分析的影响不大，故下文为简化数学模型。

令[ε]、[dp]、[θp]为0，使其更贴合实际样机，且有利于计算，规定各转角运动范围为[-45°≤α≤45°];[-45°≤β≤45°];[-85°≤φ≤85°]。

求解矩阵T得式（10）。

[T=cαsβ     sαsβsφ+cβcφ     sαsβcφ-cβsφ    Xp-sα                cαsφ                 cαcφ                  Ypcαcβ     cβsαsφ-cφsβ     sβsφ+sαcβcφ    Zp0                    0                      0                        1]

（10）

[Xp=cβx4+sφ（d+Δd）+zcαsβ+zsβ+sαsβ     y4-cφ（d+Δd）]

[Yp=cαy4-cφ（d+Δd）-zsα]

[Zp=zcαcβ-sβx4+sφ（d+Δd）-zsβtβ+sαcβy4-cφ（d+Δd）]

其中，X、Y、Z为末端点P的位置参数。

2.3 混联机构运动学逆解

在对混联机构求逆解时，机构特性参数已知，未知变量为[l1]、[l2]、[l3]、串联转角[φ]、[θp]和伸缩杆长度[Δd]，其中三根杆的长度又可以通过动平台的位姿变量[α]、[β]、[z]求得。

由串联机构几何关系得式（11）。

[x4=bsφ，y4=-bcφ]    （11）

由式（11）通过末端姿态解耦求得[α、β、φ]。

[Xp=zsβ+x4cβ-r13（d+Δd）+sαsβy4+zr11] （12）

[Yp=cαy4-r23（d+Δd）+r21z]      （13）

[Zp=-x4sβ+cβsαy4-zsβtβ-（d+Δd）r33+zr31]

（14）

联立可得式（15）。

[z=yp-cαy4+r23（d+Δd）r21]   （15）

代入得式（16）。

[Δd=]

[Xp-cβx4-sαsβy4-（sβ+r11）（yp-cαy4）/r21r23（sβ+r11）/r21-r13-d]

（16）

至此便得到所有未知变量α、β、[z]、[Δd]和[φ]，为验证所得解的正确性，将其代入式（10）与已知的[rij]以及[X]、[Y]、[Z]值对比，如果相同则说明求解正确，将α、β、[z]代入式（12）得式（16），便可得到三根杆长[l1]、[l2]、[l3]以及串联杆转动角度[φ]和刀杆伸缩长度[Δd];若不同则说明末端在该位姿下无解。

2.4 混联机构逆解验证

验证的主要思路为通过给末端规划轨迹，验证ADAMS得到的仿真曲线与MATLAB理论求解曲线是否一致。在ADAMS中建立虚拟样机，给定末端点P驱动，轨迹曲线如图5，时间设置[t=3.15 s]，离散点数[n=500]，驱动函数为式（17）。

[Xp=100sin（time）Yp=100cos（time）Zp=100sin（time）]    （17）

设动平台半径[b=300 mm]，静平台半径[a=500 mm]，单根串联杆长度[d=200 mm]，测量得到如图6（a），横坐标表示时间，纵坐标分别表示串联杆长度、串联杆转角与并联三根桿杆长。

把机构轨迹曲线的各离散点的位姿数据导出，在MATLAB中编程得到串联杆长度变化、串联杆转角变化与三根并联杆杆长变化，如图6（b）。通过对比，两者在初始与结束时长度变化，相同，在1 s处串联杆最短;串联杆转角大约在1.6 s处归零，即串联杆处于中间位置，三根并联杆的伸缩变化一致。由以上结果可以说明上述求混联逆解的方法是正确的。

3 结语

本研究提出了一种基于2-UPR+RPU并联机构的混联机构，基于逆解建立了整体混联机构的运动学逆解模型，仿真验证了模型的正确性。研究过程及结论验证了机构的可行性，为后续研究提供了理论依据。

参考文献：

[1] HUNT K. Structural kinematics of in-parallel-actuated robot-arms[J].Journal of Mechanical Design ，1983 ，105（4）：705-712.

[2] HUANG T ，LI Z X，LI M，et al. Conceptual Design and Dimensional Synthesis of a Novel 2-DOF Translational Parallel Robot for Pick-and-Place Operations[J].Journal of Mechanical Design，2004，126（3）：449-455.

[3] 何延，刘宏昭.一种三角化解耦1T2R并联机构的型综合与运动学分析[J].机械科学与技术，2019，38（11）：1669-1675.

[4] ZHANG D，GOSSELIN C M. Kinetostatic Analysis and Design Optimization of the Tricept Machine Tool Family[J]. Journal of Manufacturing Science and Engineering，2002，124（3）：725-733.

[5] 董成林，李锦涛，刘海涛，等.TriMule与Exechon机器人的切向运动传递特性同性条件及运动学性能分析[J].机械工程学报，2021，57（15）：23-32.

[6] SHIN H，LEE S，JEONG J I，et al. Antagonistic Stiffness Optimization of Redundantly Actuated Parallel Manipulators in a Predefined Workspace[J]. IEEE/ASME Transactions on Mechatronics， 2013， 18（3）：1161-1169.

[7] 贺磊盈，涂叶凯，叶伟，等.一种可整周回转的新型3T1R并联机构运动学分析[J].机械工程学报，2018，54（11）：151-160.