全球经济政策不确定性的演变趋势：基于EMD-ARIMA模型的预测分析

林赛燕

(中共浙江省委党校 数字化战略发展研究中心，浙江 杭州 311121)

一、 引 言

2008年爆发的金融危机给全球经济发展带来了巨大的冲击，各国经济政策不确定性显著加剧。为了应对因金融危机带来的不利影响，各国政府相继出台一系列宏观经济政策，由于经济形势以及各国政策的复杂多变导致全球经济政策不确定性不断上升。作为经济政策变动的风向标，全球经济政策的不确定性(Global Economic Policy Uncertainty, GEPU)是经济主体进行生产决策的重要因素，因其受关税、汇率和资本管制等国际贸易政策多重影响，进而成为影响进出口贸易和跨国投资的重要决策变量[1-3]。

随着国际贸易争端的加剧以及新冠肺炎疫情的全球性暴发，近年来全球经济政策不确定性急剧上升，世界各国为了促进本国经济增长、维持金融市场稳定，采取了一系列的应对经济政策，与此同时，应对政策波动的政策调整又反过来对各国经济的发展造成了一定程度的冲击。在此背景下，科学有效地分析和预测全球经济政策不确定性的演变特征和动态路径，对于准确把握全球经济形势和政策趋势并作出科学决策具有重要的意义。考虑到全球经济政策不确定性指数的影响因素复杂多变，其数据生成过程难以在一个时间序列模型中得到准确的体现。为了提高时间序列模型的预测精度，本文基于“先分解后集成”思想，首先采用经验模态分解(EMD)方法将GEPU指数分解为若干可读信号，其次运用主流非平稳时间序列ARIMA模型对可读信号分别进行模拟预测，最后集成各类可读信号的预测结果。

本文余下内容结构安排如下：第二部分对相关文献进行回顾；第三部分介绍了EMD分解、ARIMA模型，以及EMD-ARIMA模型的具体步骤；第四部分先通过对比ARIMA模型和EMD-ARIMA模型对于1997—2019年GEPU指数的拟合效果，以证实EMD-ARIMA模型的优势；其次通过VAR模型分析宏观经济变量与GEPU的动态关系，并进一步对VAR模型进行预测分析；最后是本文的研究结论与政策建议。

二、 相关文献综述

现有相关文献的研究主要聚焦于经济政策不确定性定量测度及其对经济增长、金融市场、国际贸易、跨国经济活动和跨国资本流动等方面的影响。由于在早期的研究中，数据难以获得，以至于早期的文献多以理论研究和定性分析为主，后期随着数据可得性的增强以及针对经济政策不确定性测度方法的提出，相关研究则以经济政策不确定性对宏观经济诸多方面影响效应的实证分析为主。

(一) 经济政策不确定性的测度及相关预测方法

学界对经济政策不确定性的测度方法主要包括三种：一是以单一经济指标来衡量[4]；二是以虚拟变量来衡量[5]；三是采用综合指数来衡量[6]。Baker等(2016)[6]提出的经济政策不确定(Economic Policy Uncertainty，EPU)指数的影响力最大，目前已被国内外许多学者广泛用于实证分析。在EPU指数的基础之上，Davis(2016)[9]构建了全球经济政策不确定性指数，该指数涵盖了全球16个主要经济体的EPU指数的加权平均值(权重为各国GDP)，较为全面地反映了全球经济政策不确定性变动趋势。由于EPU指数动态路径的影响因素复杂多变，其数据生成过程难以在一个时间序列模型中得到准确的体现，现有文献对于经济政策不确定性时间序列特征分析和预测研究鲜见报道。对于预测非平稳非线性的时间序列，Huang等(1998)[10]提出的经验模态分解(EMD)有着独特的优势。该方法能够把复杂的时间序列数据进行多尺度分解，并在生物工程领域得到广泛应用。Huang等(2003)[11]为代表的文献将EMD分解方法引入金融指数的预测分析，并使此方法在金融领域逐渐得到完善。毕星和王巍(2010)[12]集成EDM分解和平均综合模型的优势，通过构建一个混合模型对股票价格进行预测，有效地提高了预测精度。Islam(2012)[13]通过采用EMD方法对原始数据序列进行分解，同时将该方法的分解结果与小波分解方法进行对比，研究发现EMD方法相对更有效。采用EMD将经济政策不确定性指数分解成若干个具有特定规律的分量，再建立相应的时间序列模型，将在很大程度上降低建模预测的复杂性，进而提高预测精度。

(二) 经济政策不确定性与经济增长

2008年全球金融危机爆发后，在一系列经济复苏政策影响下，世界各国经济政策不确定性持续上升。在经济全球化的影响下，随着对国际依赖程度的增强和全球性问题的不断发生，各个国家(地区)所制定和实施的政策不仅会影响本国经济稳定和发展，还有可能根据经济政策不确定性特征传导至其他国家，对其他国家的经济造成一定程度的负面影响。Aizenman和Marion(1993)[14]通过实证分析验证了税收政策的不确定性会通过投资渠道阻碍经济增长，其投资的不可撤销性以及政策持续性的交互作用是产生影响的主要原因。Jones和Olson(2013)[15]研究发现EPU对通货膨胀的影响存在负面效应。针对工业生产和EPU之间的关系，实证结果显示经济政策不确定性和产出之间一直存在负相关关系。Karnizova和Li(2014)[16]通过采用衰退预测模型研究发现，对不同层面的样本数据进行分析，结果表明：EPU指数对经济衰退有一定的预测作用，进一步地证明了EPU对经济增长的影响。张玉鹏和王茜(2016)研究结果发现EPU对经济增长的影响受经济周期的影响，在经济繁荣时期，EPU对产出增长存在显著的负相关关系[17]。许志伟和王文甫(2019)发现公众对政策的预期会显著增强经济政策不确定性影响，并且劳动收入份额和劳动供给弹性的变小也会导致不断加强经济政策不确定性对经济增长的不利影响[18]。

(三) 经济政策不确定性与金融市场波动

目前，学界对于经济政策不确定性与金融市场的研究较多，研究视角和对象不同，得出的结论也会有所差异。从金融市场角度来看，由于EPU会影响投资者在资本市场投资过程中的风险承担行为，致使其减少在不确定性较高国家的风险投资，将资金从风险较高的国家转移至相对安全的国家或市场，最终表现为经济政策不确定性与股票价格之间的高度相关性[19]。Brogaard和Detzel(2015)[20]研究发现EPU的变化和股票收益率之间存在负向影响，即EPU的上升会带来股票收益率的下降。王晓娟等(2015)研究结果发现EPU与股票收益之间存在长期均衡关系，并且呈上升趋势[21]。朱孟楠和闫帅(2015)[22]、Beckmann和Czudaj(2017)[23]研究表明经济政策不确定性对汇率存在溢出效应。雷立坤等(2018)通过使用中国EPU指数数据，发现在GARCH-MIDAS模型中加入该指数后可以显著提高该模型对中国股市波动的预测精度[24]。余江等(2018)通过建立模型，分析了我国EPU对股市波动率预测的影响，研究结果发现EPU指数能够显著提高对股市波动率的预测能力[25]。Fang等(2018)[26]通过构建GARCH-MIDAS模型来检验全球经济政策不确定性对黄金期货收益率的预测作用效果。结果表明，GEPU对全球黄金期货市场月度波动率的预测正向且显著。Zhou等(2020)[27]采用GARCH-MIDAS模型研究了中美之间相对经济政策不确定性(中美EPU比率)对中国汇率波动的影响，同时比较了GARCH-MIDAS模型与传统GARCH模型的样本外波动率预测性能，研究发现中美EPU比率对中国汇率的长期波动有正向影响。李丽虹(2020)通过构建STR-GARCH-MIDAS-EPU模型，也得出了同样的结论，即该模型对股票市场波动率预测精度有所提高[28]。Su等(2019)[29]研究发现美国EPU指数与其他国家股市波动率存在正相关关系，具体来说，美国经济政策不确定性的上升会导致其他国家股市波动率上升，但Li和Peng(2017)[30]研究分析了美国EPU与中国股市之间的关系，结果表明二者存在负相关关系，即美国EPU的上升会使中国股市波动率下降。也有学者研究一国EPU指数对其他国家的股市波动的影响，发现不同国家的EPU指数对其他国家股市产生的影响存在显著差异[31]。

(四) 经济政策不确定性与国际贸易

2008年国际金融危机对国际贸易造成了巨大的冲击，导致各国制定和实施了一系列经济政策来促进国内经济复苏发展。在这一背景条件下，国内外学者开始研究EPU对国际贸易的影响。部分学者研究EPU与进出口贸易之间的关系，研究发现EPU会对企业进出入市场存在一定程度上的阻碍作用，从而影响进出口，而贸易协定能在一定程度上减弱该抑制作用[32]。一国经济政策(包括贸易政策在内)的不确定性的增强将会通过抑制固定资产投资而降低出口质量与出口价格，而降低不确定性则可以提高出口企业的产品创新[33-35]。钱学锋和龚联梅(2017)研究结果发现贸易协议能够降低贸易政策不确定性(TPU)对中国制造业企业的影响，有利于促进出口增长[36]。刘洪铎和陈和(2016)研究了EPU对来源国出口的影响，结果发现目的国EPU的急剧上升会导致来源国出口急剧下降[37]。魏友岳和刘洪铎(2017)实证检验了EPU对出口二元边际的影响效果，研究发现EPU对扩展边际具有显著的抑制效应，但对集约边际的影响则不确定[38]。陈绍俭和冯宗宪(2020)实证研究发现EPU对企业出口具有负向的影响，在考虑目的地投资环境、政府稳定性、法律秩序等因素不稳定的地区，其EPU会上升，进一步使中国减少其出口产品价值量[39]。

(五) 经济政策不确定性与跨境投资

经济政策不确定性除了对国内宏观经济产生影响之外，还会对跨国经济活动或跨国资本流动产生一定的影响。部分学者研究了EPU与外商直接投资(FDI)之间的关系，通过实证分析发现，二者之间存在显著的负相关关系，具体来说，FDI会随着EPU的增加而逐渐降低，即EPU的增加会抑制企业对外投资[40-41]。谭小芬等(2018)[42]实证结果发现全球EPU对新兴经济体资本流动具有负向的影响，即随着EPU的上升对新兴经济体资本流动的影响越小，且金融危机发生过后对新兴经济体资本流动的影响要低于金融危机发生之前。而杨永聪和李正辉(2018)研究结果发现，中国企业对外直接投资与不同国别的经济政策不确定性存在显著的差异，FDI与母国EPU之间存在正相关关系，与东道国EPU存在显著的负相关关系[43]。贾玉成和张诚(2018)通过利用跨国并购数据，实证考察了EPU对跨国并购的影响，发现二者之间存在正相关关系，即中国EPU上升在一定程度上加快了中国上市公司的海外并购活动[44]。周晶晶和赵增耀(2019)研究分析了EPU对企业投资行为的影响，研究结果发现东道国EPU对企业跨国并购规模存在显著的抑制作用，且金融危机发生之后这种抑制效果明显增强[45]。李亚波和李元旭(2019)研究发现美国EPU与中国企业跨国并购存在着显著的负相关关系，具体来说，当美国EPU提高时，中国企业将会减小海外并购的规模[46]。此外，也有少量文献从微观层面分析了经济政策不确定性与微观市场主体之间的关系，例如从企业层面研究了经济政策不确定指数与微观经济指标(如：企业投资[47-49,50-51]、企业管理[52-53]、企业杠杆率[54]以及房地产市场[55-56])等一系列的经济活动与变量之间的关系。

通过梳理相关文献发现，经济政策不确定性对现实经济活动具有多维度、多层次的影响，因此，对经济政策不确定性本身的动态变化规律的把握和研究就显得十分重要。但是现有文献对于经济政策不确定性时间序列特征分析和预测研究鲜见报道，这对于我们全面地理解经济政策不确定性，以及在此基础上做出更加科学有效的经济决策具有重要的意义，本文的研究将聚焦于此。其主要贡献是针对GEPU指数时间序列的不确定性、非线性以及不稳定性的特点，突破传统时间序列分析的单模型直接建模的思路，先用经验模态分解方法将GEPU指数分解为若干可读信号，再运用主流非平稳时间序列ARIMA模型对可读信号分别进行建模预测，最后集成各类可读信号的预测结果，为分析和预测经济政策不确定性指数的动态特征提供了新的建模思路和方法。

三、 模型与方法

GEPU指数数据具有非平稳、非线性的特点，即该指数在不确定性因素影响比较小的时候相对较低，而在发生一些重要事件(如经济波动、政治动荡、全球公共卫生安全不稳等)情况下，会引致不确定性因素的增加，进而导致该指数出现上升的趋势。为了提高对全球经济政策不确定性指数预测的准确性，本文提出经验模态分解(EMD)和自回归移动平均模型(ARIMA)相结合的方法对GEPU指数数据进行预测。EMD方法在处理各类非平稳、非线性以及复杂信号的分解方面上具有较高的优势，其对复杂的数据可进行平稳化处理，并且这种方法可以有效解决数据中存在的模态混叠问题，使其能够满足时间序列数据分析的要求。即本文用EMD将GEPU指数分解成若干个较为平稳、相互独立、频率不同的分量，再基于分量建立对应的时间序列模型，可以降低建模预测的难度，同时提高预测的准确性。本文将EMD方法与ARIMA模型合起来对GEPU指数数据进行处理及预测，将会有效提高预测的准确性。下面简要介绍经验模态分解(EMD)、自回归移动平均模型(ARIMA)以及组合模型EMD-ARIMA的建模方法。

(一) 经验模态分解

经验模态分解(EMD)方法的原理是把复杂的信号分解成若干固有模态函数分量(IMF)之和，其中每个IMF分量都必须严格具备以下两个条件：(1)对于这一序列，极值点的个数和过零点的个数必须相等或最多只能相差一个；(2)在任意时刻，由局部极大值点和局部极小值点分别形成的上、下包络线，其平均值为零，即上下包络线相对于时间轴是局部对称的。在非平稳数据中，计算局部均值是很难做到的，但使用局部极大值和局部极小值包络的平均为零代替，很好地解决了这一难题。

对任意一个信号X(t)的EMD的分解方法如下：

(1)找到信号X(t)所有的局部极大值点和极小值点，采用三次样条插值函数将极大值点和极小值点分别拟合成上、下包络线e+(t)、e-(t)。

(2)计算上、下包络线的均值，记为m1(t)。即

(1)

(3)将原始信号X(t)与m1(t)的差值定义为h1(t)，即

h1(t)=X(t)-m1(t)

(2)

(4)若h1(t)满足IMF分量的条件，那么h1(t)就是X(t)的第一个IMF分量，若h1(t)不满足IMF分量的条件，就用h1(t)替换原始数据X(t)重复(1)—(3)过程，直至h1(t)满足IMF分量的条件为止。不妨设经过k次筛选后产生第一个IMF分量c1(t)，即

c1(t)=h1k(t)=h1(k-1)(t)-m1k(t)

(3)

(5)将c1(t)从X(t)中分离出来，得到

r1(t)=X(t)-c1(t)

(4)

(6)用r1(t)替换原始序列X(t)并重复步骤(1)—(5)n次，从而得到X(t)的n个IMF分量和一个残余分量rn(t)，即

r2(t)=r1(t)-c2(t)…rn(t)=rn-1(t)-cn(t)

(5)

(7)当残余分量rn(t)为单调函数或常数时，循环停止，此时rn(t)为信号的平均趋势。

由上述分解过程不难发现，EMD分解完全是由数据自身驱动，对数据进行自适应的筛选处理，从而将原始数据X(t)分解成若干IMF和残余分量之和，即

(6)

(二) EMD-ARIMA模型

近年来，基于“先分解后集成”思想的混合模型逐渐成为时序分析与预测研究中一个主流的前沿技术。其主要思想是将“多尺度分解”步骤引入时序预测中，以从不同尺度上把握复杂系统内部错综复杂的运行规律，从而显著提高预测水平[51]。本文所引入的EMD-ARIMA模型即是“先分解后集成”思想的体现，该模型的具体步骤如下：

(1)采用EMD分解方法将非平稳数据分解为不同尺度的平稳的IMF分量。

(2)对各个IMF分量分别建立ARIMA模型进行预测，对各个时间序列都追求构建最佳滞后阶数的ARIMA模型，以达到最佳的预测效果。

(3)使用各个IMF分量的预测值重构原始数据的预测序列。

由于EMD是以线合加成的分解方式对原始序列进行分解[参考式(6)]，所以在重构方式上一般选择直接加总的形式进行集成。EMD-ARIMA模型的框架如图1所示：

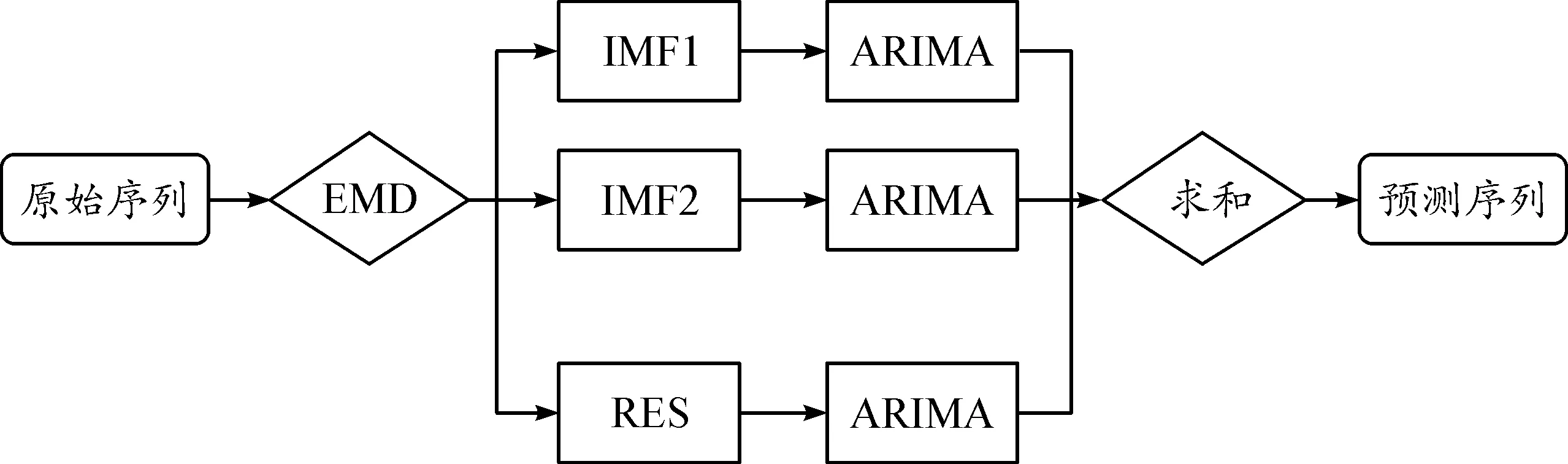
图1 EMD-ARIMA模型框架

四、 全球经济政策不确定性指数预测

GEPU指数反映了世界各大经济体经济与政策的不确定性，由于该指数与很多宏观经济指标(如经济增长和就业率等)以及国际贸易有较为显著的相关关系，所以合理预测GEPU指数对于把握宏观经济的发展以及制定国际贸易政策有重要的参考价值。

(一) 数据说明

本文数据来自www.policyuncertainty.com公布的1997年1月到2021年3月之间的GEPU指数数据，共291个样本。为了保障EMD分解后的ARIMA建模分析的可靠性，本文使用1997年1月至2019年12月共276个样本数据作为训练组建立预测模型，并使用2020年1月至2021年3月共15个数据作为测试组来检验模型样本外预测的精度。

图2为1997年1月到2021年3月的GEPU指数走势，从图中可以看出，GEPU指数呈现明显的不确定性、非线性以及不稳定性特点，这使得单一的时间序列方法无法有效对GEPU指数进行预测。本文将使用ARIMA和EMD-ARIMA两种模型分别对GEPU指数进行预测并对比预测效果，以说明在面对复杂系统的预测问题时，EMD-ARIMA模型与单一的ARIMA模型相比具有更好的泛化能力。

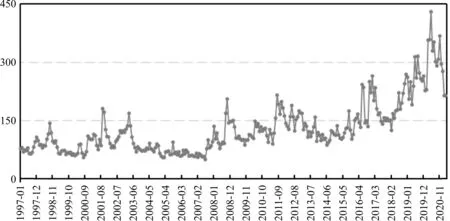
图2 1997年1月到2021年3月GEPU指数走势

(二) 实证分析

根据EMD的特点，本文在实证中直接通过MATLAB软件对原始样本数据进行了EMD分解，得到了5个IMF分量和1个残余分量，其中IMF分量根据频率由高至低的顺序依次进行排列，它们分别展示了GEPU指数序列在同一时间段内不同频率和振幅，其变换规律也略有不同，最后一个分量为趋势量，具体分解结果如图3所示。EMD将复杂的原始数据分解成若干个清晰的、周期不同的分量，在经济学分析中，可以根据不同的影响因素对各分量进行分析和解释，寻找发展规律。从图3中的IMF5分量变化趋势我们可以看出，GEPU指数呈现上涨的趋势，具体情况，待进一步建模分析。

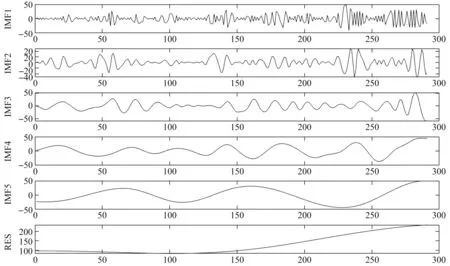
图3 GEPU指数的EMD分解结果

图3中IMF1—IMF5为GEPU指数的5个IMF分量，RES为余项。根据EMD分解结果，本文分别构建了GEPU指数、IMF分量以及RES项的ARIMA模型。在对于滞后阶数的选择问题上，本文采用AIC和SC准则来选择各个模型所对应的滞后阶数，具体模型见表1。

表1 GEPU指数、IMF分量及RES的预测模型

图4和图5分别为ARIMA和EMD-ARIMA两种模型对训练组和测试组数据的预测值与真实值的对比图，从拟合效果上来看，EMD-ARIMA模型对训练组和测试组数据的拟合精度均优于ARIMA模型。

图4 两种模型对训练组的预测值与真实值的对比图

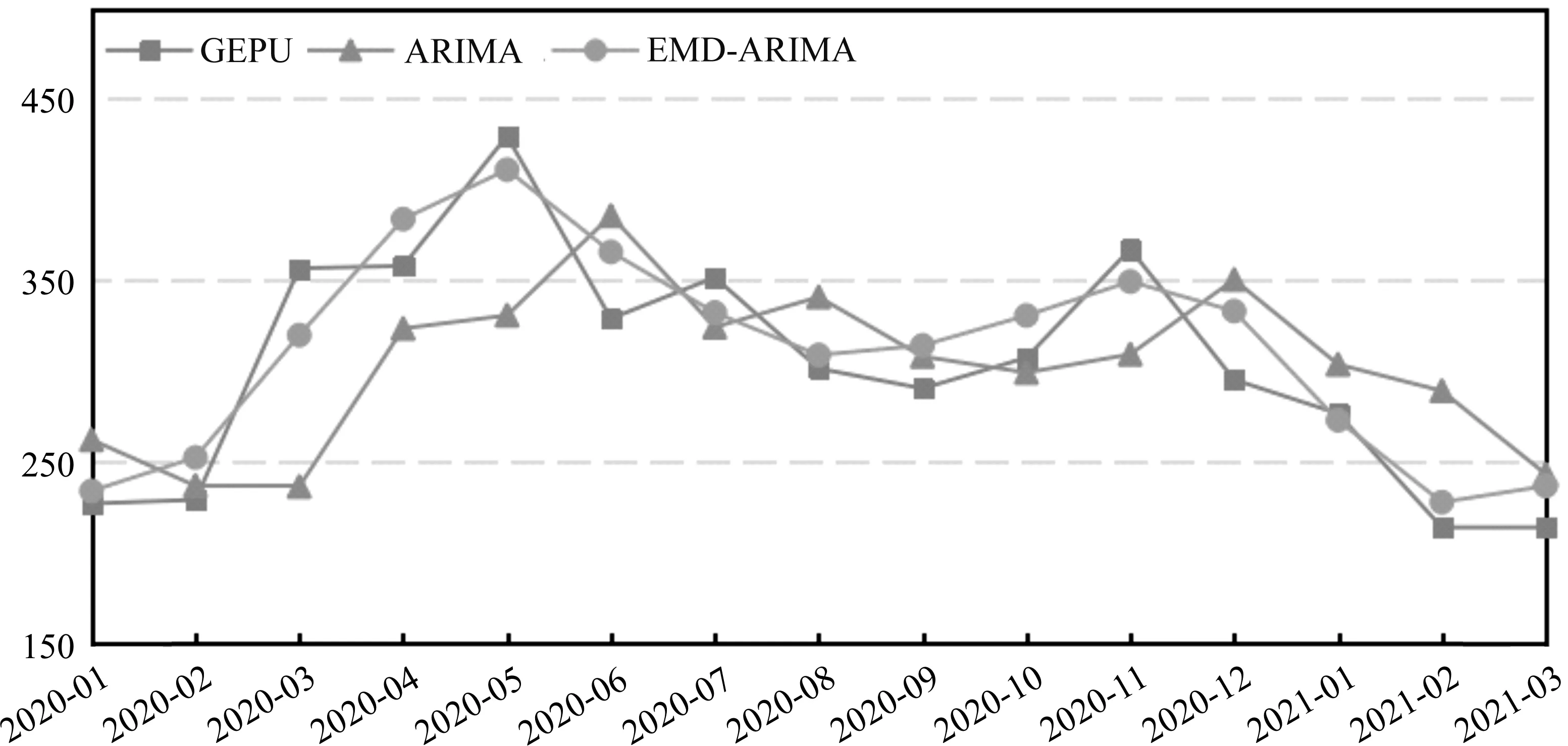
图5 两种模型对测试组的预测值与真实值的对比图

为了分析模型的可靠性，需要对模型的精度进行检验，本文采用RMSE(root mean square error)、MAE(mean absolute error)和MAPE(mean absolute percent error)三种标准对模型进行检验。公式如下：

(10)

(11)

(12)

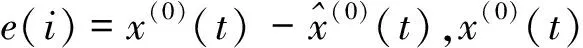
表2 ARIMA模型与EMD-ARIMA模型的预测误差

从表2中不难发现，无论对训练组数据还是测试组数据，EMD-ARIMA模型比单一的ARIMA模型预测精度都要高，其对训练组和测试组的MAPE均在10%以下。按照MAPE的精度划分级别(Lewis，1982)[57]来看，EMD-ARIMA模型的预测结果达到了高精度水平。事实上，EMD-ARIMA模型不仅能够很好地跟踪GEPU指数的趋势，而且也能较精确地拟合GEPU指数的波动。而单一的ARIMA模型只能跟踪GEPU指数的趋势，一旦数据出现较大幅度的波动，其预测误差往往会被放大，这也反映了EMD-ARIMA模型在面对复杂数据系统预测问题具有较好的稳健性和泛化能力。最后，本文对2021年4月至12月的GEPU指数做了样本外预测，预测结果如图6所示。

可以发现，2021年7月以前GEPU指数呈现上升趋势，即从264.56增加到345.90。结合当前的全球经济政治背景，本文认为该时间段的经济政策不确定性较高这一现象可能与新冠肺炎疫情存在一定的联系。从相关数据发现，全球新冠肺炎疫情确诊病例7月之前基本呈现上升趋势，由于新冠肺炎疫情全球范围的扩散，导致各个国家(地区)经济均在一定程度上受到了严重冲击。其主要原因可能如下：(1)新冠肺炎疫情提升了全球经济的不确定性。疫情的全球性暴发，致使疫情严重的国家采取一系列的限制措施导致经济停滞。全球资本市场出现了大幅度变动，一些大宗商品价格的变动超出了历史上任何时期，“黑天鹅”事件时有发生，且全球供应链出现断链的问题，导致经济出现大幅度下滑趋势。(2)新冠肺炎疫情加速了各国经济政策的不确定性。为了应对新冠肺炎疫情带来的一系列负面影响，各国政府相继制定了各种相关措施，但问题是，各国政府相关制定者只看到了措施实施带来的有利影响，却忽略了政策在实施过程中存在极大的不确定性，因为经济政策不确定性会带来国内经营环境的变化，从而会影响到国际市场参与者或国内市场参与者的预期。根据EPU的统计数据，GEPU指数近年大幅上升，由于突发公共卫生事件的影响，各国采取了积极的宏观经济政策，由于这些政策的变动非常频繁，加大了经济政策的不确定性。当然，这种由疫情带来的冲击会随着时间的推移与各国一系列相关应对政策的制定和实施力度以及新冠肺炎疫苗的全球推广而逐渐弱化，从图6可以发现，2021年7月至12月之间的经济政策不确定性相对稳定。总之，为了降低经济政策不确定性给全球贸易带来的影响，各国政府在该阶段应该加强交流与合作，避免单方面贸易保护，从而为跨国企业的发展创造和谐稳定的环境。

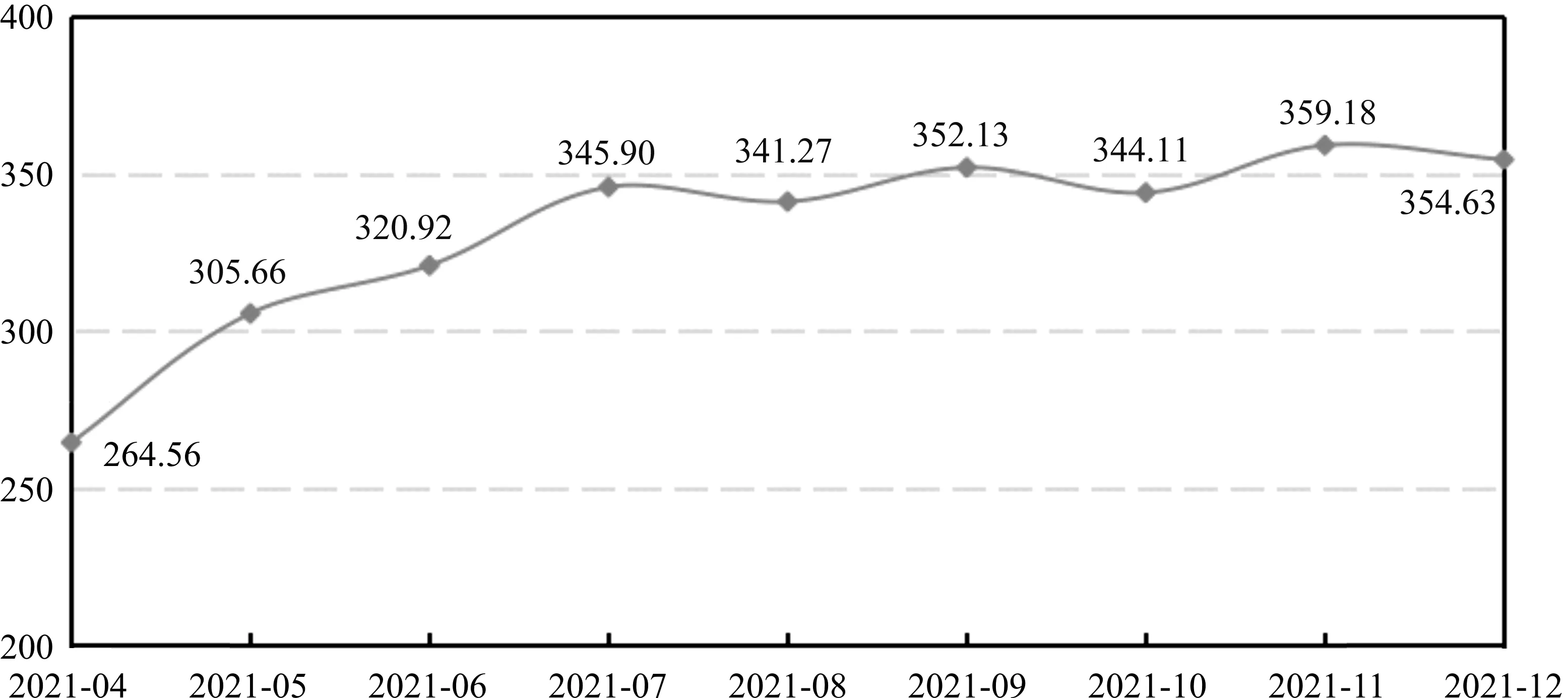
图6 2021年4月至2021年12月的GEPU指数预测值曲线

(三) 基于VAR模型的进一步分析

为了进一步考察全球贸易、新冠肺炎疫情等因素对全球经济政策不确定性的动态影响，本文采用向量自回归(VAR)模型对GEPU指数进行实证分析。该模型包括GEPU指数、全球贸易总额(TRADE)、全球新冠肺炎疫情新增确诊病例(COVID)，其中全球贸易总额(商品进口加出口)数据来源于Uncomtrade，COVID数据来源于Worldometer。为了消除季节性因素对经济变量的影响，本文应用X-12方法对GEPU指数序列以及TRADE序列进行季节调整，此外，为了缓解数据可能存在的异方差性问题，将数据进行了对数化处理。

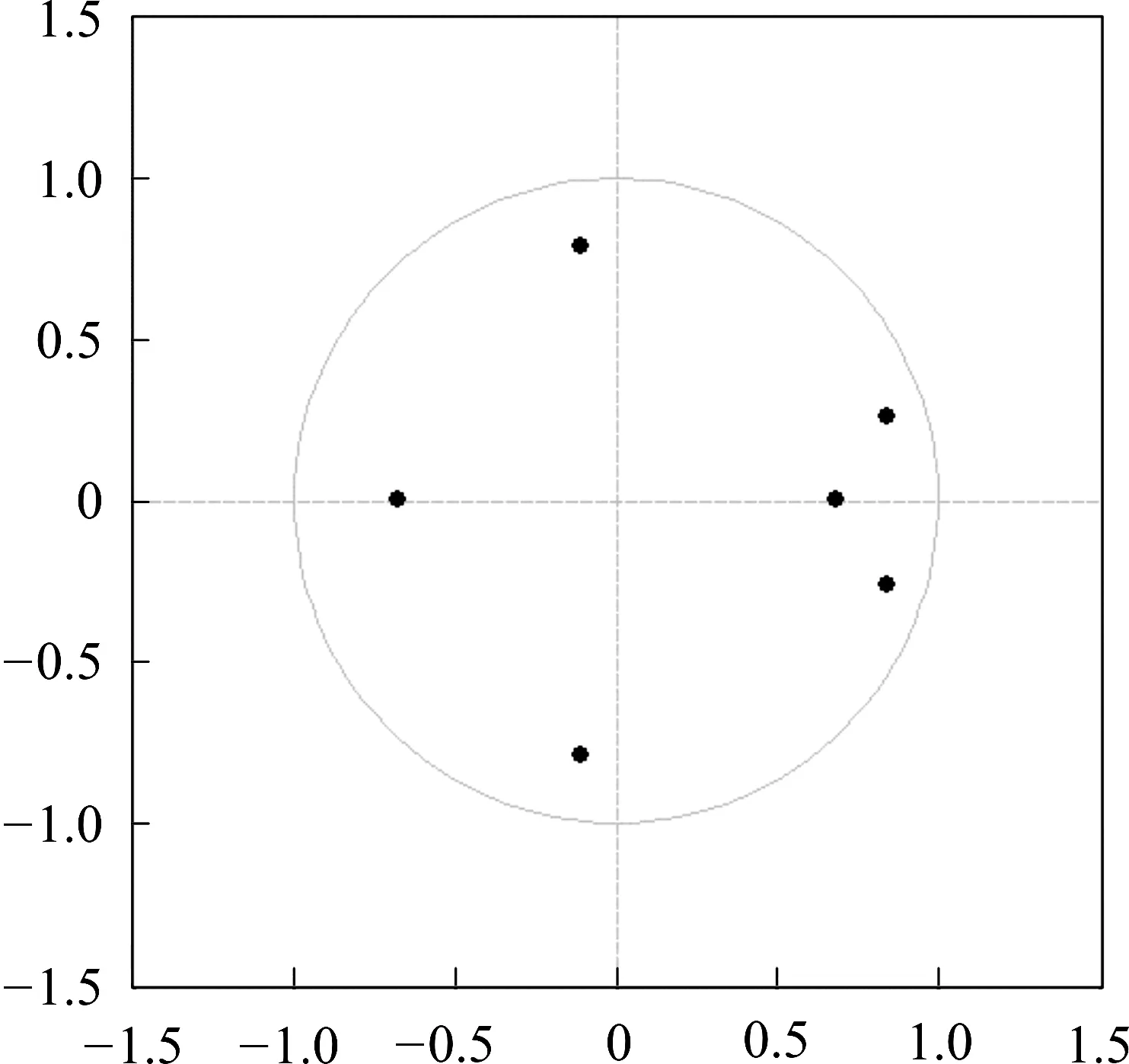
图7 VAR模型稳定性检验

首先，对处理后的数据LNGEPU_SA、LNCOVID、LNTRADE_SA进行单位根检验，由AFD检验结果发现三个变量均为一阶单整序列，调整后的变量均在p=0.05时通过显著性检验。随后，基于DLNGEPU_SA、DLNCOVID、DLNTRADE_SA三个变量一阶差分序列建立VAR模型，通过AIC、SC信息准则确定VAR模型的滞后阶数为2，建立VAR(2)模型。由于VAR模型稳定性检验是确保该模型结果有效的前提，因此，对建立的VAR模型进行AR根检验，结果发现每个AR特征根的倒数都在单位圆内，如图7所示，从而说明所建立的VAR模型是平稳的，可以进行进一步的分析。

其次，GEPU与新冠肺炎疫情和全球贸易存在一定的联系，但这种关系是否符合时间上的因果关系，则需要进一步进行格兰杰因果检验，其结果如表3所示。格兰杰因果检验显示，在5%的显著水平下，新冠肺炎疫情是全球经济政策不确定性的格兰杰原因，说明了新冠肺炎疫情的全球式暴发对GEPU存在一定的影响，但全球经济政策不确定性对新冠肺炎疫情不存在单向因果关系，即GEPU的发展对新冠肺炎疫情的影响作用有限。在10%的显著水平下，全球贸易对全球经济政策不确定性存在单向的因果关系，揭示了全球贸易的发展对GEPU存在一定的影响效果，但反之影响效果很小。

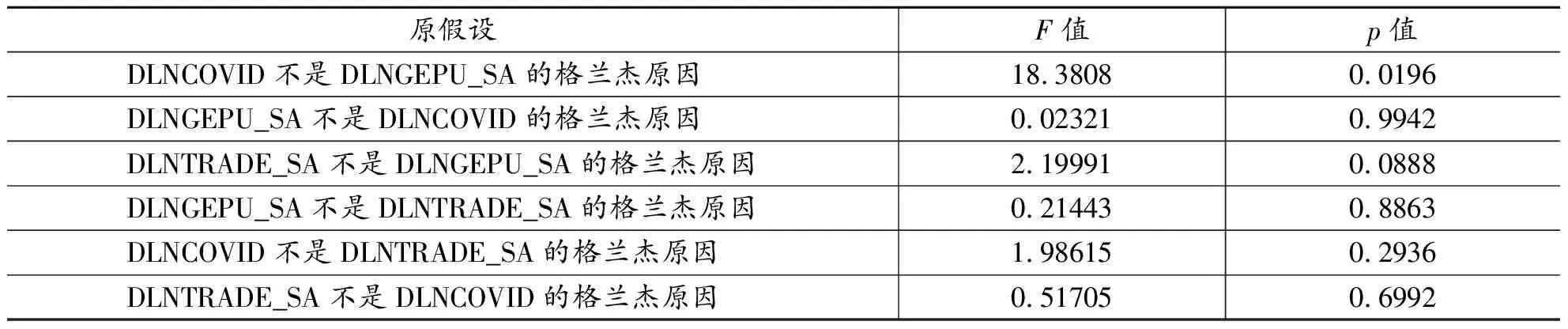
表3 格兰杰因果检验结果

再次，通过建立VAR模型，我们通过脉冲响应函数来刻画自身冲击、新冠肺炎疫情变化与全球贸易变化的冲击对GEPU的动态影响，如图8所示。DLNGEPU_SA曲线反映的是受自身冲击的脉冲响应运动轨迹，当在本期受到自身冲击后，GEPU在前期呈现快速下降的趋势，然后上升，再下降，呈现波动现象，最后响应逐渐趋于稳定。DLNCOVID曲线反映了GEPU对新冠肺炎疫情的一个标准差新息的冲击产生的脉冲响应函数图。当在本期给新冠肺炎疫情一个冲击后，在前3期存在负响应，第2期达到一个最大的负响应点，随后第4期达到一个最大的正响应点，之后下降再上升，呈现波动现象，说明新冠肺炎疫情对GEPU存在长期的影响，即新冠肺炎疫情确诊病例的增加会导致GEPU指数的上升。DLNTRADE_SA曲线反映了GEPU对全球贸易的一个标准差新息的反应图，从图中可以看到，在本期TRADE给一个正的冲击后，前2期对GEPU是一个正响应，第2期达到最大正响应，随后又变成负响应，第9期之后快速收敛。

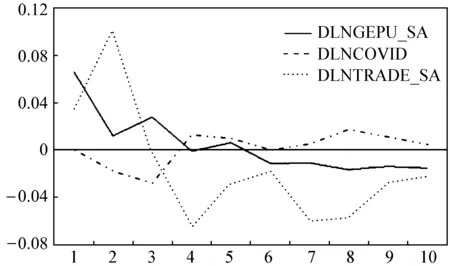
图8 各变量对GEPU冲击的脉冲响应图

最后，利用上述VAR模型对GEPU的训练组数据和测试组数据进行预测，并与EMD-ARIMA模型预测精准度对比，结果如表4所示，从而进一步说明EMD-ARIMA模型比VAR模型能够更好地预测GEPU指数的波动。

表4 VAR模型与EMD-ARIMA模型的预测误差

五、 研究结论与政策建议

(一) 研究结论

针对GEPU数据具有不确定性、非线性以及不稳定性特点，本文引入了EMD-ARIMA模型，并通过实证证明了该模型对GEPU数据有很好的适应能力。基于此模型，本文得到了如下结论：(1)作为主流的非平稳时间序列预测模型，ARIMA模型能够有效拟合GEPU指数的总体变化趋势，但是预测误差偏高，对测试组和训练组的平均相对百分比误差分别高达12.74%和15.06%。(2)与ARIMA模型相比，EMD-ARIMA模型能有效地解决由原始数据不确定性、非线性以及不稳定性所导致预测偏差问题，得到精度较高的预测结果，其预测误差分别为8.76%和7.10%。(3)通过利用平稳数据构建VAR模型，进一步地构造脉冲响应函数进行分析，发现新冠肺炎疫情以及全球贸易的变化对GEPU存在一定的影响。(4)基于EMD-ARIMA模型，本文发现在2021年7月之前GEPU指数呈现出增加的趋势。(5)由新冠肺炎疫情带来的冲击随着时间的推移与相关应对政策的出台以及新冠肺炎疫苗的全球式推广而逐渐弱化，经济政策不确定性会在2021年7月至12月之间趋于稳定。

(二) 政策建议

由本文样本外预测结果可知，2021年7月至12月间基本趋于稳定，当前受到新冠肺炎疫情的影响，应该充分认识到全球经济政策不确定性对国际贸易存在的负面影响。首先，各国监管当局应当在经济全球化的视域下建立和完善面向经济政策不确定性的监测、评估和预警机制，建立健全风险防控体系。与此同时，相关部门应加强完善信息披露制度，引导各类经济主体根据实际情况作出合理预期，防范国际事件的急剧上升对本国经济造成不利的影响。

其次，各国要提高应对全球经济政策不确定的针对性和精准性，主动寻求应对方法，化解全球经济政策不确定性对本国经济发展带来的不利影响。一方面要增强本国经济政策的稳定性和连续性,为经济主体提供稳定的政策环境,进一步地增强对国际事件冲击的吸收能力;另一方面也要紧密关注其他国家特别是贸易往来密切国家的经济运行状况,并能够及时根据相关国家发生的一些国际事件采取有效的措施。

最后，各国政府要进一步地加强国家之间信息交流和政策沟通，建立宏观经济政策协调机制，增强政治互信，避免单方面贸易保护和政策冲突，有效预防和规避各国经济政策波动带来的不确定性，为促进企业跨国贸易和投资创造和谐稳定的环境。