基于误差建模分析的深度神经网络大蒜价格预测应用

山东农业大学信息科学与工程学院 王俊美 张超 刘震

大蒜作为一种调味品，属于小宗农产品，产量相对较少，产地集中，每年的大蒜产量上下浮动空间大，而需求弹性不足，这种特殊的供求关系也让大蒜吸引不少社会游资进行炒作，对价格走势推波助澜。2009 年“炒蒜潮”中，全国大蒜半年上涨40 多倍，很多中间商获得巨额利润。“蒜你狠”一词，也广为消费者知晓。在投机者看来，蒜市犹如赌场。赌对了可一夜暴富，开豪车衣锦还乡；赌错了则债台高筑，因此各路投机者通过多种手段影响价格。

近些年，大蒜价格的“过山车”状况频现，一方面反映出当前农产品市场的信息不对称，一点儿风吹草动都可能带来行情的巨大波动；同时表明由于大蒜市场总体体量小，价格很容易遭到炒作。

研究近年来我国大蒜市场价格的运行轨迹，大蒜市场一直没有走出暴涨暴跌的怪圈。大蒜作为一季生产、常年消费的农产品，价格涨涨跌跌、宽幅震荡，有其商品属性造成的客观性。

大蒜市场价格的稳定，根本上取决于供求关系基本平衡，而供求关系的基本平衡，要求市场需求、种植面积和单位产量三个方面同时基本稳定或同步相向变化。由于我国农产规模化程度低，基础薄弱，要做到这三者基本稳定或同步相向变化，难度非常大。市场信息的不全面和混乱，让蒜农在决定种植的时候，没有能力了解国际市场和国内市场的供求关系，只能根据上一年的盈亏与否或跟风种植。经销商不能准确掌握全国的种植面积、产量和库存，只能凭经验、靠感觉，价格上涨就跟风收购、价格下跌就争相出逃，客观上放大了供求关系的不平衡，加剧了价格涨跌的幅度和速度。

因此为了解决大蒜价格的预测问题，很多研究人员利用不同的算法来进行价格预测，提高准确率，本文在总结前人的方法的基础上进行了各种方法比较。

想要研究并分析一个事物的原理时，通常的办法就是通过观察事物并对其建立一个数学模型。众所周知，模型永远不是完美的，总会出现这样或那样不可免的误差。要想研究大蒜价格的未来趋势，就要先对大蒜的价格建立一个合适的数学模型（例如时间序列模型），但模型总会与原来的观测值有差别，即误差。对建模产生的误差进行分析就是本文所要解决的问题。

人们总希望计算机能够帮助我们处理各种各样人类所不能解决的或者对于人类来说过于繁琐的问题。从简单的计算数据，到后来的手机语音助手、摄像头图像识别、手机等语音识别等。人们总希望计算机可以越来越智能，在这种情形下，科学家依照人脑建立了人工神经网络。这就是本文主要用到的方法：神经网络。由于深度神经网络具有许多优良的特性，其在建模分析中发挥巨大的作用。

在本文中先对大蒜的观测值建立时间序列模型，得到建模所产生的误差。然后利用深度神经网络研究并分析产生的误差，以此来预测误差未来的走势。

1 数据来源与预处理

本文数据来源于国际大蒜贸易网所提供的大蒜——周批发价格指数。时间从2013 年1 月4 日至2018 年1 月26 日共252 周数据。数据透视表如下:

时间 定基指数Length:252 Min. 213 Class 1st 286.4 Median 408 Mean 466.9 3rd 520.1 Max. 1103.9

2 研究方法与思路

为解决预测问题，本文将利用三种算法进行比较，使用传统的ARIMA 进行建模分析，其次使用循环神经网络进行预测，最后使用组合模型进行分析，并利用RMSE 进行精度分析。

2.1ARIMA 模型分析

首先选用ARIMA 模型对时间序列数据建立时间序列模型，对大蒜的周价格进行建模以及分析。

图1 大蒜周价格原始数据图

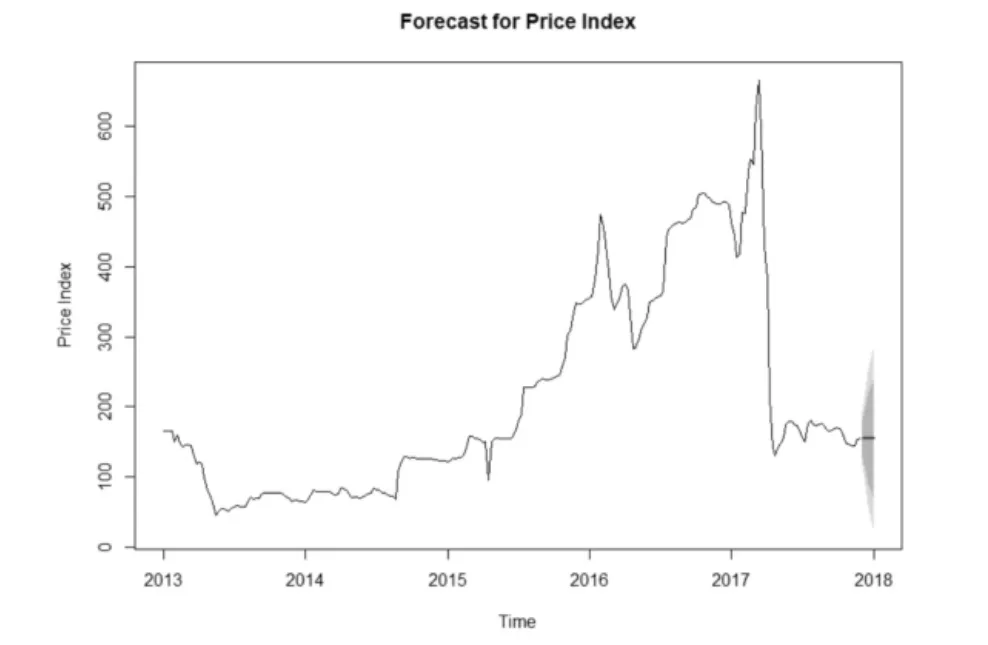
图2 ARIMA 大蒜周价格预测图

2.2 神经网路分析

其次使用神经网络进行建模分析，在利用神经网络对时间序列预测之前，首先要先建立神经网络。

而对于建立神经网络最为重要的问题就是如何确定输入层和输出层节点个数以及隐含层层数和每层节点个数。隐含层的层数以及节点数应根据数据量以及数据类型来确定，过多的隐含层或者节点极容易造成过拟合问题。输入层以及输出层的节点则根据需要输入以及输出的数据来确定。

迭代方式为将隐含层的节点固定在区间[30,80]（最少的节点数约等于数据数量，最多的节点数约等于数据的二倍）内，迭代步长为10。检测方式为先选取大蒜价格的前90%的数据作为训练数据data train 来训练神经网络，而大蒜价格的后10%的数据作为测试数据data test 来测试神经网络。即当神经网络训练完成以后，用该神经网络去预测后面的测试数据。将预测数据与实际观测值比较得到均方差RMSE，以均方差为标准选择合适的节点数。由于神经网络权值的更新具有随机性，所以对于不同节点数的神经网络进行三次独立的检测，取得三次RMSE 的平均值，以此来减少误差。经过迭代得到：当节点数分别为 30，40，50，60，70，80时用神经网络预测后百分之十（测试数据）得到的均方差分别是：239.8324,219.6529,206.3730,219.8147,190.17 44,186.1080。

可以发现当节点数为80 的时候，均方差最低。但从数据上来看，随着节点数量的增加均方差就越少。所以有可能当节点数更高时，均方差可能会越少。实际上确实是这样，当节点数为 90，100 时均方差为183.2896，176.7150。但由于训练数据较少，太多的节点数容易造成过拟合，所以不予考虑90 以及更多的节点数。所以就将节点数确定为80。节点为80 时，实验的结果如下：

图3 就是用LSTM模型对原始数据进行五个周预测的结果。

图3 神经网络残差分析对比图

接着用上面的方式对建模产生的误差进行预测。首先建立LSTM，用前90%的数据作为数据训练，然后测试后10%的数据。经过迭代得到：当节点数为200，220，240，260，280，300 时用神经网络预测后百分之十（测试数据）得到的均方差为9.9943，13.2003，9.7888，9.0660，9.2775，9.8848。从数据中看当节点数为 260 时，均方差最小。而且对周价格直接预测时节点数也是260，则将节点数确定为260。

从图中看对最后10%的预测与实际观测值相差不大。则认为该LSTM神经网络建立成功。下面将所有数据用于训练，以及进行后五个周误差预测，预测数据为：6.2618，-18.0115，4.4335，-12.7263，21.3424 如下图所示。

图4 神经网络预测图

2.3 组合模型分析

最 后 将 用 ARIMA 预 测 ，LSTM 预 测 以 及LSTM&ARIMA 预测放在一起比较。如下图所示。

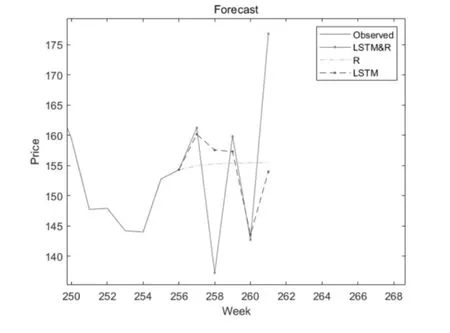
图5 三种模型预测对比图

其中红色表示直接用ARIMA 预测；绿色表示直接用LSTM预测；蓝色表示两者一起预测。从上图看直接用ARIMA 预测得到的数据较为平稳，两者结合预测得到的数据图像波动较大，直接用LSTM预测得到的数据图像波动较介于两者中间。两者结合预测得到的数据更贴合前面的数据，最终认为LSTM 神经网络加ARIMA 的预测相对较好。

3 结论

综上,单纯使用ARIMA 模型进行预测与单纯使用神经网络进行预测其误差都比较大，但是当预测方法或者预测次数增加时，预测出来的值或许与真值越贴合。但具体增加多少次，用几种预测方式，属于另一个问题，也可以在以后改进模型的时候再加以分析。