一类连续预防接种的母婴传染病模型的稳定性分析
2022-04-21王俊荣
王俊荣
(山西应用科技学院 山西太原 030000)
母婴传染病一直是人类关注的话题之一,它给许多家庭带来了不幸和灾难.近年来,随着生活水平的提高,环境受到严重的破坏,这对优生有着很大的影响.目前有大量研究母婴传染病规律的文献[1],且在研究过程中考虑的与传染有关的因素也越来越全面,使研究得到的结论更符合了实际的需要.文献[1]建立了SIR模型,讨论标准传染率、垂直传染和连续预防接种对传染病的影响,并且得出避免传染病发展成地方病的措施.文献[2]讨论了标准形式接触率的SIRS模型的定性分析,并分别研究了连续方式和不连续方式的控制策略,丰富了传染病动力学的研究工作.文献[3-4]介绍的是关于SEIR传染病模型的稳定性分析.文献[5]讨论了人口数是非常数的SEIS传染病模型的全局稳定性.文献[7]讨论的是两类传染病模型关于预防接种的稳定性分析.文献[7-10]详细地介绍了传染病的相关理论知识.
通过阅读大量关于母婴传染病模型的文献,文章讨论在双线性传染率下,连续预防接种的母婴传染病SIRS模型的动力学行为.最后得出人口输入率、自然死亡率、因病死亡率、母婴传染率、病人恢复能力、抗体有效率和预防接种率等对传染病模型的动力学行为都有影响,并且它们之间也相互影响.
1模型建立
根据具有连续预防接种的母婴传染病的传染机制图,作如下假设及符号说明,见图1.
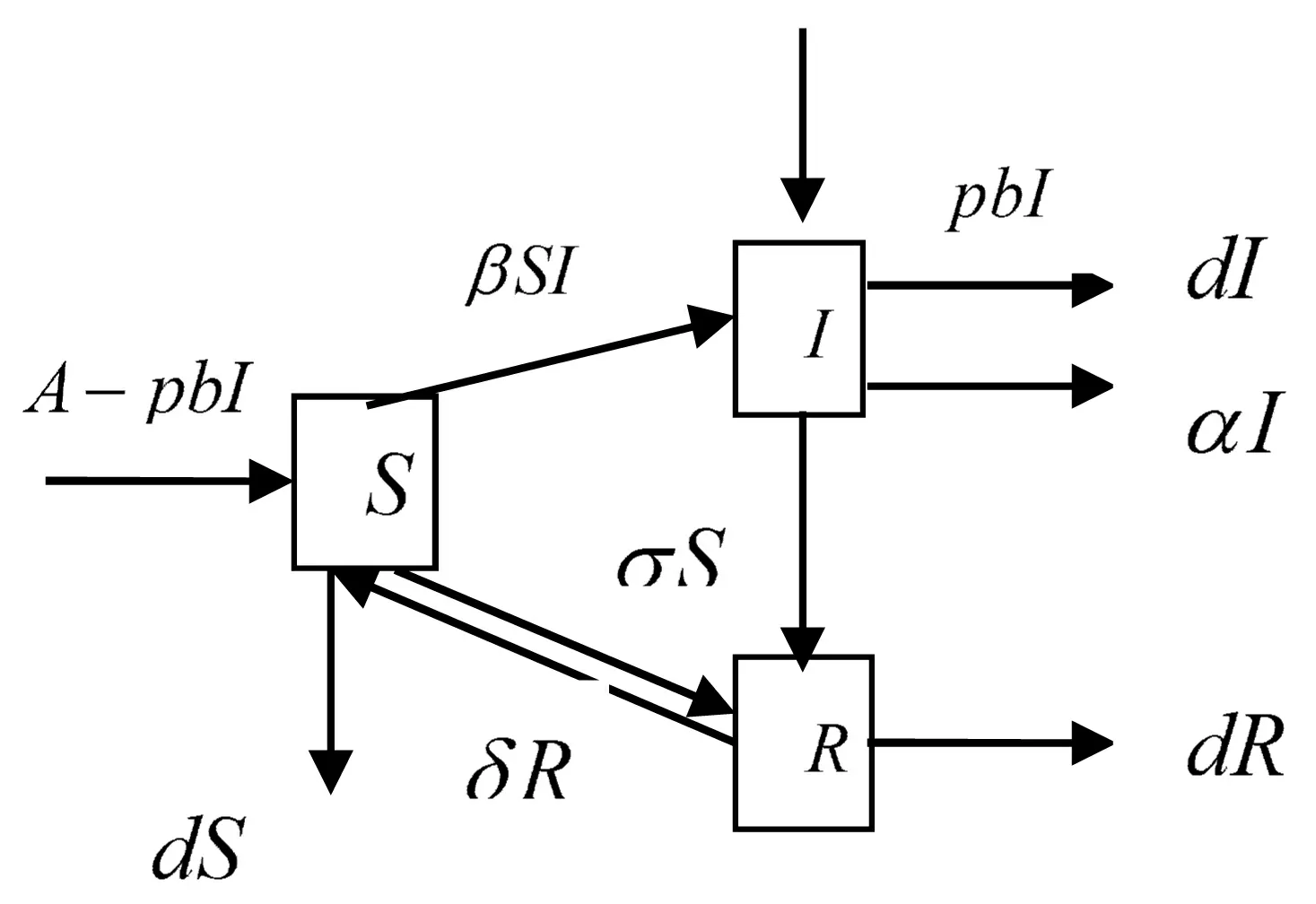
图1 疾病的传染机制图
(1)S、I、R分别表示易感者、疾病者、移出者;
(2)人口总数为N,N=S+I+R;
(3)S中未被预防接种的、R中抗体失效的和I中新生儿没有被垂直感染的部分都是易感者;
(4)A新生儿常数输入率,b新生儿出生率,d自然死亡率,α因病死亡率,p垂直传染率,ε恢复率,δ抗体失效率,σ预防接种比例,β一个病人能感染易感染者生病的比例.
模型为:
(1)
2平衡点的存在性
定理1 结合系统(1)的实际意义, 系统(1)的一个正向不变集是
证明:由系统(1)可知,总人口方程
解得:
则有:
又因S、I、R都是非负数,故定义:
则D是系统(1)的一个正向不变集.
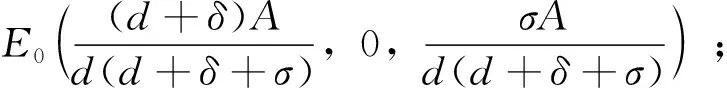
证明:(1)当I=0时,(1)就等价于:
(1)
系统(1)的平衡点满足:
则解得:
即存在无病平衡点

故当ε+d+α>pb时,S>0,记为S+.
将S的值代入(1)中,得:
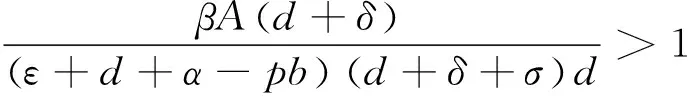
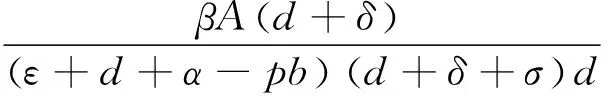
3平衡点的稳定性分析
定理3 当R0≤1时,系统(1)的无病平衡点E0全局渐近稳定,且平衡点E0是结点;当R0>1时,E0不稳定,此时平衡点E0是鞍点.
证明:系统(1)在

该Jacobi矩阵的特征值满足方程:
(λ+H1)(λ+H2)(λ+H3)=0
对应的特征值有:
因此,由文献[11]定理3.11可知,当R0≤1则有H3≤0,则系统(1)的无病平衡点E0是局部渐近稳定的,又因三个特征值λ是互不相等且同号的实数,故平衡点E0是结点;若R0>1则有H3>0,则E0不稳定,又因特征值λ是异号实数,故平衡点E0是鞍点.
下面证明R0≤1时,系统(1)的无病平衡点E0全局渐近稳定.
构造Liapunov函数,令:
V(t)=I(t),
沿系统(1)轨线的导数为:
=[βS+pb-(ε+d+α)]I
=(R0-1)(ε+d+α-pb)I
≤0
所以,当I(t)→0,R(t)→0(t→∞)时,系统(1)的极限方程:
得:

由上述证明可知,当p=0或σ=0时,结论仍成立.
定理4 当R0>1时,系统(1)的地方病平衡点E+局部渐近稳定.
证明:系统(1)在E+(S+,I+,R+)处的Jacobi矩阵为
该Jacobi矩阵的特征值满足方程:
λ3+A1λ2+A2λ+A3=0
其中:
A1=βI++2d+σ+δ>0,
A2=βI+(2d+ε+σ+δ)+d(d+σ+δ)>0,
A3=βI+[εd+(d+α)(d+δ)]>0,
A1A2-A3=βI+d(2βI++4d+σ+δ)+d2(2d+σ+δ)+βI+ε(βI++d+σ+δ)+βI+α(βI++2d+σ)+αδ+(βI++2d+σ+δ)(βI+δ+dδ+σd)>0
因此由Hurwitz判据可知,系统(1)地方疾病平衡点E+(S+,I+,R+)是局部渐近稳定的.
若p=0或σ=0时,由上述证明知,结论仍成立.
4数值模拟
下面用MATLAB进行数值模拟,进一步验证定理3和定理4的可靠性.
(1)取A=0.4,β=0.2,d=0.3,δ=0.3,ε=0.5,α=0.1,b=0.2,σ=0.3,由定理2可知,只要p≤1就能满足无病平衡点E0全局渐近稳定,即疾病被根除.取一组初值S(0)=1,I(0)=0.375,R(0)=0.225,对不同的p进行模拟,结果如图2.其中,图(a)、图 (b)和图(c)分别表示母婴传染率是0、0.5、1的情形下易感染者、染病者和恢复者人数的变化趋势.

(a) (b)

(c)图2 R0≤1时,在不同p值下S、I、R随时间t的变化趋势
从图2可以看出,当R0≤1时,疾病被根除,同时易感染者和恢复者人数都趋于稳定状态,则定理3得到验证.同时,也发现当R0≤1时,母婴传染率对易感染者、疾病者和恢复者人数变化的影响不明显.
(2)取A=0.4,β=0.2,d=0.3,δ=0.3,ε=0.5,α=0.1,b=0.2,p=0.5,由定理2可知,只要σ≥0就能满足无病平衡点E0全局渐近稳定,即疾病被根除.取一组初值S(0)=1,I(0)=0.375,R(0)=0.225,对不同的σ进行模拟,结果如图3.其中,图(d)、图 (e)和图(f)分别表示预防接种率是0和0.5的情形下易感染者、染病者和恢复者人数的变化趋势.

(d) (e)

(f)图3 R0≤1时,在不同σ值下S、I、R随时间t的变化趋势

(3)当其余值不变,取p=0.5,σ=0.5时,初值仍为S(0)=1,I(0)=0.375,R(0)=0.225,观察S、I、R随时间t的变化趋势,结果如图4所示.

图4 R0≤1时,在p=0.5,σ=0.5的值下S、I、R随时间t的变化趋势
通过观察图4,发现无病平衡点E0的类型是结点,符合定理3.
(4)取A=0.6,β=0.7,d=0.3,δ=0.3,ε=0.2,α=0.1,b=0.2,σ=0.3,由定理3知,需p>0.13就能满足地方病平衡点E+局部渐近稳定,即疾病发展成地方病.取一组初值S(0)=1,I(0)=0.375,R(0)=0.225,对不同的p进行模拟,结果如图5.其中,图(a)、图 (b)和图(c)分别表示母婴传染率是0.2和0.7情形下易感染者、染病者和恢复者人数的变化趋势.

(a)
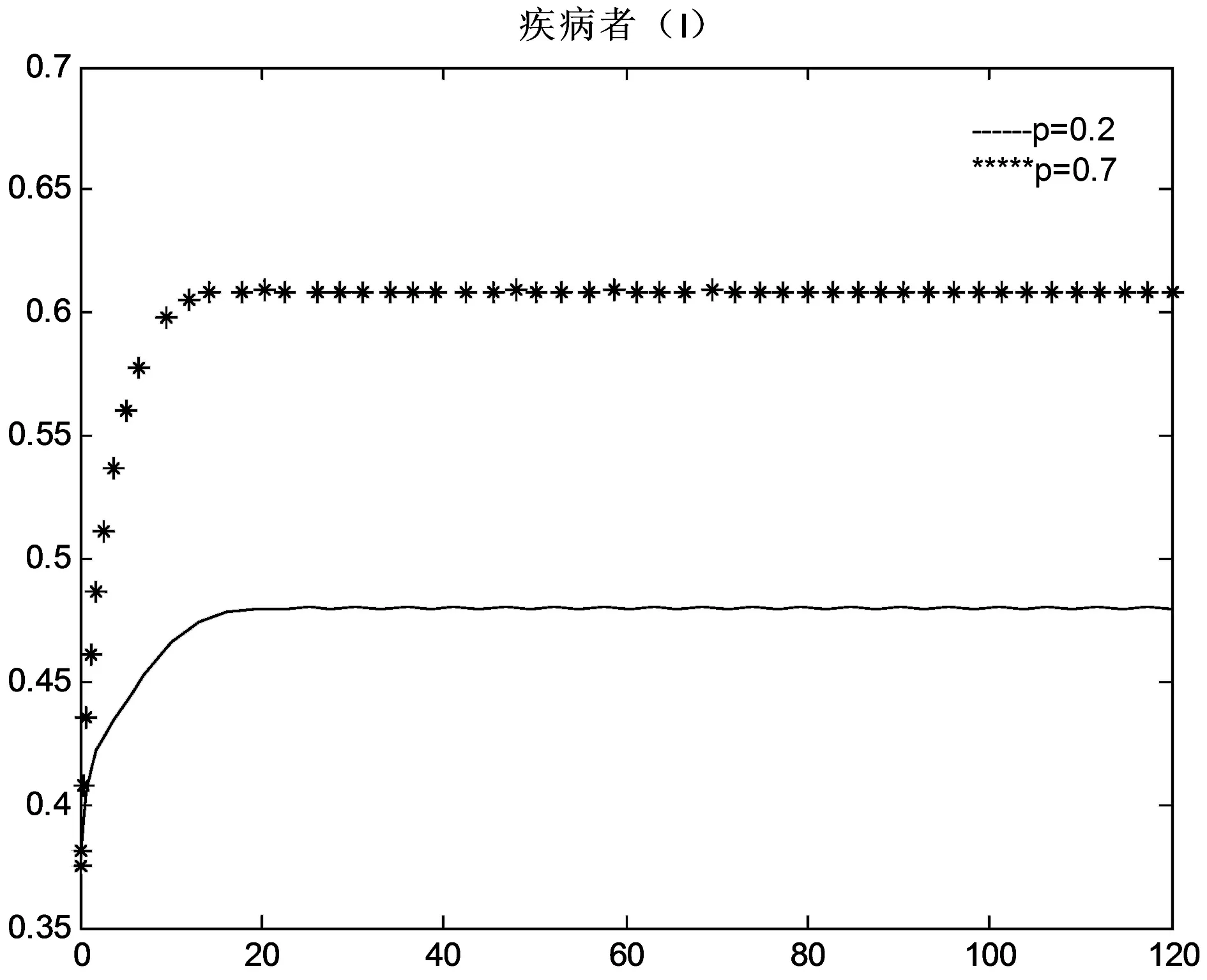
(b)

(c)图5 R0>1时,在不同p值下S、I、R随时间t的变化趋势
从图5可以看出,当R0>1时,疾病将发展成地方病,同时易感染者和恢复者人数也都趋于稳定状态,则定理3得到验证.但是观察图(a)、(b)和(c),发现降低母婴传染率可减少疾病人数.因此,为防止疾病发展成地方病或者减少疾病人数,应努力降低母婴传染率.
因母婴传染不仅仅可以通过胎盘感染婴儿,还可以通过产道和母乳感染婴儿,所以如果携带可遗传病毒的妊娠女性,应停止妊娠进行药物阻断或者进行人工喂养婴儿,有效降低母婴传染率.
(5)取A=0.6,β=0.7,d=0.3,δ=0.3,ε=0.2,α=0.1,b=0.2,p=0.7,由定理3知,需σ<1就能满足地方病平衡点E+局部渐近稳定,即疾病发展成地方病.取一组初值S(0)=1,I(0)=0.375,R(0)=0.225,对不同的σ进行模拟,结果如图6.其中,图(d)、图 (e)和图(f)分别表示预防接种率是0和0.7情形下易感染者、染病者和恢复者人数的变化趋势.

(d) (e)
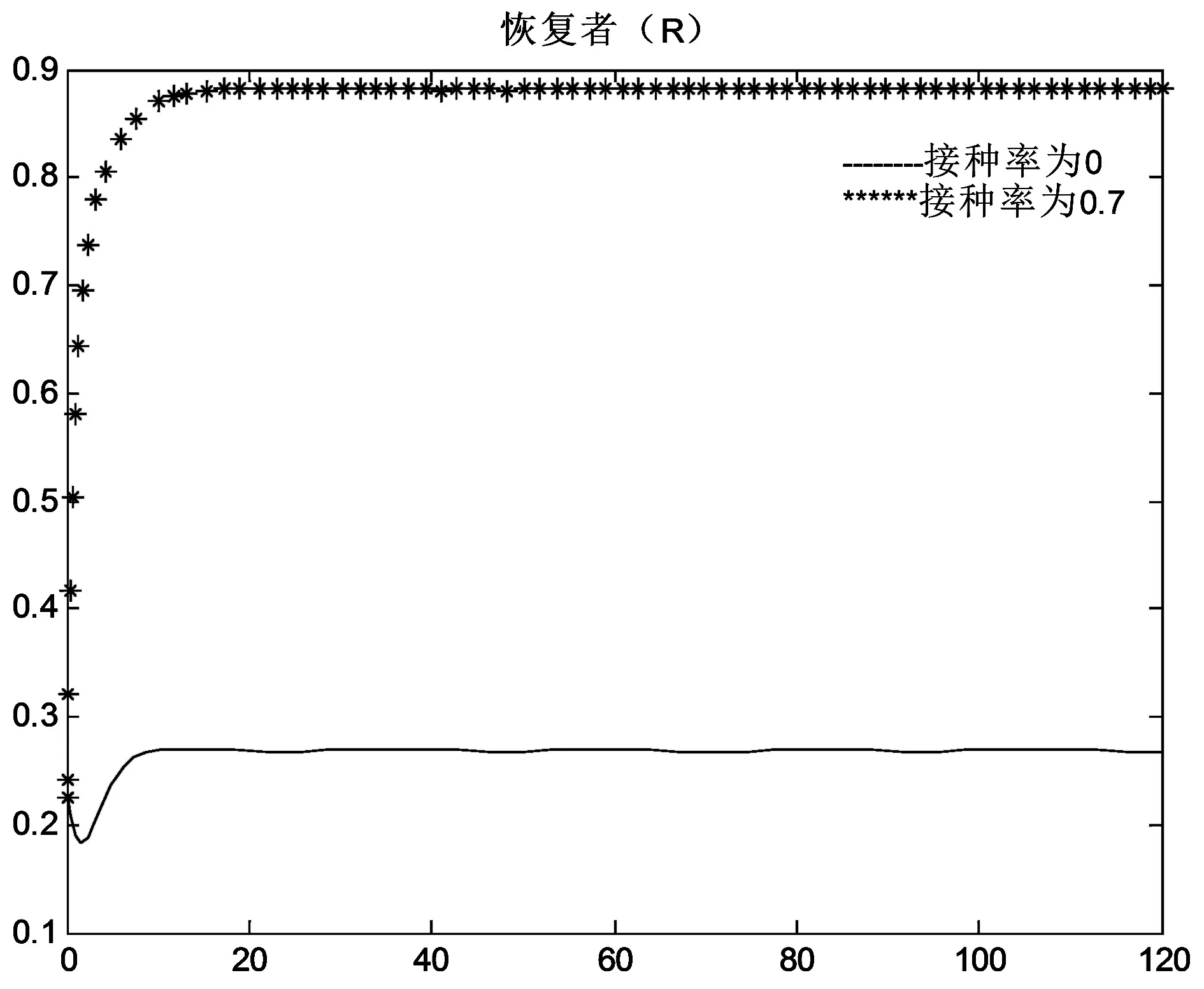
(f)图6 R0>1时,在不同σ值下S、I、R随时间t的变化趋势
从图6可以看出,当R0>1时,疾病将发展成地方病,同时易感染者和恢复者人数也都趋于稳定状态,则定理4得到验证.但是观察图(e)和(f),发现增加接种率可减少疾病人数.因此,为防止疾病发展成地方病或者减少疾病人数,应努力增加抗体接种率.
(6)取A=0.6,β=0.7,d=0.3,δ=0.3,ε=0.2,α=0.1,b=0.2,p=0.7,σ=0.3.初值仍为S(0)=1,I(0)=0.375,R(0)=0.225,观察S、I、R随时间t的变化趋势,结果如图7所示.
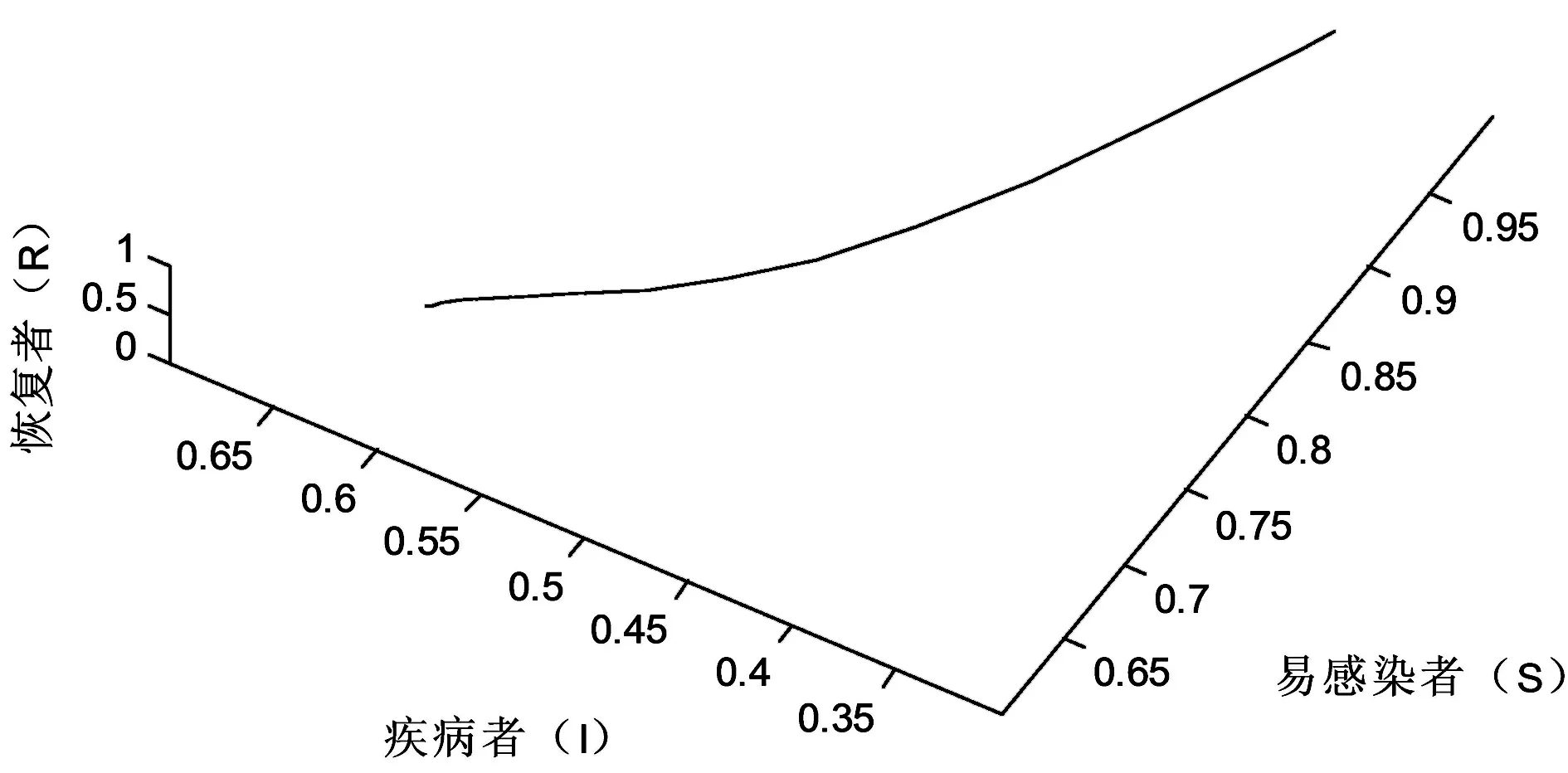
图7 R0≤1时,在p=0.7,σ=0.3的值下S、I、R随时间t的变化趋势
通过观察图7,发现无病平衡点E0是鞍点,符合定理2.
5结论
(1)文章主要研究了母婴传染和连续预防接种对双线性发病率的SIRS传染病的衍化趋势进行了定性分析。文中通过对基本再生数R0的讨论,得出:当R0≤1时,无病平衡点全局渐近稳定,此时疾病将被根除;当R0>1时,无病平衡点不稳定,地方病平衡点局部渐近稳定,疾病将会持续存在.
(2)当R0≤1时,预防接种率的高低对易感染者和恢复者的人数有很大影响,但母婴传染率对易感染者、疾病者和恢复者的人数变化影响不明显.
当R0>1时,预防接种率和母婴传染率的高低对疾病者的人数有很大影响,故防止疾病发展成地方病或者减少疾病人数,应努力增加预防接种率和降低母婴传染率.
(3)关于有效降低母婴传染率的具体措施有进行药物阻断、剖腹生产和人工喂养婴儿.
(4)人口输入率、自然死亡率、因病死亡率、母婴传染率、病人恢复能力、抗体有效率、预防接种率和有效接触率对传染病都有一定的影响,而且它们之间也相互制约和相互影响.
(5)文章通过对母婴传染病SIRS模型的研究,为该类传染病的防治提供了理论依据和数量依据.文章在传染病模型中主要考虑的是连续预防接种,对于不连续预防接种状态下的母婴传染病也在研究中.
