直升机吊挂钝体吊挂物建模及前飞稳定性研究

苏小恒

（中国直升机设计研究所 飞行控制部，江西景德镇，333001）

外吊挂运输是直升机的典型任务之一，应用领域十分广泛。但由于吊挂载荷的多样性，使得直升机吊挂运输适航取证过程充满挑战，研究表明经过验证的仿真模型能够显著降低吊挂适航取证的风险和成本[1]，其中在悬停小速度或针对特定吊挂物时吊挂仿真模型已取得足够准确的结果。在吊挂适航取证中，当前吊挂构型的前飞速度限制是编制飞行手册的重要依据，吊挂集装箱飞行试验得到的速度包线远小于基于准定常气动载荷吊挂模型的仿真结果。吊挂集装箱的飞行速度限制是由于吊挂物的摆动不可接受，仅使用准定常气动载荷无法预测吊挂物的不稳定性，吊挂物的不稳定性是由其非定常气动载荷导致的[2]。因此基于非定常气动载荷建立钝体吊挂物仿真模型，研究其在前飞时的稳定性对吊挂适航取证具有重要意义。

国内相关研究的吊挂物气动建模大多基于准定常气动载荷[3]，国外针对吊挂物非定常气动载荷以CFD仿真和试飞试验开展了大量研究。da Silva[4]等对CFD仿真数据进行参数辨识，建立了非定常偏航力矩系数和侧向力系数对侧滑角的1阶传递函数模型，并对侧向力系数的传递函数模型进行了验证；Cicolani[2]等根据风洞试验数据和试飞实测数据进行参数辨识，建立了非定常偏航力矩系数对准定常偏航力矩系数的5阶传递函数模型。

本文针对试飞中多条吊索的物理连接状态建立了多级吊索系统模型和旋转接头模型，根据风洞试验数据和试飞实测数据[5]建立了钝体吊挂物集装箱的非定常气动力和力矩的传递函数模型，结合直升机非线性飞行力学模型，针对几种典型吊挂状态研究了直升机吊挂钝体吊挂物的前飞稳定性。

1 直升机吊挂系统建模

本文所建立的直升机吊挂系统包括：由5根吊索组成的多级吊索系统、主吊索与分吊索之间的旋转接头和钝体吊挂物集装箱。如图1所示，其中节点1到2之间为主吊索，节点2到3、2到4、2到5和2到6之间分别为4根分吊索。

1.1 单根吊索建模

吊索建模考虑了其质量特性、刚度特性和阻尼特性，气动特性较小可忽略，将吊索简化为由多段长度相同的质量-弹簧-阻尼单元相连接组成的系统，如图1所示。

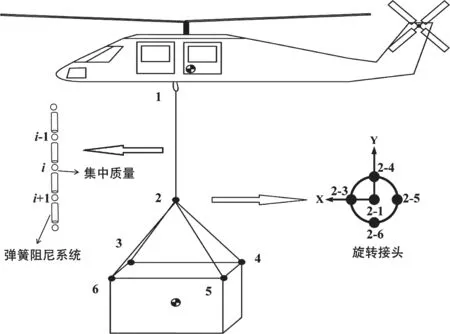
图1 直升机吊挂系统

设节点i-1、i、i+1处的位置矢量分别为，则第i-1和第i个弹簧在节点i处弹簧拉力的方向矢量分别为，单位方向矢量分别为弹簧伸缩速率分别为，第i-1和第i个弹簧的弹簧拉力分别为：

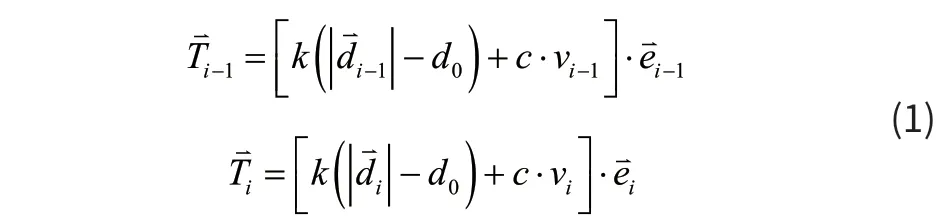
其中k为弹簧刚度系数，c为弹簧阻尼系数，d0为每个吊索分段的初始长度。

第i个集中质量的动力学方程为：

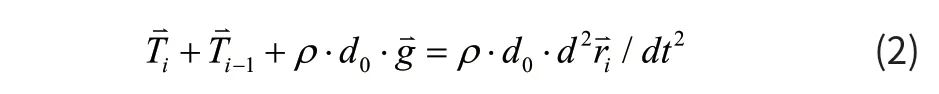
其中ρ为吊索的线密度。

1.2 多级吊索和旋转接头建模

主吊索和4根分吊索之间用旋转接头连接，如图1所示。旋转接头的坐标系定义为：原点为节点2-1，x轴向前，y轴向右，z轴向下。旋转接头具有3个移动自由度和绕z轴的转动自由度（带有旋转刚度和旋转阻尼），由旋转接头传递给主吊索的扭转力矩远小于主吊索拉力对直升机重心产生的力矩，可忽略。

旋转接头上的节点2-1连接主吊索，节点2-3、2-4、2-5和2-6分别连接4根分吊索。主吊索在节点2-1处的集中质量为 1m，4根分吊索在旋转接头上对应节点处的集中质量均为 2m。旋转接头的半径为l，质量为m，将旋转接头的质量均匀集中至节点2-3、2-4、2-5和2-6处。设旋转接头上节点2-1的加速度矢量为，则集中质量点2-3、2-4、2-5、2-6和2-1的动力学方程分别为：

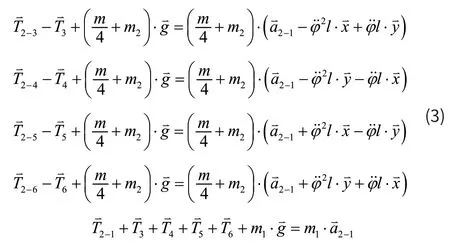
其中φ为旋转接头旋转的角度，为坐标轴的单位方向矢量，为吊索对旋转接头上连接点的吊索拉力，为旋转接头对各连接节点处集中质量的约束力。

分吊索拉力对旋转接头节点2-1处的力矩在z轴的分量应与旋转接头绕z轴转动产生的扭转力矩相抵消，即：

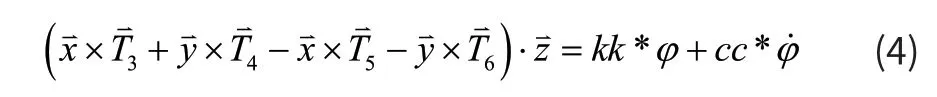
其中kk为旋转刚度，cc为旋转阻尼。

1.3 吊挂物建模

吊挂物模型由气动载荷模型和6自由度刚体动力学模型组成。

（1）气动载荷模型

由风洞试验数据可以得到吊挂物风轴系下的准定常气动力系数：

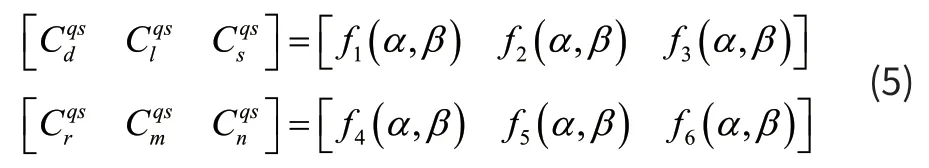
其中α、β为吊挂物迎角和侧滑角，通过转换矩阵将风轴系气动系数转换成体轴系（原点为吊挂物几何中心，x轴向前，y轴向右，z轴向下）气动系数

钝体吊挂物的流场环境复杂，很难在仿真中建立精确的非定常气动模型，目前还没有有效的方法能够直接获取钝体吊挂物的非定常气动特性。在图1所示的吊挂构型下，钝体吊挂物的航向是不稳定的，在试飞中往往处于旋转状态。旋转钝体吊挂物的气动载荷通常包括：定常气动力、角速率引起的黏性阻尼和由于气流分离、尾涡增大和脱落时相位滞后引起的非定常气动力[4]。文献[4]中以二阶传递函数形式计算非定常气动力，建立的传递函数模型为：

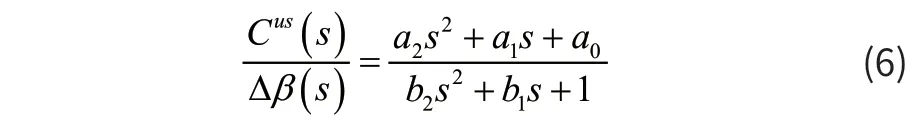
其中Cus为非定常气动力系数。通过对CONEX集装箱不同侧滑角下的非定常气动力系数进行扫频辨识研究，对于偏航力矩系数，式(6)中参数a2=b2= 0，且在不同侧滑角下，辨识得到的参数 b1均相同，令τ=b1= 0.113，将a0Δβ替换成由风洞数据得到的，可得的传递函数：

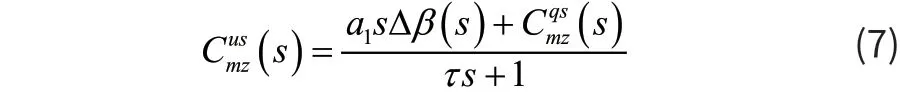
选取CONEX集装箱在速度60kts、旋转速率-151deg/s状态下试飞实测的力系数和风洞试验获得的力系数进行模型参数的确定[5]，则可得到整个速度范围的的传递函数：

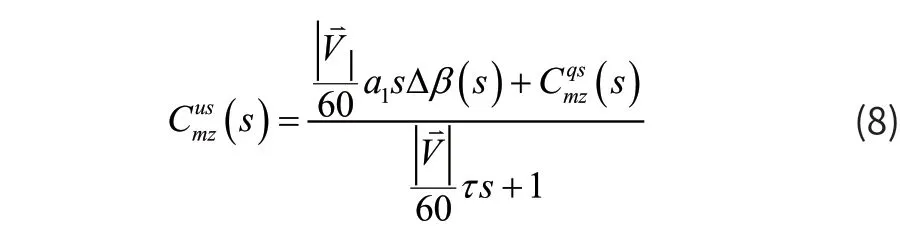
其中为集装箱速度矢量。在速度60kts、旋转速率-151deg/s状态下，由式（8）得到的仿真结果如图2所示。

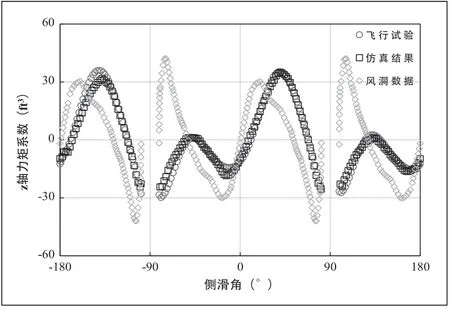
图2 CONEX集装箱仿真结果

用相同方法可得其他气动系数的模型。对于旋转钝体吊挂物，由于约束限制，对其运动特性影响较大的气动力和力矩为x轴、y轴气动力和z轴力矩，其他气动力和力矩计算可直接用风洞数据，则钝体吊挂物气动力和力矩为：

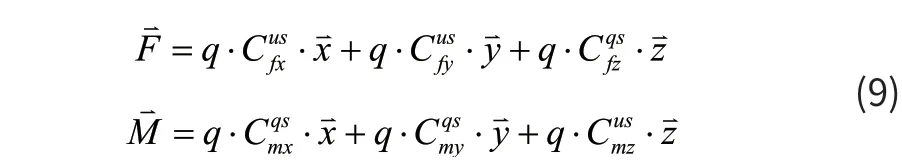
（2）6自由度刚体动力学模型

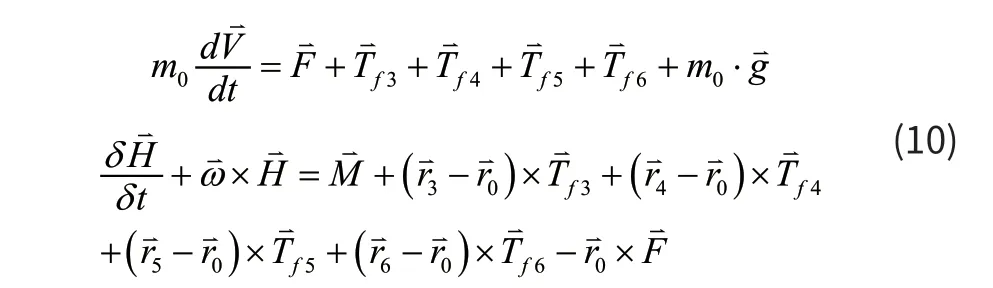
其中为动量矩，为集装箱角速度矢量，m0为集装箱质量。

2 直升机飞行力学模型

2.1 非线性模型

直升机是一个复杂系统，飞行力学建模主要考虑旋翼、尾桨、机身、平尾和垂尾等部件。旋翼建模时考虑了诱导速度的非均匀性和动态特性，桨叶基于叶素理论采用准非定常气动载荷模型，旋翼干扰模型包括旋翼对机身、尾桨、平尾、垂尾和吊挂物的干扰。尾桨建模时采用均匀入流模型，其气动载荷计算基于升力线理论。机身建模采用基于风洞试验数据的准定常气动载荷模型。平尾和垂尾气动模型基于三维流场的二维升力面理论建立，考虑了机身对平尾和垂尾的气动干扰。

本文基于UH-60直升机的基本参数、气动数据建立了直升机非线性飞行力学模型[6]。

城市之间必然会有差异性，每个城市都有自己独特的文化氛围与历史底蕴，因此城市建筑以及规划自然会有所差异甚至是完全不同。但是目前我国城市规划中出现了大量的照搬照抄和拿来主义现象，城市出现规划统一性，根本没有体现本城市的特色所在，这就造成了城市建设的千篇一律，仅仅是制造一座用来居住的城市，而不是制造一座真正具有人文气息的城市。

2.2 控制系统模型

为了在直升机非线性飞行力学模型的仿真中研究钝体吊挂物的稳定性，需要建立飞行控制系统模型。所建立的控制系统模型主要包括姿态保持与控制、航向保持与控制，速度保持与控制和高度保持与控制功能。在直升机-吊挂物耦合系统的非线性响应分析中直升机飞控系统接通姿态保持、航向保持、速度保持和高度保持功能。

3 仿真分析

3.1 参数设置及仿真状态

吊挂系统主吊索长度为1ft，刚度为36723 lbf/ft，阻尼为121 lbf/(ft/sec)。4根分吊索长度均为15.66ft，刚度为9645 lbf/ft，阻尼为22 lbf/(ft/sec)[7]。CONEX集装箱上分吊索挂点3、4、5、6的位置坐标分别为（2.828，4.141，-3.205）、（-2.828，4.141，-3.205）、（-2.828，-4.141，-3.205）、（2.828，-4.141，-3.205），单 位 为ft。吊挂物重量为4550 lbm，直升机重量为16080 lbm。

直升机吊挂CONEX集装箱进行的飞行试验中，吊索构型主要有两类，一类是带有旋转接头，一类是不带旋转接头。由于在悬停时吊挂物就会受到旋翼下洗流的影响而产生绕z轴的旋转运动。对于带旋转接头的吊索构型，直升机以某一速度（40-100kts）稳定前飞时CONEX集装箱会稳定于某一旋转速率（与初始旋转方向相同）；对于不带旋转接头的吊索构型，直升机以某一速度（40-60kts）稳定前飞时CONEX集装箱会以某一旋转速率为幅值做往复旋转。通过对两种吊索构型的试验研究[5]，在本文所建立的旋转接头模型中，仅带有旋转阻尼（即令 0kk= ）时可用于仿真试飞中带旋转接头的吊索构型，仅带有旋转刚度（即令 0cc= ）时可用于仿真试飞中不带旋转接头的吊索构型。

本文所选择的仿真状态为：（1）飞行速度60kts，不带旋转接头（cc= 0），重心位置为=( 0,0,1.3)；（2）飞行速度60kts，带旋转接头（kk= 0），重心位置为⇀=(( 0,−1 .5,1.3)；（3）飞行速度60kts，带旋转接头(kk= 0)，重心位置为⇀ =( 0,0,1.3)。

3.2 仿真结果

吊挂物摆角作为直升机吊挂飞行中最主要的限制条件之一，是研究吊挂物稳定性的重要参数。本文中吊挂物纵向摆角以吊挂点处主吊索拉力矢量在直升机纵向剖面的投影与铅垂线的夹角定义，横向摆角以吊挂点处主吊索拉力矢量在直升机横向剖面的投影与铅垂线的夹角定义。3种典型状态的主吊索摆角和主吊索拉力仿真结果如图3和图4所示。

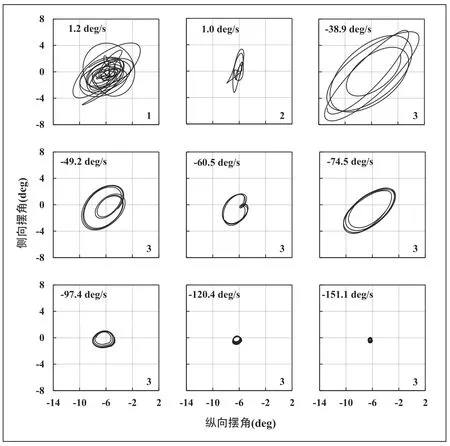
图3 主吊索摆角仿真结果

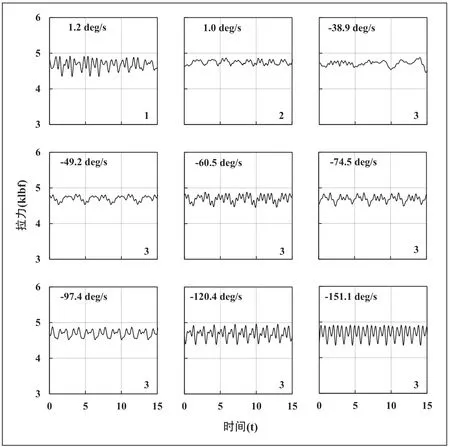
图4 主吊索拉力仿真结果

仿真状态（1）中，CONEX集装箱绕z轴以-148.1~ 151.5deg/s做往复旋转运动，集装箱绕z轴转动的角度范围为-1727.1~1640.0deg，一个周期的平均角速率为1.2deg/s；仿真状态（2）中，CONEX集装箱绕z轴以-53.1~54.7deg/s做往复旋转运动，集装箱绕z轴转动的角度范围为68.6~111.4deg，平均角速率为1.0deg/s；仿真状态（3）中，CONEX集装箱绕z轴以稳定旋转速率持续旋转，调整旋转接头模型中旋转阻尼参数cc，使集装箱旋转速率能够保持在-180.0～-38.9deg/s范围内稳定旋转。

3.3 稳定性分析

CONEX集装箱在不同状态下主吊索纵、侧向摆角、主吊索和分吊索拉力的最大值和最小值随吊挂物平均旋转速率变化情况如图5所示。吊挂物的稳定性取决于纵、侧向摆角的幅值，摆角幅值越大越不稳定。对于仿真状态（3），在旋转速率-180～-74.5deg/s范围内吊挂物的纵、侧向摆角幅值随旋转速率增大而增大，旋转速率从-74.5～-60.5deg/s变化时纵、侧向摆角幅值减小，旋转速率从-60.5～-38.9deg/s变化时纵、侧向摆角幅值增大。摆角幅值在整个旋转速率变化过程中出现了两个极值速率-38.9deg/s和-74.5deg/s。吊挂物的纵、侧向摆角取决于吊挂物的钟摆运动情况，根据直升机上吊挂点与吊挂物重心的距离可得吊挂物的钟摆频率为1.25rad/s。集装箱的气动阻力和侧向力是其钟摆运动的激励，而激励频率与吊挂物的旋转速率有关。当气动阻力和侧向力以180deg为一个周期时（定常气动力是对称的，旋转1周为2个周期），吊挂物的钟摆频率对应的旋转速率为35.8deg/s，仿真状态（3）中旋转速率-38.9deg/s接近钟摆频率对应的旋转速率，摆角幅值为极值；当气动阻力和侧向力以360deg为一个周期时（非定常气动力是不对称的，旋转1周为1个周期），吊挂物的钟摆频率对应的旋转速率为71.6deg/s，仿真状态（3）中旋转速率-74.5deg/s接近钟摆频率对应的旋转速率，摆角幅值为极值。由于气动阻力和侧向力中定常气动力的对称性占主导地位，所以旋转速率为-38.9deg/s时的摆角幅值最大。对于仿真状态（1）和（2），吊挂物在往复旋转时均会经过钟摆频率35.8deg/s，且状态（2）通过该频率时比状态（1）快，摆角幅值较小。从图5中摆动幅值与旋转速率的变化趋势可知，当旋转速率远离钟摆频率时旋转运动与钟摆运动解耦，并抑制钟摆运动。

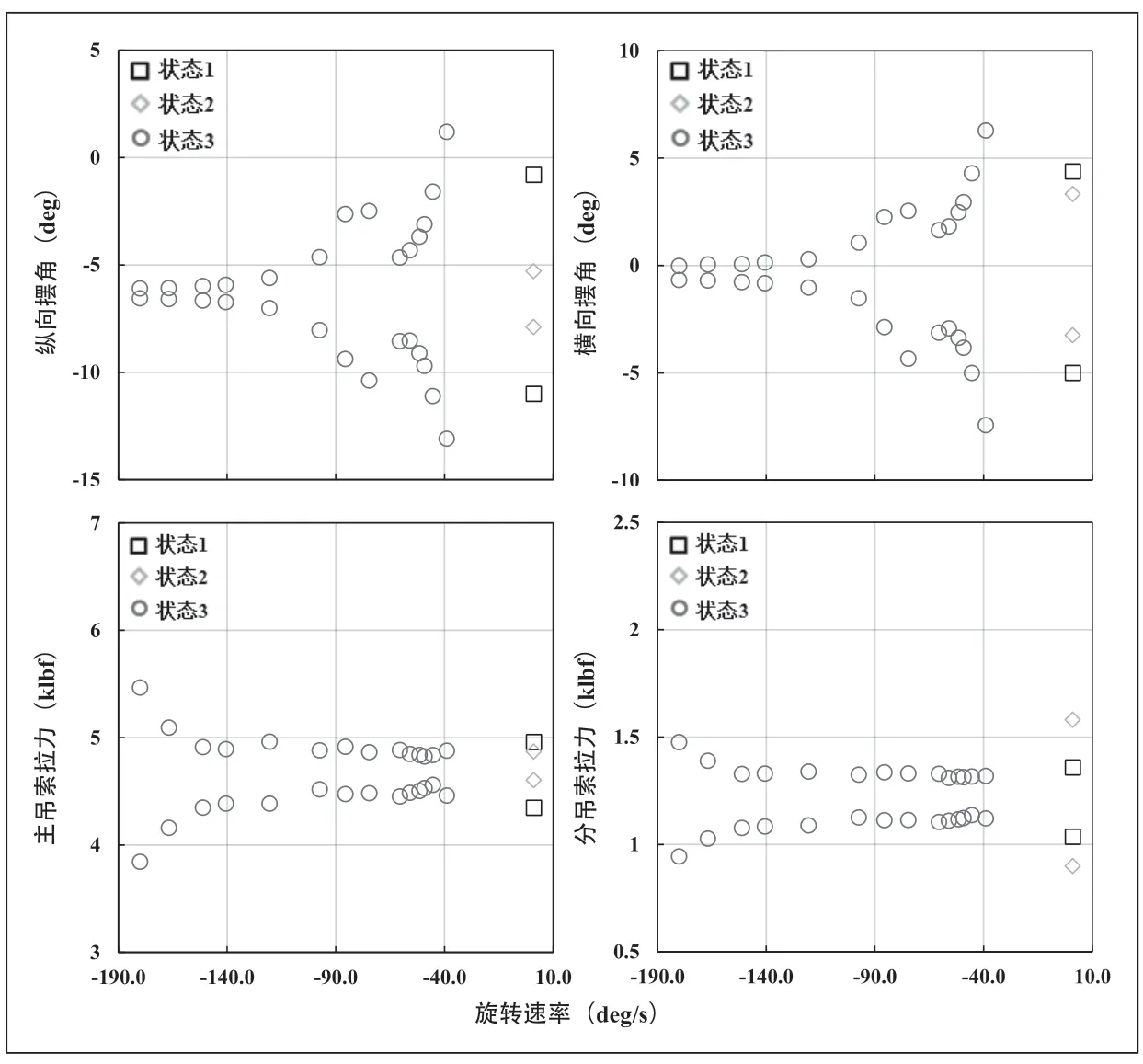
图5 摆角和拉力范围随旋转速率变化情况

对于吊索拉力，除状态（2）中由于重心偏移导致分吊索拉力幅值变大，其余状态在旋转速率大于-151.1deg/s时吊索拉力幅值变化均不大，状态（3）中旋转速率小于-151.1deg/s时索拉力幅值开始有明显增大趋势。吊索拉力幅值与直升机-吊挂物综合体的固有频率有关，由直升机、吊挂物质量和吊索刚度系数可知仿真状态的固有频率为18.2rad/s，吊挂物的升力为激励，激励频率最大为6.3rad/s(对应-180deg/s状态，旋转1周为2个周期)，此时吊索拉力幅值虽增大，但还远小于固有频率。

在试飞中，吊挂物摆动的稳定性往往决定了其吊挂飞行的速度限制。对于单点吊挂构型，从仿真结果来看有两种减弱摆动幅值的途径。一种与状态（2）类似，增加吊挂物的航向稳定性，如在吊挂物上加装阻力伞或尾翼；一种与状态（3）类似，改变吊挂物航向运动特性，使其能够在前飞中稳定旋转，并使旋转速率对应的频率大于钟摆频率，小于直升机-吊挂物综合体的固有频率，如在吊挂物上加装带有两个半球的风速计[8]。

4 结论

本文综合多级吊索模型、旋转接头模型、基于非定常气动载荷的钝体吊挂物刚体运动模型和直升机非线性飞行力学模型建立了直升机吊挂飞行仿真模型，针对几种典型吊挂状态进行仿真，并对吊挂物摆动稳定性进行分析。结果表明：

(1)基于非定常气动载荷建立的钝体吊挂物仿真模型在前飞状态中表现出航向不稳定性，与试飞结果相符。

(2)当钝体吊挂物稳定旋转的频率大于吊挂物钟摆频率时，旋转运动能够有效抑制吊挂物纵、侧向的摆动幅度。

(3)在前飞时增加钝体吊挂物的航向稳定性或者使其以一定频率稳定旋转都能够有效改善吊挂物的摆动稳定性，扩大该吊挂构型的前飞速度包线。