一种综合射频系统频谱调度决策算法

薛军帅 张 迪 黄 勇 杨凯栋

（西安电子工程研究所，陕西 西安 710100）

随着战场环境日益复杂化，射频功能性需求逐增，原有的单一波段、功能、体制电子设备简单堆积凸显出占用空间大、功耗高、天线及结构繁杂、相互间易产生电磁干扰等问题[1]，因此综合射频系统被逐步应用于机载、舰载、车载以及弹载等领域，其有效集成了感知、侦察、干扰以及通信等功能[2-3]。综合射频系统内部频谱的相互关联度显著提升，且频谱的提供能力也显著提升。原有独立分割存在的系统间简单频率规避在处理综合射频系统工作需求、内部与己方信号杂散、外部动态频谱环境等信号参数方面，存在着规避内部复杂互扰和交调效果差、资源浪费显著等问题，已不能满足综合射频系统频谱决策的需求。针对该项需求，本文从综合射频系统频谱决策着手，构建优化模型，开展系统频谱资源调度优化算法，从而形成快速的系统频谱配置策略和程序。

1 幅度权重优化模型

表1 主信号A、B 的频率权重

混频信号的频率F 通过如式（1）的各频点加权获得：

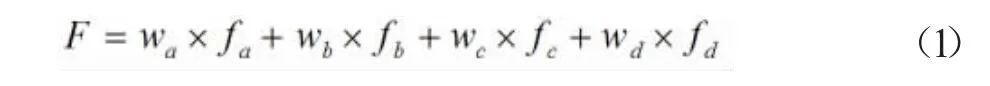
式中，wa、wb、wc和wd分别代表频点a、b、c 和d 的频率权重。fa、fb分别代表频点a 和b 的频率并且频点fa和fb的取值如下式：

混频频率的权重的取值范围是在-10～10 之间（以1单元为步长），进一步讨论频率大于等于0 GHz、小于等于FmaxGHz 的频点。为减少混频信号对主信号的干扰，我们期望除主信号A、B 外其他混频信号的幅度值R 低于幅度阈值RmaxdB，主信号带外会出现高于幅度阈值的杂散频点（混频信号），带外杂散信号可以通过开关滤波器组滤除。混频信号的幅度计算如下式：

合理幅度权重调整，能降低系统搭建成本，方便布局。因频点增多，人工调整幅度权重的效率越来越低并给主信号带来不可避免的干扰，为解决这种多变量问题，考虑目标：最大化危险混频信号与主信号的欧式距离和最小化危险混频信号总数。为简化问题便于获取最优幅度权重分布，将上述两个目标加权，并建立如下优化模型：

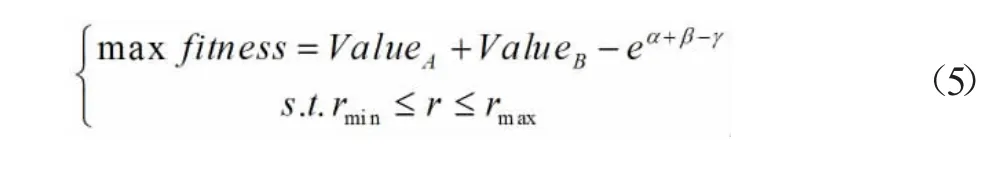
式中，

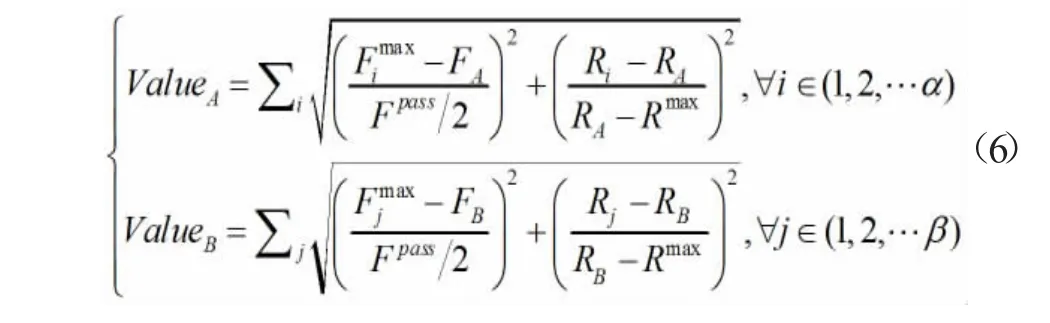
式中，rmax和rmin分别为幅度权重的最大值和最小值；Fipass和Ri分别代表频率落在滤波器通带内并且幅度高于幅度阈值的混频信号i 的频率和幅度（注：这类信号统一定义为危险混频信号）；ValueA是在主信号A 附近的危险混频信号与主信号A 的频率和幅度归一化的欧式距离；α 表示主信号A 的危险混频信号的总数；ValueB代表在主信号B 附近的危险混频信号与主信号B 的频率和幅度归一化的欧式距离；Fjpass和Rj分别表示危险混频信号j 的频率和幅度；β 是主信号B 的危险混频信号的总数；γ 是可调系数，根据实验调节。

2 混沌粒子群优化算法

粒子群优化算法是一种具有实现简单、运算速度快，且具备一定局部和全局搜索灵活性的随机寻优算法，但该算法结果可能会陷入局部最优。混沌映射具备的遍历性与PSO 结合可提升算法有效性[4]。把幅度权重作为决策变量，即粒子群位置信息，采用混沌粒子群优化（Chaotic Particle Swarm Optimization，CPSO）算法解决模型[5]。

3 频率优化模型

3.1 最优频率模型

考虑频点a 和b 的频率是可调的，并且从公式（1）中可以看出双方都受主信号A 频率的影响，由主信号A 和频点b 的频率可以推算频点a 的频率。主信号A 的频率是已知项，系统此时可以通过调整频点b 的频率减少带内不必要的干扰信号。参考模型（5）建立如下优化模型：

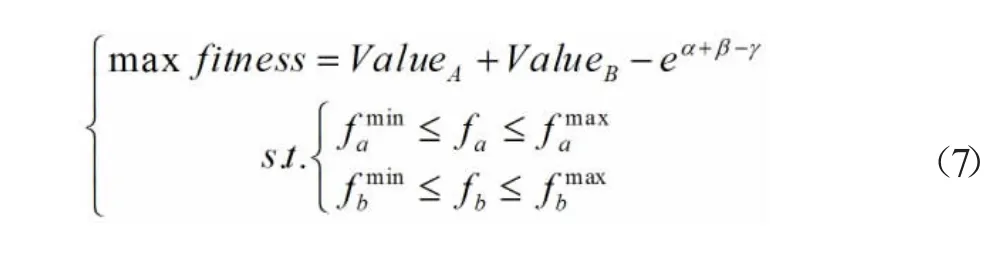
针对模型（7）采用CPSO 算法。上述问题显示频点b可作为唯一可调变量，故本文将频点b 的作为决策变量，即CPSO 算法中的个体的位置信息，根据混沌粒子群算法的特性能够保证频点b 的频率的分配始终在规定范围内，但是fa因fb变化而变化，存在导致fa超出预设频率范围的可能性。为克服这一问题，模型（7）将被惩罚函数重构，具体如下式：

式中，δ 为惩罚因子，其值根据经验选取。

3.2 频谱决策模型

现有感知技术能辨别各种干扰信息，为综合射频系统的频谱决策提供便利。在干扰信息少且备选频带宽的情况下，通过简单枚举就能实现主信号A 的最优的频率选择；但在系统被大量干扰信号影响的情况下，枚举法效率低。

为解决上述问题，本文将主信号A 与干扰信号之间的频率和幅度的差值作为衡量频率分配合理性的准则。由于主信号A 的带宽为F，故只考虑与主信号A 频率相距±F/2 的干扰信号，主信号A 与己方干扰信号频率和幅度的归一化的欧式距离Distance；主信号A 与敌方探测和干扰信号频率和幅度的归一化的欧式距离分别为Distance和Distance。参考模型（1），上述问题可以被考虑为如下模型：

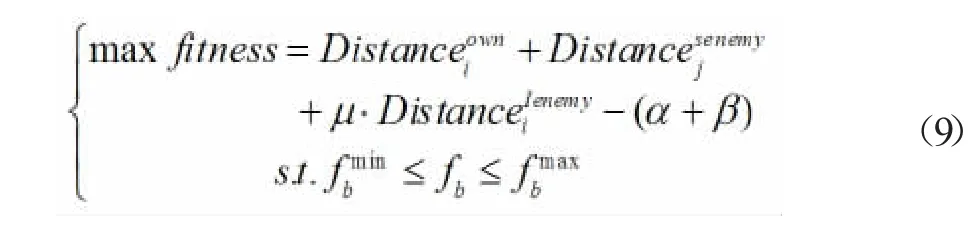
式中，μ 为加权系数，帮助主信号A 避开敌方干扰。

4 最优频谱计算

4.1 最优幅度权重

为保证最优的幅度权重分配适用性高，实验考虑频点a 分配频率的5 种不同场景，定量考虑频点b、c 和d具体分配见表2。实验讨论的滤波器通带Fpass=1.5GHz 并且综合考虑对5 种场景的适应度函数加权求和，然后通过CPSO 算法获得最优幅度权重分配方案。

表2 5 种场景的各频点频率分配

根据最优幅度权重我们可获得主信号以及混频信号详细的数据见表3。

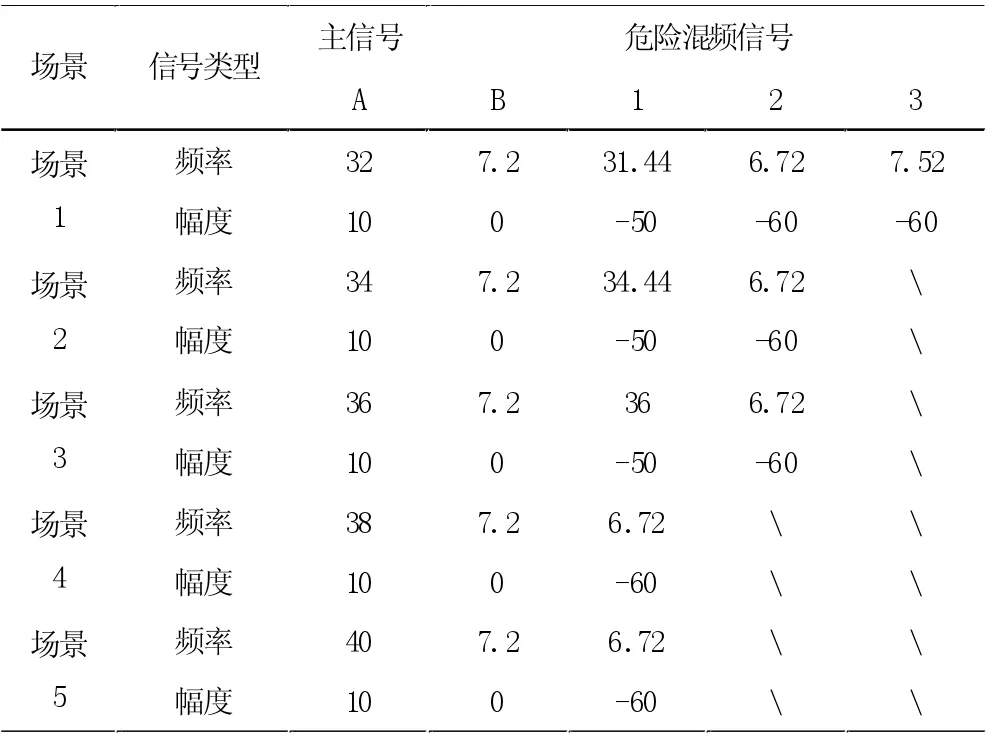
表3 主信号和异常混频信号

通过仿真获得最优的幅度权重分配方案，为射频综合的设计提供了极大便利。随机的频率分配会影响射频综合的性能，如4 个频点的频率分配为f =[15.68,7.2,1.44,2.4]时，获得表5（1），主信号A 的频率为40GHz 与场景5 相比较可以发现，此时的频率分配产生的危险混频信号的总数为3，多于场景5 的1 个；另当f= [12.08,6.4,1.44,2.4]时，获得表4（2），与场景1 表3 相比较，此时的危险混频信号总数为2，少于结果显示场景1的3 个。可见合理频率分配能减少危险混频信号个数。

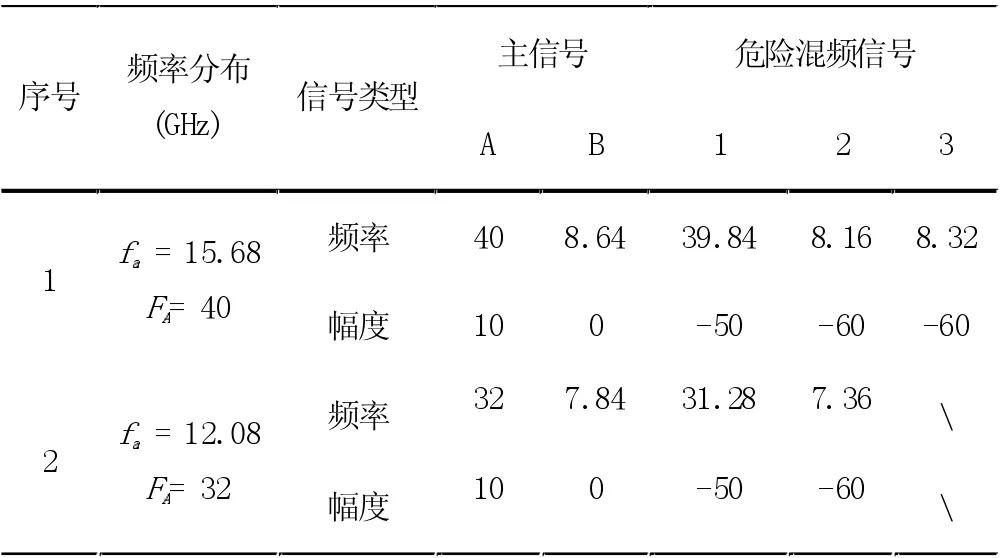
表4 主信号和危险混频信号的统计

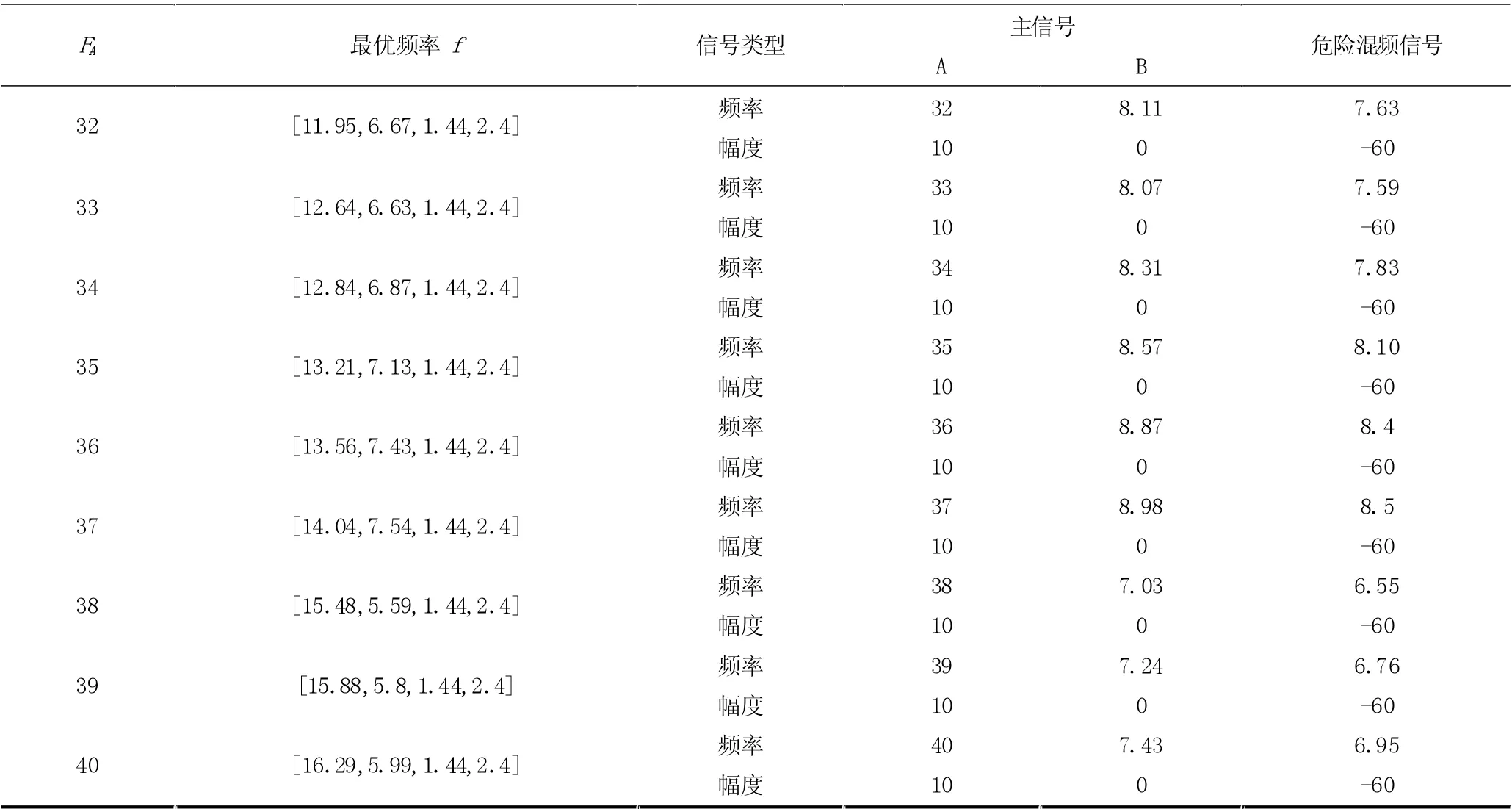
表5 主信号和危险混频信号的统计

4.2 最优频率

在硬件设计中，幅度权重已固化，此时幅度权重为最优幅度权重。采用CPSO 算法，频点a 的频率参数设置为：[9, 20]；频点b 的频率参数设置为：[3, 8]。本文考虑主信号A 的频率分别为32～40GHz 整数频点的最优频率分配以及危险混频信号的信息。应用CPSO 算法仿真结果见表5。

5 结论

为规避不必要的系统内部干扰，根据需求采用粒子群优化算法调节频点频率，能减少系统内部的互扰和交调。根据系统感知反馈的环境信息，CPSO 算法能够帮助系统在复杂干扰环境下选择最优频率，最终实现频率资源配置策略和整机系统的闭环连接。后期可在主信号对应频点的最优频率分配已固定基础上，进一步研究通过大量最优频率分配数据对BP 神经网络离线训练，实现主信号和对应频点最优频率分配的映射，进而减少计算量、降低时延对系统的影响。