基于序列信息的酶的亚类多特征参数识别方法

王 婷

(长治职业技术学院 山西长治 046000)

0 引 言

酶是人体健康的源泉，它几乎参与所有的生命活动，如消化、呼吸、睡眠、思考、情绪、内分泌等。人体的生长和延续需要成千上万种以上的酶化反应来实现。根据酶所能催化反应种类的不同，将酶分为6个家族类：氧化还原酶、转移酶、水解酶、裂合酶、异构酶和合成酶[1-2]。按照国际科学文献中的分类原则，在这6个家族类的基础上，再根据底物中被作用的基团或键的特点进一步将每个家族分为不同的亚类[3]。酶的结构及作用机理与其所属的家族类或亚类关系密切，因此对酶分类问题的研究十分必要。近年来对酶的家族类的分类研究已经比较完善，故如今的热点变为了酶亚类的分类预测。

本文基于酶的序列信息，分别使用矩阵打分与离散增量的方法提取各类特征参数，然后将多种特征参数有效组合，利用支持向量机分类算法对数据集中酶家族类的各个亚类进行分类识别。计算结果表明，此算法能够获得较高的预测成功率。

1 材料与方法

1.1 数据集的选取

本文使用的酶序列来源于ENZYME数据集http://www.expasy.org/enzyme/(released on 01-May-2007)，和Chou等人使用的数据集相同[4]。按照以下3个标准来选取数据集：①选取长度均大于50个残基的序列；②删除同时属于多种类型的酶序列；③酶序列的相似性小于40%。基于以上标准可以得到： 18个亚类的1820条氧化还原酶序列；8个亚类的2847条转移酶序列；5个亚类的3279条水解酶序列；6个亚类的892条裂合酶序列；6个亚类的639条异构酶序列；6个亚类的965条合成酶序列。

1.2 计算方法

1.2.1 矩阵打分方法

矩阵打分方法已被成功应用于蛋白质β-发夹模体的识别[5]、蛋白质折叠子的预测[6]等方面。由于酶序列片段具有很强的位点保守性，故使用矩阵打分方法来提取特征参数，此方法的应用分为以下4步。

这里，i = 1,2,…, L (L为酶序列片断的截取长度)，j表示20种氨基酸和1个空位，iN表示在第 i个位置氨基酸出现的总频数，ijn表示在第i个位置第j种氨基酸出现的频数[7]。

②依据位点的位置概率，构造21行L列的位置权重矩阵：

其中，0jP 表示第j种氨基酸的背景概率[7]。

③计算酶序列中第i个位点的保守性参量：

④使用位置权重矩阵，对于任意一段给定的酶序列片段进行打分，定义打分函数(S)为：

其中，,maxiw 和,inimw 分别表示第i行矩阵元的最大值和最小值，这里0 1S≤ ≤ 。

以氧化还原酶为例，利用氧化还原酶包含的18个亚类的数据集可以得到18个位置权重矩阵，对于任意一段给定的酶序列片段，由(4)式可以得出18个打分值，比较这18个分值的大小，哪一个亚类的分值高，此序列片段就被判断为属于哪一类别的亚类。类似的，转移酶、水解酶、裂合酶、异构酶和合成酶分别也据此判断。

截取酶序列片段的原则：①由于酶序列的N端与C端所反映的位点保守性差异很大，需分别从酶序列的N端与C端截取氨基酸片段进行矩阵打分的分类预测，通过比较，选取包含70个氨基酸残基的片段长计算效果最佳；②为了不影响计算结果，对酶序列的长度作了统计分析，如表1所示，发现序列 长≤140个氨基酸残基的序列数在各类中都＜6.13%；③以氧化还原酶为例，从酶序列的N端和C端分别截取70个氨基酸残基的片段长进行打分，任意一条待测序列得到18×2个打分值。类似的，转移酶、水解酶、裂合酶、异构酶和合成酶分别可以得到 8×2、5×2、6×2、6×2和6×2个打分值。

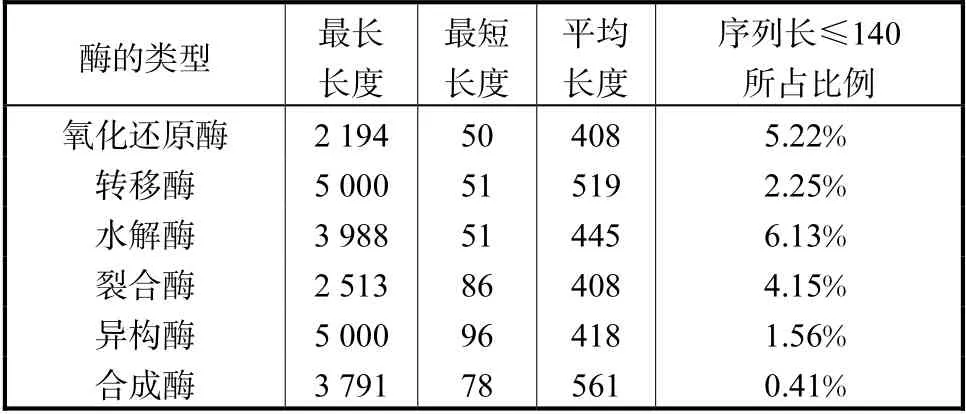
表1 酶的6个家族类序列长度的统计分析 Tab.1 Statistical analysis of sequence length of six families of enzymes

1.2.2 离散增量方法

近年来离散增量方法已在亚细胞定位[8]、蛋白质超家族的预测[9]等工作中大量使用。

在S维空间中，构造2个离散源X：[n1，n2，…，ni，…，ns]和Y：[m1，m2，…，mi，…，ms]，这里ni和mi分别表示第i种氨基酸关联出现的频数，它们的离散量分别为：

离散增量定义为：

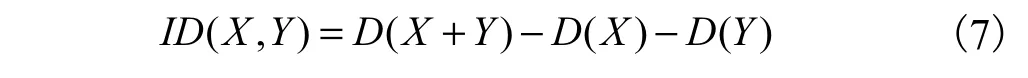
其中，D ( X + Y)为混合离散源X+Y(n1+m1，n2+ m2，…，ns+ms)的离散量，，对数的底b＝10，离散量的单位为哈特。

离散增量定义了2个离散源的同源性程度，离散增量值越小，它们之间的相似性越高[7]。

以氧化还原酶为例，由其18个亚类的数据集可以构成18个标准离散源，对于任意一条酶序列，由(7)式可以求得18个离散增量值，比较它们的大小，哪一个亚类的离散增量值小，此序列就被判断为属于哪一类别的亚类。类似的，转移酶、水解酶、裂合酶、异构酶和合成酶也适用。

根据氨基酸残基的物理化学、生物化学性质的不同，将20种氨基酸分为以下9类[10]：C；M；N、Q；D、E；S、T；P、A、G；I、V、L；F、Y、W；H、K、R。

本文以酶序列中氨基酸理化性紧邻关联与氨基酸次邻关联的出现频数分别构成标准离散源，均计算离散增量值。以氧化还原酶为例，利用氨基酸理化性紧邻关联的出现频数为参数可以得到18个标准离散源，对于任意一条待测序列可以得出18个离散增量值；同样以氨基酸次邻关联的出现频数为参数也可以得到18个离散增量值。类似的，转移酶、水解酶、裂合酶、异构酶和合成酶分别可以得到8×2、5×2、6×2、6×2和6×2个离散增量值。

1.2.3 支持向量机方法

支持向量机(SVM)是一个非常强大且具有多种功能的机器学习模型，能够处理线性或非线性分类问题。SVM是最好的现成分类器(现成指不用修改可以直接使用)，而且它的分类错误率较低。SVM特别适合应用于中小型规模数据集样本的分类问题，能够解决高维问题，还可以避免神经网络结构选择和局部极小点问题[11]。本文使用的是台湾大学林智仁等人开发的libSVM-3.1版的程序包[12]。libSVM提供了一些简单易用的接口，使用户能够方便应用而不必关心其内部复杂的数学模型和运行过程。

2 结果与讨论

以氧化还原酶为例，对任一待测的酶序列，把氨基酸理化性的紧邻关联与氨基酸的次邻关联分别的出现频数作为特征参数，使用离散增量方法得到18×2个离散增量值；分别从酶序列的N端与C端截取70个氨基酸残基片段长进行矩阵打分，得到18×2个打分值；将这36个离散增量值与36个打分值构成的组成向量，共同输入支持向量机中，使用刀切法(Jackknife)检验对氧化还原酶中的亚类进行分类识别，其预测结果见表2。类似的，对其他5个家族类的酶的亚类也做了同样的分类识别，预测结果在表2中列出。此外，为了方便预测结果的比较，还分别采用前面介绍的矩阵打分方法和离散增量方法对酶家族类的亚类进行预测，同时将Chou等[4]运用相同数据集的Jackknife检验的预测结果也列于该表中。

表2 酶的6个家族类中各亚类的Jackknife检验下的预测结果 Tab.2 Prediction results of each subclass in six families of enzymes under jackknife test

续表2

从表2的预测结果能够看出，从酶序列的N端和C端截取氨基酸残基片段的矩阵打分方法预测结果整体上优于离散增量方法的预测结果，进一步表明酶序列的两端具有很好的位点保守性。而矩阵打分的2种分值结合氨基酸关联的2种离散增量值共同作为特征参数进行有效的组合，利用支持向量机的分类算法，获得了最佳的预测结果。不但每个家族类的总体预测成功率很高，而且各个亚类的结果也非常理想。氧化还原酶、转移酶、水解酶、裂合酶、异构酶和合成酶中亚类的总体预测成功率分别为96.43%、92.90%、90.85%、99.22%、99.84%和98.86%。氧化还原酶、异构酶和裂合酶的总体预测成功率比Chou[4]的方法分别提高了9.73%、6.54%和4.82%，水解酶和转移酶的总体预测成功率比Chou等[4]的结果稍差。究其原因，是因为水解酶和转移酶的序列数目很大，故噪声显著。由于支持向量机需要大量的内存，选择正确的核很重要，所以很难做出调整，当数据集的噪声较大时，无法获得满意的结果。

3 结 语

本文基于酶的序列信息，使用多特征的组合向量作为参数对酶的亚家族类进行类型识别，预测成功率有了很大提高。这是因为支持向量机方法具有高效的分类能力，它能够将各种序列信息有效融合，通过网格化寻找最优参数c值和g值。此方法的优势还表现在通过提取矩阵打分值和离散增量值的方法，降低了输入支持向量机的特征参数维数，避免了维数灾难，简化了计算过程。■