天然气管道射流火焰危害影响维度分析

2022-04-20杨健许宁周星黄澔诸葛伟郝永梅

石油与天然气化工 2022年2期

杨健许宁周星黄澔诸葛伟郝永梅

1.常州港华燃气有限公司 2.常州大学环境与安全工程学院

随着城市发展规模的不断扩大，天然气的用量需求越来越大，管道运输作为最经济、安全的天然气运输方式，天然气管道成为城市发展不可或缺的基础设施之一[1-2]。目前，我国服役年龄在25年以上的输送管道已超过60%，大量的管道已进入故障多发期。管道故障后泄漏的天然气遇到火源极易引发火灾爆炸事故，会造成人员伤亡和财产损失，从而导致一系列的经济和社会问题[3-4]。

天然气管道泄漏一般引发火球、射流火焰、蒸汽云爆炸等事故类型，其中，射流火焰是最易发生的事故类型。射流火焰一般由高压储存天然气泄漏遇点火源形成，其后果往往呈现破坏范围广、威力大等特点[5-6]。国内外很多学者已对射流火焰及其事故危害进行了研究,雷婷等[7]对分离器典型泄漏孔径下的射流火焰进行了特性研究；王莉莉等[8]建立数学模型，解出射流火焰危害半径，并分析泄漏孔径和危害半径的关系；黄平等[9]结合具体案例，通过Fluent软件模拟，计算出不同条件下的射流火焰长度及热辐射分布情况，最后进行事故风险评估；周魁斌等[10]根据不同模型,将其耦合成一种更加科学的射流火焰计算模型，可以应用于不同泄漏状况；T. Bajcar等[11]建立了天然气计量站风险评估系统，补充了射流火焰风险评估模型；S. J. Tong等[12]建立射流火焰模型，借助MATLAB计算机辅助程序计算，结合相关的数据形象描绘伤害图；Y. Zhao等[13]利用有限体积法求解流动方程，预测了射流在空气中的演化，采用k-ζ湍流模型进行计算。

总体来看，国内外研究人员对射流火焰的研究，大部分是关于管道泄漏引起的射流火焰事故，一般默认选取竖直状态，而现场实际情况的泄漏孔可以朝向不同的角度，对这方面的研究也相对缺乏，导致对不同方向射流火焰危害范围的评估所做的探索非常有限。

鉴于此，为了探究天然气管道泄漏角度对射流火焰的影响，进一步提高射流火焰的危害范围评估的精确性，本研究利用FDS分别模拟天然气以与水平方向夹角为0°、30°和90°泄漏并引发射流火焰的情况，将模拟结果与传统理论模型及改进后的评估模型分别进行对比，分析这3种情况下的射流火焰特性和危害范围，并为应对不同情况的应急工作提供参考。

1 理论模型

1.1 泄漏速率计算模型

泄漏速率是计算天然气射流火焰伤害范围的重要参数，射流火焰的火焰几何尺寸和辐射强度均与泄漏速率相关[14]。根据内外压力的比值，确定气体泄漏是声速流动还是亚声速流动，两种流动方式对应两种泄漏速率模型，代入环境条件参数，可求得泄漏速率，并作为FDS模拟的初始变量。

(1)

(2)

式中：p0为管道外环境压力，Pa；p为管道内压力，Pa；k为气体绝热指数，天然气一般取1.306；Q为泄漏速率，kg/s；Cd为气体泄漏系数，圆形泄漏孔取1.00；M为气体摩尔质量，kg/mol；T为气体初始温度，K；A为裂口面积，m2；R为气体常数，J/(mol·K)，取8.314。

1.2 不同角度射流火焰的几何特性分析

射流火焰的热通量与火焰几何特性有关，之前研究火焰几何特性主要考虑火焰长度，然而管道不同泄漏角度(孔轴线与管道水平面的夹角)也是重要影响因素，因此射流火焰的危害分析应将管道泄漏角度考虑进去。火焰长度一般是指有风状态下的长度，与无风状态下的火焰长度相关。火焰长度是从泄漏燃料出口边缘到最远的下游位置之间的轴向距离，其中的火焰尖端对人眼可见[15]。

有风状态下射流火焰长度计算公式如下：

Rb0=Y×Ds

(3)

(4)

Ds=[4×Q/(π×ρ0×uj)]1/2

(5)

Lb=Lb0×(0.51×e-0.4uw+0.49)×

[1-0.006 07×(θ-90°)]

(6)

式中：Lb为有风状态下射流火焰长度，m；Lb0为无风状态下射流火焰长度，m；Ds为燃烧等效直径，m；Q为气体泄漏速率，kg/s；ρ0为空气密度，kg/m2；ρ气为气体密度，kg/m2；A为裂口面积，m2；uw为风速，m/s；uj为射流速度，m/s；θ为孔轴线与管道水平面的夹角，0°～90°；Y为比例系数(射流火焰长度与其直径呈一定的比例关系)。

式(3)中Y通过式(7)求得：

(7)

式中：Cb为常数0.2；Ca、Cc为中间变量，由如下公式求得：

(8)

(9)

(10)

式中：g为重力加速度，m/s2；M为气体摩尔质量，kg/mol；F为燃烧气体质量所占的比例，%。

1.3 不同射流角度的危害计算模型

射流火焰对周围建筑物及人员的危害主要是热辐射，可使周围的设施燃烧破坏，发生一系列的连锁反应，致使火灾蔓延扩大，造成更多的财产损失和人员伤亡。由此看出，射流火焰热辐射危害范围远大于火焰本体造成的危害范围。因此，在对射流火焰几何特性进行分析后，需进一步计算热通量，并计算出伤害半径[15]。

(1) 热通量计算公式如式(11)所示：

(11)

式中：I(r′)为目标接收到的热通量，kW/m2；η为效率因子，一般取0.2；Q为泄漏速率，kg/s；r′为目标与火焰中心之间的距离，m；Tjet为辐射率系数，射流火焰一般取1；He为可燃气体燃烧发热量，kJ/kg，天然气的一般取5.56×104kJ/kg；R1为火焰锥体长度，m。

为了简化计算，通常可将式(11)简化如下：

(12)

(2) 危害半径计算公式如式(13)所示：

(13)

由式(12)、式(13)可知，以前关于射流火焰研究基本没有考虑射流的角度，本研究的意义是在原来射流火焰计算模型的基础上，增加泄漏角度的参变量，让原来的计算模型更符合现场实际情况。改进后模型如下。

危害半径与射流火焰长度及射流角度相关。

当r≤Lb×tanθ时：

(14)

式中：ra为改进后的危害半径，m；θ为泄漏孔轴线与水平方向的夹角，(°)。

将式(13)代入式(14)中，得到：

(15)

当r>Lb×tanθ时：

(16)

将式(13)代入式(16)中，得到：

ra=Lb×cosθ+

(17)

2 射流火焰数值模拟

2.1 模型构建及边界条件

采用FDS软件进行模拟研究，研究的泄漏管道见图1。管道规格为DN150 mm，钢制(表面镀锌)。模拟真实开敞环境，延Y轴管道建模，管道三维模型如图2所示。将3种情况中位于管道中心截面的3点钟、2点钟和12点钟位置处的泄漏孔分别命名为孔1、孔2和孔3，其泄漏方向分别与X轴正方向成0°、30°和90°的夹角。

模拟设置管内气体温度30 ℃、环境温度20 ℃、环境风速1 m/s、管内压力4.0 MPa、管道外压力为标准大气压，模拟实验通风状态。根据现场实际情况，除去地面，其他5个面设置为通风面。本次射流火焰模拟小孔泄漏，泄漏孔径为20 mm。根据第1节模型公式，通过管道内外比值确定此次泄漏为声速泄漏，确定泄漏速率为0.215 kg/s。

2.2 不同角度射流火焰几何特性分析

在FDS模拟环境下，火焰喷射过程中形成燃烧云，射流火焰在2.92 s时，在压力作用下高度超过50 m，在4.06 s时射流火焰趋于稳定。当泄漏方向与水平方向成30°夹角时，天然气在泄漏时受周围压力差抬升作用的影响向Z轴正方向倾斜。射流火焰在3.31 s时形成完整的蘑菇云，在4.98 s时射流火焰趋于稳定，且火焰高度突破50 m。当水平泄漏时，射流火焰喷射出去，4.08 s时在喷射朝向处形成燃烧云团，5.73 s时火焰喷射顶端有涡流出现，火焰顶部有明显波动，出现多个涡流组成的浮力驱动满流火焰，火焰长度缩短。由于喷射孔不断喷射燃气与空气混合燃烧，火焰长度成周期变化。

由X-Z平面温度切片得到各射流火焰稳定后的温度分布如图3所示。

2.3 温度场分析

由图3切片温度可知，3处泄漏口模拟火焰最高温度均在1 000 ℃左右，位于射流火焰顶部及火焰面。泄漏孔附近基本上没有天然气燃烧现象，天然气向外急速喷射，空口处天然气浓度不适合燃烧，空口处温度不是很高，但是存在速度流场，气体在喷射出去过程中，随着能量的消耗，气流速度逐渐减小，并且流场由较小的区域向四周扩散[17]。由第2.3节可知3种情况射流火焰在燃烧6 s后均趋于稳定，以15 s时收集到的数据为例，数值模拟中由各热电偶收集到的射流火焰稳定燃烧后的温度数据见表1。

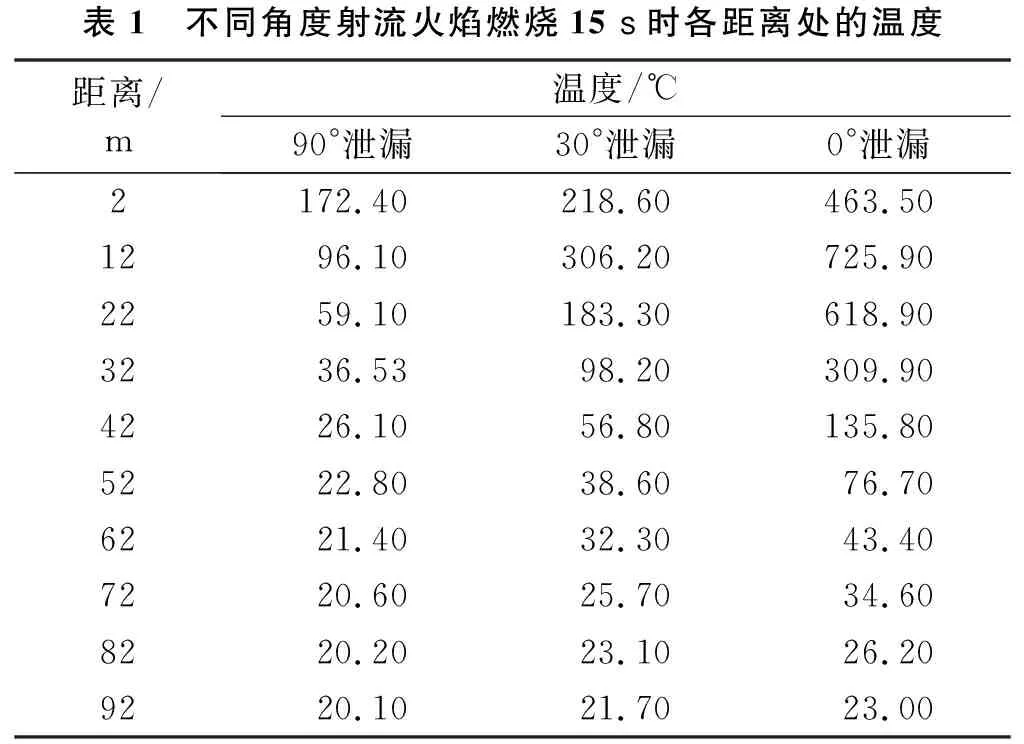
表1 不同角度射流火焰燃烧15 s时各距离处的温度距离/m温度/℃ 90°泄漏 30°泄漏 0°泄漏2172.40218.60463.501296.10306.20725.902259.10183.30618.903236.5398.20309.904226.1056.80135.805222.8038.6076.706221.4032.3043.407220.6025.7034.608220.2023.1026.209220.1021.7023.00

2.4 热辐射分析

在数值模拟中可通过设置热辐射监测装置进行收集，由第2.3节可知各角度射流火焰在燃烧6 s后均趋于稳定，以15 s时收集到的数据为例，数值模拟中由图3中各热辐射监测装置收集到的射流火焰稳定燃烧后的热通量数据见表2。

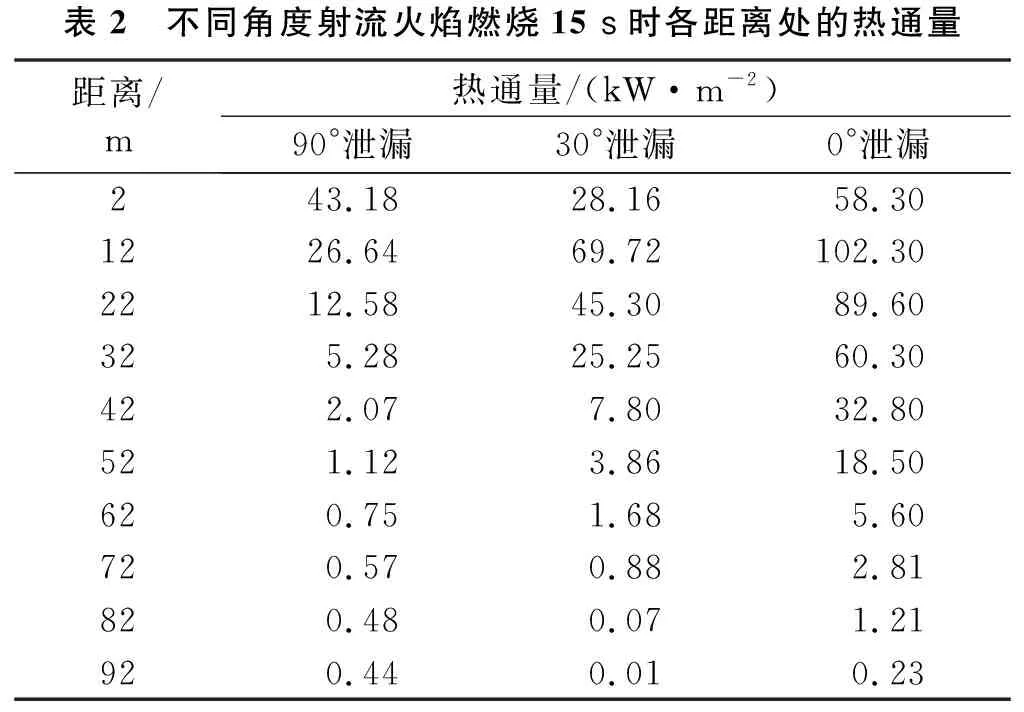
表2 不同角度射流火焰燃烧15 s时各距离处的热通量距离/m热通量/(kW·m-2) 90°泄漏 30°泄漏 0°泄漏243.1828.1658.301226.6469.72102.302212.5845.3089.60325.2825.2560.30422.077.8032.80521.123.8618.50620.751.685.60720.570.882.81820.480.071.21920.440.010.23

3 危害分析

人员或者设备接受热量都会有一个临界值，为了方便比较评估，一般对照热通量准则，目标接收到热通量超出对应标准则会受到相应程度伤害[18]。根据模拟时监测装置收集到的热通量数据，对比天然气工艺装置设施的火灾热辐射破坏标准值[19]，确定伤害半径和设备损坏半径，结果如表3所列。

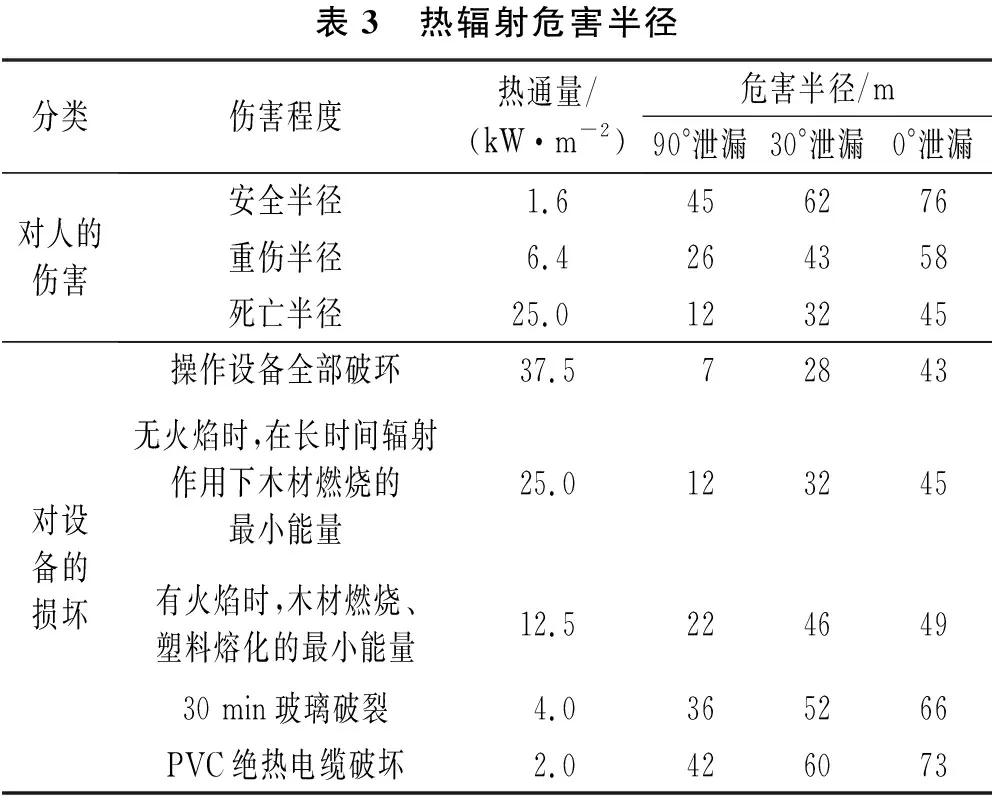
表3 热辐射危害半径分类伤害程度热通量/(kW·m-2)危害半径/m 90°泄漏 30°泄漏 0°泄漏对人的伤害安全半径1.6456276重伤半径6.4264358死亡半径25.0123245对设备的损坏操作设备全部破环37.572843无火焰时,在长时间辐射作用下木材燃烧的最小能量25.0123245有火焰时,木材燃烧、塑料熔化的最小能量12.522464930 min玻璃破裂4.0365266PVC绝热电缆破坏2.0426073

同样，选取以人为对象时的危害范围评估数据，将上述模拟结果与改进后的危害范围预测理论的计算结果进行对比，对比情况如图4所示。

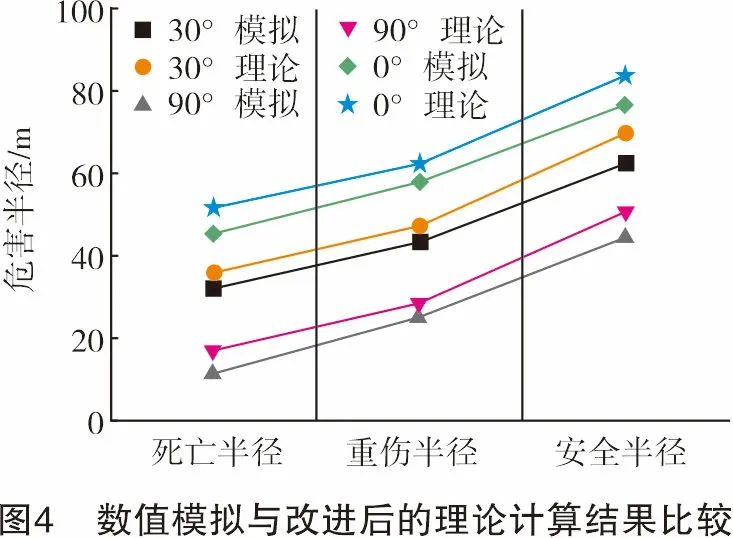
由图4可以看出，由改进后的危害范围预测模型计算的危害范围与模拟数据吻合度较好，但二者仍然存在误差。其主要原因为数值模拟收集的热通量为距地面1.8 m高处而并非与管道同一水平面上的热通量，因此模拟所得的危害范围稍小于改进后的理论计算值。

同时，由表1可知，天然气以90°方向泄漏时，火焰在竖直方向上喷射，减小了辐射范围，因此与另外两种方向的射流火焰相比，同等严重程度的危害半径更小。由于热辐射收集装置分布于距地面1.8 m高的水平线上，距离90°方向的射流火焰更远。因此，该管道90°泄漏时的危害半径最小。

在3种情况中，天然气以0°方向泄漏引起射流火焰的危害最大，死亡区域是以51.3 m为半径的圆，重伤区域是内圆半径51.3 m、外圆半径61.8 m的圆环区域。以此类推，轻伤区域与安全区域的边界线为半径82.7 m的圆。天然气以30°方向泄漏引起的射流火焰，从死亡到安全，边界线分别为以半径35.5 m、47.4 m、69.5 m的圆环。可见，这两种方向的射流火焰危害半径较为接近，这是因为30°的角度较小，天然气以30°方向泄漏时，重力作用使得泄漏气体的运动轨迹接近0°泄漏的气体运动轨迹。