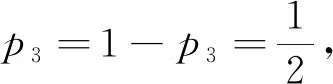随机五角链和随机螺旋五角链的指标①
2022-04-20张海东王维忠
张海东,王维忠
兰州交通大学 数理学院, 兰州 730070
本文考虑的图均为简单无向连通图. 设图G的顶点集为V(G)={v1,v2, …,vn}, 边集为E(G). 记dv为图G中顶点v的度, 且(di,dj)表示度分别为di和dj的两顶点间的边, 图G中边为(di,dj)的数目记为mdidj(G), 其他符号可参见文献[1].
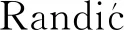
若连通图G中任意顶点的度小于5, 则称其为分子图. 文献[3]研究了随机聚苯链的Wiener指标, 之后文献[4]分别定义了α,β,γ-随机五角链. 受文献[5]的启发, 本文引入随机螺旋五角链, 即将α-随机五角链的所有割边收缩之后所成的随机五角链.
1 随机五角链的指标


图1 α-五角链Bn 图2 α-五角链的两种局部结构


图3 β-五角链Cn 图4 β-五角链的两种局部结构
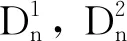

图5 γ-五角链Dn 图6 γ-五角链的两种局部结构
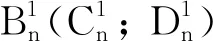


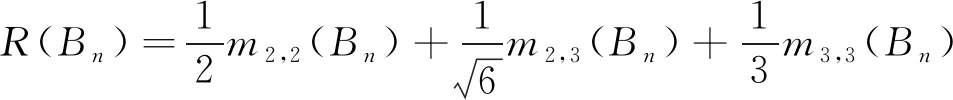
(1)

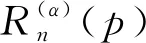
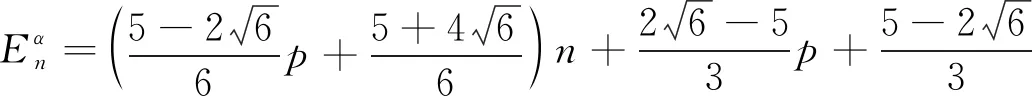
证当n=2时, 直接计算得
当n>2时, 显然m2,2(Bn),m2,3(Bn),m3,3(Bn)的值由图2中的两种结构确定.
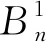
由(1)式得

(2)
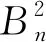
由(1)式得
(3)
结合(2),(3)式得
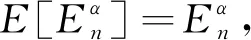
(4)
注意到(4)式为一阶常系数非齐次差分方程, 显然其所对应的齐次方程的通解为Eα=C, 这里C为常数. 设Eα′=kn为(4)式的一个特解, 将其代入(4)式可得
故(4)式的通解为
因此, 当n≥2时, 有
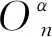
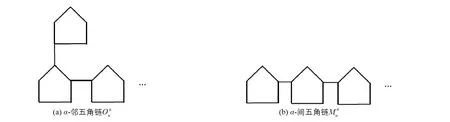
图7 α-邻五角链和α-间五角链
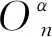
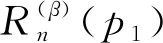
证证明方法与定理1完全相似, 不再赘述.

证证明方法与定理1完全相似, 不再赘述.

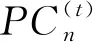
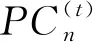
故由定理1、 定理2、 定理3分别可得下列定理4、 定理5、 定理6.
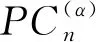

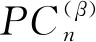
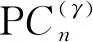
2 随机螺旋五角链的指标
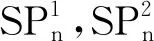
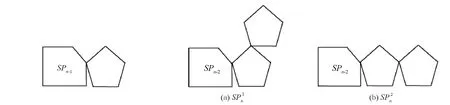
图8 螺旋五角链SPn 图9 螺旋五角链的两种局部结构
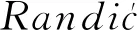
(5)

定理7设SPn(p3)是一个n长的随机螺旋五角链, 其中n≥2, 则
证当n=2时, 通过直接计算可得
当n>2时,m2,2(SPn),m2,4(SPn)及m4,4(SPn)的值可由图9中的两种结构来确定.
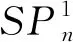
因此由(5)式得
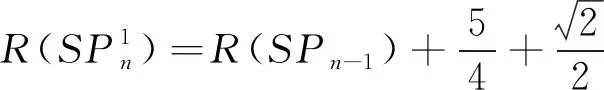
(6)
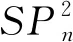
因此由(5)式得

(7)
结合(6),(7)两式得
又因E[En]=En, 应用期望算子可得

(8)
注意到(8)式为一阶常系数非齐次差分方程, 显然其所对应的齐次方程的通解为E=C1, 这里C1为常数. 令E′=sn是(8)式的一个特解, 将其代入(8)式可得
从而(8)式的通解为

故当n≥2时, 有
显然, 如图10所示的邻螺旋五角链On就是SPn(1), 而间螺旋五角链Mn就是SPn(0). 故由定理7得:

图10 邻螺旋五角链和间螺旋五角链