具有空变系数和吸收项的抛物方程解的爆破分析

欧阳柏平，蓝光进，郭斯维

（广州华商学院数据科学学院，广东 广州 511300）

1 引言

抛物方程解的爆破问题一直受到学者们广泛关注，并且取得了许多重要的研究成果[1-8]. 目前研究热点集中在含有时变或空变系数的抛物方程解的爆破[9-16]，特别是非局部的研究. 一般而言，抛物方程解的爆破问题主要依赖空间维数，初边值条件，局部或非局部以及非线性等.从理论和实用角度，对非局部的抛物方程解的爆破问题研究更有意义. 然而，一个突出的问题是局部的数学模型理论和方法不适合非局部的情况，需要重新构建新的理论和方法，因而会出现很多困难.

在齐次Dirichlet 和齐次Neumann 边界条件下，Song[14]研究了R3上一类半线性抛物方程解的爆破时间下界估计问题:

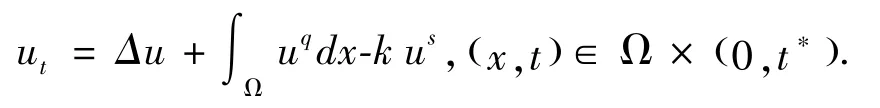
在齐次Dirichlet 和齐次Neumann 边界条件下， Song 和 Lv[15]研究了高维空间上具有加权项的抛物方程解的爆破率和爆破解的爆破时间上下界估计问题:

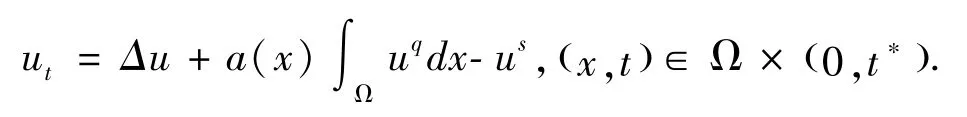
在Dirichlet 边界条件下，Shen 和Fang[16]研究了全空间上一类抛物方程解的非全局存在条件和爆破发生时解的爆破时间上下界估计问题:

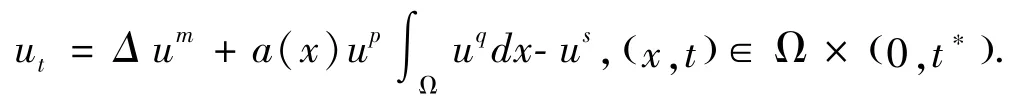
受以上文献的启发，本文进一步考虑如下更一般地非局部抛物方程解的爆破问题:

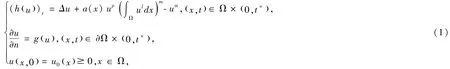
其中Ω 是Rn(n≥3) 中有界凸区域，其边界记为∂Ω，假设足够光滑. 当爆破发生时，爆破时间用t*表示.Δ 为拉普拉斯算子为u在∂Ω 上外法向量导数.

本文的目标是讨论Rn(n≥3) 上非线性边界条件下解的全局存在条件和爆破解的爆破时间上下界估计.为此，本文的主要困难在于找到恰当的能量泛函，妥善处理边界条件，高维空间以及方程中的非局部项和吸收项对解的爆破影响.

2 解的全局存在性

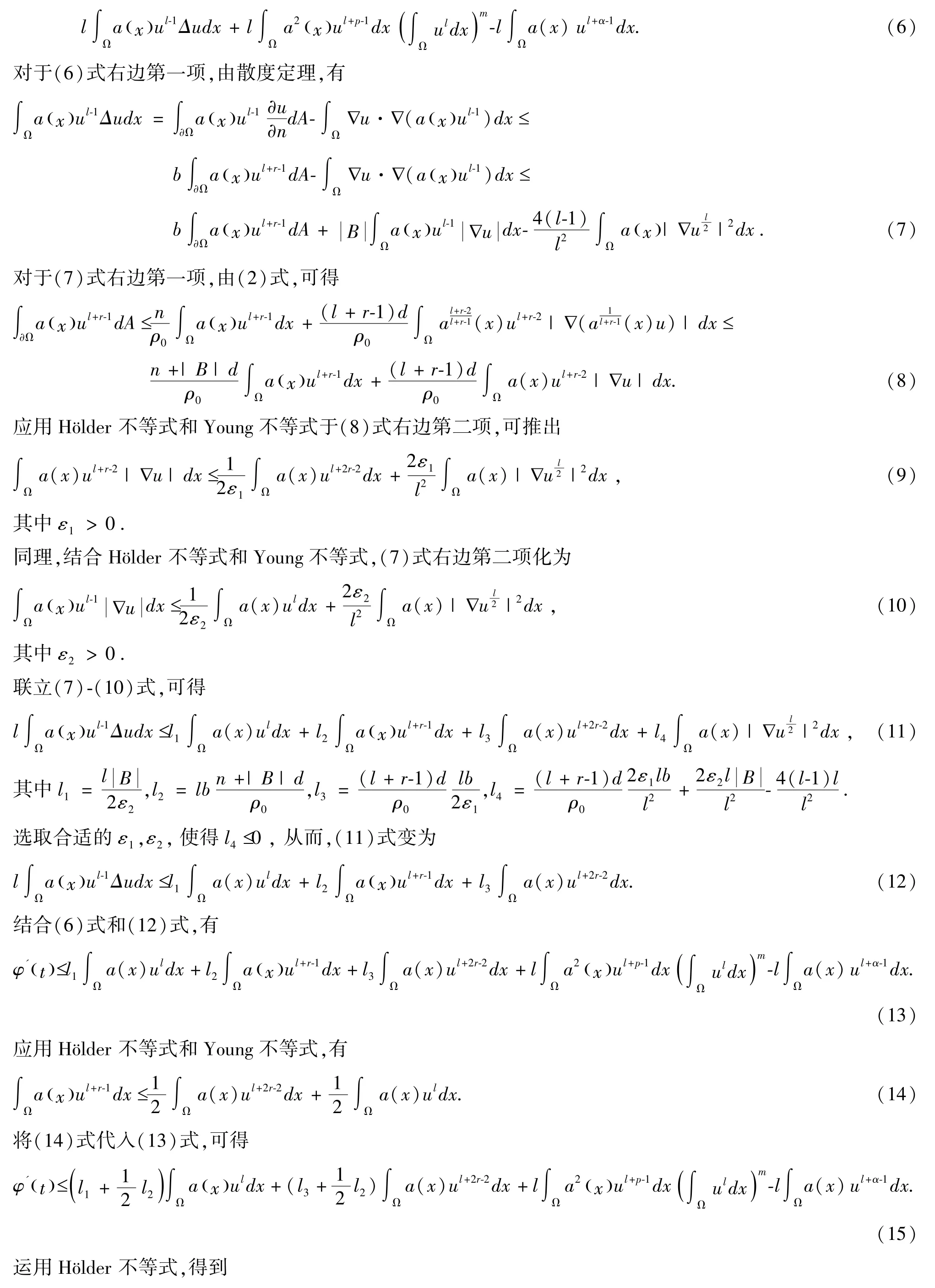
3 解的爆破时间上界估计

4 解的爆破时间下界估计