海底高压输油管道泄漏事故后果研究*

柴冲 侯磊 于巧燕 王瑞 李延豪 肖开喜

1中国石油大学（北京）机械与储运工程学院

2中国石油大学（北京）油气管道输送安全国家工程实验室

3国家管网集团北方管道公司

随着海洋油气工业的发展，海底管道里程呈爆发式增长。管道长期暴露在恶劣的海洋环境中，承受着复杂的工作载荷[1]。腐蚀、波流冲刷、海床运动、台风等均可能导致海底管道发生泄漏[2]。海底管道一旦发生泄漏，会大面积污染海洋环境，导致生态灾难。在具有剪切速度分布的海流作用下，油品到达海面的时间和向下游迁移的距离是指导维抢修快速反应的两个关键参数[3-4]。特别是对于生产平台或海岸附近的海底管道，一旦通过声波探测到溢油，几分钟内就可以实施快速救援[3]，因此应该研究油品在水下的扩散过程，预测溢油何时到达水体表面。

国内外学者提出多种模型，用于表征油品的迁移规律，李大鸣等[5-6]在水动力模型基础上建立海洋溢油模型，对有风和无风作用条件下的溢油扩散范围进行计算，发现油品垂直向上溢出时，水平迁移距离最小，且浮射流到达一定深度后，不会短时间到达水体表面；谢宁等[7]利用COMSOL 软件对比分析了泄漏孔径、泄漏速度与水流速度对成品油扩散的影响规律，发现泄漏孔径对最大扩散高度影响显著；王琪等[8-11]采用有限体积法，分析泄漏孔径、海水波动等对油品在水中的扩散轨迹的影响，发现海水波动会加剧水下溢油的离散化程度，使得水下溢油范围进一步扩大；李新宏等[12]基于CFD方法建立了海底油气管道泄漏事故后果的评估模型，对比分析了原油与天然气的泄漏扩散特性，发现原油的扩散轨迹对工况因素更加敏感；符泽第等[13-15]定量分析了不同工况下柴油在水中分布情况，发现孔径越小柴油越容易以滴液形式在水中扩散，孔径越大，泄漏量越大，扩散范围越大；YAPA[16-17]等基于Lagrangian 积分技术，建立了包含扩散、溶解与卷吸作用的溢油迁移扩散模型。以上研究对于管道泄漏速度边界条件的设置，多数研究者的取值集中在2～10 m/s[9-19]，这与高压输油管道的泄漏速度差别较大，且对泄漏孔位置对溢油扩散的影响研究较少有关。

为此，根据原油管道泄漏量公式[14]计算高压输油管道发生小孔泄漏后的油品泄漏速度，通过软件模拟辅助验证计算结果的准确性，通过咨询现场专家进一步确认了计算结果的准确性，最终确定管道在高压运行状态下发生小孔泄漏的边界条件；根据流体力学基本理论采用有限体积法（VOF），模拟不同泄漏速度、水流速度以及泄漏孔位置不同时溢油水体中的迁移扩散过程。

1 仿真模型的建立

1.1 物理模型

（1）二维模型。某海底输油管道敷设在水深为20 m 的海床表面，公称直径为813 mm，壁厚为11.7 mm，忽略油品沿管道轴向扩散，沿水流方向（管道径向）建立长度、深度分别为150 和20 m 的海底管道二维模型，底部圆形为管道横截面，海底输油管道泄漏计算模型如图1所示。

图1 海底输油管道泄漏物理模型Fig.1 Physical model of submarine oil transportation pipeline leakage

（2）边界条件。计算域左侧为水流入口，右侧为水流出口，泄漏孔位于管道表面，海水底部和管壁为壁面边界，海水上侧为自由表面。海风对溢油扩散距离的影响最终表现为海风对水流速度的影响进而带动溢油扩散，因此海流入口采用带有速度梯度的入口边界条件即可将风速对溢油扩散的影响包括在内。

根据入口速度随深度变化的关系[20]，水流入口速度公式为

式中：v为海水速度，m/s；vmax为水流最大速度，m/s。

出口边界条件采用压力出口，依据流体力学压力随深度变化关系[14]，出口压力公式为

式中：pout为水流出口压力，Pa；ρ为海水密度，kg/m3；g为重力加速度，9.8 m/s2。

根据液体管道泄漏量公式计算泄漏速度[14]，泄漏速度公式为

式中：Cd为泄漏系数，泄漏孔为圆形且雷诺数＞100，取0.6；A为泄漏孔的横截面积，m2；p1为泄漏源压力，Pa；pa为外部环境压力，Pa；H为泄漏点和压力源的高程差，m；pm为管道摩擦阻力，Pa；ρL为液体密度，kg/m。

设管道输量为1 200×104t/a，运行压力分别为1、2、3、5 MPa，管道泄漏孔尺寸为100 mm，经计算得关阀前泄漏速度分别为25、38、56、64 m/s。

（3）网格划分。蒋梅荣和李志刚[18]等根据FAN（1967）经典实验，选取了整体网格密度分别为0.05、0.10、0.15、0.20、0.25 m，溢油口加密网格尺寸为0.05 m，对不同工况下疏、密网格模型中溢油到达水体表面的时间进行对比分析。结果表明对于200 m×20 m的二维模型，网格稠密时，水下溢油形态与整个流场非常精细，且与FAN 实验吻合较好；随着网格尺寸的增大，模拟结果与FAN 实验值的吻合度逐渐下降，从对比情况来看，整体单元网格尺寸为0.2 m时满足计算精确度要求。

本研究模型的泄漏孔处网格尺寸为0.02 m，加密区域网格尺寸为0.1 m，整体网格尺寸分别为0.1、0.2、0.3、0.4 m，泄漏孔位置在管道正上方。泄漏速度为25 m/s时，溢油到达水体表面的时间以及到达水体表面时溢油的最大水平迁移距离见表1，溢油到达水面时的分布状态见图2。发现整体网格尺寸为在0.1 m和0.2 m时，油品到达水体表面的时间与最大迁移距离两参数接近，且符合FAN经典实验结果。整体网格尺寸控制在0.3 m和0.4 m时，油品到达水体表面的时间与最大迁移距离和前两种情况差别较大。为更加精细的描述出溢油在水下的分布，泄漏口网格尺寸取0.05 m，整体网格尺寸取0.1 m。

表1 不同网格尺寸时的油品水下运移参数Tab.1 Underwater migration parameters of oil under different grid sizes

图2 不同网格尺寸下溢油到达水面时的分布状态Fig.2 Distribution of leaking oil reaching to water surface under different grid sizes

1.2 数学模型

将原油和水均视为不可压缩黏性流体，在流体界面上，假设流体之间没有相变和滑移，流体流动控制方程包括连续性方程、动量方程、湍动能方程和湍能耗散率方程[19-20]。

连续性方程见公式（4）：

式中：ρi为流体密度，kg/m3；t为时间，s；u为矢量速度，m/s。

动量方程见公式（5）：

式中：ρ为流体密度，kg/m3；ui为i方向的速度分量，m/s；fi为i方向的单位质量力，m/s2；τ为黏性应力，Pa；p为流体微元的压力，Pa，xi、xj为空间位置。

湍动能方程见公式（6）：

式中：k为湍动能，取为常数1.0，m2/s2；Gk为平均速度梯度引起的湍动能产生项，kg/(m·s3)；μ为流体的动力黏性系数，kg/(m·s)；μt为流体的湍动黏性系数，kg/(m·s)；ε为湍动能耗散率，取为常数1.3，m2/s3；

湍能耗散率方程见公式（7）：

式中：σk为张力，N；C1ε、C2ε和Cμ为经验常数，分别取值为1.44、1.92、0.09。

溢油过程为瞬态过程，采用瞬态压力基求解器，多相流相界面追踪采用VOF 模型。为了保证计算精度，对流项和扩散项采用二阶迎风格式和中心差分格式。对于瞬态求解问题，PISO 算法相对于SIMPLE 算法，单个迭代步的收敛速度更快，总体效率更高，因此求解压力和速度耦合采用PISO算法[21]。湍流模型选取标准的k-ε模型，时间步长为0.01 s，Fluent软件模型参数设置如表2所示。

表2 FLUENT软件模型参数设置Tab.2 Parameter setting of Fluent model

2 结果与分析

2.1 泄漏孔位于管道上方

泄漏孔位于管道上方，泄漏速度分别为25、38、56 m/s，水流速度为1 m/s时，不同时刻的油水两相分布如图3所示。在导出模拟结果时，空气区域并未涉及溢油扩散，因此模拟结果仅展示了水体区域的溢油形态。溢油进入水体后，发生卷吸作用，根据LEE和CHEUNG[22]的研究，卷吸作用是指油流表面与水体之间相互作用，包括剪切卷吸和强迫卷吸。剪切卷吸是由溢油运动导致的油团与水环境之间产生的剪切应力引起的，强迫卷吸是在流动的水环境中水流进入油团内部引起的。油品在水中的运移状态可分为两个阶段：第一阶段油品在管道压力的作用下射入水体，油品以连续油流的形式在水中运动；第二阶段溢油初始动能减少，在水流的剪切作用下，连续的油流被冲散为液滴，在重力、浮力、惯性力和剪切应力的共同作用下继续运动。油品在大部分区域中都是以液滴或液滴组的形式出现。

图3 泄漏速度不同时的油品分布Fig.3 Distribution of oil under different leakage velocities

在泄漏开始的2 s 内，泄漏速度为25 m/s 时，油品向上运动的最大高度为7 m；泄漏5 s后溢油向上迁移至距离水底12 m 的高度；泄漏10 s 后溢油上浮至15 m；泄漏15 s后溢油到达水体表面。可以发现，泄漏后的5 s 内，由于具有较大的初速度，溢油向上运动较快；泄漏5 s 后，由于水体阻力作用竖直方向速度逐渐减小，油品只能在浮力作用下继续向上运动，因此向上的迁移速度显著减慢。当泄漏速度增加至56 m/s 时，在泄漏开始的2 s 内油品可迁移至距离水底15 m 的高度，3.5 s 后溢油到达水体表面。

泄漏速度由25 m/s增大至38 m/s时，溢油运动至水体表面的时间由15 s 缩短至5 s；泄漏速度增大至56 m/s时，溢油运动至水体表面的时间缩短至3.5 s；泄漏速度由56 m/s 逐步增大至64 m/s 时，溢油达到水体表面的时间基本不再变化，均只需3.5 s。可以得出：泄漏速度＜56 m/s时，溢油到达水体表面的时间随泄漏速度的增大而减小；泄漏速度＞56 m/s时，溢油到达水体表面的时间随泄漏速度的增大基本不再变化。这是由于当泄漏速度较小时，溢油的初始动能较小，溢油到达液面之前初始动能便减小至0，之后在浮力和水流剪切的作用下缓慢浮至水面，因此溢油到达水体表面所需时间较长；当初始速度较大时具有更大的上升动能，溢油可以直达水体表面，所需时间较短。此外，油品泄漏后沿水流向下游移动，海床附近水流速度小，油品的水平迁移距离较短；随着油品向上运动，水流速度增加，剪切作用增强，水平迁移距离明显增加。

2.2 泄漏孔位于管道侧方

2.2.1 水流速度的影响

泄漏孔位于管道侧方，泄漏速度为38 m/s，水流速度分别为1 m/s和2 m/s时，不同时刻油水两相分布如图4所示。油品在管道压力的作用下沿水平方向射出，泄漏的初始阶段油流沿海底运动，随着油流动能的减小，水流的剪切作用使连续的油流分散为液滴，在浮力作用与卷吸作用下上浮至水体表面。计算发现，首先到达水体表面的油滴并不是水平迁移距离最长的油滴。这是由于油滴在惯性力、浮力和剪切应力的共同作用下运动，从泄漏孔向水体表面扩散的过程中，首先到达水体表面的油滴受到较大的浮力，而水平迁移距离最长的油滴则受到较大水流剪切力，可以发现溢油在水下的迁移距离大于在水体表面的迁移距离。

图4 不同水流速度对油品分布的影响Fig.4 Effects of different water flow velocities on oil distribution

图5 为泄漏速度分别为25、38、56、64 m/s时，水流速度为1 m/s和2 m/s时，油品的水平迁移距离随时间的变化。从图5 可见，泄漏速度一定时，水流速度越大，油品的迁移距离越长。水流速度由1 m/s 增大到2 m/s，当泄漏速度为25 m/s 时，油品的水平迁移距离增加15.4%；当泄漏速度为64 m/s 时，油品的迁移距离仅增加5.2%。可以看出，泄漏速度越大，水流速度对溢油水平迁移距离影响越小。

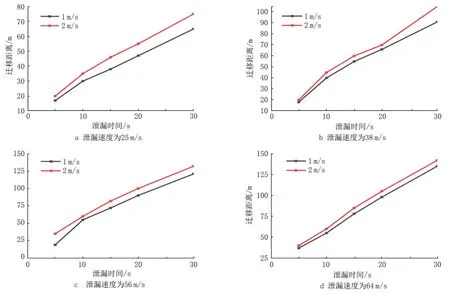
图5 泄漏速度改变时水流速度对溢油迁移距离的影响Fig.5 Influence of water flow velocity on oil spill migration distance when leakage velocity changes

2.2.2 泄漏速度的影响

不同泄漏速度下油品到达水体表面所需的时间以及该时刻油品在水中的最大水平迁移距离如表3所示。从表3可以看出，在不同泄漏速度下，油品到达水体表面所需的时间相近。

表3 不同工况下油品到达水体表面的时间及水平迁移距离Tab.3 Time of oil reaching water surface and horizontal migration distance under different working conditions

在相同的水流速度下，泄漏速度越大，到达液面时油品的的水平迁移距离越大。相同的泄漏速度下，水流速度越大，油流的水平迁移距离也越大。图6 是水流速度为1 m/s 时油品在水中的水平迁移距离随时间的变化曲线。由图6可见，不同的泄漏速度下油品迁移距离整体变化趋势一致，随时间的推移水平扩散距离逐渐增大。

图6 不同泄漏速度时油品迁移距离随时间的变化Fig.6 Change of oil migration distance with time at different leakage velocities

2.2.3 泄漏孔位置的影响

水流速度为1 m/s，泄漏孔位置由管道正上方变为管道侧方，不同泄漏速度时，溢油到达液面所需时间及水平迁移距离的变化情况见表4。泄漏速度为38 m/s时溢油到达水面的时间由5 s增加至34 s；到达水面时的水平迁移距离由14 m 增加至100 m，增长近7倍。泄漏速度为56 m/s时溢油到达水面的时间由3.5 s增加至30 s；到达水面时的水平迁移距离由12 m增加至120 m，增长10倍。因此相对于泄漏孔位于管道正上方，当管道侧方发生泄漏后，溢油在到达水面之前的水平迁移距离急剧增加，且泄漏速度越大，两种工况下水平迁移距离的差值越大。而水下污油的处理难度远大于水面污油的处理，因此在海底管道的侧方发生泄漏时对该片水域的污染程度更大。

表4 泄漏孔位置不同对溢油到达水面所需时间及迁移距离的影响Tab.4 Influence of different leakage hole positions on the time and migration distance of oil spill to water surface

3 结论

通过对海底管道泄漏的二维相场进行模拟，对比研究了水流速度、泄漏速度、泄漏孔位置对油品扩散的影响，依据计算结果得出以下结论：

（1）海底高压输油管道发生泄漏时，油品在迁移扩散至水体表面过程中，泄漏孔位置与泄漏速度对油品在水下的迁移轨迹影响大于水流速度对油品迁移扩散的影响。

（2）当泄漏孔位于管道正上方时，泄漏速度为油品上浮至水体表面所需时间的主要影响因素。当海水流速不变时，泄漏速度为25 m/s 增大至56 m/s时，油品到达水体表面由15 s缩短至3.5 s。

（3）当泄漏孔位于管道侧方时，溢油到达水体表面的时间不受泄漏速度和水流速度的影响，在不同泄漏工况下溢油到达水面的时间均为31～34 s。油品的水平迁移距离受泄漏速度的影响较大，水流速度为1 m/s 时，泄漏速度由25 m/s 增加至64 m/s时油品达到水体表面时，水平迁移距离由68 m 增加135 m，迁移距离增至原来的2倍。