基于磁流变阻尼器的建筑结构地震响应模糊控制
2022-04-20袁西贵
袁西贵
(成都职业技术学院,成都 610218)
0 引言
1948年,美国的Rabinow首先发表了有关磁流变液的磁流变效应,掀起了磁流变液及其装置的研究热潮。为减少地震对结构的影响,在建筑结构减震耗能领域,基于磁流变效应的磁流变液阻尼器因其诸多优点受到了人们的青睐。
如李宏男教授等[1]提出将MBC策略应用于隔震结构的半主动控制中。但磁流变液阻尼器参数难以建立精确的数学模型,模糊控制对其则是一种比较理想的控制方法。Bitaraf[2]利用模糊控制理论,对磁流变阻尼器实施控制,结果表明设计的模糊控制能够有效地降低系统的位移和加速度响应。
由于模糊规则一般是根据专家的知识和经验来决定,通过模糊推理求出控制量的大小。不同知识和经验设计的模糊控制有着不同的控制效果。文中则以磁流变阻尼器所在层的速度和位移响应为输入量,以电流为输出量,参考不同专家学者的成果,根据自己的知识和经验提出了相应的模糊规则。同时基于Simulink模块对比分析了有无模糊控制器两种情况下结构的地震响应,结果表明,基于文中提出的模糊规则及相关控制程序和分析方法用于MR阻尼器能够较好控制结构地震响应。
1 结构的运动方程
地震动作用下构件内力超过其强度时,构件发生破坏,为了减少地震对结构造成的破坏,可根据地震动和结构响应对结构施加主动控制或者控制力U(t),从而减少结构地震响应。一般在结构中安装耗能阻尼器,通过消耗地震能量达到减震的目的,如图1所示的布置方案。当地震发生时,由于楼层之间的相对位移,阻尼器就会产生相对运动,从而达到消耗地震能量,并起到保护主体结构的作用。
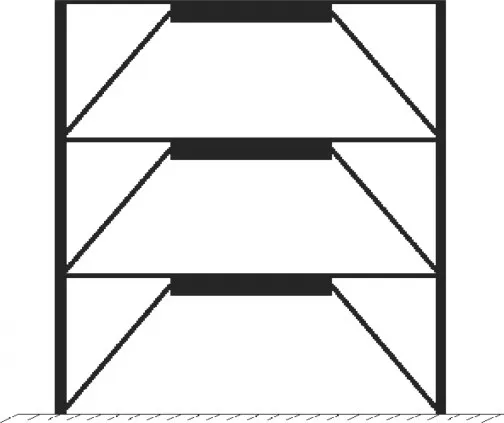
图1 水平安装阻尼器
在地震作用下,安装磁流变阻尼器结构的运动方程如下[3]:

式中,M、C、K分别为结构的n×n阶质量矩阵、阻尼矩阵及刚度矩阵;分别为结构的n×1阶相对层的加速度、速度和位移向量;则为地面地震加速度;F为外部作用矩阵(执行机构产生的控制力);I是n×1阶地震作用位置矩阵,为n×1维的单位列向量;F=BsU是n×1阶控制力向量;Bs是n×m阶控制器位置矩阵;U是m×1阶的控制力;m为控制器数目;n为建筑结构的楼层数。
结构的阻尼矩阵采用瑞利法计算得到:
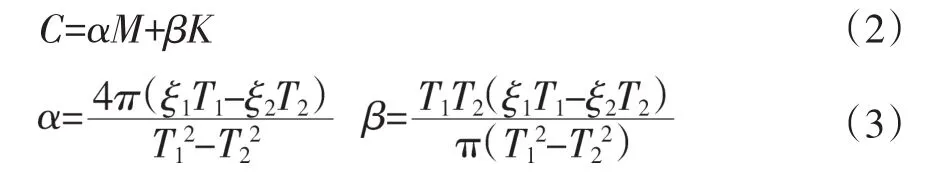
式中,ξ1和ξ2是结构的第一、二振型阻尼比;T1和T2是结构的第一、二振型的自振周期。
2 磁流变阻尼器模型
国内外学者对磁流变阻尼器的力学模型进行了大量的研究工作,并提出了多种力学模型,如Bouc-Wen模型、Bingham模型,还有改进的Bingham粘性弹性-塑性模型等[4-6]。文中采用Bingham模型,其应力应变关系:

对磁流变阻尼器,力与位移之间的关系还可以表达如下:
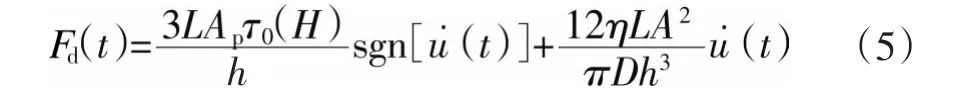
式中,L是活塞长度;D是缸体内径;h是孔道直径;AP是活塞有效面积。
τ0为屈服应力,与磁场强度有关,是控制电流的函数,屈服应力τ0和控制电流I的关系如式:

式中,A1=-11374,A2=14580,A3=1281;I为控制电流。
3 模糊控制器的设计
3.1 输入和输出变量论域
结构震动控制的目的就是使地震中的结构尽可能处于原平衡位置,因此,通常选择建筑结构在地震作用下结构的层间位移及层间速度作为模糊逻辑控制器的输入量[7-11]。调节磁流变阻尼器的控制力大小的电流则作为其输出量。也就是说磁流变阻尼器阻尼力的大小主要由结构的层间位移和层间速度共同决定。建筑抗震设计规范中将框架结构的弹性位移限值确定为层高H的1/550,弹塑性位移限值则为层高H的1/50,根据相关经验,结构位移反应基本论域可取层高H的0~1/200。磁流变阻尼器的输入电流,其基本论域可选在磁流变阻尼器的工作电流范围。
3.2 量化因子和比例因子
在使用计算机实现模糊控制算法以便进行模糊控制时,须将输入变量从基本论域转换到相应的模糊集论域。为实现实际的连续域到有限整数离散域的转换,需将输入变量乘以相应因子,这就是量化因子ke、kec及比例因子ku。
量化因子和比例因子都是在考虑两个论域变换基础上引出的,对输入变量而言的量化因子有量化效应,对输出变量来说比例因子仅起比例作用。量化因子的取值对控制系统的动态性能影响较大。当ke取值较大时,系统超调也较大,过渡过程也较长。kec取值较大时,超调量降低,但系统响应速度变缓慢。kec对超调的抑制作用相当明显。量化因子ke和kec的取值意味着对输入变量的误差及误差变化的不同加权程度,两者间相互影响。
3.3 模糊化处理
实际控制系统中输入量和输出量都是精确值,然而模糊逻辑控制器的输入和输出量确是模糊量,因此要把这一些精确量输入到模糊控制系统中去,就必须通过一定的规则将输入和输出精确量转换成模糊论域的模糊量,才能够通过模糊控制器进行结构的振动控制,这种把精确量转换成模糊量的过程便是模糊处理。所谓的模糊化就是根据需要把连续变化的模糊论域分成若干个等级,再将每个等级作为一个模糊变量,并对应一个模糊子集。一般模糊子集可用如下语言变量来描述:极小(ES)、小(S)、中(M)、大(B)、极大EB。常见的隶属函数有十余种,比如高斯隶属函数、三角隶属函数等。隶属函数分布形状对模糊控制性能也有很大影响,隶属函数的分布越集中,系统反应就越快,控制器对输入量的敏感性就越高,但其稳定性则要差一些;反之,系统的稳定性较好,但控制器对输入量的敏感程度降低。可由选取隶属函数应遵循的规则、各种隶属函数特性及相关经验,将位移、速度和MR阻尼器控制电流的隶属函数选为对响应比较灵敏的三角形隶属函数见图2、图3。
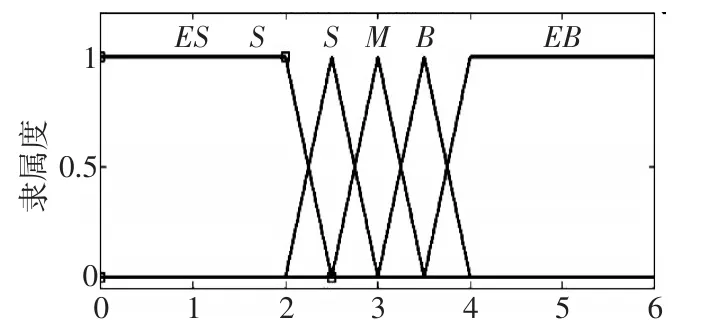
图2 位移(速度)模糊论域
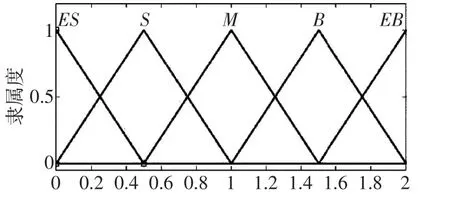
图3 电流模糊论域
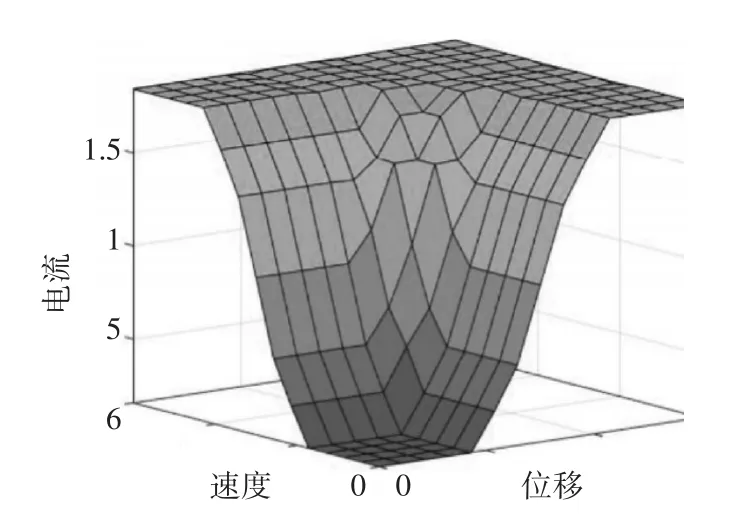
图4 模糊变量关系三维图
3.4 编写控制规则
模糊控制规则通常是源于专家知识和操作者的实际经验,通过将这一些知识和经验运用于实际工程中,并观察其控制结果,然后再总结经验,再应用于实际工程中,这样反复把理论知识和实践经验结合起来就总出符合实际情况的控制规则,并形成一个规则库。对土木工程结构来说,震动控制的目的就是要使得结构在地震作用下尽量保持在平衡位置,也就是让结构的势能随时处于最小。因此当结构发生位移偏离平衡位置且可能以较大速度达到最大位移之前,就应该给结构较大的反向力,让结构不要偏离平衡位置太大,这样就得到一条控制规则;当结构速度较小,位移也较小的时候,只需要给结构施加较小的反向力,这样就又得到一条控制规则,以此类推,可以得到其他规则,如表1所示。
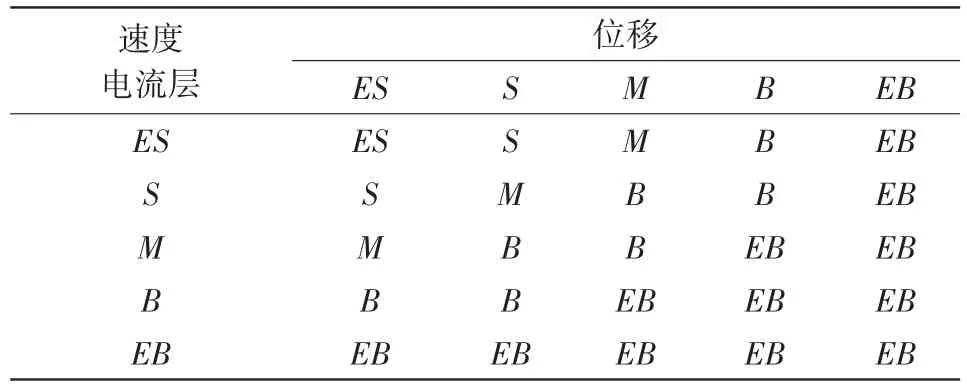
表1 模糊规则
4 算例分析
某4层框架结构的各层质量分别为m1=3.5×105kg,m2=m3=3.5×105kg;m4=3.1×105kg;m5=2.9×105kg;结构的各层刚度分别为k1=k2=k3=4.3×107,k4=3.6×107,k5=3.4×107,首层层高取4m,2~4层层高均取3.0m。阻尼器相关参数:活塞长度L取0.4m,缸体内径D设为0.1m,活塞的有效截面面积AP=6.6×10-3m2,活塞的阻尼孔直径D取2mm,磁流变体的动力粘度系数η=1.0,磁流变阻尼器的性能系数A1=-11374,A2=14580,A3=1281,第1~第4层阻尼器的安装数目分别为1、1、1、0;地震输入采用EL-Centro波,其幅值取为0.2g。结构阻尼矩阵可根据瑞利阻尼得到的由前两阶振型阻尼比确定,振型阻尼比取ξ1=0.05。
文中利用Simulink对地震作用下的无控和模糊控制器下的结构弹性响应进行了数值仿真分析,分析流程见图5、图6,计算结果见图7、图8。框架结构对EL-Centro地震波响应峰值及其控制率见表2。
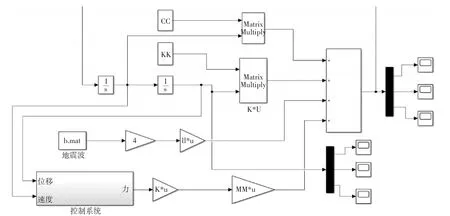
图5 模糊控制仿真图
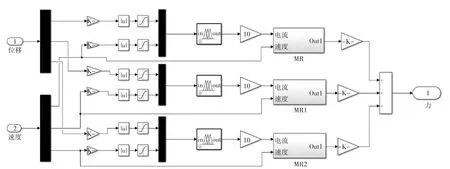
图6 控制系统
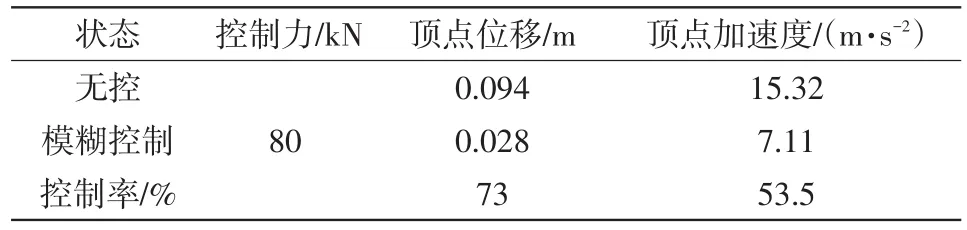
表2 结构地震响应峰值及其控制率
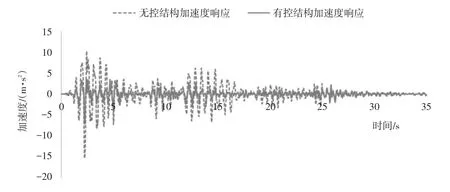
图7 顶层位移时程曲线
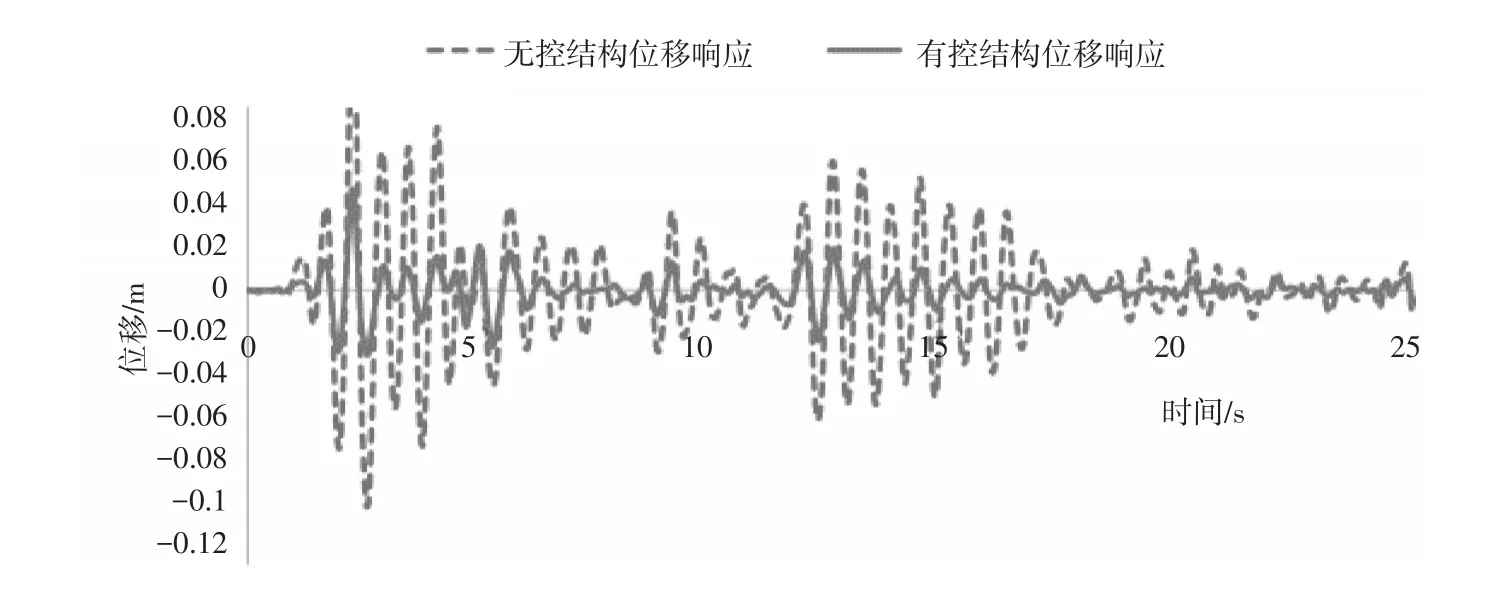
图8 顶层加速度时程曲线
从表2中可以看出,结构顶层的峰值位移在模糊控制下有了较明显的减小。在无控结构的顶层峰值位移为0.094m,而模糊控制结构的顶点峰值位移降为0.028m,减小了73%,无控时结构的顶点峰值加速度为15.32m/s2,模糊控制结构的顶点峰值加速度为7.11m/s2,减小了53.5%。
5 结语
文中通过对模糊控制器控制的建筑结构地震响应的研究,主要结论如下:
(1) 把层位移以及层速度作为模糊控制器的输入量对结构的位移和加速度响应均有较好的控制效果。
(2) 地震响应分析结果表明,设置模糊控制器的框架结构比无控框架结构的位移、加速度等地震响应都要小,其中对位移响应的控制率可高达73%,对加速度响应控制率也可达53.5%;由此可见,对安装MR阻尼器进行模糊控制有较好的减震效果。
